发展思维，发现数学的“真、善、美”

黄敏

[摘  要] 思维是数学生长的关键所在，在高中数学的课堂中，我们需要善于利用数学的魅力，挖掘其中的“真、善、美”，激发学生的思维，助推核心素养在高中数学学习中的渗透，促进学生核心素养的落地生根.

[关键词] 思维;核心素养;高中数学

发展学生的核心素养是当前教育界的热议话题，核心素养即是新课标的教学要求，也是时代发展所需的品质. 张殿宙先生说过，数学核心素养简单来说包括“真、善、美”三个维度，即体会数学的严谨、精确之“真”，学会用数学思想解决实际问题的“善”，欣赏数学智慧之“美”. 笔者多年从事高中数学教学工作，在实践与反思中逐渐领悟到数学思维是数学核心素养的灵魂，只有促使学生思维的发展才能真正践行数学核心素养的培养. 因此基于核心素养的高中数学教学要以培养学生的思维能力为主，本文结合实际就如何基于核心素养培养学生的思维谈谈作者自己的理解.

思维萌芽：基于“默会知识”展开问题

“默会知识”是一种经常使用却很难用完整形象的语言或者符号表示出来的知识，即我们常说的“只可意会不可言传”的知识. 虽然是隐性知识，但它却真实存在并且对思维的发展有着积极的作用. 在数学教学中，默会知识的存在往往标志着知识的起始，是思维的萌芽阶段.

例如：已知m2-mn-2n2=1，求m2+n2的最小值.

方法一：m2-mn-2n2≤m2+■am2+■-2n2=1+■m2+■-2n2.

令1+■=■-2，则a=■-3，

此时1+■=■-2=■.

所以m2-mn-2n2≤■（m2+n2），

即m2+n2≥■=■.

方法二：引入k，使得m2+n2-k（m2-mn-2n2）≥0恒成立，

即（1-k）m2+kmn+（1+2k）n2≥0.

令Δ=0，得k=■.

所以m2+n2≥■（m2-mn-2n2）=■.

方法三：令m2+n2=t=t（m2-mn-2n2），

所以（1-t）m2+tmn+（1+2t）n2=0，

所以1-t=0，m=±1，n=0

或1-t≠0，Δ=[t2-4（1-t）（1+2t）]n2≥0.

所以m2+n2≥■.

方法四：由已知得（m-2n）（m+n）=1，

可设m-2n=k，m+n=■，

所以m=■■+k，n=■■-k，

所以m2+n2=■2k2+■+2≥■.

由上述过程可见该问题有四种方法，方法一为待定均值法，方法二为待定配方法，方法三为判别式法，方法四为因式换元法. 在解决问题的过程中，学生常常会有“我怎么没想到这样做”的感觉，自己做的时候没有思路，而看了答案以后却恍然大悟，于是就会萌生“为什么能够想到这样做”的想法，其中的“为什么”就是默会知识的存在. 虽然默会知识很难用语言描述清楚，但数学中的默会知识常常倾向于解决问题的思路，因此教师在讲解问题时要将关注点至于问题的思路上，针对学生的实际需要展开问题，这样能够激发学生思维的萌芽，引导学生找到思维的方向，在解决问题的过程中发现数学的“真”，感悟数学的“善”.

思维可视：立足“出声思考”推进课堂

思维虽是一种心理活动，但它是可以描述的，课堂中思维的形成和发展过程最多的是体现在学生的学习活动中. 引导学生“出声思考”，大方展示自己的思维过程，让学习活动“发声”，这样思维就变得可听、可视，利于课堂的推进及思维的调整与发展.

以下是“对数（3）”的新授课中对换底公式的推导过程：

阅读下面一段内容：

设t=log35，则3t=5，对这个公式两边采用对数，得：lg3t=lg5？圯tlg3=lg5？圯t=■，即log35=■.

师：你从这个过程中发现了什么？

生1：我发现了一个底数可以转化成两个底数之商.

生2：我发现了等式左边对数的底数和真数经过转化都变成了真数.

师：你们都有着发现的眼光，你能否再举一例来佐证你的猜想呢？

生3：log47=t，则4t=7，两边取对数得lg4t=lg7，所以tlg4=lg7，所以t=■，即log47=■.

师：很好，你举的是和上述例子同类型的问题，那么我们对这个对数進行转换一定得转换成以10为底的对数吗？以别的底行不行呢？

生4：可以转换成任意大于0且不等于1的数作为底数. 如log47=■=■=■（a>0且a≠1）.

师：你研究问题真是细致，那你能否总结出更为一般性的结论呢？

生4：logab=■（a>0且a≠1，c>0且c≠1，b>0）.

师：你总结得真有研究，同学们是否也得出了同样的结论呢？

（众生均表示肯定）

师：同学们对于这个一般性的结论是否已经进行了证明呢？你的证明过程是怎样的？

生5：设logcb=M，logca=N，则b=cM，a=cN，所以logab=logcNcM=■logcc=■=■.

师：真棒，同学们已经具备了一定的自学能力，那么这个公式的作用是什么呢？

生6：将底数换成真数.

师：没错，这就是这个公式的重要作用，我们称之为换底公式.

在常态课中不难发现，高中数学课堂更多的是教师主导，学生习惯了专心听老师讲，而鲜有主动思考及师生交流的机会. 诚然，高中数学课因为教学容量较大，设置较多的师生互动环节在一定程度上会影响教学进度. 尽管这样，适当的师生交流也是必需的，在师生的交流过程中，学生的思维过程被一览无遗，通过师生的对话，教师可以获得学生最直接的思维过程，从而对其进行调整与完善，以引导学生正确的思维方向，构建完整的知识体系. 在思维调整的过程中，数学的严谨、完备得以体现，学生可以直接体悟数学的“真”.

思维聚焦：围绕“数学思想”提炼方法

高中数学的学习以掌握方法和发展能力为主要任务，以发展学生的数学素养为主要目标. 数学思想是数学思维的根基所在，在教学中注重数学思想的渗透是助推学生形成数学意识、发展数学能力、提高数学思维的重要途径. 因此在解决问题的教学过程中，对方法的提炼应围绕数学思想而展开.

以问题“已知实数a满足a≥1，且n=am+a2+2，求m2+n2的最小值”为例.

方法一：因为a≥1，所以a2+1≥2，所以m2+n2=m2+（am+a2+2）2=（1+a2）m2+2a（a2+2）m+（a2+2）2≥■=■=（a2+1）+■+2≥■. 当且仅当a=1时取等号.

方法二：由题意已知点（m，n）在直线ax-y+a2+2=0上，设原点（0，0）到这条直线的距离为d，则m2+n2≥d2=■2=■=（a2+1）+■+2≥■，当且仅当a=1时取等号.

上述解答过程中，方法一是消元法，将问题转化为以m为主元的二次函数，再利用二次函数的最值将其表示为含有a的代数式，进而解决问题，其中渗透了转化的思想. 方法二的主要思路是多元到一元的转化，其中蕴含了方程思想及数形结合思想. 在教学实践中会发现，学生的数学意识对思维的提高有着重要作用，数学意识就是我们通常所说的“数感”，而数感的形成离不开“推理、抽象、模型”等过程，同时也倚靠实践体验. 数学思想的渗透是将数学能力与数学方法聚焦于数学意识，促进数学意识的形成，同时解决问题的过程可以给学生最直接的实践体验，領悟数学方法之“美”，促进数学思维的提高.

思维发展：放眼“开放问题”，提升能力

随着时代的发展，当今社会对人才的创造能力与创新能力有着较高的要求，因此新课标对学生创造能力及创新能力培养也越来越重视，尤其对于即将踏入高等学府深造的高中生来说，这种能力是他们未来各方面能力综合发展所必需的. 能力的发展过程与思维的形成都是在学习中潜移默化而成的，并且它们是相互促进、相辅相成的. 对于高中数学教学而言，开放性问题的设置对学生思维的发展及创造力的形成有着非常显著的促进作用.

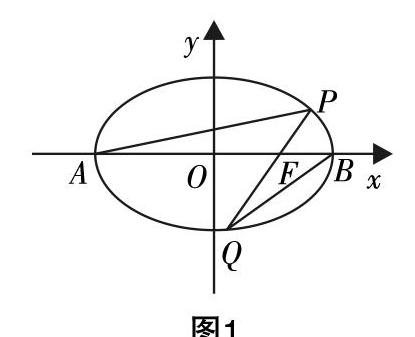
以章节复习课“椭圆”的教学设计为例，可以设置这样一道例题：

如图1，在平面直角坐标系中，已知椭圆C：■+■=1，点A，B分别为椭圆的左、右顶点，直线l过椭圆的右焦点F，并与椭圆交于P，Q两点，并且点P在x轴的上方.

（1）若FP=■FQ，求直线l的方程;

（2）你能否在题中再增加一个条件并自行编制一个问题进行解答呢？

（3）如果假设直线AP，BQ的斜率分别为k1，k2，是否存在一个常数λ，使得k1=λk2恒成立？如果不存在，请说明理由;如果存在，请求出对应的λ的值.

该例题包含三个问题，第一个问题为常规问题，是对基本知识的及时回忆及温故;第二个问题为全开放问题，学生可以在自己能力或稍高于自己能力的水平上编制适合自己的问题，使知识得到巩固的同时提高能力，同时学习小组间的相互交流，让问题进行传递，可以让学生相互促进、相互补充、共同进步，促进思维的发散;第三个问题为半开放问题，回答方式虽然不固定，但正确答案却是唯一的，需要学生在作出正确判断的同时对问题进行解答，该类问题的解答建立在完备的知识体系及正确的思维方向上. 开放性问题不仅有利于思维的发展与能力的提升，也便于教师分层教学与准确掌握学生的能力水平. 学生从自己编制问题及解决问题的过程中可以体会到解决数学问题的“美”，增强数感、提高思维.

高中数学核心素养包括数学抽象、逻辑推理、数学建模、直观想象、数学运算、数据分析这六个方面. 可见对于数学核心素养而言，数学思维是主线，更是主体，数学核心素养的形成都应建立在数学思维发展的基础上. 基于数学核心素养的思维培养应该始终以发展学生的数学核心素养为目标，以先进的心理学理论为指导，找到科学高效的培养方法. 数学是思维的体操，思维是数学的灵魂，对学生的数学思维培养的成效不仅在当下，更在未来，甚至可以让学生受用终生. 基于数学核心素养培养学生的思维能力，让学生发现数学的“真、善、美”，成为新时代的人才.