一个基于NTRU 的多密钥同态加密方案*

李瑞琪, 贾春福

1. 南开大学 网络空间安全学院, 天津300350

2. 天津市网络与数据安全技术重点实验室, 天津300350

1 引言

全同态加密(Fully Homomorphic Encryption, FHE) 是一种新型密码学工具, 其支持在加密信息上进行任意函数运算, 并且解密后得到的结果与在明文上执行相应运算的结果一致. 全同态加密的特性使其能够广泛应用于云计算、物联网等多种计算场景. 同态加密的思想最初由Rivest 等人[1]在1978 年提出(最初的概念被称作“privacy homomorphism”), 但在此之后一直都没有具体的构造方法, 直到2009 年Gentry 才构造出了第一个全同态加密方案[2,3]. 在Gentry 的开创性工作之后, 一系列关于全同态加密的研究成果相继出现[4-8].

多密钥全同态加密(Multi-Key Fully Homomorphic Encryption, MKFHE) 是FHE 在多用户场景下的一种推广, 其支持多方用户以各自的密钥对消息进行加密, 得到的密文可以一起参与运算, 运算结束后将各参与方的密钥收集起来得到联合密钥, 再用联合密钥对结果密文进行解密. MKFHE 在安全多方计算中有着重要应用. 当前有关MKFHE 方案构造的研究主要可以分为以下三类:

· 基于NTRU 方案. López 等首次提出了MKFHE 的概念,并且构造了第一个MKFHE 方案[8](下称LTV12 方案), 该方案是基于NTRU 加密体制[9,10]的. 作者利用重线性化(relinearization)和模交换(modulus switching) 技术获得一个层级多密钥全同态加密(leveled MKFHE) 方案.

· 基于Gentry-Sahai-Waters (GSW) 方案. 2015 年, Clear 等[11]构造了一个以GSW 方案[7,12]为基础的MKFHE 方案, 随后Mukherjee 等[13]对Clear 的方案进行了改进. 由于这两个方案需要在进行密文运算前就确定所有参与的用户, 因此这两个方案被称作单跳的(single-hop). 相对应地, Peikert 等[14]在2016 年提出了多跳的(multi-hop)MKFHE 方案(下称PS16 方案), 其支持运算得到的结果密文继续参与到接下来的计算中, 也支持新用户中途加入运算. 同年, Brakerski等[15]提出了与多跳类似的概念——全动态(fully dynamic), 并构造了一个全动态的MKFHE 方案(下称BP16 方案), 该方案支持任意用户在任意时刻加入运算. 多跳与全动态的区别仅在于是否需要在同态计算前输入参与运算的用户数的上限.

· 基于Brakerski-Gentry-Vaikuntanathan (BGV) 方案. 2017 年, Chen 等[16]提出了一个基于BGV[5]方案的MKFHE 方案(下称CZW17 方案). 该方案支持加密环中的元素而不只是1 比特, 并且该方案能够加入批处理机制.

上述三种类型的方案推动了MKFHE 的研究, 但仍然存在着一定的问题. 这些方案存在的最主要问题是, 参与运算的用户除了生成公私钥以及对消息进行加解密外, 还需产生大量额外的参数以保证多密钥的同态密文计算能够进行, 例如LTV12 方案、BP16 方案和CZW17 方案中需要用户生成运算密钥(evaluation key), PS16 方案则需要用户生成extension key 或冗余的密文, 这增加了用户端的计算开销.另外, 基于BGV 和基于GSW 的方案都需要进行密文扩张, 因为这两类方案中解密密钥的维数会随着用户数的增加而增加, 这使得密文的尺寸也要随之增加才能正确解密.

为了解决上述问题, 我们提出了一种新的多密钥同态加密方案, 利用工具向量和相应的分解函数将NTRU 方案转化成leveled MKFHE 方案. 本文所提方案的主要优势在于:

· 用户端只需要生成公钥和私钥以及对消息进行加解密, 并不需要生成evaluation key 或其他额外的参数, 减轻了用户端的计算负担.

· 使用比特分解技术来构造HE 方案,这使得密文加法和乘法能够简单地实现,不需要加入其它辅助技术(如relinearization);也使得NTRU 直接转化为leveled MKFHE 方案,从而不需要modulus switching 技术. 整个方案更加简洁、易于实现.

· 不需要进行密文扩张, 即密文的(最大) 尺寸是不变的.

· 支持加密环中的元素而并不只是1 比特, 因而本方案可以扩展成支持批处理的MKFHE 方案.

另外,我们的方案是一个leveled MKFHE 方案,仍需要利用Gentry 的bootstrapping 定理将leveled MKFHE 方案转化为一个完全的MKFHE 方案.

2 预备知识

本文中我们使用加粗大写字母表示矩阵, 如M; 使用加粗小写字母表示向量, 如v. 在矩阵中, M[i,j]表示位于第i 行第j 列的元素; 在向量中, v[i] 表示向量中的第i 个元素. 矩阵和向量中的元素标号从1开始. 本文中运算符“·” 表示矩阵乘法, 包括矩阵-矩阵乘法和标量-矩阵乘法(向量可以看作n×1 或者1×n 的矩阵).

其中δ 是一个只与环R 有关的常数, 称作环常数.

2.1 离散高斯分布

我们将均值为0、标准差为r 的离散高斯分布记作DZn,r. 在本文中唯一需要用到的有关离散高斯分布的性质是, 从DZn,r中抽取的样本的范数大概率在某一范围内. 由此我们可以定义如下的概念:

定义1[8]如果一族分布{χn}n∈N满足

则称其为B 界分布.

而离散高斯分布有如下性质:推论1[8]令R=Z[x]/〈φm(x)〉. 令χ 为R 上的B 界分布, 设f1,f2,··· ,fk←χ, 有

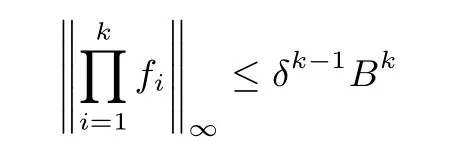
2.2 RLWE 问题与DSPR 假设

环上带错学习问题(Ring Learning With Errors, RLWE) 最初是由Lyubashevsky 等[17]提出的, 判别版本的RLWE 问题定义如下:

定义2[17]设U(X) 为集合X 上的均匀分布. 给定一个秘密多项式s ∈Rq, 一个R 上的分布χ, 我们定义一个Rq× Rq上的分布As,χ: 随机选取a ←U(Rq), 随机抽取一个差错e ←χ, 输出(a,b = a·s+e). 判别版本的RLWE 问题(记作DRLWEq,χ) 定义为: 当s ←U(Rq) 时, 区分As,χ与U(Rq×Rq) 两个分布.

下面的定理阐述了问题DRLWEq,χ的困难性, 即区分As,χ与U(Rq×Rq) 这两个分布是困难的.

2.3 多密钥同态加密

一个多密钥同态加密方案包含四个算法(KeyGen, Enc, Dec, Eval), 具体描述如下:

· (pk, sk)←KeyGen(1λ): 给定安全参数λ, 输出公钥pk 和私钥sk;

· c ←Enc(pk,m): 输入消息明文m 和公钥pk, 输出密文c;

· m:=Dec(sk1,sk2,···,skN,c): 输入密文c, 以及密文所对应的运算参与方的私钥sk1,sk2,···,skN,输出消息明文m;

· (c*,S) := Eval(C,(c1,S1),(c2,S2),··· ,(ct,St)): 算法的输入包括一个电路C, 以及t 个元组(ci,Si),i ∈{1,··· ,t}. 每个元组中包括一个密文ci和其对应的用户(密钥) 集合Si. 算法的输出为结果密文c*和其对应的用户(密钥) 集合S =∪Si(在用户(密钥) 集合中可以找到任意参与运算的用户的公私钥).

2.4 Bootstrapping

Gentry 在文献[2,3] 中提出了“bootstrapping” 技术, 该技术利用重加密的思想更新密文, 从而控制噪声膨胀以保证解密正确性, 进而实现任意次的密文同态运算. Gentry 的bootstrapping 定理也可以用于多密钥的场景. 具体来说, 该技术要求HE 方案能够对“增强解密电路(augmented decryption circuit)”进行处理, 同时也需要该HE 方案具有弱循环安全性(weakly circular secure). 有关bootstrapping 技术的更多细节参见文献[2,3].

定义4 令E 为一个多密钥同态加密方案. 该方案的增强解密电路fc1,c2定义为

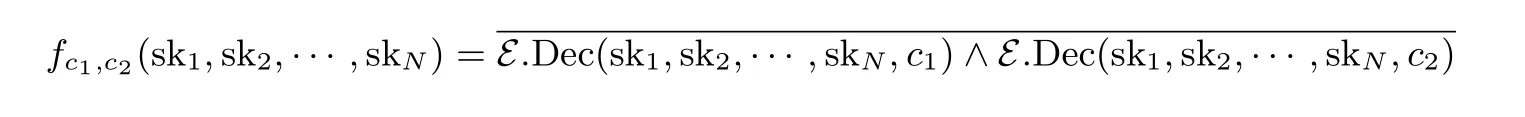
定义5 如果一个公钥加密方案在敌手获得其私钥的所有比特的密文时仍然是IND-CPA 安全的, 则称该方案具有弱循环安全性.

结合定义4 和5, 可以得到多密钥版本的bootstrapping 定理如下:

定理2 如果一个多密钥同态加密方案能够同态运行其增强解密电路, 并且具有弱循环安全性, 那么该方案就能转化为一个完全的多密钥全同态加密方案.

2.5 工具向量和比特分解函数

2.6 中国剩余定理与批处理

中国剩余定理(Chinese Remainder Theorem, CRT) 是一个重要的工具, 该定理内容如下:

定理3[23]设R 是一个环, I1,I2,··· ,Ik是R 中两两互素的理想, 于是有

每一个Zp[x]/fi(x) 可以看作一个“明文槽”, 利用该同构可以将k 个Fpd中的明文用Rp中的一个元素来表示, 并且有如下性质: 设(a0,a1,··· ,ak-1),(b0,b1,··· ,bk-1) ∈(Fpd)k是两组明文, 它们对应的Rp中的元素分别是a,b, 于是计算a+b 相当于计算(a0+b0,a1+b1,··· ,ak-1+bk-1), 计算ab 相当于计算(a0b0,a1b1,··· ,ak-1bk-1). 利用上述原理, 文献[24] 提出了支持SIMD (Single Instruction Multiple Data) 操作的HE 方案.

在此基础上, 文献[25] 利用Rp上的自同构映射a(x)a(xj) 并结合Beneš/Waksman 置换网络,可以使明文槽中的元素进行任意置换(permutation). 具体来说, 伽罗瓦群Gal(Q[x]/φm(x)) 中的元素为自同构映射xi,i ∈Z*m, 该伽罗瓦群包含了一个子群G ={xxpi|i=0,1,··· ,d-1}. 文献[25] 证明了商群H =Gal(Q[x]/φm(x))/G 可以使明文槽中存储的消息进行轮换(rotation). 因此, 以群H 所包含的自同构映射为基础再结合Beneš/Waksman 置换网络, 可以实现明文槽中元素的任意置换.

3 基于NTRU 的多密钥同态加密方案

3.1 NTRU 方案

我们首先介绍NTRU 方案, 这是构造我们的MKFHE 方案的基础.

给定安全参数λ, 设存在多项式时间的算法输出以下参数: 素数q =q(λ), 分圆多项式φm(x)(次数为n=n(λ)=φ(m)), B(λ) 界分布χ. 方案的明文空间为M=Rp, p 为小整数(例如2 或3), 方案所涉及到的所有运算均在环Rq=Zq[x]/〈φm(x)〉 中进行. NTRU 方案由以下三个算法组成:

· NTRU.KeyGen(1λ): 随机抽取多项式f′,g ←χ, 令f :=pf′+1. 如果f 在Rq中不可逆, 那么重新抽取f′. 输出公钥和私钥

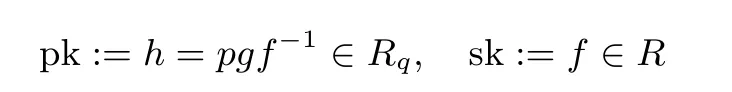
· NTRU.Enc(pk,μ): 随机抽取多项式s,e ←χ. 输出密文

· NTRU.Dec(sk,c): 计算μ′=f ·c ∈Rq, 输出

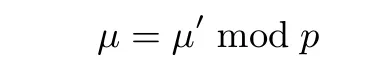
当‖fc‖∞≤q/2 时, 解密的结果是正确的, 这是由于此时fc mod q =fc.

3.2 基于NTRU 的多密钥同态加密方案

这一小节介绍我们的基于NTRU 的多密钥同态加密方案.

给定安全参数λ, 设存在多项式时间的算法, 输出素数q = q(λ), 分圆多项式φm(x)(次数为n =φ(m) = n(λ)), B(λ) 界分布χ. 设基为ω, ℓq=, 工具向量为g = (1,ω,ω2,··· ,ωℓq-1), 明文空间为M = Rp, 令p 为小整数且满足p ≤ω ＜q, 所有的运算均在Rq中进行. 我们的多密钥同态加密方案包括以下四个算法:

· MKHE.KeyGen(1λ): 调用NTRU.KeyGen(1λ), 输出公钥和私钥

· MKHE.Enc(pk,μ): 随机抽取ℓq组si,ei←χ 用于计算NTRU.Enc(h,0) 来得到ℓq个“0 的密文”, 然后将得到的ℓq个0 的密文组成一个向量c0∈, 最后输出密文

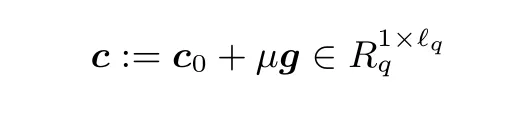
· MKHE.Dec(sk1,sk2,···,skN,c): 析取每个私钥ski得到ski= fi, 令联合私钥为sk := f =f1f2···fN. 计算并输出明文

· MKHE.Eval(C,(c1,S1),(c2,S2),···,(ct,St)): 设密文c1对应的用户(密钥) 集合为S1, 密文c2对应的用户(密钥) 集合为S2. 密文加法为

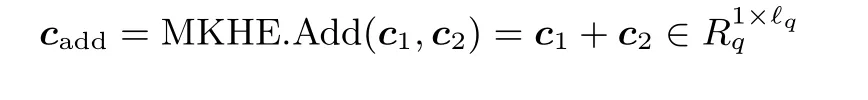
密文乘法为

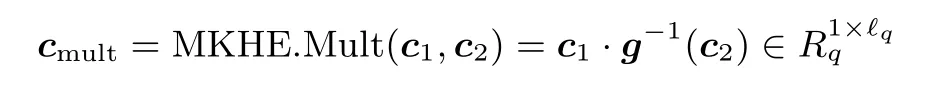
同时, 也需要输出cadd和cmult对应的用户(密钥) 集合S =S1∪S2.

4 方案分析

本节将对我们提出的MKFHE 方案的有关性质进行分析.

4.1 同态性分析

从而乘法正确.

在文献[8] 的最初构造中, 密文c2+需要使用联合私钥f2·解密, 而密文c+～c2需要使用联合私钥f ·解密, 也就是说联合私钥会随着运算电路的变化而变化. 但我们希望联合私钥仅与参与用户有关, 而与运算电路无关. 在文献[8] 中, 作者利用relinearization 技术解决了这个问题. 而在本文中, 我们的MKFHE 方案不需要额外添加任何技术就可以使得联合私钥只与参与用户有关, 不受运算电路的影响.下面我们来说明这一点.

事实上只需证明在本方案中, 仅使用私钥f 就能正确解密密文cmult=c·g-1(c) 即可.

与上文类似, 我们可将c·g-1(c) 表示为

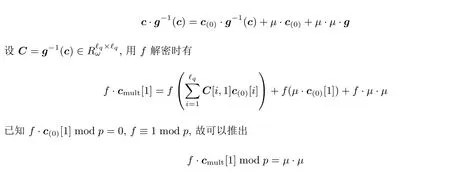
以上的推导说明了无论有多少个用同一公钥加密的密文相乘, 解密时只需使用原私钥, 这就意味着本方案中的联合私钥与运算电路无关.

4.2 安全性分析

4.3 噪声分析

在这一小节中, 我们将分析执行同态运算的过程中, 密文噪声的增长情况. 首先, 对密文的噪声进行定义:

定义6 设c 为一个密文, f 为其对应的私钥. 密文c 的噪声定义为

对于所有NTRU 类型的方案, 解密正确需要满足条件‖f ·c‖∞≤q/2. 因此在本方案中, 正确解密需要保证密文噪声满足noise(c)≤q/2.

下面的引理给出了执行一次同态运算后密文噪声的增长幅度.

引理3 令c,c′是两个密文, 它们对应的明文分别是μ,μ′, 对应的用户(密钥) 集合分别为S1,S2. 令c 和c′之间执行一次同态运算(加法或乘法) 后得到的密文所对应的用户(密钥) 集合为S =S1∪S2, 且S 中包含N 个用户(密钥). 解密cadd=c+c′和cmult=c·g-1(c′) 可以分别得到μ+μ′和μ·μ′. 如果noise(c)≤E,noise(c′)≤E, 那么进行一次同态运算后, 有noise(cadd),noise(cmult)＜(2pωnδB)2NE,参数p,ω,δ,n,B 的定义见3.2 节.

证明: 已知每个用户最初的私钥fi的范数上界为pB+1, fS=fi. 根据推论1 可知‖fS‖∞≤δN-1(pB+1)N＜δN-1(2pB)N. 对于加法有

本方案是一个leveled MKFHE 方案.

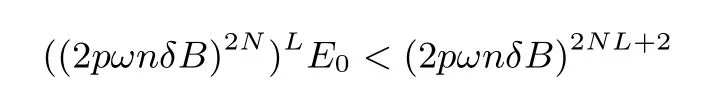
证明: 引理3 给出了一次同态运算后密文噪声的增长情况, 于是我们可以从初始密文中的噪声E0＜4p2δB2开始计算L 层(乘法) 运算后密文噪声的大小. 经过L 层运算后, 密文噪声增长为为了能够正确解密，我们需要保证(2pωnδB)2NL+2≤q/2. 已知p = O(1),ω = O(1),B = poly(n), 并且文献[3] 指出大多数情况下环常数δ 满足δ =poly(n)(这就要求我们选取满足此项要求的分圆多项式).根据上述条件可得

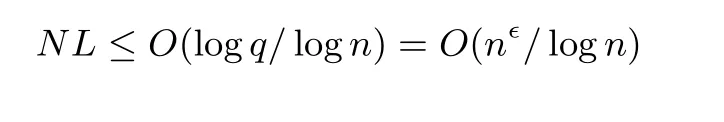
4.4 完全的多密钥全同态加密

上文中我们得到的方案是一个leveled MKFHE 方案. 在这一小节中我们将说明, 可以利用Gentry所提出的bootstrapping 定理, 将leveled MKFHE 方案转化为完全的MKFHE 方案.

Gentry 在其开创性的工作[2,3]中提出了bootstrapping 定理, 该定理指出如果一个同态加密方案能够同态运行自己的增强解密电路, 那么该方案就能够转化为一个完全的全同态加密方案. 因此, 需要对本方案的解密电路的深度进行衡量. 下面的引理给出了本方案解密电路深度的上界.

引理5 本方案的解密电路可以用GF(2) 上的深度为O(log N·(log log q+log n)) 的算术电路来实现.

证明: 假设c 是密文, 其对应的私钥集合为{f1,f2,··· ,fN}, 那么解密c 的过程可以表示为

文献[4] 已经证明, 两个Rq中的多项式的乘法可以通过深度为O(log log q+log n) 的布尔电路来实现. N 个多项式相乘可以通过深度为log N 的二叉树来实现, 因此解密过程的布尔电路的深度为

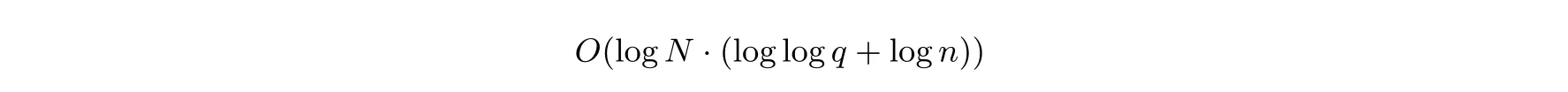
根据上文的结论, 我们得到定理5.

从而得到定理中的结论.

4.5 批处理

利用中国剩余定理和文献[24] 中提出的SIMD 技术, 可以将本方案转化为一个支持批处理的多密钥同态加密方案. 当选取合适的参数p 和分圆多项式时, 我们可以通过CRT 将一组明文(μ1,μ2,··· ,μk)映射为一个多项式μ=CRT(μ1,μ2,··· ,μk), 然后将μ 加密得到密文c. 根据同态加密和CRT 映射的特性, 并行加法和乘法可以分别通过密文加法和乘法实现. 因此在本小节中, 我们将主要讨论如何进行置换运算. 文献[25] 提出了以自同构映射为基础来实现置换的方法, 其中自同构映射是核心技术, 下文将介绍自同构映射在本方案中的应用.

设密文c 对应的明文为μ, 对应的密钥为f =f1f2···fN, 因此我们可知

其中e(x),k(x)∈R1×ℓq. 将自同构xxi,i ∈作用于该等式可得

已知φm(x) 能够整除φm(xi),i ∈, 从而我们可以将c(xi) 看作μ(xi) 关于密钥f(xi) 的密文. 然而我们需要的密文应当是对应于密钥f(x) 的密文, 因此我们在进行置换运算时, 需要借助于密钥交换技术(key switching), 将密文c(xi) 转化为一个新的密文c′= KeySwitch(c(xi)), 使得新密文能够用f(x) 解密. 下面将说明本方案中为实现置换运算所需要的密钥交换过程.

设密文c(x) 对应的联合密钥为f(x) = f1(x)f2(x)···fN(x), 密钥交换过程KeySwitch(c(xi)) 分为以下2 步:

· 拥有密钥fj的用户首先计算cfj= MKHE.Enc(hj,fj(xi)), 然后每个用户将各自的计算结果cfj发送到云端.

· 云端计算

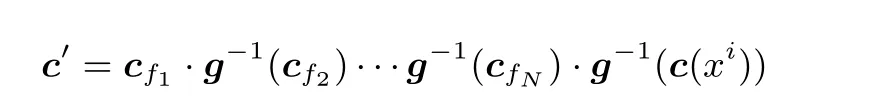
得到的计算结果c′即是所需的密文.

其中c(0),f1f2···fN是对应于密钥f =f1f2···fN的0 的密文. 显然, 当密文噪声不超过上界时, c′能够用f =f1f2···fN解密.

5 方案对比

本节中我们将对比本方案与其他经典方案在性能上的差异.

首先简要对比本方案与Doröz 等人[27]在2016 年提出的方案(下称DS16 方案) 之间的异同. 本方案与DS16 方案使用了类似的技术(即比特分解) 来处理噪声的增长, 但是不同之处在于DS16 方案使用了BitDecomp、Flatten 等函数进行比特分解; 本方案则利用工具向量g 及其相对应的分解函数g-1(·)进行分解, 此项差异造成了两个方案的密文大小以及同态运算的复杂度有所不同. 设n 表示分圆多项式的次数, q 表示模数, 那么DS16 方案中密文的尺寸为O(n log3q), 本方案中密文的尺寸为O(n log2q). 相较于DS16 方案, 本方案中的密文尺寸相对较小. 在同态运算过程中, DS16 方案需进行(维数为log q 的, 元素为多项式的) 矩阵加法和矩阵乘法, 本方案则进行的是(维数为log q 的, 元素为多项式的) 向量加法和矩阵-向量乘法. 相比之下, 本方案的计算复杂度较低. 另外, DS16 方案讨论的是单密钥场景下的同态加密算法, 不需要DSPR 假设; 而本方案是多密钥场景下的基于NTRU 的同态加密方案, 无法避免DSPR假设.

下面我们将与经典的多密钥同态加密方案进行对比.

5.1 与LTV12 方案的比较

本方案与LTV12 方案都是基于NTRU 的MKFHE 方案, 既有共同点也有不同点. 两个方案在噪声增长、可同态运行的电路深度等方面有着类似的结论, 但是二者是利用不同的技术达成的. LTV12 方案利用relinearization 技术消除了联合私钥中的平方项, 同时也实现了key switching 的功能; 又使用了modulus switching 技术, 将NTRU 方案转化为一个leveled MKFHE 方案. 这两项技术的使用使得LTV12 方案必须在生成公私钥的同时生成运算密钥, 并且在进行每一次同态运算(加法或乘法) 时都需要执行relinearization 操作, 每一层同态运算后都要进行modulus switching, 才能使得方案成为一个leveled MKFHE 方案. 而本方案使用了工具向量和比特分解技术, 使得实现同态运算所需的操作变得非常简单,不需要额外的技术,并且直接将NTRU 方案转化为一个leveled MKFHE 方案. 另外,实现本方案的同态运算过程仅需要普通的多项式加法和乘法, 以及一个将多项式分解的g-1(·) 函数. 相较于LTV12方案, 本方案更易于理解和代码实现.

表1 中列出了本方案与LTV12 方案的一些基本参数之间的对比, 其中n 表示分圆多项式的次数, q表示模数. 从表1 中可以看到, 我们的方案不需要运算密钥, 而LTV12 方案需要尺寸为O(n log3q) 的运算密钥. 虽然本方案在同态运算过程中的密文的尺寸是大于LTV12 方案的(表1 中密文尺寸一行), 但是运算后得到的最终密文(解密时所需的密文) 的尺寸与LTV12 方案相同(表1 中最终密文尺寸一行).

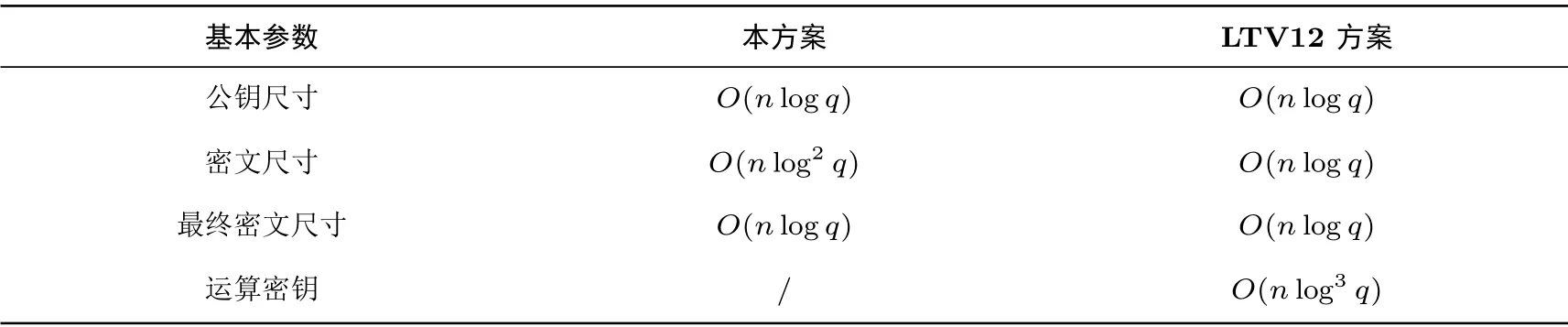
表1 与LTV12 方案的基本性质的比较Table 1 Comparisons of basic properties with LTV12 scheme

下面我们将对比本方案与LTV12 方案在云计算场景下, 用户端和云端分别所需执行的操作. 将同态加密算法应用于云计算场景时, 用户端需要执行的主要操作是生成密钥和同态计算所需的参数(即运行KeyGen算法), 加密(Enc) 和解密(Dec); 云端进行的操作则是对用户上传的密文进行同态运算. 我们对两个方案在用户端所需的操作进行比较, 因为在云计算场景中, 我们希望用户端的开销能够尽可能地降低. 比较结果如表2 所示.

我们将表2 中所列出的密钥生成和加密两个过程中用户端所做的操作综合起来进行对比: 若加密1 比特, 本方案中用户端所需的全部操作是随机生成2 个多项式, 进行log q 次多项式乘法和2 log q 次多项式加法; LTV12 方案中用户端所需的全部操作是随机生成2(log2q+log q) 个多项式, 进行6 log2q+1 次多项式乘法和8 log2q+2 次多项式加法. 由此可见, 当加密少量比特(例如对称加密算法的密钥) 时, 使用本方案在用户端的计算开销相对较低, 更符合云计算场景下用户的计算能力有限的特点.

表2 与LTV12 方案的基本操作的比较Table 2 Comparisons of basic operations with LTV12 scheme

5.2 与BP16、PS16 和CZW17 方案的比较

表3 中bootstrapping 一行表示, 每进行一次(门电路) 运算, 是否需要执行bootstrapping. PS16 方案中, 每执行一次与非门(NAND) 都要运行一次bootstrapping, 而其他方案并不需要. 从表3 中可以看出CZW17 方案需要生成evaluation key, 因而用户端的开销相对较大. PS16 中的两个方案虽然不需要evaluation key, 但是需要生成额外的密文或公共参数, 以保证多密钥同态运算能够正常进行. BP16 方案是当前理论上效果最佳的MKFHE 方案, 但是从表3 中可知, BP16 方案也需要生成evaluation key, 给用户端带来额外负担. 除此之外, 在BP16 方案中每执行一次NAND 运算, 都需要运行一次bootstrapping, 不易于代码实现; 而上文也提到过本方案的同态运算过程仅需要实现简单的多项式间的运算. 相较于BP16 方案, 本方案的同态运算过程更易于理解和代码实现.

表3 与其他MKFHE 方案的比较Table 3 Comparisons with other MKFHE schemes

6 总结

本文提出了一种NTRU 型的多密钥同态加密方案. 我们利用工具向量及相应的分解函数将NTRU方案转化为一个leveled MKFHE 方案, 并可以利用Gentry 的bootstrapping 定理将leveled FHE 方案转化为完全的FHE 方案. 由于使用了工具向量及分解函数, 我们的方案不需要使用relinearization 技术,从而不需要生成evaluation key. 与此同时, 本方案也不需要进行密文扩张以及生成额外的公共参数. 相比于已有的MKFHE 方案, 我们的方案更加简洁、易于实现, 并且在云计算环境下用户端的开销相对较小. 另外, 本方案支持加密环中的元素而不仅是1 比特, 因而也支持多密钥场景下的批处理同态运算. 本方案的安全性基于RLWE 问题和DSPR 假设, 而DSPR 假设并不是一个标准的密码学假设. 尽管到目前为止没有高效的方法去破解小模数情形的DSPR 假设, 我们仍可以认为DSPR 假设是安全的, 但是这个安全隐患需要引起关注. 当前, 基于NTRU 的MKFHE 方案无法避免DSPR 假设, 这是由解密时需要所有参与方的私钥相乘所造成的固有缺陷. 因此如何构造安全性只依赖于RLWE 问题的NTRU 型多密钥同态加密方案仍有待进一步研究.