基于双层加密的云存储数据去重方法*

高文静, 咸鹤群, 田呈亮, 李增鹏, 贺云龙

1. 青岛大学 计算机科学技术学院, 青岛266071

2. 中国科学院信息工程研究所信息安全国家重点实验室, 北京100093

1 引言

数据去重技术是一种高效的数据缩减技术, 可以有效的节省存储空间、降低传输带宽消耗. 数据去重也被称作重复数据删除(data deduplication), 即每个数据副本只在云服务器上存储一份, 并为拥有此数据所有权的用户创建访问链接[1]. 但随着云服务器端数据安全问题的不断出现[2], 为保护数据隐私, 用户普遍将数据进行加密后上传至云服务器存储. 对于云存储中加密数据的去重问题, Douceur 等人首次提出收敛加密(CE, convergent encryption)[3], 作为数据隐私性与去重高效性的平衡方案. CE 直接使用明文数据的哈希值作为加密密钥, 易于实现且计算效率高, 在云存储数据去重中得到了广泛的应用[4-6]. 但加密密钥过度依赖明文, 使其易遭受离线穷举攻击. 为明确安全目标, 定义形式化安全模型, Bellare 等人基于CE 提出了消息锁加密(MLE, message-locked encryption)[4], 加密密钥由明文数据和系统参数共同计算得到, 但本质上和收敛加密相同, 不能达到语义安全.

Puzio 等人提出ClouDedup 方案[5],在CE 的基础上,增加额外的加密操作和访问控制机制来保证数据的机密性. 该方案将数据外层加密和解密过程外包给第三方服务器, 并借助MM (metadata manager)来存储包括加密密钥在内的元数据. 该方案中系统要求额外服务器都是完全可信的, 且不能合谋. Stanek等人首次提出了“数据流行度” 的概念, 根据隐私程度将用户数据划分为流行数据和非流行数据[7]. 使用语义安全的加密算法保护非流行数据的安全, 对隐私程度不高的流行数据执行数据去重操作, 需借助完全可信的IS (indexing service) 提供索引服务. Puzio 等人提出PerfectDedup 方案[8], 通过完美哈希函数计算数据标识, 作为数据流行度查询的依据. 该方案需借助可信第三方保证非流行数据的语义安全, 实现对流行数据的去重. 但可信第三方在实际应用中部署困难, 易成为系统瓶颈[9].

Bellare 等人提出DupLESS 方案[1], 用户与密钥服务器KS (key server) 通过运行OPRF (oblivious pseudorandom function) 协议生成加密密钥, 保证数据的安全性. 该方案可有效的抵抗蛮力攻击, 同时也要求KS 完全可信, 难以抵抗KS 和云服务器的合谋攻击. Liu 等人提出一种无需可信第三方的加密数据安全去重方案[10]. 拥有相同数据副本的用户通过在线运行PAKE (password authenticated key exchange) 协议进行密钥交换, 能够有效的抵抗在线穷举攻击. 但该方案需要用户在上传数据之前, 与其他用户执行PAKE 协议来获取加密密钥, 要求参与协商的用户实时在线, 一定程度上增加了通信开销, 也降低了方案的实用性.

Stanek 等人在原有方案的基础上提出改进的门限数据去重方案[11], 其核心为门限密码系统, 进一步保证了非流行数据的语义安全. 该方案借助IRS (index repository service) 提供索引服务, 并进行流行度查询. 非流行数据采用双层加密, 在云服务器端仍保存多份副本, 存在较大的数据冗余. 该方案要求IRS完全可信, 才可实现数据的安全去重, 不能摆脱可信第三方的束缚. Yuan 等人提出dedupDUM 方案[12],支持用户动态管理, 采用预先验证的访问控制技术, 可验证用户身份的有效性. 该方案对用户数据采用重加密技术保护, 在随机收敛加密的基础上, 使用组密钥进行重加密. 组密钥根据组内用户信息生成, 每当用户组发生改变时, 组密钥都随之发生变化, 对用户数据进行一次重加密. 频繁的加解密操作一定程度上消耗了云服务器端的计算资源. Wang 等人提出一种基于密钥共享的数据安全去重方案[13], 对于收敛加密密钥的管理问题提出一种基于所有权证明的密钥共享方法, 但需借助可信第三方实现. Fan 等人提出了一种隐私保护的数据去重方案[14], 依赖可信执行环境TEE(trusted execution environment)提供安全的密钥管理, 可以有效的保护敏感数据的机密性.

针对以上问题, 本文提出了一种基于双层加密的云存储数据去重方案, 摆脱了可信第三方的束缚, 实现云存储中加密数据的高效去重. 主要贡献如下:

(1) 无需任何第三方参与, 加强了去重方案的实用性；

(2) 实现了对非流行数据的去重, 进一步提高去重效率；

(3) 添加了额外的安全机制, 有效防止非授权用户下载数据.

2 预备知识

2.1 收敛加密

收敛加密(CE, convergent encryption) 是解决加密数据去重的有效措施. 通过对明文数据M 进行哈希计算得到加密密钥K = H(M), 使用K 对M 加密得到密文C = SE(K,M). 收敛加密执行效率高, 但在数据的信息熵较低时, 易遭受离线穷举攻击. 即攻击者穷举{Mi}(i=1,2,···), 计算Mi的哈希值Ki=H(Mi), 并进一步计算密文Ci=SE(Ki,Mi). 通过对比C =Ci是否成立, 即可对明文数据M进行猜测.

2.2 ElGamal 公钥密码算法

ElGamal 公钥密码算法的安全性基于离散对数问题[15]. 设q 是一个大素数, G 为以g 为生成元的q阶循环群, 其中g ∈Zq.

离散对数问题: 若给定x, x ∈Zq, 计算y ≡gxmod q 是容易的; 但对于给定的y ∈G, 求解x ≡loggy mod q 是困难的. 我们把求解x ≡loggy mod q 的困难问题称为离散对数问题.

ElGamal 公钥密码算法主要包含以下三个函数:

(1) {pk,sk} ←KeyGen(q,G,g): 密钥生成函数, 以(q,G,g) 作为输入, 输出公私钥对{pk,sk}. 选取唯一的sk, 1 ＜sk ＜q-1, 计算pk=gskmod q. pk 为公钥, 对外公开; sk 为私钥, 由用户保存.

(2) c ←E(pk,m): 加密函数, 输入公钥pk 和待加密数据m, 输出密文c. 对于数据m, 首先选取一个秘密的随机数, 1 ＜k ＜q. 计算c1=gkmod q, c2=m(pk)kmod q. 输出密文c=c1‖c2.

(3) m ←D(sk,c): 解密函数, 输入私钥sk 和待解密密文c, 输出原始数据m. 其中c = c1‖ c2, 计算m=c2/c1sk.

2.3 所有权证明

所有权证明(PoW, proof of ownership)[16,17]是提高客户端数据去重方案安全性的有效措施. 通过执行PoW, 用户可以向服务器证明其确实拥有对某个文件的所有权, 而不是仅仅拥有文件的一小部分信息. Halevi 首次提出了基于Merkle hash tree (MHT) 的PoW 方法[17]. 用户端和服务器端都根据文件内容建立MHT, 并根据挑战问答的形式由服务器发起挑战. 用户端对给定叶子节点的子集提供有效的MHT 路径. 具体来说, PoW 是一种由证明者(用户) 和验证者(云服务器) 运行的交互式算法. 云服务器对于已存储的数据M, 计算关于M 的短信息值φ(M). 向云服务器证明对M 的所有权时, 用户计算并向云服务器发送φ′, 与其运行证明算法. 当φ′=φ(M) 并且证明正确时, 认为用户成功证明了对于M 的所有权.

2.4 双线性映射

设G, GT是2 个q 阶的乘法循环群, 其中q 为大素数, g 是群G 的生成元, 1GT是群GT的单位元.定义映射关系e:G×G →GT, 并满足在以下性质[18]:

(1) 双线性: ∀a,b ∈Zq, 都有e(ga,gb)=e(g,g)ab;

(2) 可计算性: ∀g1,g2∈G, e(g1,g2) 是可计算的;

(3) 非退化性: ∃g1,g2∈G, 使得e(g1,g2)／=1GT.

3 系统模型和定义

3.1 系统模型

本方案的系统模型如图1 所示, 包含云服务器和用户.

云服务器CSP (cloud service provider): 主要提供云存储服务, 用于存储用户数据. CSP 对存储的文件统计其合法上传用户并计数, 用于安全验证和文件流行度查询.

用户U (user): 将数据外包到云服务器以节省本地存储空间. 为保护数据隐私, 将数据加密后再上传至云服务器.

图1 系统模型Figure 1 System model

3.2 威胁模型

在本文方案中, 我们主要考虑以下两类攻击者:

(1) 内部攻击者: 指系统内部的敌手, 主要指云服务器. 我们认为云服务器是诚实且好奇的, 可对其存储的用户数据进行任意访问;

(2) 外部攻击者: 指系统外部的敌手, 主要指非授权用户. 外部敌手通过窃听公共信道获取部分上传数据的相关信息, 其主要目的是非法获取云服务器上存储的用户数据的明文信息.

3.3 安全目标

本文方案的安全目标如下:

(1) 数据的隐私性: 去重方案应保证存放在云服务器上用户数据的隐私性, 包括非流行数据和流行数据. 云服务不应获取任何关于其存储的用户数据的明文信息. 非授权用户不能获取关于云服务上存储的用户数据的明文信息.

(2) 数据的完整性: 去重方案应保证存储在云服务器上用户数据的完整性. 方案允许授权用户下载数据时验证其数据的完整性.

3.4 符号定义

本文中使用的符号如表1 所示.

3.5 函数定义

(1) KC←KGenCE(M), 收敛加密方案中的密钥生成函数. 输入数据M, 输出对应的收敛加密密钥KC.

(2) C ←Enc(K,M), 使用对称加密算法的加密函数. 输入密钥K 和待加密数据M, 输出加密后的密文C.

(3) M ←Dec(K,C), 使用对称加密算法的解密函数. 输入密钥K 和待解密数据C, 输出解密后的数据M.

(4) 安全的哈希函数H: {0,1}*→Zq; 短哈希函数SH: {0,1}*→{0,1}s.

(5) c ←E(pk,m), ElGamal 公钥密码算法中的加密函数. 输入公钥pk 和数据m, 输出密文c.

表1 符号定义Table 1 Symbol definition

(6) m ←D(sk,c), ElGamal 公钥密码算法中的解密函数. 输入私钥sk 和密文c, 输出原始数据m.

(7) K ←KeyExt(p,k), 密钥扩展函数. 输入辅助参数p 和初始密钥k, 确定性输出长度为l 的密钥.

(8) TF←TGen(p,CF), 标签生成函数. 输入参数p 和文件F 的收敛密文CF, 输出文件标签TF. 具体来说, 计算V = gH(CF)·p, Aux = gp, 数据标签TF为V 和Aux 组成的二元组, 即TF=＜V,Aux ＞. 本文方案中使用用户私钥sk 作为标签生成函数的参数.

(9) re ←TCheck(TF,Tag_List), 标签查找函数. 输入文件标签TF和标签列表Tag_List, 输出查找结果re. 若存在T′=＜V′,Aux′＞∈Tag_List 且e＜V,Aux′＞=e＜V′,Aux ＞, 则代表Tag_List 中已存在该文件标签, 输出re=T′; 否则, 输出re=0.

4 方案

本文提出一种基于双层加密的云存储数据去重方案, 无需第三方参与, 实现云存储中加密数据的高效去重. 通过划分数据流行度, 对隐私程度较高的非流行数据, 采用双层加密. 内层为简单高效的收敛加密,外层采用语义安全的对称加密. 加密密钥由用户根据数据信息结合云服务器提供的随机密钥计算得到, 不需借助额外服务器或实时在线用户传递密钥. 当云服务器上存储的用户数据达到流行度阈值时, 该数据转换为流行数据, 去除外层加密, 云服务器存储数据的收敛加密结果. 本方案能够实现对非流行数据的去重,而且在数据流行度转换时刻, 不需要用户重复上传数据, 进一步节省了网络带宽, 提高了去重效率.

方案主要包括三部分: 系统初始化, 文件上传和文件下载.

4.1 系统初始化

系统初始化阶段, 生成一个密钥池KeySet, 其中包含足够多数量的随机密钥, 密钥长度为固定值s.密钥池安全的存放在CSP 上. 对每一个加入系统的用户Ui确定唯一的身份标识IDi, 并为之分配专属的公私钥对{pki,ski}, 其中公钥pki对外公开, 私钥ski由Ui保存.

CSP 上存放有文件标签列表Tag_List,文件信息表DB.Tag_List 为CSP 上已存储数据对应标签的集合, 主要用于数据重复性检测. DB 与CSP 上存储的每一个文件相关联, 具体来说, 对于CSP 上存储的文件F, 以标签TF作为标识, 与其相关联的文件信息表DB[TF] 包含四条记录, DB[TF].data 为存储的文件密文, DB[TF].user 为文件的合法用户列表, DB[TF].rkey 为文件加密所需的随机密钥, DB[TF].ctr为文件的合法用户数量.

4.2 文件上传

用户Ui选择文件F 上传到云服务器CSP 存储时(文件上传的具体流程见算法1), 首先对F 进行收敛加密, 计算文件标签TF,i, 发送上传请求upload_request‖IDi‖TF,i到CSP. CSP 收到Ui的上传请求后, 进行数据重复性检测. CSP 运行标签查找函数re ←TCheck(TF,i,Tag_List), 若re = 0, 则本次上传为文件的初始上传, 执行算法2; 否则, 上传文件为重复文件, 且该文件在CSP 中对应标签TF为标签查找函数的返回值re, 执行算法3.

算法1 文件上传1. Ui:2. Compute convergent key KC ←KGenCE(F)3. Compute convergent ciphertext CF ←Enc(KC,F)4. Compute file tag TF,i ←TGen(ski,CF)5. Ui →CSP: Send upload_request ‖ IDi ‖ TF,i to CSP 6. CSP: re ←TCheck(TF,i,Tag_List)7. if re = 0, then execute Algorithm 2 8. else, TF = re, execute Algorithm 3

4.2.1 初始文件上传

上传文件F 为CSP 中不存在的文件时, 为初始文件上传.

CSP 首先将Ui上传的文件标签TF,i添加到文件标签列表Tag_List. Ui作为F 的初始上传者, 其上传的文件标签TF,i作为CSP 中对于F 的唯一标识, 即TF= TF,i. 其次初始化对应文件信息表, 设置DB[TF].ctr=0, 并在密钥池KeySet 中随机选取密钥rk, 令DB[TF].rkey=rk. CSP 将rk 用公钥加密RK ←E(pki,rk), 发送data_demand‖RK 到Ui, 要求Ui上传数据.

Ui收到RK 后用私钥对其解密rk ←D(ski,RK), 并以收敛加密密文的短哈希值SH(CF) 和rk 作为输入, 通过密钥扩展函数计算加密密钥K ←KeyExt(SH(CF),rk). Ui用K 对文件的收敛加密密文CF进行再加密得到双层加密密文←Enc(K,CF), 并将data_upload‖IDi‖发送到CSP.

CSP 收到Ui上传的数据后, 存储文件密文DB[TF].data =, 更新用户列表DB[TF].users ={IDi}, 并初始化DB[TF].ctr=1. Ui保存{TF,i,KC,K}.

至此, 文件上传结束. 初始文件上传的具体流程见算法2.

算法2 初始文件上传1. CSP: TF = TF,i, initialize DB[TF]2. DB[TF].ctr = 0 3. Select random key rk←RKeySet, DB[TF].rkey = rk 4. Encrypt rk using pki, RK ←E(pki,rk)5. CSP →Ui: Send data_demand ‖ RK to Ui 6. Ui:7. Decrypt RK, rk ←D(ski,RK)8. Compute encryption key K ←KeyExt(SH(CF),rk)9. Re-encrypt F, C*F ←Enc(K,CF)10. Ui →CSP: Send data_upload ‖ IDi ‖ C*F to CSP 11. CSP: DB[TF].data = C*F, DB[TF].users = {IDi}, DB[TF].ctr = 1 12. Ui: Store {TF,i,KC,K}.

4.2.2 后续文件上传

上传文件F 为CSP 中已存在的文件时, 为后续文件上传, 系统执行数据去重操作, 用户无需再上传数据.

CSP 发送PoWverif_request 给Ui, 要求进行PoW 验证. 若所有权验证通过, 则证明Ui确实拥有F, CSP 将对应文件信息表中信息进行更新, DB[TF].ctr+=1, 并将Ui添加到合法用户列表中DB[TF].users=DB[TF].users ∪{IDi}.

根据文件的合法用户数量DB[TF].ctr 和流行度阈值t 之间的关系, 又可分为以下三种情况:

(1) 当DB[TF].ctr ＜t 时, 我们定义F 为非流行文件, 具有较高的隐私性. Ui需与CSP 交互获取文件加密密钥.CSP 将文件随机密钥rk 用公钥加密RK ←E(pki,rk) 并发送给Ui. Ui收到RK 之后用私钥解密, rk ←D(ski,RK), 得到rk. 并计算文件加密密钥K ←KeyExt(SH(CF),rk). Ui保存{TF,i,KC,K}.

(2) 当DB[TF].ctr = t 时, 为流行度转换, 即经过本次上传之后, F 由非流行文件转变为流行文件.Ui需上传辅助信息, 用于存储在CSP 上文件密文的外层解密.CSP 发送auxinfo_demand 给Ui要求上传辅助信息. Ui计算辅助密钥auxKey=SH(CF) 并发送到CSP. CSP 计算加密密钥K ←KeyExt(auxKey,DB[TF].rkey). CSP 用该密钥解密已存储的文件密文←Dec(K,DB[TF].data), 并进一步验证SH() 与auxKey 是否相等. 若auxKey = SH(), 则解密正确, 并更新DB[TF].data =. 此时, CSP 上存储的数据为文件的收敛加密密文. Ui只需保存{TF,i,KC} 用于后期文件下载.

(3) 当DB[TF].ctr＞t 时,我们定义F 为流行文件,具有较低的隐私性. Ui只需自行保存{TF,i,KC},用于后期文件下载.至此, 文件上传操作结束. 后续文件上传的具体流程见算法3.

算法3 后续文件上传1. CSP →Ui: Send PoWverif_request to Ui 2. Ui running PoW with CSP 3. if verification successful, then 4. CSP: DB[TF].ctr+ =1, DB[TF].users = DB[TF].users ∪{IDi}5. if DB[TF].ctr ＜t, then 6. CSP: rk = DB[TF].rkey, RK ←E(pki,rk)7. CSP →Ui: Send RK to Ui 8. Ui:9. Decrypt RK, rk ←D(ski,RK)10. Compute encryption key K ←KeyExt(SH(CF),rk)11. Store {TF,i,KC,K}12. end 13. else if DB[TF].ctr = t, then 14. CSP →Ui: Send auxinfo_demand to Ui 15. Ui: Compute auxKey =SH(CF)16. Ui →CSP: Send auxinfo_upload ‖ auxKey to CSP 17. CSP:18. Compute encryption key K ←KeyExt(auxKey,DB[TF].rkey)19. Compute C′F ←Dec(K,DB[TF].data)20. DB[TF].data = C′F 21. Ui: Store {TF,i,KC}22. end 23. else, Ui: Store {TF,i,KC}24. end 25. else, return ERROR

4.3 文件下载

若用户Uj下载文件F, 则发送下载请求download_request ‖ IDj‖ TF,j到CSP. CSP 首先根据该用户上传的文件标签TF,j查找CSP 上F 对应的文件标签TF. 其次, CSP 查询用户权限, 若IDj∈DB[TF].users, 则为合法用户, 进一步验证用户身份. CSP 选取随机数r, 用该用户的公钥加密R ←E(pkj,r) 并发送给Uj. Uj用私钥解密得到r′←D(skj,R), 将H(r′) 发送给CSP. CSP 计算H(r)并与收到的H(r′)对比,若H(r′)=H(r),则用户身份验证通过,CSP 发送密文C =DB[TF].data给Uj.

Uj收到文件密文后, 对密文进行解密, 分以下两种情况:

(1) Uj保存有{TF,i,KC,K}, 则首先计算MF←Dec(K,C) 并进行验证. 若TGen(skj,MF) =TF,j, 则MF为F 的收敛加密密文, 进一步用收敛加密密钥KC进行解密得到原始文件F =Dec(KC,MF). 若TGen(skj,C)=TF,j, 则CSP 上存储的F 已转变为流行文件, 此时Uj收到的文件密文为收敛加密密文,直接用收敛加密密钥KC进行解密得到原始文件F =Dec(KC,C).否则, 返回错误信息.

(2) Uj保存有{TF,j,KC}, 首先进行验证, 若TGen(skj,C) = TF,j, 则确定C 为F 的收敛加密密文, Uj用收敛加密密钥进行解密得到原始文件F =Dec(KC,C).

文件下载的具体流程见算法4.

算法4 文件下载1. Uj →CSP: Send download_request ‖ IDj ‖ TF,j to CSP 2. CSP: TF ←TCheck(TF,j,Tag_List), check whether IDj ∈DB[TF].users or not 3. if IDj ∈DB[TF].users, then 4. CSP: Select random number r, compute R ←E(pkj,r) and send R to Uj 5. Uj: Compute r′ ←D(skj,R), and send H(r′) to CSP 6. CSP: Check whether H(r′) = H(r)7. if H(r′) = H(r), CSP send C = DB[TF].data to Uj 8. Uj:9. if have {TF,i,KC,K}, then 10. Compute MF ←Dec(K,C)11. if TGen(skj,MF) = TF,j, then compute F = Dec(KC,MF)12. else if TGen(skj,C) = TF,j, then compute F = Dec(KC,C)13. else, return ERROR 14. end 15. else if have {TF,j,KC}, then 16. if TGen(skj,C) = TF,j, then compute F = Dec(KC,C)17. else, return ERROR 18. end 19. end 20. else, return ERROR

5 安全性分析

根据3.2 节提出的威胁模型, 本文方案主要考虑来自内部敌手和外部敌手的攻击. 内部敌手主要指云服务器, 外部敌手主要指非授权用户. 本文提出方案中涉及的系统参数及3.4 节定义的函数均对外公开.我们认为CSP 是诚实且好奇的, 非授权用户可能会通过假冒合法用户与CSP 进行交互, 尝试对CSP 上存储的用户数据进行非法访问. 我们假设外部敌手凭借其攻击能力, 可窃听公共信道获取部分上传数据,从而对用户数据进行蛮力攻击.

5.1 数据标签的安全性

本文方案中由用户计算数据标签, 云服务器基于双线性映射e 检测数据重复性. 方案应保证数据标签的安全性, 接下来从数据标签的正确性、数据标签的唯一性和抗穷举攻击三方面进行分析与证明.

5.1.1 数据标签的正确性

定理1 文件F 的初始上传者Ui计算文件标签TF,i=＜Vi,Auxi＞, 上传到云服务器中保存, 作为F 的唯一标识. 那么, F 的后续上传者Uj计算文件标签TF,j=＜Vj,Auxj＞, 一定满足e(Vi,Auxj) =e(Vj,Auxi).

证明: 根据标签生成函数, Vi= gH(CF)·ski, Auxi= gski, Vj= gH(CF)·skj, Auxj= gskj, 其中CF为F 对应收敛密文. 由双线性映射的性质, 可得以下等式:

不失一般性, 不同用户Ui和Uj对相同文件F 计算的文件标签TF,i=＜Vi,Auxi＞, TF,j=＜Vj,Auxj＞,一定满足e(Vi,Auxj)=e(Vj,Auxi). 由此可证数据标签的正确性.

5.1.2 数据标签的唯一性

引理1 (哈希函数的抗碰撞性) 对于安全的哈希函数H : {0,1}*→Zq, ∀M1,M2∈{0,1}*, 且M1／= M2, 使得H(M1) = H(M2) 的概率是可忽略的. 我们用ε 表示可忽略值, 即: Pr[H(M1) =H(M2)|M1／=M2]≤ε.

定理2 设文件F 的初始上传者Ui计算文件标签TF,i=＜Vi,Auxi＞, 上传到云服务器中保存, 作为F 的唯一标识. 当用户Uj上传文件F′时, 计算文件标签TF′,j=＜Vj,Auxj＞, 上传到云服务器进行数据重复性检测. 方案保证数据标签的唯一性, 即存在F ／= F′, 使得e(Vi,Auxj) = e(Vj,Auxi) 的概率是可忽略的:

证明: 采用反证法进行证明. 假设存在F ／=F′, 使得e(Vi,Auxj)=e(Vj,Auxi). 即

当F ／= F′, CF／= CF′. 根据引理1, Pr[H(CF) = H(CF′)|CF／= CF′] ≤ε. 不失一般性, 若e(Vi,Auxj)=e(Vj,Auxi), 则H(CF)=H(CF′), 与假设相矛盾, 所以假设不成立. 即当且仅当F =F′时, 才满足e(Vi,Auxj)=e(Vj,Auxi). 由此可证数据标签的唯一性.

5.1.3 抵抗穷举攻击

本节针对方案中数据标签存在被穷举攻击的风险进行安全性分析. 假设存在一个多项式时间的敌手A, 针对某一文件的标签TF=＜V,Aux ＞进行离线穷举攻击, 进而猜测TF对应的数据明文M. 攻击过程如下:

①A 穷举数据{M′}, 对其进行收敛加密得到收敛加密密文CM′;

②A 选择随机数r←RZq, 运行标签生成函数TM′←TGen(r,CM′), 得到TM′=＜VA,AuxA＞, 其中VA=gH(CM′)·r, AuxA=gr;

③A 通过标签查找函数中的匹配算法，对比e(V,AuxA) 与e(VA,Aux) 是否相等;

④若e(V,AuxA)=e(VA,Aux), 则A 猜测TF对应的数据明文M =M′.

在明文空间足够大的情况下, A 不知数据大小|M|, 以上攻击是不可行的. 在实际应用中，用户外包到云服务器存储的数据小到几 KB, 大到数 GB (例如视频文件). 假设明文空间 MS ={M|M ∈{0,1}*,|M|≤n}, n ＞230×8. A 在该明文空间下穷举数据M′∈MS, 成功攻破标签TF的概率远远小于, 我们认为此概率是可忽略的.

5.2 保证数据的隐私性

方案保证存储在CSP 上用户数据的隐私性, 敌手不应获取任何数据明文.

定理3 本文方案可防止CSP 获取其存储的用户数据明文.

证明: 尽管CSP 可获取用户数据密文, 根据存储的文件信息表, 可获取文件的流行度和随机密钥,但仍不能解密得到数据明文. 对于某个特定密文C, 若为非流行数据的密文, 为双层加密密文. 内层为收敛加密, 外层采用语义安全的加密算法保护, CSP 在没有密钥的情况下难以解密. 即使C 为流行数据的收敛加密密文, 根据引理1, CSP 在不知明文M 的情况下, 难以计算出收敛加密密钥H(M), 不能对C 进行解密. 即CSP 无法解密获取用户数据明文.

引理2 (公钥密码的安全性) 基于离散对数困难问题的ElGamal 公钥密钥体制是安全的, 即在没有私钥的情况下, 成功解密经公钥加密的密文的概率是可忽略的.

定理4 本文方案可有效的阻止非授权用户获取用户数据明文.

证明: 非授权用户Ua想要获取CSP 上存储的数据, 根据4.3 节中的文件下载操作流程, 可能假冒合法用户身份并使用其身份标识IDi, 发送download_request‖IDi‖TF,i到CSP, 通过权限验证. CSP发送使用公钥pki加密的随机数密文R = E(pki,r), 根据引理2, Ua在没有私钥的情况下, 无法解密获取r. Ua不能返回给CSP 正确的验证信息, 难以通过身份验证. 即非授权用户Ua无法获取CSP 上存储的数据.

5.3 允许授权用户验证数据的完整性

定理5 CSP 上存储数据的可验证性. 授权用户可通过下载数据并检测标签的一致性, 验证存储在CSP 上数据的完整性.

证明: 由4.3 节中文件下载部分, 授权用户Ub请求下载文件F, 通过CSP 发起的用户身份验证之后, 收到由CSP 发送的密文C. Ub对密文进行解密的过程中即可验证数据完整性.

5.4 能有效的抵抗蛮力攻击

本文方案考虑外部敌手对CSP 上存储密文发动蛮力攻击的情况, 本节主要针对该攻击, 进行安全性分析, 建立一个安全模型游戏Game. 在该游戏中, 除了云服务器和用户, 同时还存在一个多项式时间的攻击者A. 假设在游戏的交互中, A 凭借其攻击能力, 获取了存储在CSP 上的密文C. 本文方案能有效的抵抗来自A 的蛮力攻击.

引理3 (蛮力攻击) 收敛加密的密钥由原始文件计算得到, 密钥过度依赖明文. 若敌手已知密文, 便可穷举数据, 对其进行加密并与已知密文进行对比, 则可能猜测出原始数据.

定理6 CSP 上存储密文的不可区分性可保证去重方案能有效的抵抗蛮力攻击. 即A 已知存储在CSP 上的密文C, 通过暴力穷举的方式猜测出原始数据M, 赢得游戏Game 的概率是可忽略的.

5.5 进一步讨论

5.5.1 使用短哈希函数SH 的原因

本文方案中使用短哈希函数SH: {0,1}*→{0,1}s计算收敛加密密文的短哈希值SH(CF), 作为计算数据外层加密密钥的辅助参数. 方案中使用短哈希函数主要有以下两个原因:

(1) 在4.2.2 节中, 后续文件上传的流行度转换情况, 上传用户需计算辅助密钥auxKey = SH(CF)并发送给CSP, 用于CSP 计算数据外层加密密钥. 由于短哈希函数会增加碰撞率, 不同的数据可能计算出相同的短哈希值. 所以即使在传输过程中, SH(CF) 意外泄露了, 敌手也无法从其中获取关于原始文件F 的有用信息.

(2) 短哈希值长度更短, 计算或传输的效率更高, 减轻用户端计算负担.

5.5.2 方案的改进

为了节省网络带宽, 本文方案仅要求文件的初始上传者上传文件数据, 后续上传者只需进行验证而不需上传数据, 极大的节省了用户和云服务器间的通信开销. 而且, 本文方案具有更高的灵活性, 若用户存在较高的安全性需求, 本文方案只需很小的代价就可改进为服务器端数据去重, 能够有效的抵抗侧信道攻击[21], 从而具有更高的安全性.

具体来说, CSP 在用户请求上传文件时, 无论该用户是否为文件的初始上传者, 均要求用户上传数据密文. 即在4.2.2 节中, 对于后续文件的上传, CSP 发送data_demand 给用户, 要求用户上传密文. CSP收到用户上传的密文后, 再执行去重操作. 该改进方案基于服务器端去重, 在一定程度上会增加网络带宽消耗, 但具有更高的安全性.

6 仿真实验

我们分别模拟实现了云服务器端和用户端. 使用一台戴尔OptiPlex 5250 台式计算机模拟云服务器,配备有3.20 GHz Intel(R) Core(TM) i5-6500 四核处理器和8 GB 运行内存, 运行操作系统为Windows 10. 我们另外使用了一台联想Lenovo s40-70 计算机模拟用户端, 配备有1.70 GHz Intel(R) Core(TM)i5-4210 四核处理器和4 GB 运行内存, 运行操作系统为Windows 10. 为测试方案性能, 我们借助Visual Studio 2017 的编译环境, 使用SQL Server 2017 数据库存储数据, 采用C# 语言编写Windows 窗体应用程序模拟实现去重过程, 限制网络传输带宽为10 Mbps. 利用OPENSLL 函数库[19]实现方案中所需的密码算法, 其中使用MD5 哈希函数生成数据标签, SHA-256 用于生成收敛加密密钥, 采用256 bit 强度的AES 实现数据加解密.

我们将不同体积的数据上传至云服务器, 并分以下三种情况进行模拟实验:

(1) 初始文件上传, 即上传CSP 中不存在的文件.

(2) 非流行文件的上传, 即上传文件为已存储在CSP 上, 但未超过流行度阈值的非流行文件.

(3) 流行文件的上传, 即上传文件为已存储在CSP 上的流行文件.

本节的主要内容包括方案的性能分析、计算开销、去重效率和方案特点对比四部分.

6.1 性能分析

我们从理论上对本文方案进行性能分析, 主要包括通信开销和存储开销, 并与Stanek 方案[11]进行对比. 对于数据M, CT、CC分别表示数据标签规模、密文规模, CK、Crk、Csk分别表示数据加密密钥规模、随机密钥规模和用户私钥规模. CID表示用户标识规模.

通信开销主要包括文件上传和文件下载两部分, 文件上传又分为初始文件上传、非流行文件上传和流行文件上传三种情况. 对比结果如表2 所示, 本文方案不会增加额外的通信开销. 对于文件的后续上传, 无论是非流行文件还是流行文件, 都不需要重复上传文件密文, 很大程度上节省了通信开销.

存储开销对比主要包括云服务器端、额外服务器端和用户端三部分. 我们设定数据M 为非流行数据,其合法用户数量为N. 对比结果如表3 所示, 本文方案无需额外服务器, 没有额外的存储开销. 实现了对非流行数据的去重, 相同数据在云服务器端只存储一份副本, 很大程度上节省了云服务端的存储空间.

表2 通信开销对比Table 2 Communication overhead comparison

表3 存储开销对比Table 3 Storage overhead comparison

6.2 计算时间开销

我们对本文方案的计算时间开销进行了测试, 测试的主要过程包含标签生成、所有权验证、密钥生成、数据加密和数据上传. 方案中公钥加密的数据体积较小, 计算时间忽略不计. 根据方案特点, 我们将不同体积的文件上传至云服务器, 分三种情况进行模拟实验. 情况1 为初始文件上传, 需要用户对数据进行双层加密并上传到云服务器, 该情况下的测试结果如图2 所示. 情况2 为非流行文件的上传, 此时需要用户根据收到的随机密钥自行计算外层加密密钥并存储, 不需重复上传文件密文, 该情况下的测试结果如图3 所示. 情况3 为流行文件上传, 此时用户只需对文件进行收敛加密, 并保存收敛加密密钥, 该情况下的测试结果如图4 所示.

对三种情况的总时间开销统计结果如图5 所示. 其中情况1 (初始文件上传) 下的总时间开销较大, 情况2 (非流行文件的上传) 和情况3 (流性文件的上传) 下不需要上传数据, 只需要少量的计算时间. 整体来看, 本文方案在时间开销方面具有明显的性能优势.

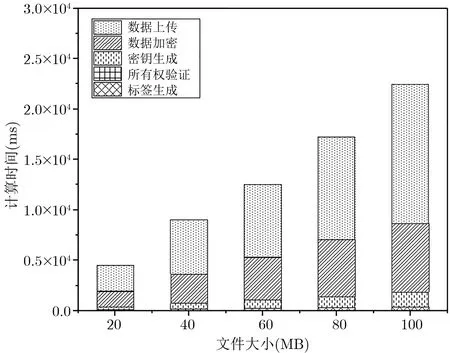
图2 初始文件上传Figure 2 Initial file uploading

图3 非流行文件上传Figure 3 Unpopular file uploading

6.3 去重效率

本文中去重效率的定义与其他主流方案[20]相同, 定义为用户需外包给CSP 存储的数据中重复数据体积所占总数据体积的比值.

为了模拟真实的应用场景, 在系统初始化阶段, 随机产生8000 个不同的文件, 文件大小随机, 上限为500 MB. 随机选取3000 个不同的文件存储到云服务器中, 为每个文件设定随机的合法用户数量. 设定流行度阈值为5, 并使得非流行数据占数据总量的比例不低于1/3. 测试方案的去重效率实验中, 随机选择指定数量的文件上传到CSP, 统计方案的去重效率. 将本文方案与PerfectDedup 方案[8]和Stanek 方案[11]进行对比, 数据去重效率实验结果如图6 所示. 三个方案都对数据进行流行度划分, Stanek 方案和PerfectDedup 方案只对流行数据去重, 但后者基于数据块去重, 去重效率高于前者. 本文方案实现了对非流行数据的去重, 同一数据副本在云服务器端只存储一份, 数据去重效率高于其他两个方案.

图4 流行文件上传Figure 4 Popular file uploading

图5 方案总时间开销Figure 5 Total time cost

图6 去重效率对比Figure 6 Data deduplication ratio comparison

6.4 方案特点对比

将本文提出的方案与ClouDedup[5]、PerfectDedup[8]、Stanek[11]在方案特点方面进行对比, 结果如表4 所示. 本文方案针对加密数据进行去重, 无需可信第三方, 对用户数据进行流行度划分, 实现了对非流行数据的去重, 可防止非授权用户下载.

表4 方案特点对比Table 4 Feature comparison

7 结论

本文提出了一种基于双层加密的云存储数据去重方案, 可实现云存储中加密数据的高效去重. 摆脱了第三方服务器的束缚, 去重方案更具有实用性. 通过划分数据流行度, 对隐私程度较高的非流行数据采用双层加密, 对隐私程度不高的流行数据采用收敛加密. 实现了非流行数据的去重, 进一步提高了去重效率.添加了额外的安全机制, 可有效的防止非授权用户下载数据, 保证云服务器上用户数据的安全性. 分析并讨论了方案的安全性, 实验结果表明本文方案具有较高的执行效率.