智能电网中可链接环签名的批量验证*

王启宇, 陈 杰,2, 庄立爽

1. 西安电子科技大学ISN 国家重点实验室, 西安710071

2. 西电密码研究中心, 西安710071

1 引言

随着人们对电力资源的需求日益增长, 传统电网在能源利用效率、环保性、安全性等方面已显现出许多隐患. 由于这些隐患的存在, 智能电网的概念应用而生. 智能电网是在传统电力系统基础上, 通过集成应用新能源、新材料、新设备和先进传感技术、信息通信技术和自动控制技术, 形成的具有高度信息化、自动化、互动化特征的新型现代化电网, 可以更好地实现电网安全、可靠、经济、高效运行. 根据美国国家标准技术研究所(NIST) 提出的智能电网概念模型[1], 智能电网由七个实体组成, 分别是发电站、输电网、配电网、用电客户、市场、服务提供方和操作中心, 其中前四个实体具有电力和信息双向流动的特征, 后三个实体主要负责智能电网的信息采集与电力管理. 智能电网利用先进的信息和通信技术对用户用电进行智能控制和经济管理带来方便的同时, 也存在用户隐私数据泄露的问题.

本文主要关注的是电力用户与操作中心间所传输信息的隐私保护, 即智能电网的安全性需求[2]. 同时智能电网要满足实用性需求, 也就是操作中心能够计算出所有用户的总耗电信息. 目前许多学者使用数据聚合的方法或匿名技术来实现以上的两个需求. 基于数据聚合所提出的方案可以保证不丢失基本信息、减少数据量、减少网络冗余和提高网络性能的前提下, 进行大量信息处理[3-10]. 2009 年Roberto 等人提出了一种基于同态加密的无线传感器网络数据聚合方案[3], 该方案使用对称密钥同态加密来保护信息的隐私性和完整性. 2012 年Lu 等人提出了隐私保护聚合方案[4], 该方案使用了超递增序列构建多维数据和同态加密技术Paillier 加密结构化数据. 2013 年Sushmita 等人在智能电网系统中提出了数据聚合与访问控制结合的安全策略[5], 该方案利用同态加密和基于属性加密技术. 2015 年Erkin 利用中国剩余定理以及同态加密等方法, 提出了一种面向智能电网的隐私保护数据聚合方案[6]. 2017 年Shen 等人根据Horner 规则和Paillier 同态加密体制提出了一个高效的具有隐私保护功能的立方体数据聚合方案[7]. 该方案能够对不同种类的数据进行区分和聚合, 但只能聚合同一时间点上的电力用户数据, 无法聚合单个电力用户在一段时间内的用电数据总和. 2018 年Asmaa 等人提出了一种基于轻量级格的同态隐私保护数据聚合方案[8], 该方案总通信量和计算负荷是微不足道的. 2018 年Lang 等人提出了一种多维数据的紧聚合方案[9], 该方案支持隐私保护和细粒度访问控制. 2019 年Prosanta 等人提出了一种轻量级, 隐私友好的基于掩模的空间数据聚合方案[10], 该方案用于安全预测智能电网中的电力需求. 接下来我们分析基于匿名技术所提出的方案[11-17]. 2011 年Cheung 等人采用了盲签名与匿名凭证的技术, 解决了电网安全中的隐私保护与认证问题[11]. 2014 年Yu 等人采用了环签名方法来实现电力用户的隐私保护[12], 引入环签名后可以降低系统要求, 避免生成大量的匿名凭证. 2014 年Badra 等人在保护电力用户隐私时, 提出了一种虚拟环结构[13]. 但由于虚拟环的特性, 该方案很难找出发布虚假消息的恶意用户. 2016 年Tan 等人在智能电网中使用假名提出了的隐私的数据收集方案[14], 该方案的假名注册过程中用到了环签名与零知识证明等技术. 2016 年Gong 等人在智能电网中提出了一种基于激励的需求响应隐私保护方案[15], 该方案使用离散对数创建假名, 并在假名注册的过程中用环签名来隐藏用户身份. 2018 年Guan 等人在智能电网中提出了一种高效的隐私保护聚合方案[16], 该方案使用布隆过滤器使得假名验证的验证速度有较大的提高.

由于假名的安全性基于假名证书的数量, 如果分配大量的假名会则会带来较大的存储开销, 并且造成假名的浪费. 而环签名主要的开销在于签名验证的计算量上, 所以我们提出同环批量验证的概念(如果签名选择的环成员保持不变, 那么我们便可以批量验证多个用户的多个环签名). 本文实现了环签名的批量验证[18]的同时, 引入了可链接消息标志技术[19]. 最后我们在智能电网系统中提出了批量验证的可链接环签名(BVLRS), 给出了详细的安全性证明和性能分析, 并指出不足.

本文的结构如下: 第2 节介绍了预备知识和系统模型; 第3 节提出了BVLRS 方案; 第4 节给出了该方案的安全性分析; 第5 节对该方案进行性能分析; 最后第6 节总结全文.

2 预备知识和系统模型

2.1 可链接消息标志方案(LIT)

可链接消息标志方案[19]由三个算法组成的L=(KGen,Tag,Link):

KGen(1λ): 输入安全参数, 通过概率算法输出标签密钥tk.

Tag(tk,m): 输入标签密钥tk 和消息m, 输出标签τ.

Link(m1,τ1,m2,τ2): 输入消息-标签对(m1,τ1),(m2,τ2), 通过确定性算法输出0 或1.

2.2 组合阶双线性对

文献[20]介绍了组合阶双线性对,利用群产生器G,输入安全参数λ,输出双线性对G.本文中G 输出N =p1p2p3,G,GT,e, 其中p1,p2,p3是不同的素数, 循环群G 和GT的阶为N =p1p2p3, e:G×G →GT是双线性映射, 组合阶双线性对满足下列性质:

双线性: ∀g,h ∈G, a,b ∈ZN, 满足e(ga,hb)=e(g,h)ab.

非退化性: ∃g ∈G, 若g 是群G 的生成元, 则e(g,g) 是群GT的生成元.

可计算性: g,h ∈G, 存在有效算法计算e(g,h).

2.3 复杂性假设

下面这些双线性群中的假设, 在文献[21] 中已定义.

假设 1 给定群产生器G, 我们定义了以下分布: G = (N = p1p2p3,G,GT,e)←RG, g←RGp1,X3←RGp3, D =(G,g,X3), T1←RGp1p2, T2←Gp1. 我们定义A 打破假设1 的优势是:

假设2 给定群产生器G, 我们定义了以下分布: G = (N = p1p2p3,G,GT,e)←RG, α,s ←RZN,g←RGp1, g2,X2,Y2←RGp2, g3←Gp3, D = (G,g,g2,g3,gαX2,gsY2), T1= e(g,g)αs, T2←RGT. 我们定义A 打破假设2 的优势是:

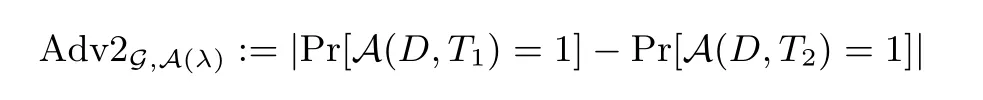
假设3 给定群产生器G, 我们定义了以下分布: G = (N = p1p2p3,G,GT,e)←RG, g,X1←RGp1,g2←RGp2, X3←RGp3, D = (G,g,g2,X1X3), T1←RGp1, T2←RGp1p3. 我们定义A 打破假设3 的优势是:

假设4 给定群产生器G, 我们定义了以下分布: G = (N = p1p2p3,G,GT,e)←RG, g,X1←RGp1,X2,Y2←RGp2, g3,Y3←RGp3, D =(G,g,g3,X1X2,Y2Y3), T1←RG, T2←RGp1p3. 我们定义A 打破假设4 的优势是:

2.4 系统模型

本方案的系统模型如图1 所示, 该系统一共包含三个部分: 操作中心(Control Center, CC)、区域网关(District Gateway, DGW) 和用户((User). 假设操作中心管理T 个区域, 每个区域网关分别对应DGW1,··· ,DGWT; 每个区域内有n 个用户, 记为L={ID1,··· ,IDn}, 下面给出各个实体的详细描述.

图1 系统模型Figure 1 System model

操作中心: 在该系统模型中, CC 是一个隶属于区域传输组织或独立系统运营商的实体. 在通信过程中CC 负责生成相关系统参数, 最后汇总通过区域网关DGW 所发来的用电信息.

区域网关(DGW): DGW 会收到本区域用户L={ID1,··· ,IDn} 发来的签名, 验证通过后, 汇总用户的总用电量与每个用户的总电量. 我们认为DGW 与CC 的通信是安全的.

用户(ID1,···,IDn): 每个用户都有一个智能电表, 负责收集该用户的用电信息. 对收集到的用电信息m 作签名, 发送给DGW.

2.5 安全模型

批量验证的可链接环签名方案由以下六个多项式时间内的算法组成:

初始化: 输入1λ, 其中λ 是安全参数; 输出主密钥α 和系统参数param. 用户的私钥空间范围是SK,消息空间范围是M, 身份空间范围是ID, 签名空间范围是SG.

密钥提取: 输入系统参数param, 用户身份ID ∈ID 和主密钥α; 输出用户私钥SKID∈SK.

签名: 输入param, L = {ID1,··· ,IDn} ∈ID, m ∈M 和私钥{SKIDπ∈SK|IDπ∈ID; 输出环签名σ ∈SG.

单个签名的验证: 输入param, L = {ID1,··· ,IDn} ∈ID, m ∈M 和签名σ ∈SG; 输出Valid 或Invalid.

批量验证: 输入param, L = {ID1,··· ,IDn} ∈ID, m ∈M 和η 个签名σ1,··· ,ση∈SG, 其中L1=···=Lη={ID1,··· ,IDn}; 输出Valid 或Invalid.

可链接验证: 输入param 和签名σ1,σ2∈SG; 输出Link 或Unlink.

3 批量验证的可链接环签名(BVLRS)

我们在智能电网系统中提出了批量验证的可链接环签名方案(BVLRS). 该方案引入了批量验证[22]和可链接的环签名, 并由以下六个步骤组成:

步骤1: 初始化

CC 选择一个阶为N =p1p2p3的双线性群G(其中p1,p2,p3是不同的素数). H0:{0,1}*→ZN和H1:{0,1}*×{0,1}*→ZN是两个哈希函数. 选定g,h,u,v,w ∈Gp1并将α ∈ZN作为主密钥. 公共参数是: param={N,g,h,u,v,w,e(g,g)α,H0,H1}.

步骤2: 密钥提取

每个用户ID 产生自己的私钥.随机生成r,y,tk--∈RZN,计算ID=H0(ID)和A=gαwy,B =gy,C =vy(uIDh)r,D =gr. 输出每个用户的私钥SKID={A,B,C,D,tk}.

步骤3: 签名

L = {ID1,··· ,IDn} 是区域网关中的n 个用户. 假定用户IDπ是真正的签名者, 其中IDπ∈L,π ∈{1,··· ,n}. 为了给用电信息m ∈{0,1}*签名, 用户IDπ计算IDi= H0(IDi), 其中i = 1 到n. 接着计算IDn+1=H1(m,L). 最后使用私钥SKIDπ={A,B,C,D,tk} 执行下列操作:

如果相等则验证成功, 否则验证失败.

步骤5: 批量验证

DGW 收到η 个签名σ1,··· ,ση，其中L1= ··· = Lη= {ID1,··· ,IDn}. 同步骤4 所述, 计算IDi=H0(IDi), 其中i=1 到n+1. 然后随机生成s,t1,··· ,tn+1--∈RZN, 同时检查:

如果相等则验证成功, 否则验证失败.

步骤6: 可链接验证

DGW 收到两个签名σ1={R1,Q1,m1,·}, σ2={R2,Q2,m2,·} 和公共参数param, 计算:

如果tag1=tag2, 则σ1和σ2具有可链接性, 否则不具有可链接性.

BVLRS 的交互流程是由CC 初始化整个系统, 生成主密钥和公共参数; 每个用户利用主密钥生成私钥, 之后对用电信息进行签名并发送给DGW; DGW 对收到的签名进行正确性和可链接验证, 流程图如图2 所示.

4 安全性分析

定理1 BVLRS 方案是正确的.

证明: 我们将私钥SKID代入到步骤4 中, 能够推导出:

图2 BVLRS 交互图Figure 2 BVLRS interaction diagram

因此等式(1)成立, 我们接着将私钥SKID代入到步骤5 中:

因此等式(2)成立, 那么BVLRS 方案是正确的.

定理2 BVLRS 方案在假设1-4 下, 具有不可伪造性.

在上述情况下要使式子(5)成立, 当且仅当要知道d mod p2的值. 敌手A 只知道w 和g ∈Gp1,

只与d mod p1相关, 所以敌手A 知道d mod p2的值发生的概率在理论上可以忽略不计.

在第二部分, 我们表明敌手无法伪造正常型的签名σpt1. 我们使用一些游戏来证明方案的安全性.

Gamereal: 该游戏是不可伪造的, 返回给敌手A 的密钥和签名都是正常的.

Gamert: 该游戏是被限制的游戏, 即敌手A 询问的身份与挑战者的身份不能是模p3相等的. 同时敌手A 生成的哈希值, 在模p3时也是可区分的(即敌手A 不能生成两个环身份集合和消息, (m, L) ／=(m′, L′), 但H1(m, L)=H1(m′, L′)).

Gamei: 该游戏前i 个询问的回答是半功能型的, 当大于i 时, 返回给敌手A 的回答是正常型的.

Gamek: 敌手A 在受限制的游戏Gamei和Gamei-1中时行为是相同的, 其中i=1 到k, k 是敌手A 第k 次询问. 我们知道敌手在游戏Gamei和Gamei-1, 赢得游戏Gamek的概率是可忽略不计的.

在下面的证明中, 假定敌手A 能够伪造正常型的签名σpt1.

我们知道在假设3 和4 下, 敌手A 在游戏Gamei中是受限制的, 其中i = 1 到k. 假定敌手A 产生两个身份ID 和ID′, 满足ID／=ID′但ID=ID′mod p3. 令P =gcd(ID-ID′,N). P 是N 的非平凡因子, 也就是P ∈(p3,p1p3,p2p3). 令q =N/P, 我们考虑下述两种情况.

接下来的证明中, 我们需要表明受限制的敌手A 在游戏Gamei-1和Gamei中的行为是相同的, 其中i=1 到k. 我们利用在文献[21] 中两个预言机O0和O1. 假定我们能够构造模拟器S 区分预言机O0和O1, 那么就能解决假设3 或者假设4.

此外, 敌手在游戏Gamek中构造模拟器S 去伪造正常型的密钥和签名σpt1, 即解决了假设2.

(1) 初始化: 模拟器S 构造(g,g2,g3,gαX2,gsY2,T), 为了判断T =e(g,g)αs是否成立. 参数设置如下所示: 随机选择α,a,b,c,d-- ∈RZN, 计算h = gb,u = ga,v = gc,w = gd∈RGp1, 选取两个哈希函数H0,H1, 得到公共参数param = {N,g,h,u,v,w,e(g,gαX2),H0,H1}. 将上述参数发给敌手A.

(2) 密钥询问: 回答关于身份ID 的密钥询问, 模拟器S 选择y,r,f --∈RZN并计算:

(3) 签名询问: 回答关于环 L = {ID1,··· ,IDn} 和消息 m 签名询问. 模拟器 S 随机选择f,λ1,r1,y1,··· ,λn,yn,rn,,yn+1,rn+1∈RZN, 其中λ1+···+λn+=0, 并计算:

模拟器S 判断T =e(g,g)αs是否成立, 若成立则解决了假设2.

最后我们证明σpt2={R,Q} 是不可伪造的.

假定敌手A 能够成功, 即(m*,R*,Q*) 是合法伪造. 根据定义, 我们知道(gQ*/R*)1/H0(m,*R*)=tag = gtk, gQ*= R*(gtk)H0(m*,R*), 所以(R*,Q*) 是关于m*的合法的Schnorr 签名. 我们知道如果DLP 问题[20]是困难的, 那么Schnorr 签名具有不可伪造性. 因此, σpt2={R,Q} 是不可伪造的.

定理3 BVLRS 方案是匿名的.

5 性能分析

5.1 通信开销

表1 通信开销分析Table 1 Analysis of communication cost

根据表1, 我们知道BVLRS 方案的通信开销略高, 由于我们增加了批量验证与可链接的功能, 会使签名的大小有所增加.

5.2 计算开销

首先, 我们分析BVLRS 方案的计算复杂度. 我们根据文献[24] 定义: E 代表幂运算, P 代表双线性对运算, Hf代表哈希函数运算, n 代表一个区域内电力用户的个数, η 代表签名个数. BVLRS 方案的计算复杂度分析, 如表2 所示.

表2 计算复杂度分析Table 2 Complexity analysis of BVLRS

表2 能够清楚的看出六个算法的计算复杂度. 接着, 我们将BVLRS 方案与其他标准模型下环签名方案进行对比, 对比如表3 所示.

表3 计算复杂度对比Table 3 Comparison of computational eきciency

根据表3, 我们知道四个方案中BVLRS 的单个签名验证的计算复杂度较高. 我们引用文献[24], 知道一次幂运算的时间是0.58 ms,一次双线性对运算的时间是10.31 ms,一次哈希函数运算的时间是3.58 ms.文献[18,25,26] 和BVLRS 的批量验证计算复杂度, 如图3 所示.

图3 验证时间对比Figure 3 Comparison of verification time

从图3 可知, 我们将环签名批量验证的复杂度从O(nη) 降到了O(n+η). 最后, 我们分析BVLRS 方案的安全特性并与其它方案作对比, 如表4 所示.

根据表4 可知, 我们的环签名具有可链接性. 这个特性能保证在区域网关DGW 在计算每个用户的耗电总量时, 而不知道用户的具体身份, 同时也可以根据此特性判断出恶意的电力用户.

表4 安全特性对比Table 4 Comparison of security features

6 结论

本文中BVLRS 方案在标准模型下是可证明安全的, 并可应用到智能电网的安全通信中. 通过安全性与性能分析, 我们知道BVLRS 方案具有匿名性, 不可伪造性, 可链接性. 可链接性能够保证在区域网关DGW 计算每个用户的耗电总量时, 不知道用户的具体身份, 但可以根据此特性判断出恶意的电力用户.我们将BVLRS 方案与其他标准模型下的环签名作对比, BVLRS 方案在选取的L 相等时, 通信开销会有所上升, 但该方案能够显著的降低环签名验证的计算开销.