支持国密算法的JavaScript 通用密码库的实现*

魏 荣, 郑昉昱, 林璟锵

1. 中国科学院 信息工程研究所 信息安全国家重点实验室, 北京100093

2. 中国科学院 数据与通信保护研究教育中心, 北京100093

3. 中国科学院大学 网络空间安全学院, 北京100049

4. 中国科学技术大学 网络空间安全学院, 合肥230026

1 引言

Web 应用是指以B/S (浏览器/服务器, Browser/Server) 模式提供服务的网络程序, 相对C/S (客户端/服务器, Client/Server) 架构的传统桌面应用而言, 其具有跨平台、兼容性好、维护成本低、免安装的优势, 因而在近年来迅猛发展, 甚至曾一度出现了Web 应用取代桌面应用的呼声.

当然, 在未来相当长的一段时期内, Web 应用都难以完全淘汰桌面应用, 因为它受到了本地资源访问限制、网络设施建设等因素的影响, 除了在功能丰富度方面无法与桌面程序比拟外, 其响应速度也极度依赖网络性能, 常出现内容加载缓慢等问题, 而最致命的还是Web 技术在实现密码运算时天然存在的短板:

(1) Web 应用的鉴权过程往往需要将用户口令发送到服务端进行比对, 尽管客户端会使用加盐哈希来予以一定保护, 但仍不能彻底解决窃听、重放等问题;

(2) 虽然一些口令身份鉴别机制可以让Web 应用不用发送口令信息就能完成密钥协商, 例如EKE(Encrypted Key Exchange)[1]、J-PAKE (Password-Authenticated Key Exchange by Juggling)[2]等, 但需要客户端能够完成较为复杂的密码运算——如果以浏览器密码插件的形式实现, 则要求插件程序兼容各个系统平台和浏览器内核, 维护成本较高; 而如果让JavaScript 来完成这部分工作, 则要求浏览器内核对JavaScript 的解释速度足够快, 以免影响用户体验;

(3) 虽然浏览器都内置了HTTPS (Hyper Text Transfer Protocol over Secure Socket Layer, 超文本传输安全协议) 功能, 但该功能只提供统一的认证、加密和完整性保护服务, 开发者无法利用其内置的密码算法来实现自定义的安全协议.

不难看出, 让JavaScript 承担密码运算工作是Web 应用发展的大势所趋, 由于终端设备和浏览器多种多样, 性能良莠不齐, 难免有人担心作为脚本语言的JavaScript 无法胜任复杂运算工作(如椭圆曲线标量乘). 不过, 随着近年来计算机硬件性能大幅度提升和浏览器内核更新换代, JavaScript 的执行速度已经有了很大改观, 可以胜任复杂密码运算的工作, 尤其是移动互联网时代的到来和HTML5[3](HyperText Markup Language 5, 超文本标记语言5) 技术的发展, 使得Web 应用在智能移动终端中也大放异彩. 让前端脚本承担更多力所能及的计算工作已然时机成熟.

而在我国, 由于计算机硬件、操作系统和软件设施建设长期落后国际水平, 导致缺乏基本的国产化软硬件平台, 国产密码推进工作迟滞. 虽然SM2[4-8]、SM3[9]和SM9[10-14]算法已经上升为国际标准, 但要得到主流浏览器内核的支持, 还有相当长的路要走. 目前也只有360[15]、密信[16]、赢达信[17]等个别企业推出了支持国密算法的浏览器产品, 其普及度还很低, 而国内为数众多的Web 应用都还在使用国外密码算法来保障数据安全, 其中不乏MD5、SHA-1、DES、RSA-1024 等已经被建议淘汰或明令禁止的不安全算法.

值得高兴的是, 使用JavaScript 实现密码算法不必拘泥于软硬件平台的限制, 这意味着我们可以方便地使用国产密码算法, 不用考虑浏览器是否支持的问题.

2 研究问题与现状

我们旨在用JavaScript 实现一款适用于Web 应用的通用密码库, 可以提供国密SM2、SM3 和SM4[18]算法, 并保证该库压缩后的大小控制在50 KB 以内.

在Web 应用中, JavaScript 的性能体现在加载速度和执行速度两方面, 而这两者往往处于对立关系. 例如, AES (Advanced Encryption Standard, 高级加密标准) 算法在OpenSSL 中的实现采用了TTable[19]和循环展开的技巧, 前者将状态矩阵每一列的列混淆和字节代替操作融合在一张1 KB 大小的查找表中, 只需一次访存就可以完成上述变换, 还可以省略行移位步骤, 但该方法需要加密和解密函数各自维护4 KB 大小的查找表, 这在本地应用中并不算很大的存储负载, 不过在Web 应用中, 从服务端下载8 KB 的查找表会明显增加网络延迟; 循环展开方式也存在类似问题, 以AES-128 为例, 如果将循环展开,则会导致主函数代码量增加近十倍, 同样会显著增加网络延迟. 因此, 在实现算法时, 应权衡代码量和执行速度之间的利害取舍, 对可以通过少许代码预计算出来的常量, 尽量延后到本地生成, 以减小流量消耗, 但也要注意, 预计算的时间开销不宜过长.

当然, 针对JavaScript 难以进行高性能计算的问题, 最理想的解决方案还是尽可能利用设备本地的资源和计算能力, 这样不仅可以避免重复下载密码库, 还可以省去脚本解释执行的漫长过程, 在Web 技术的发展过程中, 也确实产生了很多相关的支撑技术, 例如现代浏览器普遍支持的JIT (Just In Time,即时) 编译技术[20]大大弥补了JavaScript 作为脚本语言的天然速度劣势; 此外, 还出现了WebGL[21]、WebAssembly[22]、和asm.js[23]等更深程度的优化执行技术, 它们力求让JavaScript 的运行速度能够媲美Native 代码, 然而, 除了浏览器支持程度不理想外, 其较大的编译输出会严重增加下载时间; 随着HTML5 技术的发展, 一些主流浏览器也加入了对Web Worker[24]的支持, 从而改变了长期以来JavaScript 只能单线程执行的状况, 让Web 应用也开始步入并行计算的时代.

上述各种技术的演进都是以提升用户体验为导向的, 其优先考虑的是页面渲染和响应速度, 而非数据安全问题, 密码库的开发者可以对其加以利用, 以提高密码计算效率, 但敏感数据的安全暂时还要靠浏览器的隔离机制来保证.

考虑到浏览器中的数据安全问题, W3C (World Wide Web Consortium, 万维网联盟) 于2017 年正式提出了关于Web Cryptography API[25]的建议, 期望能够以JavaScript 接口形式为Web 应用提供基础的密码服务, 各主流浏览器也开始加入对上述接口的实现. 由于处于更底层位置, 这类密码服务的性能远比第三方JavaScript 密码库更接近Native 代码[26], 但截至目前, 不同浏览器所实现的算法集合或多或少都存在差别, 只有极个别浏览器(如Samsung Internet[27]) 完整实现了所有API[28]. 因此, 在未来很长一段时期内, Web 开发者依然需要集成自己的JavaScript 密码库以备不时之需.

可见, 即便是应用广泛的国际算法, 也未能如HTTPS 一般成为浏览器的标配功能, 而在国外厂商占据主流浏览器市场的今天, 国产密码算法要得到浏览器的集成则更是任重道远. 2017 年, 中科院DCS 中心研制了通过Windows CNG[29]接口提供服务的国产商用密码算法库, 并基于该库研制了支持商密算法的Edge 浏览器和IE 浏览器[30], 上述两款浏览器利用了操作系统的密码服务来为Web 程序提供更安全的密码功能, 这也是未来Web 密码服务形态的一大发展方向——Web 应用中的密码服务最终是要沉降到更为快速和安全的浏览器内核甚至操作系统中来实现的. 但与前文所述的技术类似, 上述产品也仅仅提供了基于Windows 10 系统上两种浏览器的密码服务, 并不具备普适性, 鉴于我国在操作系统和浏览器领域长期落后的现状, JavaScript 库仍将是国产密码算法入驻浏览器的主要形态.

3 实现方案

本节主要阐述JavaScript 库中对国密算法的实现和优化方案, 并不介绍原算法过程, 读者如果想了解算法原理, 可以查阅相关国密标准[4-8,18,31].

3.1 实现思路

目前已经有很多较为著名的JavaScript 国际密码算法库, 如clipperz[32]、OpenPGP.js[33]、sjcl[34]、jwcrypto[35]、cryptico[36]、jscrypto[37]和cryptojs[38]等. 综合考虑文件大小、代码架构、密码算法集合和优化程度, 我们决定基于sjcl 库完成对国产密码算法的集成和优化.

sjcl 是由斯坦福大学Stark 等于2009 年推出的一款适用于浏览器和Node JS 平台的JavaScript 密码库, 该库最初围绕AES 算法进行优化实现, 随着版本演进, 目前已经能够支持国际上常用的对称、非对称密码算法、哈希算法、消息认证函数、KDF (Key Derivation Function, 密钥派生函数) 以及随机数发生函数, 成为了一款比较全面的密码套件, 该库还针对脚本加载速度进行了一定程度的优化, 以提升用户体验.

相比上文中其他较流行的密码库, sjcl 重点关注密码原语的优化实现, 而非更高层的通信或密码协议,因此非常精简, 具有更小的体量和更好的兼容性, 这不仅体现在平台兼容性上(它通过了Mac、Linux 和Windows 系统下所有主流浏览器的测试), 还体现在对旧的ES5[39](ECMAScript 5) 标准的完美兼容上.

更重要的是, sjcl 库的模块化代码结构对二次开发非常友好, 各个模块之间的松散耦合便于开发者根据实际需要选择性地打包, 随时去除不必要的功能, 这有利于缩减文件大小, 同时也让该库具备了很好的可扩展性, 新算法的集成工作比其他同类库更为方便. 此外, sjcl 库一直致力于针对Web 应用场景对密码算法进行特殊优化[34], 相比同类密码库, 它在文件大小和运算速度之间达到了较好的平衡[26].

我们基于sjcl 密码库的框架, 用JavaScript 实现了SM2 签名和加密算法、SM3 摘要算法和SM4 对称加密算法, 支持浏览器和Node JS 平台, 接口与sjcl 库保持了风格一致, 继承了其调用简单的优点; 与此同时, 针对最为耗时的ECC (Elliptic Curves Cryptography, 椭圆曲线密码学) 算法, 我们也进行了一定程度的优化, 将ECC 密钥生成和签名速度提升了一倍.

3.2 对SM2 算法的优化

由于sjcl 库代码架构的原因, 对SM2 算法的优化实际上也可以惠及库中其他ECC 算法.

对ECC 椭圆曲线算法的优化通常集中在最为耗时的点乘运算上, sjcl 库用了常见的固定基窗口方式[40]来加速点乘, 但没有对乘法标量进行长度扩充, 使其与椭圆曲线基点的阶等长, 容易在时序分析下暴露乘法标量(如私钥) 长度信息, 当然, 这只是一个小问题, 我们对其进行了修复.

考虑到内存占用和预计算的时间开销, sjcl 库所选的窗口宽度为4. 例如, 对256 位长的标量乘数t 和点P, 通过64 次“访存-16 倍点-点加” 操作来完成[t]P 运算, 步骤如下:

(1) 将t 表示为16 进制:

(2) 计算所有Pk=[k]P, 其中k =0,1,··· ,15;

(3) 按公式(1)计算[t]P:

还有一种固定基的comb 方法[9], 以另外一种形式来分割乘法标量, 通过64 次“访存-2 倍点-点加”操作来计算[t]P, 但是乘法标量的预处理和查找表的预计算也相对更繁琐一些. 以模长l = 256, 窗口宽w =4 为例, 使用固定基comb 方法计算[t]P 的步骤如下:

(1) 将t 表示为二进制, 并均分为4 部分:

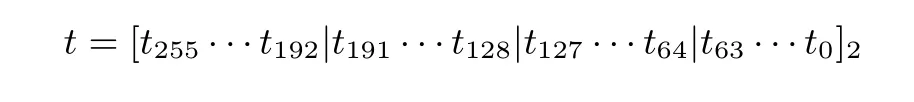
(2) 计算所有[2192s3+2128s2+264s1+s0]P, 记作Pk, k =s3|s2|s1|s0, s0、s1、s2和s3为0 或1;

(3) 按公式(2)计算[t]P:

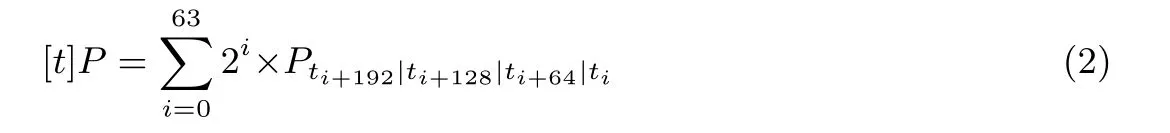
与窗口方法不同, comb 方法的预计算无法只通过点加和倍点完成, 需要调用点乘方法, 因而不能在点乘运行时进行. 该方法更适合将预计算结果直接硬编码在程序中, 但这种做法与sjcl 库精简代码、降低下载流量的设计原则不符, 加之预计算比窗口方法耗时, 最终没有被sjcl 库采纳.

不过, 对于固定点(如椭圆曲线基点) 乘法来说, comb 方法只需在曲线初始化时进行一次预计算即可,我们为曲线基点编写了单独的点乘方法, 使用comb 方法省去了75% 的倍点运算, 让基点的点乘运算速度提升了约110%, 从而加速了ECC 密钥生成和签名过程. 在Maxthon 浏览器中, ECDSA (Elliptic Curve Digital Signature Algorithm, 椭圆曲线数字签名算法) 和SM2 签名算法优化前后的性能数据如表1 所示:

表1 ECC 优化前后性能对比Table 1 Performance with and without optimization for ECC

另外, SM2 签名算法中, 对消息的预处理需要公钥参与, 而每次重复计算公钥会造成显著的时间开销,我们在生成和导入密钥对时, 将公钥也保存在了私钥对象中, 以节省一次不必要的标量乘.

在支持多线程的平台上实现上述两种优化方法时, 如果将公式(1)和公式(2)分派给多个线程去运算,还可以获得成倍的加速效果. 例如: 在固定基comb 方法中, 如果将i ∈[0,31] 和i ∈[32,63] 部分的累加工作分派给两个子线程去完成, 最后在主线程中合并结果, 从理论上来讲, 就可以获得近两倍的加速效果.

就固定基comb 方法应该使用多少线程的问题, 我们曾用C 语言在64 位PC 平台(4 核处理器) 和ARM 平台(8 核处理器) 上分别测试了开启1、2、4、8 个子线程时的SM2 点乘运算速度. 实验表明, 在开启4 个子线程时, 速度达到了最佳——可见, 并不是线程数越多, 并行度越高, 效率就越高, 如果线程太多, 而每个线程的计算量太小, 则线程创建和销毁的开销在运行时间中的占比也会升高, 变得不可忽略, 反而导致性能下降.

不幸的是, 由于浏览器中UI (User Interface, 用户界面) 渲染线程和JavaScript 引擎对DOM (Document Object Model, 文档对象模型) 树的访问是互斥的, 曾经有很长一段时间, 为了保证线程安全,JavaScript 都不提供多线程机制. 虽然HTML5 提供了Web Worker 机制, 允许将不访问DOM 的JavaScript 代码放在后台线程中运行, 但它要求将子线程需要用到的所有对象和函数结构化拷贝到新的上下文环境中, 而一次这样的拷贝往往要耗时上百毫秒, 其线程本身的开销远远高于C 语言, 可见Web Worker 机制的主要用途在于确保执行脚本时不阻塞页面渲染, 而非高性能并行计算. 因此, 我们最终决定基于单线程JavaScript 来完成实现.

3.3 关于SM3 和SM4 的实现

JavaScript 作为一种弱类型的脚本语言, 默认的number 类型为64 位双精度浮点数, 相当于C 语言中的double 类型. 但是在参与位运算时, 会默认转化为32 位整数, 也就是说它并不支持32 位以上的长整数, 这不利于实现高性能的密码学大数运算, 好在SM3 和SM4 算法中的位操作所针对的至多是32 位长的字, 不会受到影响.

sjcl 库的AES 算法实现采用了T-Table 优化, 而前文也提到过, 这种方法需要维护8 KB 大小的查找表, 不宜直接使用硬编码方式, Stark 等人将S 盒、逆向S 盒以及扩展查找表都放在预计算阶段中, 在第一次调用AES 算法时才会动态生成上述查找表, 而只存储了硬编码的轮常量. 需要注意的是, Web 应用场景下, 敌手更容易获得加密耗时, 进而发起时序攻击, sjcl 库在使用T-Table 方案时, 在AES 函数首轮和末轮放弃使用T-Table 表, 转而选择了查找S 盒的传统方式, 这可以在一定程度上防止基于缓存的时序攻击.

与SPN (Substitution-Permutation Network, 代替-置换网络) 结构的AES 算法相比, SM4 算法则属于非对称Feistel 结构, 其轮函数的处理对象也迥异于AES 算法的4×4 状态矩阵, 从理论上来看, 对SM4 使用T-Table 方案所能产生的优化效果虽然远不如AES, 但在编码时, 也理应能在每轮处理中节省7 次位操作.

SM4 算法分组长度 16 字节, 需要进行 32 轮变换, 将第 i 轮状态记作 4 个 32 位字:(Xi,Xi+1,Xi+2,Xi+3), 记第i 轮轮密钥为Ki, 其中i=1,2,··· ,32, 则轮变换步骤如下:

(1) A=(a0,a1,a2,a3)=Xi+1⊕Xi+2⊕Xi+3⊕Ki;

(2) B =(b0,b1,b2,b3)=(S[a0],S[a1],S[a2],S[a3]);

(3) C =B ⊕(B ＜＜＜2)⊕(B ＜＜＜10)⊕(B ＜＜＜18)⊕(B ＜＜＜24);

(4) Xi+4=Xi⊕C.

步骤(2) 中, 符号S 表示查找S 盒. 而在T-Table 方案中, 可以将步骤(2) 和步骤(3) 合并如下:

(1) y =S[x],x=0,1,··· ,255;

(2) Ti[x]=(y ⊕(y ＜＜2),y ⊕(y ＞＞6),y ＜＜＜2,y ＜＜＜2)＞＞＞8i,i=0,1,2,3.

上述步骤(2) 就是借助SM4 的S 盒生成T-Table 查找表的方法. 我们测试了SM4 算法T-Table 方案的优化效果, 结果很出乎意料——在JavaScript 实现中, 采用T-Table 的SM4 加密速度略慢于未优化版本. 经过实验与分析, 我们发现查找T-Table 表的耗时超过了查找S 盒一倍, 可见至少在测试浏览器的JavaScript 解释器下, 对32 位字的访存所消耗的机器周期要多于对字节的访存, 这一点与Native 代码有着明显差异.

除了T-Table 外, bit slicing[41]也是一种常用于对称加密算法的优化技巧, 可以实现对大规模数据的并行处理. 然而, AES 和SM4 的S 盒是基于有限域理论设计的, 在bit slicing 实现时会分解为大量位操作[42,43], 这意味着JavaScript 代码量的急剧增加, 因此并不适合在Web 应用中采用.

基于以上考虑, 我们最终采用了原始版SM4, 虽然加密轮数多于AES, 速度也比T-Table 版AES 要慢很多, 但只需维护256 B 大小的S 盒即可. 由于预计算S 盒的代码量超过了硬编码的大小, 直接使用硬编码方式更为合理.

4 性能测试

由于缺乏可横向对比的同类通用密码套件, 我们仅对扩充后的sjcl 库进行了测试, 并对国密算法和参数规模与之相当的对应国际算法进行了性能对比.

4.1 测试环境

我们通过脚本将源代码打包成了47 KB 的密码库文件, 并在64 位Windows 平台上, 使用了三种主流浏览器和一款国产浏览器进行性能测试, 测试平台的具体型号、配置和版本如表2 和表3 所示.作为最具代表性的浏览器, 上述几种平台均在不同程度上实现了Web Crypto API, 但目前都不支持国产密码算法.

表2 系统/硬件平台Table 2 System/Hardwares

表3 软件平台Table 3 Softwares

4.2 测试结果

我们分别对比了ECDSA 和SM2 签名算法、SHA-256 和SM3 哈希算法以及AES-128 和SM4 对称加密算法的性能, 结果分别见表4、表5 和表6.

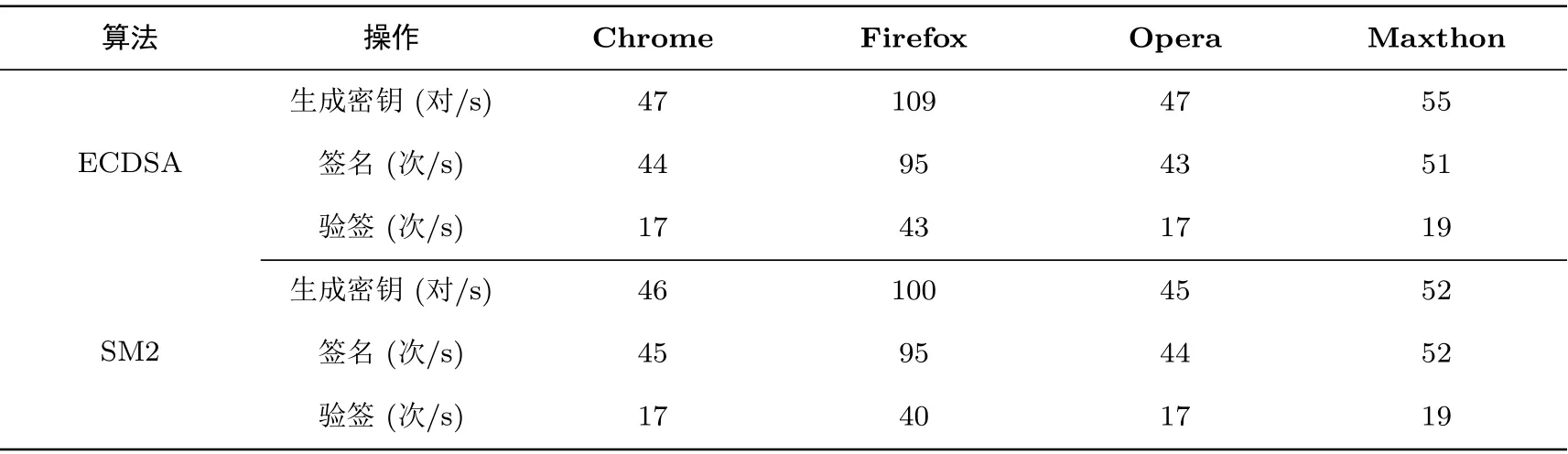
表4 ECC 签名算法(单线程) 性能Table 4 Performance of ECC Signature Algorithms (with Single Thread)

表5 哈希算法性能(Mbps)Table 5 Performance of Hash Algorithms (Mbps)

表6 对称加密算法性能(Mbps)Table 6 Performance of Symmetric Encryption Algorithms (Mbps)

由于我们对定点标量乘进行了优化, 因此ECC 算法中涉及基点乘法运算的密钥生成和签名过程要比验签快很多.

T-Table 方法旨在节省对称加密算法查找S 盒之后的混淆和扩散步骤, 与S 盒类似, Feistel 结构的算法(如DES、SM4) 加解密过程共用一套T-Table 查找表, 而AES 则不然, 并且在使用该方法对AES 算法进行优化时, 由于解密过程中的逆向字节代替无法融入查找表, 所以优化程度较加密过程要低, 从表6 中可以看出, AES 算法的加密速度要高于解密速度.

Maxthon 浏览器实际上使用了Chrome 的webkit[44]内核并作出了优化, 其内置JavaScript 引擎为Chrome V8[45], 因此二者性能都很接近使用Carakan[46]引擎的Opera 浏览器. 相对于Chrome 而言,FireFox 所使用的SpiderMonkey[47]引擎显然具有更高的计算性能.

5 结论与展望

我们基于sjcl 密码库, 实现了JavaScript 版国密SM2、SM3 和SM4 算法, 形成了一款新的通用密码套件, 可以为Web 应用提供适度安全的前端通用密码服务. 此外, 我们使用固定基comb 方法对椭圆曲线点乘进行了加速, 将ECC 密钥生成和签名的运算速度提升了一倍以上.目前存在的问题和下一步工作:

(1) 虽然实现了SM2 等非对称算法, 但使用场景十分有限, 不论是安全性还是功能都无法与驱动加硬件Key 的模式相比, 目前至多可以用于J-PAKE 等协议以及加密、验签工作, 在未来工作中,我们将考虑利用拆分或口令派生机制, 予以私钥更高等级的保护;

(2) 目前所实现的SM4 算法系基础版本, 在部分平台上比sjcl 的AES-128 慢一倍左右, 我们也尝试过利用SIMD.js[48]或bit slicing 来进行优化, 但没有得出可行有效的方法, 反倒是AES-128 可以利用SIMD.js 进行向量化实现, SM4 可能还存在软件优化空间, 希望下一步工作中能够找到有效方法来提升其性能;

(3) 在移动互联网应用中, HTML5+Native 的架构大行其道, 它用Web 代码来实现需要跨平台的核心功能, 极大地简化了开发工作, 还让HTML5 可以方便地访问移动终端Native 资源, 如传感器、相机、通信录等, 这在传统PC 上是很难实现的, 因此可以很大程度上解决Web 应用功能受限的问题, 而这也给了我们新的启发——至少在移动端上, 能否利用对Native 的访问来扩展非对称密码算法的应用场景, 实现移动软件Key 的效果？能否利用Native 资源为移动Web 应用构造高质量的随机数发生器？我们相信这些设想都值得在下一步工作中去尝试.