空气中快堆堆芯单组件的非线性动力学响应分析

2020-11-05王卓勋代成栋黎昭文翊仁

四川轻化工大学学报(自然科学版) 2020年5期

王卓勋，代成栋，黎昭文，李鹏，杨翊仁

(1.西南交通大学力学与工程学院，成都 610031；2.中国核动力研究设计院，成都 610041)

引言

随着现代社会的发展，能源的需求越来越大。由于化石能源不可再生且排污量大，逐渐被新型能源所替代。核能作为新能源，由于其发电效率高、污染量小、安全等优点越来越受到各国重视。近年来，我国在大力发展核电，主要以压水堆为主[1]，快堆作为新型的核反应堆[2]，相比于压水堆具有更高的热效率和铀资源利用率，发电效率更高，有着重要的研究意义和广阔的应用前景。

燃料组件作为快堆堆芯重要组成部分，在地震来临时，燃料组件与其他组件之间会发生相互碰撞，进而组件发生变形，组件的空间分布结构也会发生变化，因而对其进行抗震分析具有非常重要的意义。对于快堆组件的抗震分析，使用的有限元程序有法国CEA的CASTEM-2000，日本HITACHI的SAFA[3]，通用商业程序如ANSYS、MARC及ABAQUS等。中国原子能科学研究院引进了日本商业有限元软件FINAS，并且使用该软件对快堆堆芯组件进行了单组件、单排组件及多排组件的抗震分析计算[4-5]，将一些结果与ANSYS计算结果进行对比，获得了较好的结果。

快堆堆芯组件结构与压水堆堆芯组件结构有所不同[6]，对于某些关键问题的处理也有所不同。对于快堆堆芯模型，李海龙[7]和莫亚飞[8]对其进行了研究，以梁来建立组件模型，对组件带有接触碰撞效应的位置一般采用弹簧间隙元模拟，固定及承重的位置一般采用简支条件进行模拟，并对单根以及单排组件进行了动态响应分析。由于快堆堆芯内存在液钠，需要考虑液钠对组件的影响。王万惠[9]对流体附加质量方法进行了研究，用微分法推导出了附加质量计算公式，计算了在水中单根以及两根组件的碰撞力。商超皓[10]对流体变化附加阻尼进行了研究，采用ANSYS生死单元技术，模拟了组件之间随间隙变化而变化的流体附加阻尼，计算出了组件的最大位移以及最大碰撞力。快堆组件的弯曲刚度是十分重要的参数，Ma[11]等人对组件的弯曲刚度进行了相关的实验研究。Thomas[12]等人考虑组件的非线性阻尼，对组件进行了非线性动力学的实验和数值仿真分析。然而，目前国内针对燃料组件特别是快堆燃料组件结构动力学的计算主要是以已有商业软件为主，缺少针对该问题的理论研究及相关计算程序的开发设计。

本文基于有限元方法[13]，以中国实验快堆为例[4]，对快堆堆芯组件的建模方法和建模参数进行了研究，并编制了计算程序。首先，对单根快堆堆芯燃料组件进行建模和自由振动分析，同时采用通用有限元软件ANSYS对单根堆芯组件进行建模和自由振动分析[14-16]，将计算结果与ANSYS以及文献[4]的计算结果进行对比；然后，给定组件凸台处初始位移激励，对组件与刚性壁面碰撞的振动响应及碰撞特性进行了计算和分析；最后，给定组件球座支撑处简谐激励，对组件在简谐激励作用下的振动响应及碰撞特性进行了计算和分析。本文的分析研究对燃料组件特别是快堆燃料组件的抗震计算研究具有一定的参考意义。

1 燃料组件的建模与自由振动分析

已有的理论及实验研究表明，燃料组件的振动主要表现为梁的横向弯曲振动。针对组件横向振动问题，基于有限元方法编制了计算分析软件(以下称本文软件)。图1(a)给出了建模示意图，图中黑点为组件建模关键点，关键点由下往上编号排序，整个梁模型含有25个关键点。根据文献[4]的等效方法将燃料组件简化为7段具有不同横截面面积和弯曲惯量参数的梁，每段梁的参数见表1。本文软件将要完成组件自由振动、组件与刚性壁面碰撞及组件在简谐激励作用下的3种典型工况的计算和分析，3种计算工况所建立的模型分别如图1(b)～图1(d)所示。

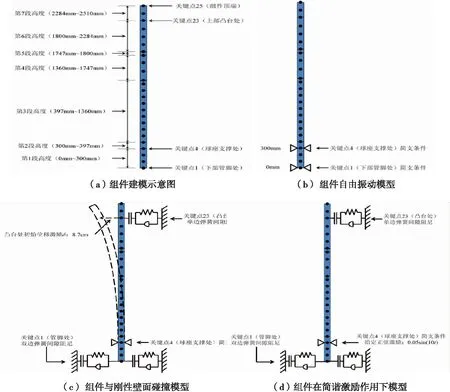
图1计算模型及计算工况示意图

表1燃料组件参数

在组件的自由振动分析计算中考虑组件的剪切效应，将组件的下部管脚与管座之间及组件的球座支撑处均模拟为简支约束，组件其余部分自由，模型见图1(b)。计算提取前3阶固有频率和模态，并将频率结果与ANSYS以及文献[4]的结果(采用FINAS软件进行计算)进行对比(表2)，计算模态结果与ANSYS的对比如图2所示。从表2与图2所示的结果来看，本文软件的计算结果与文献[4]结果吻合较好；但第三阶频率而言，ANSYS和文献[4]的计算结果都与本文差距较为明显，因为本文软件采用的是考虑剪切系数修正梁形函数的建模方式，这与其他两种软件对组件剪切效应的处理方式不同。

表2本文软件计算固有频率与ANSYS的对比

图2 模态结果的对比

2 燃料组件与刚性墙壁的碰撞的建模与分析

对燃料组件与刚性壁面的碰撞过程进行分析，此工况下的燃料组件的弯曲惯量见表1。地震工况时，燃料组件的上部凸台间及组件的下部管脚与管座之间都会有接触碰撞作用，球座支撑可视为组件的一个固定点，支撑整个组件的重量。因此，图1(c)中，建模采用单边的间隙弹簧阻尼单元来模拟组件上部凸台与刚性墙壁碰撞的作用，间隙值为0.15 mm，阻尼值为124.5 N/(m/s)，弹簧刚度设为2×107N/m；球座支撑处采用简支约束进行模拟；下部管脚与管座之间的碰撞作用的模拟则采用双边弹簧间隙阻尼单元，间隙值都设为1.5 mm，阻尼值都设为102.5 N/(m/s)，弹簧刚度都设为2×107N/m；对于组件的结构阻尼系数，α为1.376 43 s-1，β为4.792 024×10-4s。

图1(c)中，在组件上部凸台(即模型中的23关键点)处给定初始位移激励δ=8.7 cm，计算组件在自由释放后的振动响应及碰撞力。图3给出了凸台处的位移(dx)-时间(t)曲线，由图3可知，由于凸台处受到了单向约束，因此组件的振动主要发生在负向；由于阻尼的作用，组件的振动响应趋势呈周期性衰减规律；图3中下部灰色区域为碰撞区域。图4给出了凸台处的碰撞力(F)的计算结果，由图4可见，最大碰撞力出现在第一次碰撞时(时间为0.075 s)，此时最大碰撞力约为11 kN，随后碰撞力呈现显著的衰减趋势，这也与凸台位移随时间的衰减规律一致。

图3组件上部凸台位移-时间曲线

图4组件上部凸台右端碰撞力响应

凸台处最大碰撞力与凸台处弹簧刚度之间的关系如图5所示。调整凸台处的弹簧刚度以分析凸台处的最大碰撞力的影响规律。由图5可见，随着凸台处弹簧刚度(K)的增加，凸台处的最大碰撞力(Fmax)也呈现出增加的趋势。调整管脚处左、右两端的弹簧刚度，计算得到不同刚度(K)对应的管脚左、右两端最大碰撞力(Fmax)分别如图6、图7所示，从图6与图7可知，管脚左、右两端的最大碰撞力随管脚左、右两端的弹簧刚度的增加而呈现非线性的增加趋势，当刚度较小时，最大碰撞力的变化较为剧烈，当刚度较大时，最大碰撞力的变化较为平缓。凸台处的最大碰撞力(Fmax)随着管脚弹簧刚度(K)变化具有典型的非线性变化关系，如图8所示，在刚度没到达2×107N/m时，最大碰撞力随刚度的增加而增加；刚度到达2×107N/m时，最大碰撞力达到一个峰值；刚度超过2×107N/m时最大碰撞力逐渐减小，逐渐收敛于一个值。这也表明，适当的增加管脚弹簧刚度有利于改善凸台处的碰撞特性。

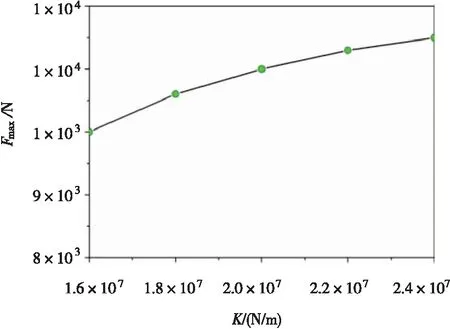
图5凸台处最大碰撞力与凸台处弹簧刚度曲线

图6 管脚左端最大碰撞力与管脚弹簧刚度的变化

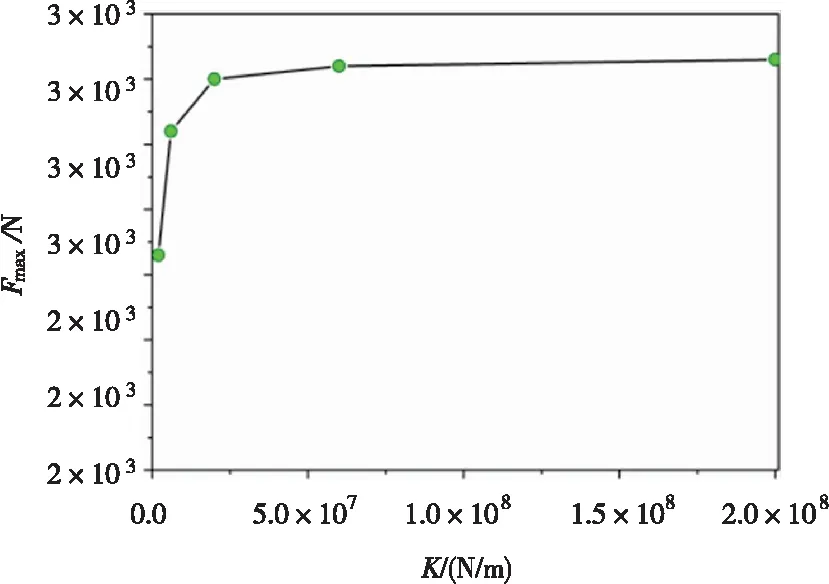
图7 管脚右端最大碰撞力随管脚弹簧刚度的变化

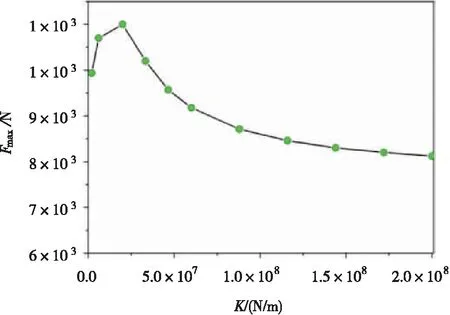
图8 凸台处最大碰撞力随管脚弹簧刚度的变化

3 简谐外激励作用下燃料组件的动态响应

图1(d)中，在组件关键点4处即球座支撑处施加水平方向的正弦激励(激励曲线：0.05sin(10t)，加载时间：4 s)，以考察组件模型对简谐激励的响应。燃料组件管脚处的位移(dx)-时间(t)曲线如图9所示。由图9可见，组件响应趋势也呈周期性变化，组件位移达到管脚处设置的间隙值(图中红线处)时，组件会受到弹簧的阻挡，从而位移增速减缓。由于燃料组件上部凸台处左端没有约束，因此该系统具有明显的非对称性，从而限制了凸台处正向的移动，导致管脚处负向位移最大值小于正向位移最大值。管脚处的左、右两端碰撞力(F)响应分别如图10、图11所示，由图10和图11可知，组件的碰撞力也呈周期性的变化；左端最大碰撞力发生在2.51 s时，约为6.37 kN；右端最大碰撞力发生在2.67 s时，约为14.2 kN，这主要也归结于此模型的非对称性。凸台处的位移(dx)-时间(t)曲线如图12所示。由图12可知，凸台处的位移呈周期性变化，图中下部灰色区域为碰撞区域。凸台处的碰撞力(F)响应如图13所示。由图13可见，凸台处碰撞力大致呈周期性变化，其中最大碰撞力发生在 3.13 s时，约为49.7 kN。

图9管脚处位移时间曲线

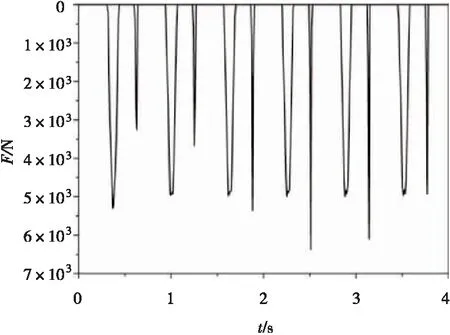
图10管脚左端碰撞力响应

图11管脚右端碰撞力响应

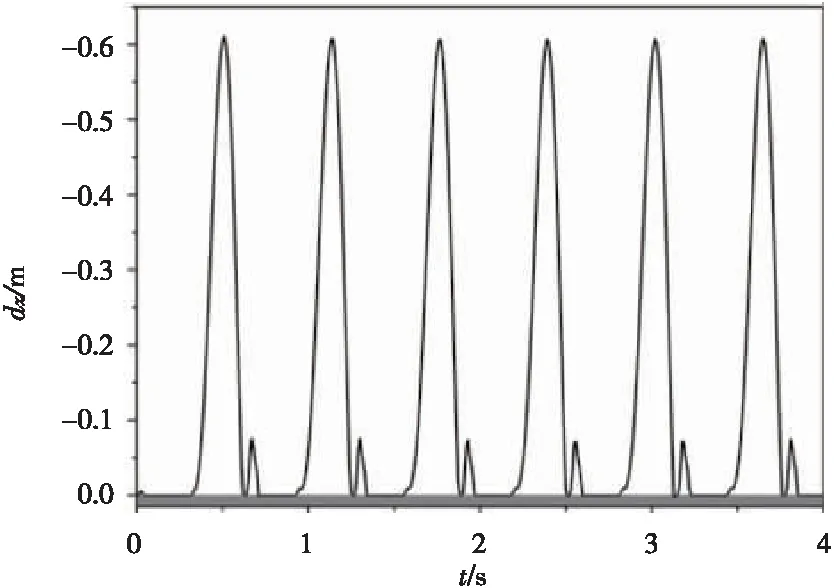
图12凸台处位移时间曲线

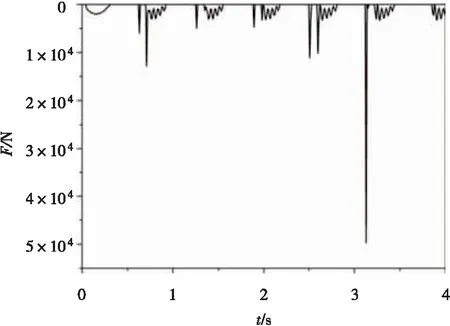
图13凸台处碰撞力响应

调整激励曲线幅值以分析管脚处左、右两端最大碰撞力的影响规律。管脚左、右两端最大碰撞力与激励幅值的关系分别如图14、图15所示。图14和图15中，随激励幅值(A)的增加，管脚左右两端的最大碰撞力(Fmax)呈增加的趋势。调整激励幅值以分析凸台处平均碰撞力的影响规律。凸台处平均碰撞力与激励幅值关系如图16所示。由图16可见，凸台处的平均碰撞力(Fave)随激励幅值(A)的增加呈增加的趋势。