土岩"二元基坑"吊脚桩支护体系锁脚锚杆预加轴力计算方法研究
2020-11-05杨红林
陈 诚,杨红林
(1.广州地铁设计研究院股份有限公司,广东 广州 510010;2.上海市隧道工程轨道交通设计研究院,上海 200292)
0 引言
随着城市化进程的加快、地下空间的开发利用,基坑工程迎来前所未有的发展机遇,但同时也遭遇到较多新的技术挑战,二元基坑的设计和施工就是其中之一[1-3]。二元基坑吊脚桩支护形式、受力机制、变形规律、适用范围仍是研究的热门课题[4-6]。
武军等[7]分析了土岩复合地层吊脚桩支护中土岩弹性模量比、吊脚桩嵌岩深度、岩肩宽度、桩体受力及变形之间的相关关系,指出当岩层弹性模量介于600 MPa和4 800 MPa之间时,最优设计嵌岩深度为1.5 m,最优设计岩肩宽度为1.5~2.0 m,但对支护体系的受力机制没有研究。陈勇[8]在吊脚桩支护设计计算方法中提出采用锁脚锚杆的预加力来抵抗桩脚受到的侧向水土压力,但没有说明锁脚锚杆预加力的具体计算方法。毕经东等[9]基于理正深基坑软件计算吊脚桩支护时,假定桩底嵌固长度取0.001 m,锁脚锚杆在开挖至锚杆上面1 m处施加,然后开挖至桩底,该计算中不考虑岩肩的嵌固作用,按照悬臂的受力状态计算,计算结果偏大,且计算过程与实际施工工序不一致,放大了锁脚锚杆的轴力。刘红军等[10-11]分析了二元基坑吊脚桩支护体系中桩体嵌固深度、桩脚处锚杆轴力和预留岩肩宽度对基坑变形的影响,指出锁脚锚杆对基坑稳定起绝对控制作用。李宁宁等[12]指出现场施工易造成岩肩岩体的破坏,施加一定的预应力能对控制围护体系的整体稳定起到较好的作用。赵文强[13]用理正深基坑计算吊脚桩支护体系时,基坑开挖至桩底,嵌固深度按0考虑,不考虑岩肩的作用。田海光[14]用plaxis软件对吊脚桩支护体系进行数值计算,得出吊脚桩预应力锁脚锚杆对控制桩底水平位移起到了较大作用。刘红军等[15]通过分析现场监测数据,认为设置锁脚锚杆能够有效地控制变形;并通过数值分析,指出基坑开挖和锚杆预应力大小是影响桩体深层水平位移以及桩体弯矩、剪力的主要要素。
综上所述,在吊脚桩支护体系中,锁脚锚杆预应力起着十分重要的作用,但目前的研究中对锁脚锚杆预加轴力的计算方法可以总结为2类:一种不考虑岩肩的作用,将岩肩处的水土作用力反向以预加力的形式加在锁脚锚杆上,这种做法偏保守,同时过大的预加轴力会造成桩身负弯矩偏大,造成配筋的浪费;另一种以试加预应力的方式,直到基坑变形得到控制为止,这种做法主观性较强。本文通过分析岩肩处吊脚桩与岩肩的相互作用,给出锁脚锚杆预加轴力的计算公式,以期指导吊脚桩支护设计。
1 吊脚桩锁脚锚杆预加轴力计算分析方法
1.1 吊脚桩与岩肩相互作用受力分析及计算模型
岩质边坡开挖后,土层基坑的支护桩(即吊脚桩)相当于岩质边坡的抗滑桩。吊脚桩与岩肩相互作用模型可简化为如图1所示的计算简图。图1中,作用在边坡潜在滑动面以下部分吊脚桩为锚固段,作用在滑动面以上部分吊脚桩为受荷段,阴影范围为抗滑桩桩后边坡的滑体。根据图1所示的计算简图,以桩前滑块为研究对象,得出岩肩与吊脚桩之间相互作用受力分析示意图,如图2所示。图2中,Tf为滑块潜在滑动面上的静摩擦力,F为岩肩抗力的反作用力,G为滑块的重力,N为作用在滑动面上的压力的反作用力,β为岩质边坡的破裂角,θ为岩质边坡的坡脚,H为岩质边坡的开挖深度,L为岩肩的宽度,h为吊脚桩的受荷段。
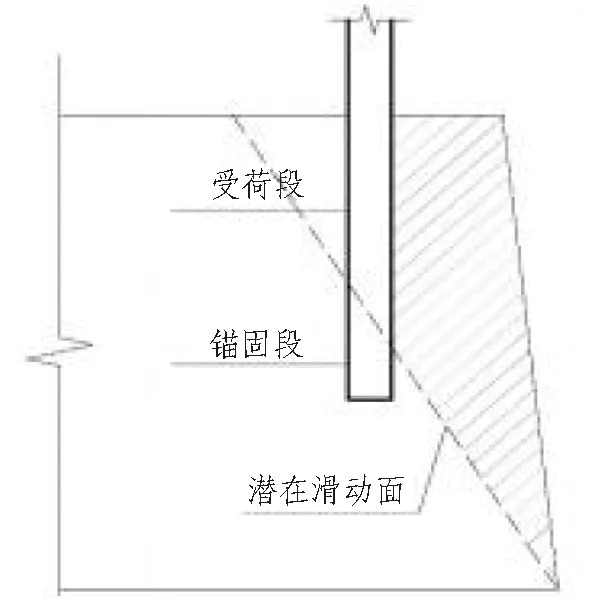
图1 吊脚桩与岩肩计算简图1Fig.1 Calculation sketch 1 of end-suspended pile and rock shoulder
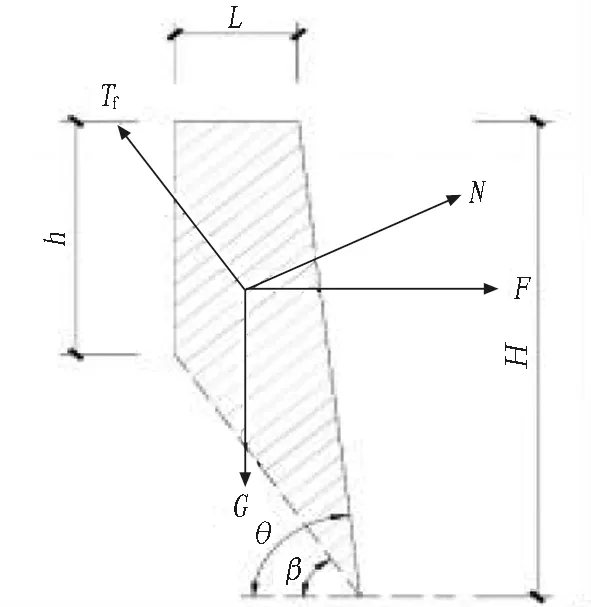
图2 桩前滑块受力示意图1Fig.2 Force sketch 1 of slider in front of pile
当岩质边坡开挖超过一定深度后,吊脚桩桩底位于滑块内,此时下滑的滑块对桩身产生一个推力。吊脚桩与岩肩相互作用可简化成如图3所示的计算简图2;滑块受力如图4所示,图中F′为滑块对吊脚桩推力的反作用力。
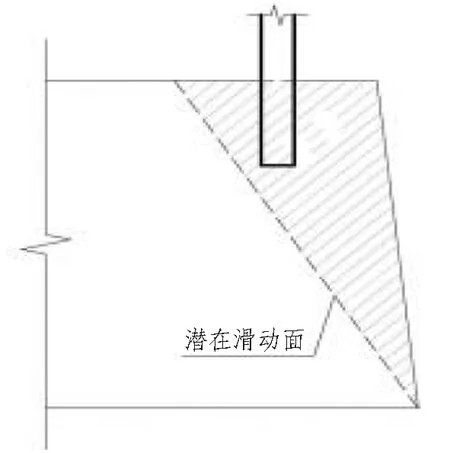
图3 吊脚桩与岩肩计算简图2Fig.3 Calculation sketch 2 of end-suspended pile and rock shoulder
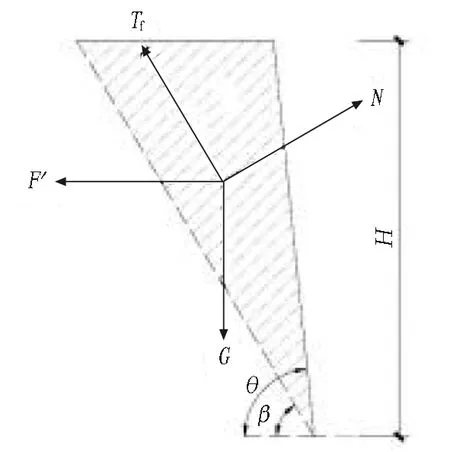
图4 滑块受力示意图2Fig.4 Force sketch 2 of slider
1.2 锁脚锚杆预加轴力计算方法
由图2可知,当吊脚桩位于潜在滑动面以下位置时,假定桩前滑体沿着潜在滑动面进行滑动,以潜在滑动面为横轴,作用在滑动面上的压力所在轴线为竖轴,建立平衡方程见式(1)。
(1)
式中:T为滑动沿滑动面的最大抗剪力;Fs为边坡稳定的安全系数。
据前文所述,锁脚锚杆的预加轴力等于岩层基坑未开挖时的被动区合力减去岩肩能提供的反力,得出:
(2)
式中:Fy为锁脚锚杆预加轴力;Fp为被动区土压力合力;ψ为锚杆与水平方向夹角。
根据几何相对关系,得出:
(3)
(4)
式(3)-(4)中:γ为土的重度;V为滑体的体积;l为滑体在滑动面上的长度。
当边坡失稳,滑块滑动瞬间,Tf、F均为0,此时:

(5)
式中:c为土体的黏聚力;φ为内摩擦角。
整理式(2)得:
(6)
由图4可知,当吊脚桩位于潜在滑动面以上位置时,滑块产生对吊脚桩的推力,建立平衡方程见式(7)。
(7)
此种工况下,滑块对吊脚桩产生一个水平的推力,此时锁脚锚杆的预加轴力应平衡滑块对吊脚桩嵌固段的推力F′,以及岩层基坑未开挖前被动区的土压力合力Fp,得出:
(8)
根据几何相对关系,得出:
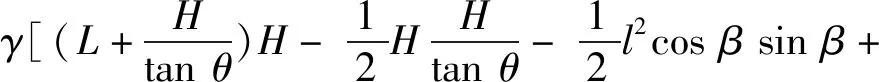
(9)
整理式(7),得出:
(10)
2 工程案例计算
2.1 工程案例
济南地铁某基坑采用吊脚桩支护体系,设计支护方案如图5所示。围护桩采用φ900 mm@1 300 mm,竖向设置3道锚杆(锚杆参数见表1),岩肩宽度为1.0 m,吊脚桩嵌固深度为3 m,勘察水位在车站底板以下。算例验证过程中,为简化计算,将土层、岩层分别简化为均一地层,具体取值见表2。
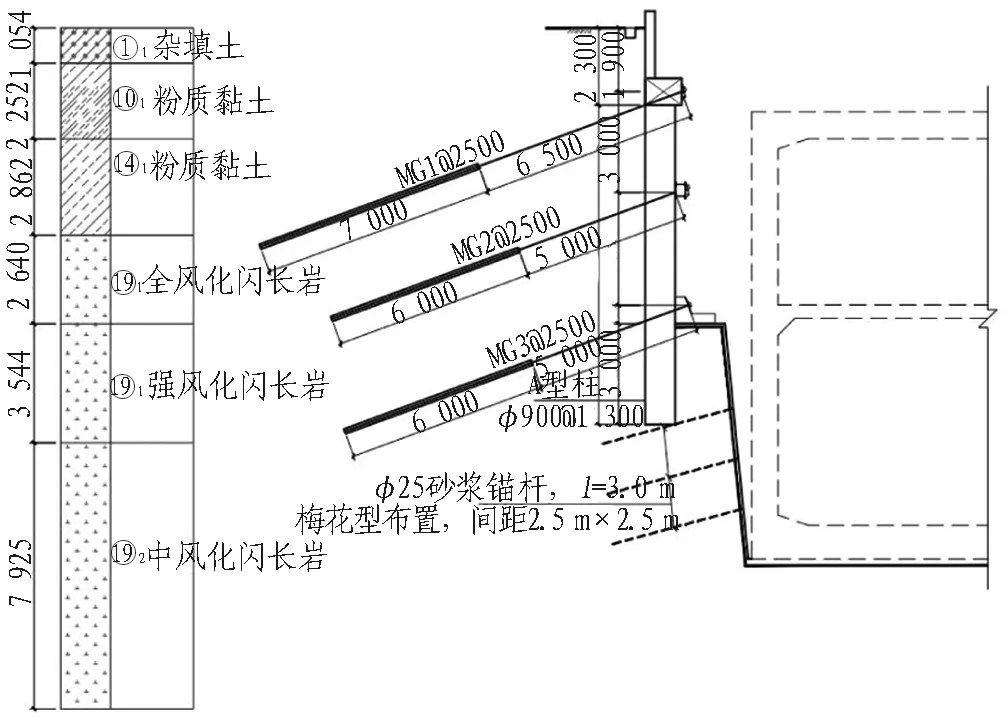
图5 吊脚桩基坑支护设计图(单位:mm)Fig.5 Design sketch of end-suspended pile support (unit:mm)
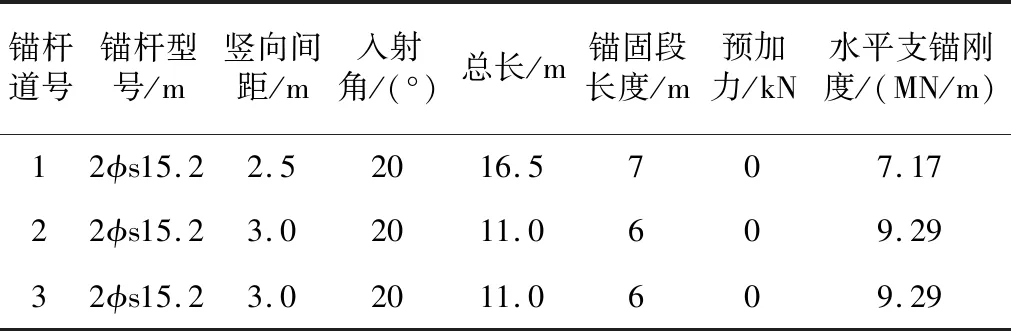
表1 支护结构参数表Table 1 Support structure parameters
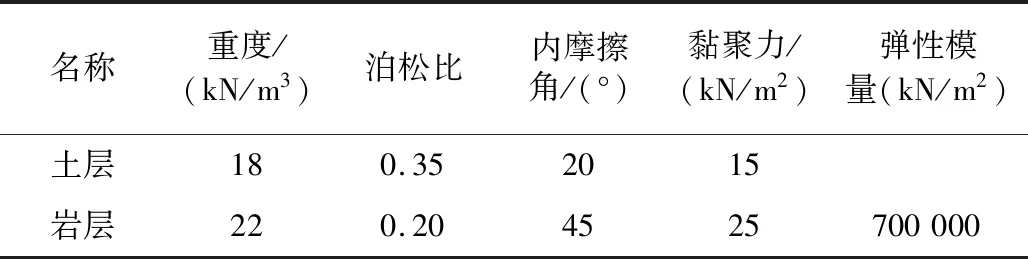
表2 地层物理力学参数表Table 2 Physico-mechanics parameters of stratum
2.2 数值建模
根据算例,建立模型如图6所示。模型的高度约取基坑开挖深度的3倍,边界约取开挖深度的2倍。地铁车站基坑通常为狭长型基坑,取二维横断面,按照平面应变计算;因基坑的对称性,取模型的一半进行计算,模型左右边界约束水平向位移,底边界添加固定约束。计算过程中,地层采用理想弹塑性模型,破坏准则采用摩尔-库仑屈服准则。
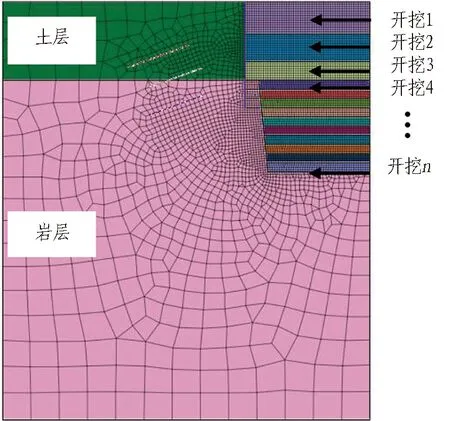
图6 计算模型Fig.6 Calculation model
围护桩、锚杆均视为连续、均质、各向同性体,采用弹性模型模拟,锚杆自由段采用桁架单元,锚固段采用梁单元;假定基坑每次开挖立即进行支护,稳定后执行下一次开挖;为进行数值试验,岩层的开挖步序按照每挖深1 m设置1个开挖步。计算过程中,对每一分析步进行强度折减,得出岩层边坡开挖过程中的边坡安全系数;不考虑锁脚锚杆的预加轴力。
2.3 数值计算结果分析
开挖到土层基坑坑底,岩层基坑按照每m开挖深度的步距进行计算,结果如图7-14所示。

图7 开挖步序4最大剪应变(Fs=4.39)Fig.7 Maximum shear strain of excavation step 4(Fs=4.39)
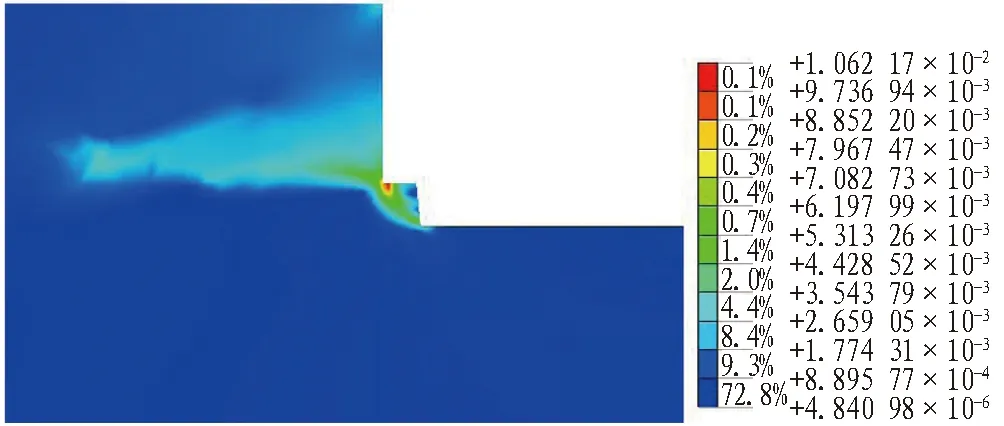
图8 开挖步序5最大剪应变(Fs=3.53)Fig.8 Maximum shear strain of excavation step 5(Fs=3.53)
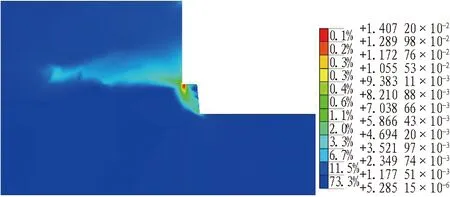
图9 开挖步序6最大剪应变(Fs=2.5)Fig.9 Maximum shear strain of excavation step 6(Fs=2.5)
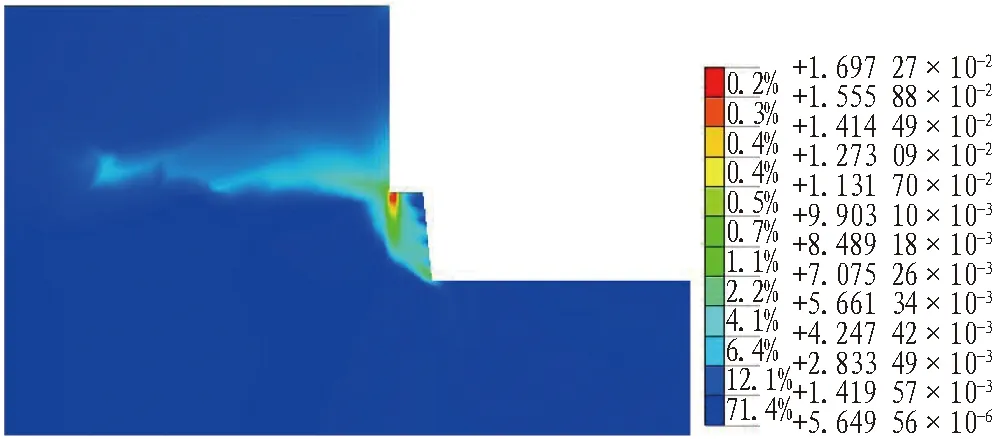
图10 开挖步序7最大剪应变(Fs=1.9)Fig.10 Maximum shear strain of excavation step 7(Fs=1.9)

图11 开挖步序8最大剪应变(Fs=1.6)Fig.11 Maximum shear strain of excavation step 8(Fs=1.6)
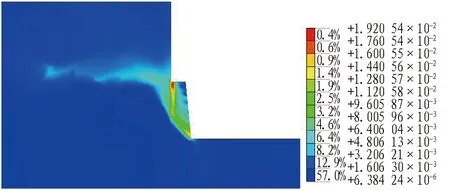
图12 开挖步序9 最大剪应变(Fs=1.4)Fig.12 Maximum shear strain of excavation step 9(Fs=1.4)
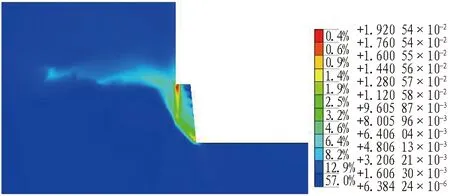
图13 开挖步序10最大剪应变(Fs=1.29)Fig.13 Maximum shear strain of excavation step 10(Fs=1.29)
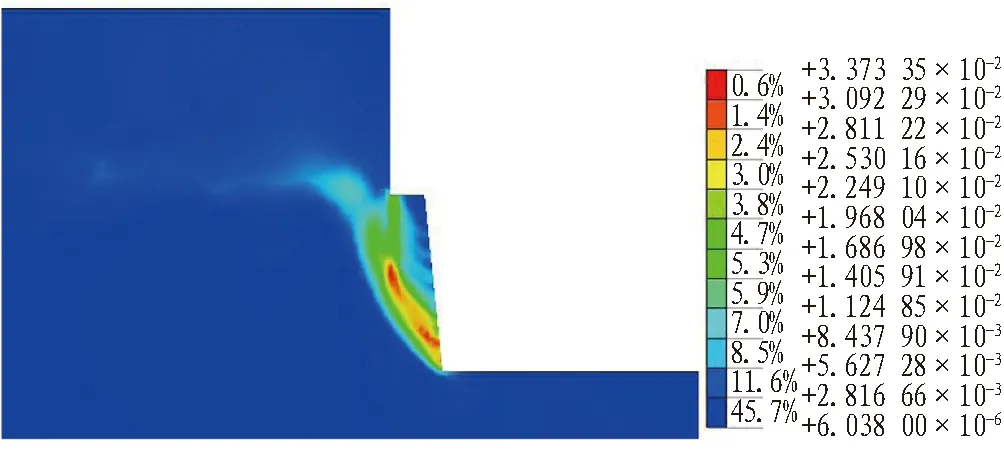
图14 开挖步序11最大剪应变(Fs=1.22)Fig.14 Maximum shear strain of excavation step11(Fs=1.22)
由图7-14可知:1)开挖到土岩交界面处,土体塑性区位于土层基坑的下部,最大剪应变位于岩肩处;2)随着岩层基坑的开挖,塑性区逐渐往岩质边坡移动,此时围护桩对岩质边坡起到了抗滑桩的作用,桩前岩层逐渐形成沿着潜在滑动面的塑性区;3)基坑开挖超过一定深度后,边坡产生了绕桩滑动的模式,开挖步序10时,最大剪应变位置由岩肩移动到坡脚,并沿着桩底和坡脚形成连续的塑性贯通区。
3 比较分析
根据式(2)、式(8)分别计算开挖4-11步序下岩肩反力,结果如表3和表4所示。
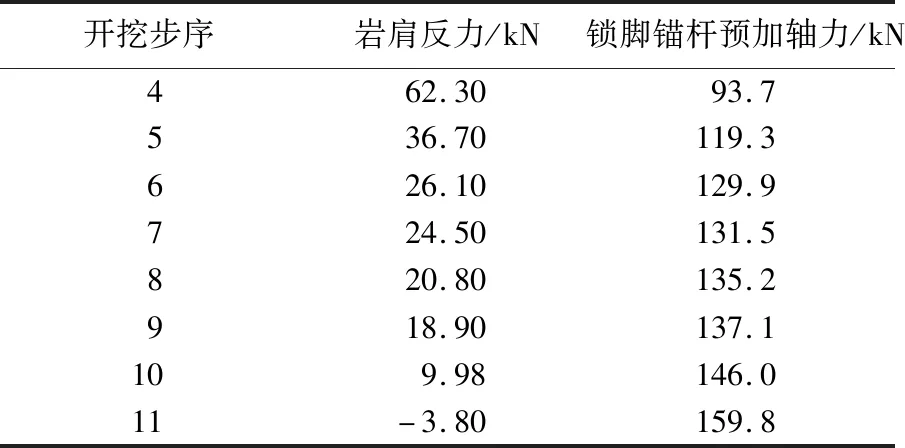
表3 不同开挖步序下岩肩反力(基于式(2))Table 3 Rock shoulder reaction forces in different excavation steps based on Formula 2
由表3可知:随着岩层基坑的开挖,岩肩能提供的反力逐渐减少,当开挖到步序11时,岩肩反力为负值。由表4可知:随着岩层基坑的开挖,滑块对吊脚桩的推力由负值到正值,当开挖到步序11时,推力值达到最大。计算结果表明,随着岩层基坑的开挖,岩肩的抗力逐渐减少,开挖到一定深度后,岩肩的抗力丧失,岩肩潜在的滑块对吊脚桩产生下滑的推力。该结果与1.1节的吊脚桩与岩肩相互作用受力分析及计算模型基本相符。为进一步验算计算公式的准确性,分别将表3和表4中的计算结果以预加轴力的形式加在锁脚锚杆上,对比桩身位移变化,整理出结果如图15-22所示。
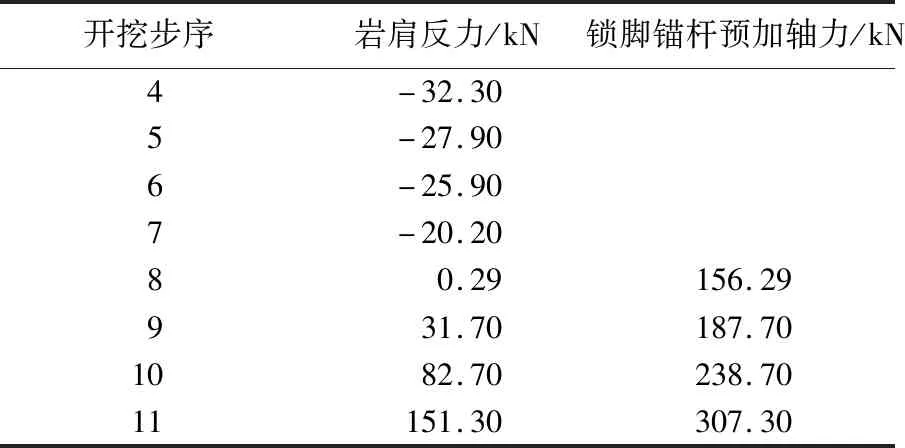
表4 不同开挖步序下岩肩反力(基于式(8))Table 4 Rock shoulder reaction forces in different excavation steps based on Formula 8
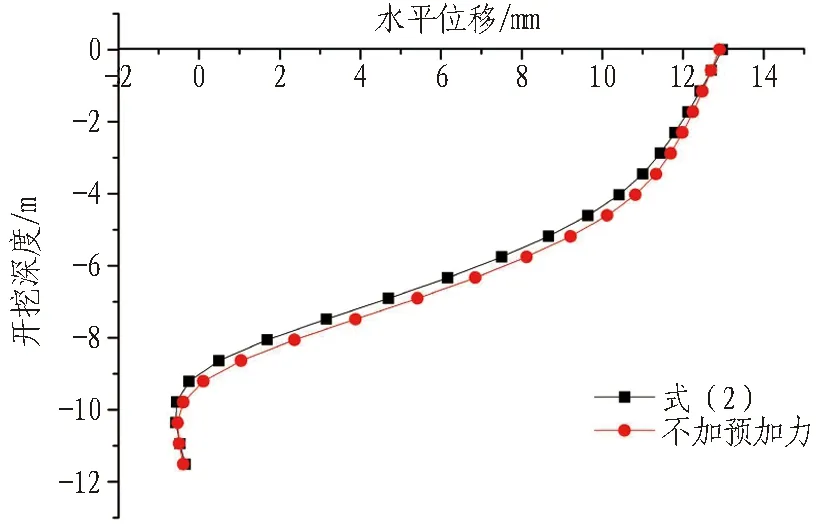
图15 开挖步序4位移曲线图Fig.15 Displacement curves of excavation step 4
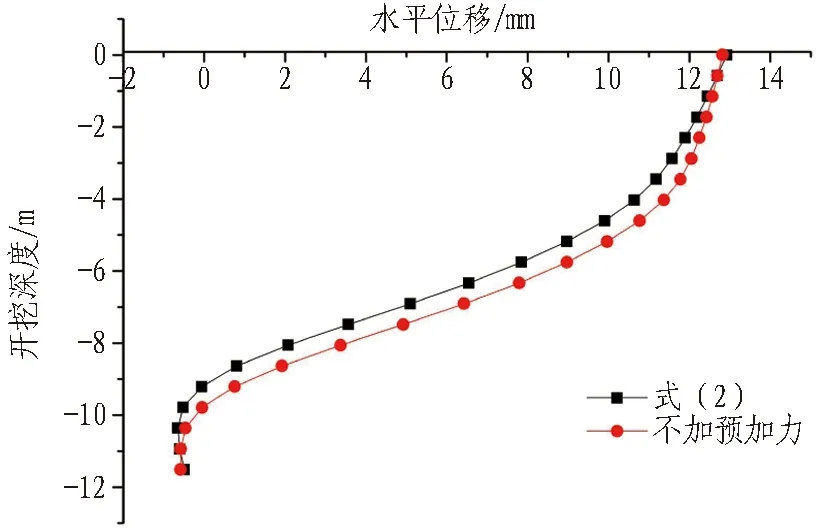
图16 开挖步序5工况对比图Fig.16 Displacement curves of excavation step 5
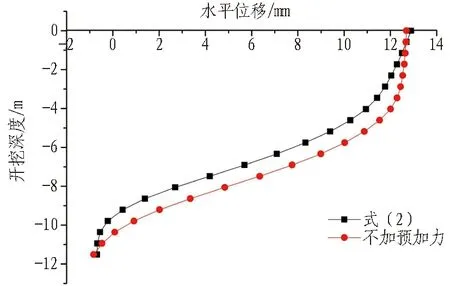
图17 开挖步序6工况对比图Fig.17 Displacement curves of excavation step 6
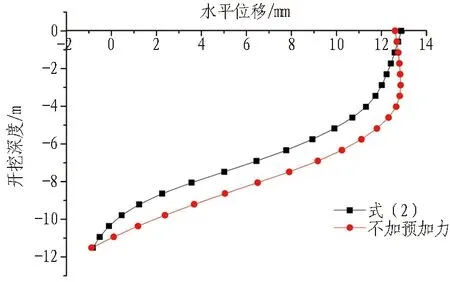
图18 开挖步序7工况对比图Fig.18 Displacement curves of excavation step 7
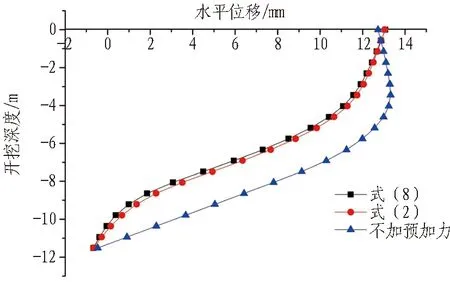
图19 开挖步序8工况对比图Fig.19 Displacement curves of excavation step 8

图20 开挖步序9工况对比图Fig.20 Displacement curves of excavation step 9
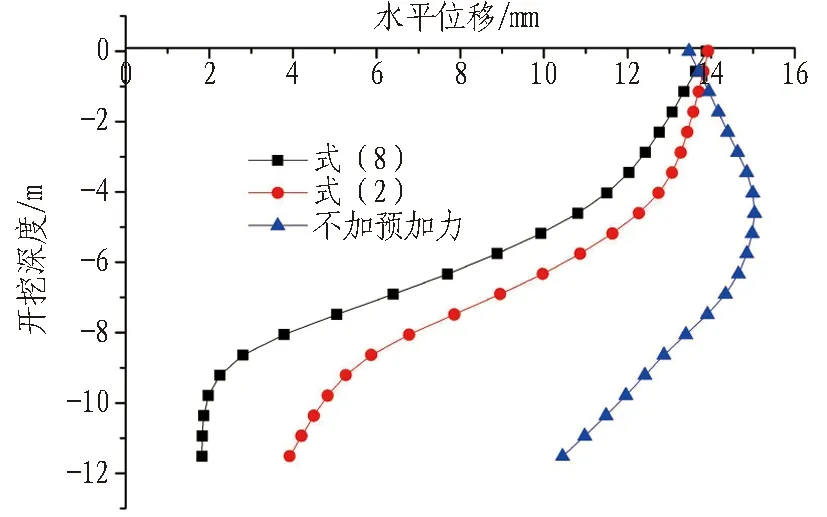
图21 开挖步序10工况对比图Fig.21 Displacement curves of excavation step 10
由图15-18可知:1)开挖步序4-7中,据式(2)计算得出的预加轴力能够有效地控制桩身位移;2)步序8中,式(2)与式(8)对桩身位移的控制效果接近;3)步序9开始,据式(2)计算得出的结果偏小,对桩身的位移控制效果不显著。
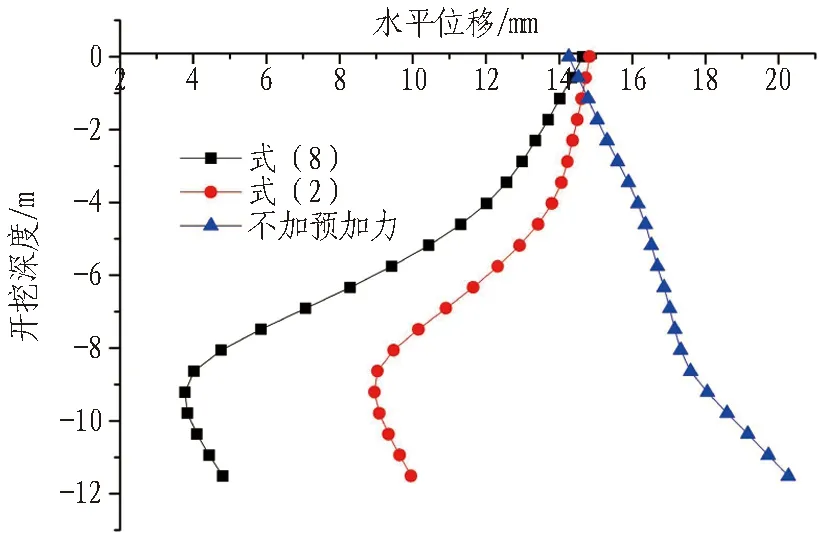
图22 开挖步序11工况对比图Fig.22 Displacement curves of excavation step 11
根据数值分析结果可知,式(2)需要吊脚桩在潜在滑动面下一定锚固长度的前提下才能适用。在步序9中,岩层开挖深度为6 m,对应的吊脚桩锚固段长度为0.86 m。因此,给出公式的适用范围如下:
(11)
式中Lcr为吊脚桩在潜在滑动以下的锚固长度。
4 结论与讨论

本文在讨论岩质边坡稳定性时,没有考虑岩层节理裂隙发育、结构面的产状等因素,因此存在一定的适用限制。在后续的研究中,应结合岩层的节理裂隙、结构面强度分析这些因素对吊脚桩受力体系的影响,同时根据工程案例的变形监测数据,进一步验证本文研究结果的合理性。
