基于地下水生态平衡埋深的隧道排水量设计计算
2020-11-05肖泽荣
肖泽荣
(福州市规划设计研究院,福建 福州 350108)
0 引言
随着经济发展及各地区交通设施改善,大型隧道建设逐年增加,不仅带来了新的交通发展和经济增长的机会,同时也给当地生态、水文和地质环境带来了挑战[1-5]。在富水地区隧道开挖和运营过程中,若隧道不采取任何限排措施,地下水将持续通过隧道渗漏,导致地表蓄水减少,甚至地表泉水干涸[2,6]。重庆中梁山隧道施工造成29处地表塌陷,48处泉水干涸,地表水影响面积约7.2 km2,严重危害当地居民的生产生活用水[7]。同时,地表水和地下水的减少导致了当地生态系统的缺水,造成了植物生长环境的恶化。宁夏六盘山隧道地下水漏失使榛子+箭竹群落的优势种(榛子和箭竹)的重要值下降明显,二者的生态适应能力有所下降[8]。因此,隧道排水量控制问题的研究十分必要。
之所以会出现隧道排水对环境的不利影响,是因为过去富水区隧道的防排水措施主要是“以排为主”,以减少水压对衬砌结构稳定性的影响[9-10]及控制施工成本。当隧道周边通过降雨、地下径流、渠道或河道渗漏等多种途径及时补充地下水时,隧道上方地下水位会逐渐恢复;当隧道周边仅靠降雨补充地下水时,地下水位可能持续下降,此时出于环境保护的角度,“以堵为主,限量排放”的指导思想将应用于工程实践[11-13]。“限量排放”是一个量的概念,国外挪威Oslofjord隧道的允许排水量是根据排水能力和经济效益确定的,居住和休闲区域的最大允许排水量为0.288 m3/(m·d)[14];挪威Baneheia隧道考虑城市休闲区对地下水排水的敏感性,其最大允许排水量为0.030 24 m3/(m·d)[14]。国内歌乐山隧道为保护水环境和植被,最大允许排水为1.0 m3/(m·d)[15];为了减少齐岳山隧道周边地表水的损失,根据工程地质条件、水文条件和设备的排水能力,确定其最大允许排水量为3.0 m3/(m·d)[12];程盼[16]、陈海帆[17]基于地下水生态平衡,考虑植被需水要求建立了一套确定隧道排水量的方法。目前已有隧道排水量研究的文献绝大部分还没有较为统一的计算方法和适用范围较广的极限标准规定,以往的隧道排水量规定在使用功能和地质环境方面都有自己的考虑和具体规定。程盼[16]、陈海帆[17]的研究虽然提出了隧道排水量的计算方法,但是忽略了植被水分胁迫的时间效应,本文在此基础上考虑水分胁迫时间提出一套隧道排水量设计方法。
本文首先利用地下水动力学中的面井法,建立隧道排水条件下的地下水渗流模型;然后,在考虑达到地下水生态平衡埋深时间t1及之后植物的水分胁迫时间t2时间段内地下水总排放量Qt与以降雨入渗补给为主的总补给量W的平衡分析,最终提出保持地下水平衡的排水量计算方法;最后,以福州某在建公路隧道为例,确定其极限排水量。研究结论以期为山岭隧道排水量的控制提供一定参考。
1 植被与地下水关系
1.1 地下水生态平衡埋深
地下水为植物提供水、盐、有机营养和热量。当地下水位下降到一定程度时,根系无法从毛细带吸收足够的水分,导致植被退化;如果长期缺水,植被就会消失;当地下水位过于浅时,会引起土壤盐渍化,威胁植被生长。根据这一现象,提出了地下水生态平衡埋深的概念,即地下水位满足植物正常生长,无灌溉情况下不会出现植被退化、土地荒漠化和土壤盐渍化等问题[18]。
天然植被生长与土壤含水率关系密切,在干旱区土壤含水率与地下水位埋深存在如下关系(具体数据见表1)[19]:
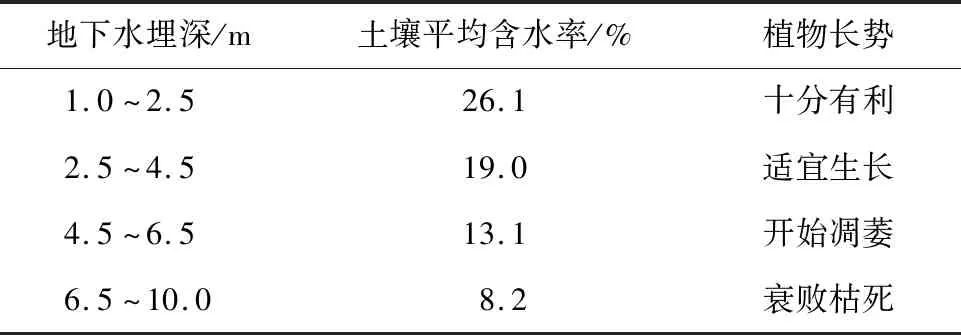
表1 土壤含水率与地下水埋深关系[19]Table 1 Relationship between soil moisture content and groundwater table[19]
θ=35.726exp(-0.185H)。
(1)
式中:θ为土壤剖面平均含水率,%;H地下水埋深,m。
由表1可知,适宜植被生长的地下水埋深不宜超过4.5 m。当然,不同地区由于气候、土壤等因素不同,同一植物在不同地区,其适宜生长的地下水埋深可能不同。
由于植被与地下水位密切相关,因此在确定隧道排水量时,有必要引入地下水的生态平衡埋深。隧道排水引起的地下水位下降必须保证不超过地下水的生态平衡埋深,以保护隧道场地的植被不受破坏。
1.2 地下水动态变化与植被长势关系
在隧道开挖、煤层开采时,难以避免会导致地下水位下降,植被短时间内随着地下水埋深增大不会产生枯萎现象。若地下水埋深长时间恢复不到地下水生态埋深,植物失水大于吸水时,细胞和组织紧张度下降,植物正常生理功能受到干扰,这种状态称为水分胁迫。植被对地下水位变化响应过程如图1所示[20]。

(a) 地下水位变化 (b) 植被响应图1 植被对地下水位变化响应过程Fig.1 Process of vegetation response to change of groundwater level
由图1可知,地下水位达到平衡埋深后,植物由天然平衡状态到植物生长减缓的几周时间内,如果大气降水补给量不小于隧道涌水导致的地下水漏失量,就能保证植被的正常生长。
2 隧道排水量计算方法
基于地下水生态平衡埋深,隧道排水量计算方法的具体过程如图2所示。
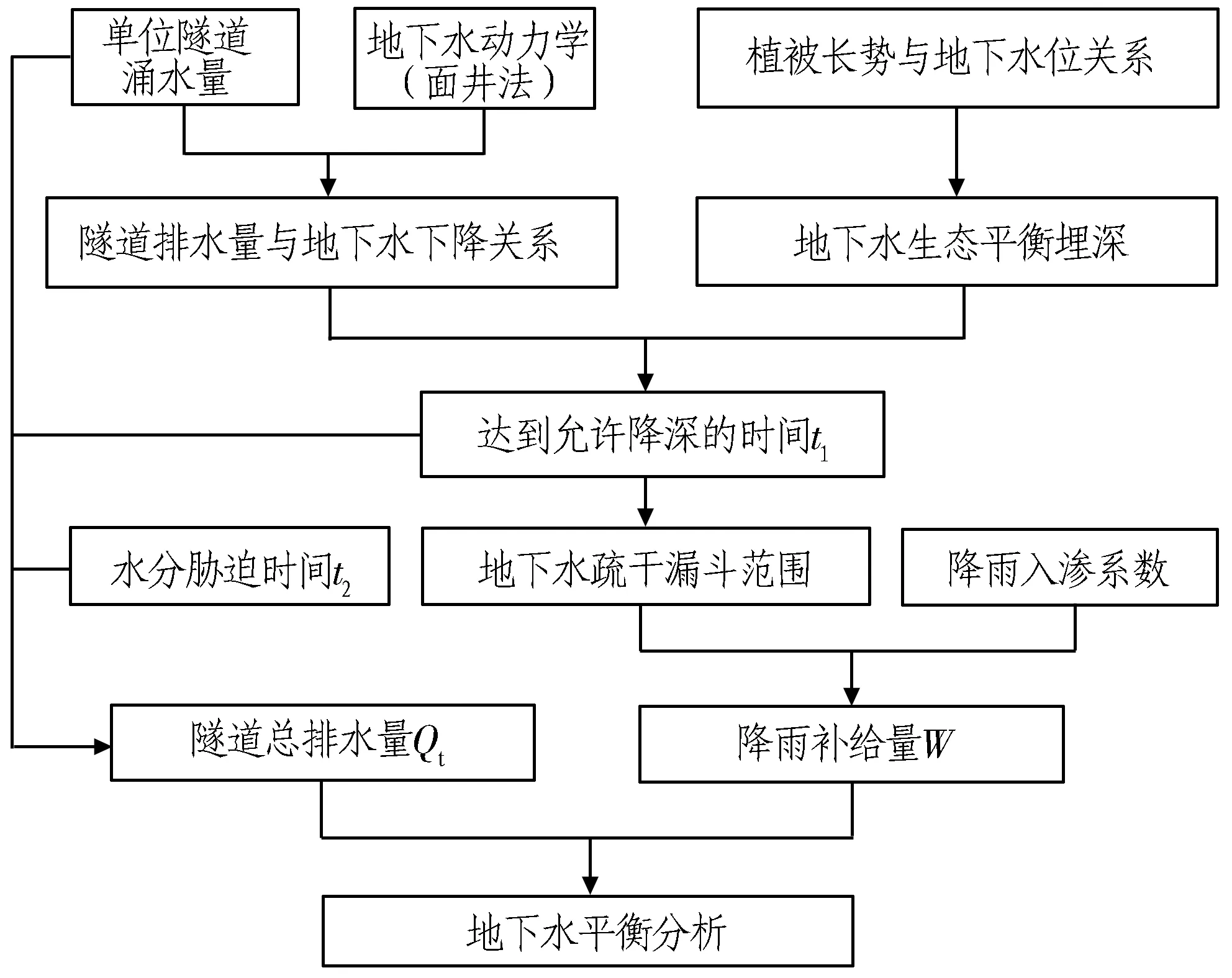
图2 隧道排水量计算方法的具体过程Fig.2 Specific progress of calculation method for tunnel drainage
2.1 隧道排水与地下水位下降的关系
由于隧道渗流与井抽水相似,目前隧道排水后地下水位降深的计算方法一般是基于地下水动力学中的井流理论,假设隧道壁由无限个抽水井组成,并考虑无限个抽水井的叠加[16-17],如图3所示。最终采用地下水动力学中的面井法[21]得到地下水降深计算方法。
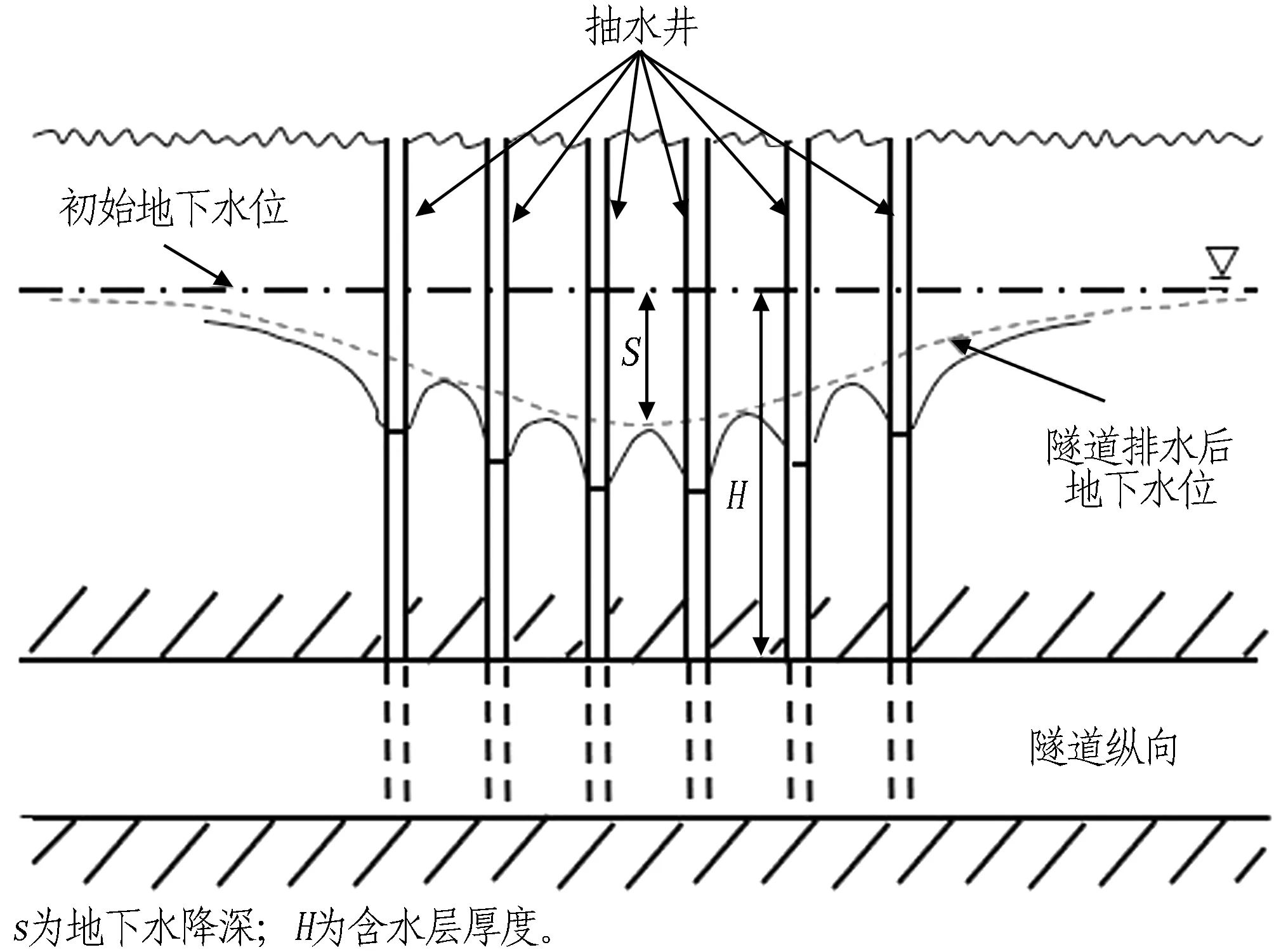
图3 隧道纵向抽水井示意图Fig.3 Sketch of pumping wells in longitudinal section of tunnel
地下水位降深的计算采用Theis公式[22]最为广泛,其基本方程如下:
(2)
(3)
(4)
式(2)—(4)中:s为降水影响范围内任意点水位降深,m;Q为隧道每天涌水量,m3/d;T为含水层导水系数,m2/d;a为压力传导系数,a=T/μ,μ为给水度;t为渗漏开始到计算时刻的时间;r为任意降深点到井的距离,m;W(u)为井函数。
隧道排水既不同于单点降水,也不同于多点降水,因此引入面井法来计算地下水位的降深。面井法(综合面状)即在某种几何形状(例如矩形和圆形)面积上井孔的流量分布比较均匀时,可以将井群视为一个整体,把从各个点井抽水的井群视为在井群分布面积上均匀“蒸发”的面积井,即通常所谓的汇面[21]。
采用面井法计算地下水降深时,首先假设:1)隧道截面为标准圆形,隧道整体为圆柱形。然而,隧道截面形状通常为马蹄形,需要根据面积等效原理转换成圆。2)隧道壁面涌水量均匀、稳定、处处相等。
令隧道长度为L,半径为R0,隧道轮廓如图4所示。当隧道墙面扩展成一个平面,平面尺寸L=2lx,宽度2πR0=2ly,如图5所示。假设平面是由无数微小的渗水面组成,则平面上的入渗量处处相等。微面对任意点M的作用可以看作是单井的作用,因此通过微元的作用积分可以得到整个面对M点的作用。
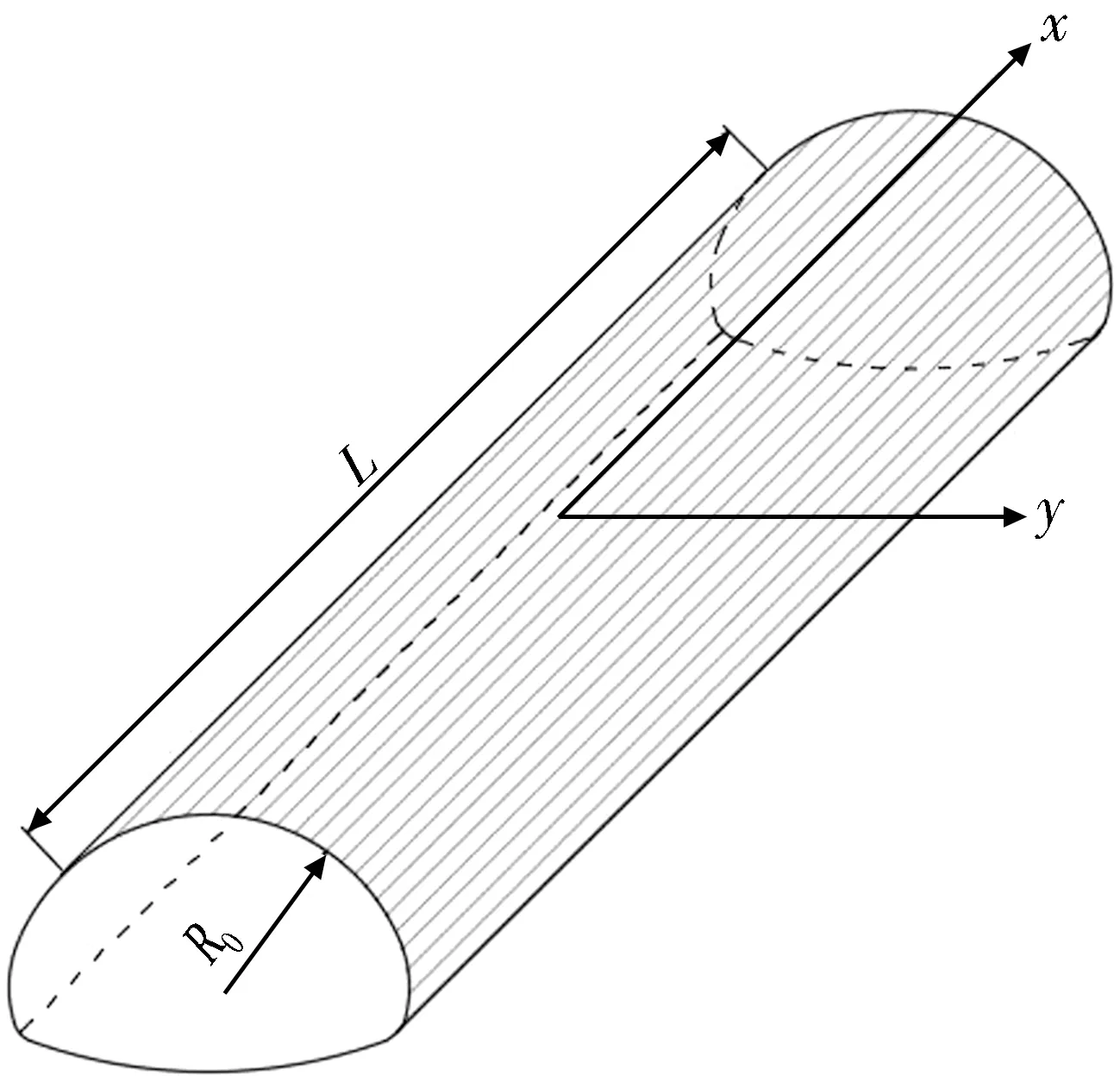
图4 隧道轮廓Fig.4 Tunnel profile
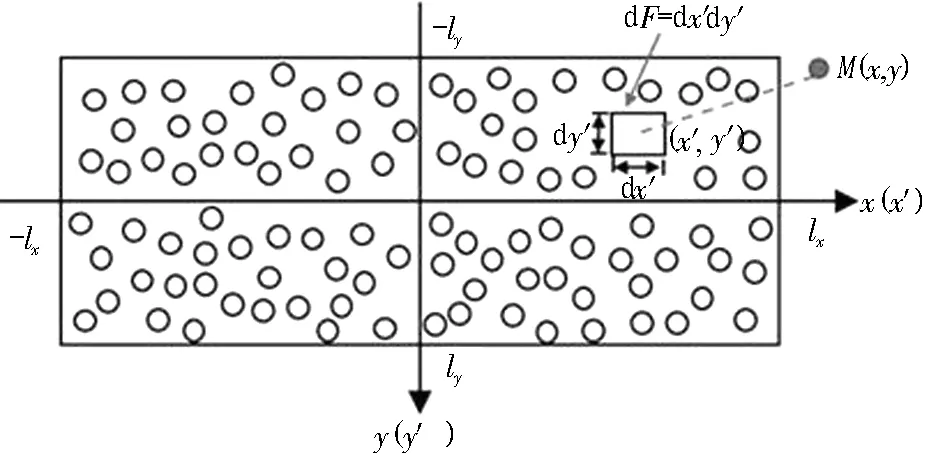
图5 面井示意图Fig.5 Sketch of area wells
假设隧道每延米涌水量为q,则汇面上单位时间涌水量Q为单位长度隧道涌水量q与隧道长度L的乘积,即:
Q=qL。
(5)
那么单位面积上的涌水量
(6)
坐标系的取法见图5。坐标系x′oy′用来表示开采段内微分汇面的位置,而坐标系xoy则用来表示拟计算降深点的位置。
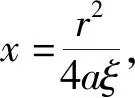
(7)
于是无限平面上在流量Q的汇点作用下,任意点降深
(8)
在汇面上以任意点(x′,y′)为中心取微分汇面dx′dy′,该汇面上的流量为εdx′dy′。点M(x,y)在微分汇面dx′dy′的作用下,其微分降深
整个汇面对M(x,y)的作用,可在整个开采面内积分得到,即
(10)
式(10)经过一系列数学换元计算,得到矩形面井下任意点M(x,y)任意时刻的降深方程:
(11)
其中,Ar可称为矩形面井的井函数:
(12)
式(12)中S*为定义函数:
(13)
式(13)中erf(v)为高斯误差函数:
(14)
函数S*(α,β)的值通过MATLAB编制计算得到。对于单洞隧道中心点,设式(11)中的x=0、y=0,则隧道中心点的地下水位降深
(15)
显然最大地下水位位于隧道中心处,式(15)为隧道排水引起的最大地下水位降深计算公式。
2.2 隧道排水影响范围
程盼等[23]指出隧道长时间排水后,由于隧道长度大于宽度,疏干漏斗呈现倒椭圆椎体,在地面形态上呈现椭圆形。地面上的椭圆面积即为隧道影响范围内降水入渗补给面积。
2.2.1 横向影响范围
在横向上(即隧道垂直方向),取降深为0的点作为影响范围的边界,令x=0、y=b,则:
(16)
当s=0时,此时求解出来的b,即为椭圆短半轴,即横向影响范围。
2.2.2 纵向影响范围
在纵向上(即隧道走向方向),取降深为0的点作为影响范围的边界,令x=l、y=0,则:
(17)
当s=0时,此时求解出来的l即为椭圆长半轴,即纵向影响范围。
已知椭圆长短轴半径后,则可得到椭圆面积F,即隧道影响范围内降水补给面积:
F=πlb。
(18)
2.3 隧道排水范围内降水补给
大气降水落在地面上,一部分蒸发、一部分形成地表径流、其余部分则入渗地下渗流补给地下水。对于山区隧道而言,补给源头以降水为主,通常采用降水入渗系数来确定降水补给量[24]:
W1=pWaF/365。
(19)
式中:W1为日均降水补给量,m3/d;p为降水入渗系数;Wa为年平均降水量,m;F为降水入渗补给面积,m3。
2.4 地下水平衡分析
在进行降深计算时,单位时间内每延米的排水量为q,则t时间内的总排放量
Qt=qLt=qL(t1+t2)。
(20)
式中:t1为允许到达降深的时间;t2为达到允许降深后水分胁迫时间。
同时,t时间内总补给量
W=W1t=W1(t1+t2)。
(21)
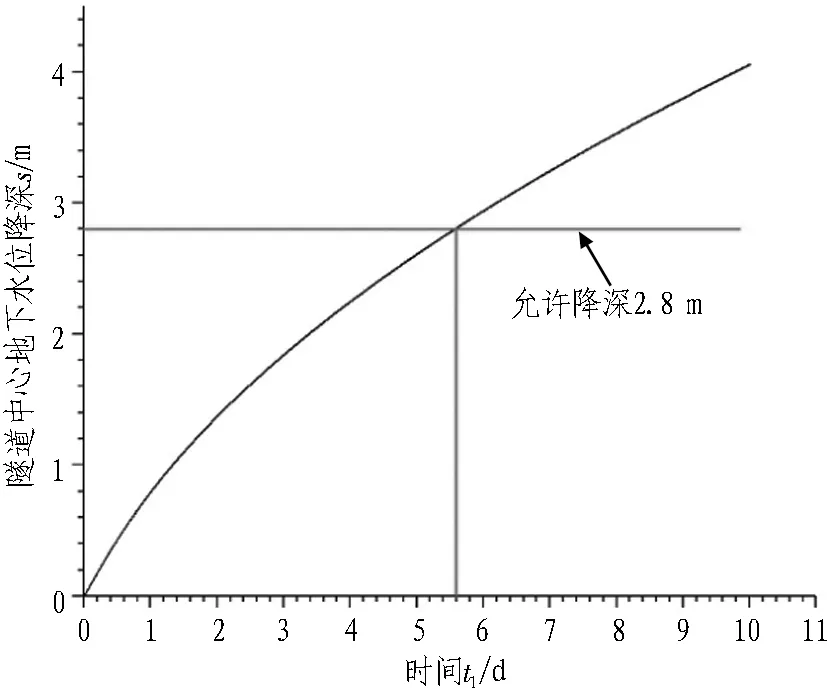
将Qt与W进行比较,若Qt=W,则地下水总量保持平衡;若Qt>W,则排水量过大,在此排水量下隧道地下水会被疏干,影响生态环境,应适当减小排水量;若Qt 福州市某在建公路隧道全长1 170 m,其中约L=1 000 m通过含水层。隧道最大宽度B=20.02 m,高13.53 m,等效圆半径R0=10.8 m;隧道场地围岩主要为不稳定全风化和中等风化花岗岩;地下含水层平均厚度H=30 m;围岩渗透系数取自本项目勘察阶段报告,综合取值为K=0.3 m/d;给水度根据常见岩石(土)给水度经验值按强、中等风化岩层取值μ=0.02;含水层的导水系数T=KH=9 m/d。福州地区月均降水量见表2,由表可知,福州年平均降水量为Wa=1 359 mm,考虑本地区实际情况10月、11月、12月、1月、2月为旱期,取这5个月降水量计算日均降水量更安全。该地区岩性较破碎,故取降雨入渗系数p=0.2[24]。 表2 福州地区月均降水量Table 2 Average monthly rainfall in Fuzhou 根据实地调查,隧道上方的主要植物有樟树、芒果树、龙眼树和榕树,其中樟树直径为0.3~0.9 m,芒果树直径为0.3~0.8 m,龙眼树直径为0.2~0.4 m,榕树直径为0.7~1.5 m。目前还没有针对这些树种地下水生态平衡埋深的研究。因此,综合考虑生态保护和建设成本并参考表1,暂时确定本项目地下水生态平衡埋深为4.5 m。据福州项目勘察设计报告,获得此项目地下水位为1.2~2.2 m,本研究取地下水平均埋深为1.7 m,因此允许降深s=4.5-1.7=2.8 m。 根据本项目勘察阶段报告,未进行堵水时隧道正常涌水量为543.77 m3/d,最大涌水量为1 882.91 m3/d,则每延米平均涌水量q=1.21 m3/(m·d)。 根据式(15)可得到隧道中心处降深s=2.8 m时的时间t1,通过MATLAB编程可得到地下水降深与时间t1的关系,如图6所示。由图可知,当t1=5.6 d时,地下水位降深为2.8 m。 图6 隧道中心处地下水降深与时间关系Fig.6 Relationship between groundwater drawdown and time in tunnel center 当t1=5.6 d时,式(11)中令x=0,可得隧道中心横断面地下水位降深如图7所示;当t1=5.6 d时,式(11)中令y=0,可得隧道中心纵断面地下水位降深如图8所示。为了更加直观地观察地下水疏干漏斗,采用MATLAB编程实现了地下疏干漏斗的三维图,如图9所示。由图7—9可知,离隧道中心处距离越近,此处地下水位降深越大。同时由图7和图8可分别得到隧道中心处横向影响范围、纵向影响范围为-210~210 m、-650~650 m。 图7 隧道中心横断面处地下水位降深Fig.7 Groundwater drawdown in cross-section of tunnel center 图8 隧道中心纵断面处地下水位降深Fig.8 Groundwater drawdown in longitudinal section of tunnel center 图9 地下水降深三维示意图Fig.9 Three-dimensional diagram of groundwater draw down 当t1=5.6 d时,式(16)、式(17)分别可以得到地表疏干漏斗的短、长轴b=210 m、l=650 m,此处b、l的计算精度为0.01。已知b、l后,则可得到降水补给面积F=πbl=428 827 m3。 在式(19)基础上改进,则可得到旱期10月、11月、12月、1月、2月的日均降水补给量WD=pFW旱/150=0.2×428 827×0.247/150=141.23 m3/d。 植物由天然平衡状态到植物生长减缓的时间为t2,t2由图1可知一般为几周内。由于不同植物对地下水变化的响应时间不一致,考虑工程隧道上方榕树不耐旱,暂将t2取值为4周(28 d),因此t=t1+t2=33.6 d。 当t=33.6 d,总排放量Qt=qL(t1+t2)=40 656 m3,地下水补给量W=WD(t1+t2)=4 745.3 m3,可见地下水总排放量远大于雨水的补给量,长期排放会疏干地下水,破坏生态环境,因此需减小原始排水量q,达到地下水平衡。 由于在计算之前无法得到q的取值范围,应尽快使Qt等于W。如果取值范围太大,计算效率会很差,所以采用二分法来确定q值。具体步骤如下:1)先确定q的取值区间(0,1.21),取区间内的近似中值0.60进行试算,此时W-Qt= -14 982.8 m3<0;2)再次确定q的取值区间(0.60,0),取区间内的中值0.3进行试算,W-Qt=5 703.2 m3>0;3)再次确定q的取值区间(0.60,0.3),取区间内的近似中值0.45进行试算,W-Qt= -4 587.6 m3<0;4)再次确定q的取值范围(0.3,0.45),取区间中值0.375进行试算,W开始略大于Qt,故选取q=0.375 m3/(m·d)附近的值进行试算。当q=0.4 m3/(m·d)时,W-Qt=1 431.3 m3>0,且W接近Qt,能维持地下水平衡。为了反映q值与排水影响范围、降雨补充量W及隧道排水总量Qt的关系,再分别选取q值等于1和0.8进行计算,结果如表3、图10及图11所示。 表3 不同隧道排水量下计算参数值Table 3 Parameter values under different water inflow q 图10 q与隧道排水影响范围关系Fig.10 Relationship between q and influence scope 图11 q与隧道排水总量、降水总补给量关系Fig.11 Relationship between q and rainfall recharge W and tunnel discharge Qt 由图10和图11可知,在地下水生态平衡埋深已知,即地下水降深一定时,随着隧道单位排水量的增大,隧道上方影响范围逐渐减小,降水补给量逐渐减小,排放总量逐渐增加。补给量与隧道影响范围有关,隧道影响范围减小导致补给量减小;排水总量与单位排放量有关系,单位排放量增大,导致排放总量增加。由于补给量与排水总量一减一增,所以存在一个排放量使排水总量等于补给量。对于本工程案例,q=0.4 m3/(m·d)时,降水总补给量略微大于隧道排水总量,能维持地下水平衡。若参考程盼[16]、陈海帆[17]的排水量的算法,不考虑植物水分胁迫的时间效应,此时q=0.28 m3/(m·d),其值小于0.4 m3/(m·d),原因是忽略了地下水位达到生态平衡埋深时,植物不会马上枯萎,有一定耐受性,导致其计算结果偏保守。 通过引入生态学中地下水生态平衡埋深的概念及水分胁迫时间效应,基于地下水动力学方法,同时考虑降雨补给,建立了一套确定保护生态环境的隧道限排量的方法,得出以下结论: 1)从保护生态植被不受破坏的角度出发,采用地下水动力学中的面井法,推导出单孔隧道地下水排水量与地下水降深的关系。其目的是在植被正常生长所需要的范围内控制地下水的下降,维持隧道内植被的生态平衡。 2)采用面井法得到了隧道排水的渗流模型,并利用该方法计算了降深为0 m时隧道的影响范围,从而确定了降雨入渗补充的面积。根据降雨入渗系数,得到降雨入渗补给量W,并与地下水总流量Qt进行比较。通过不断调整单位排水量q使地下水总流量Qt与降雨入渗补充W相等。当它们相等时,q即为隧道保持生态平衡的地下水最大排放量。 3)以福州某在建的公路隧道为例,提出了该隧道保持地下水平衡的单位涌水量为q=0.4 m3/(m·d)。在分析过程中,为了更直观地展示地下水漏斗的形状,通过MATLAB编程对绘制了地下水位随时间变化的二维图和三维图。 4)在地下水生态平衡埋深一定时(即地下水降深一定时),随着隧道单位排水量的增大,隧道影响范围逐渐减小,降水补给量也逐渐减小,排放总量逐渐增加,所以存在一个单位排放量使排水总量等于降雨补给量。 5)未考虑水分胁迫时间效应得到的排水量较考虑水分胁迫时间得到的排水量偏于保守。 这套公式计算地下水降深时建立在隧道瞬间贯通、全长度全断面排水的条件下,主要适用于隧道运营期排水量的控制计算,假定施工期严格采取注浆堵水措施,未对地下水造成实质影响(理想状态);或者施工期间造成地下水下降,后期采取人为措施等短时间将水位恢复。隧道后期运营是一个长期过程,需要长远考虑保护植被生态环境,因此需采取限量排放措施。同时,本文提出的隧道限排量方法存在以下问题待研究:1)不同地区不同植被类型对应地下水生态平衡埋深存在差异,同时不同植被对缺水条件下水分胁迫时间也不一致;2)隧道排水的渗流模型中,假定地下水位水平,与实际的山岭隧道的地下水位存在差异;3)降水补给中未考虑坡面角度、高度等,与实际降水补给量存在一定差异。后续将针对上述因素专项研究,从而形成一套完整基于地下水生态平衡埋深的隧道排水量的计算方法。3 工程案例分析
3.1 工程背景
3.2 达到允许降深时间t1
3.3 地下水疏干漏斗形态
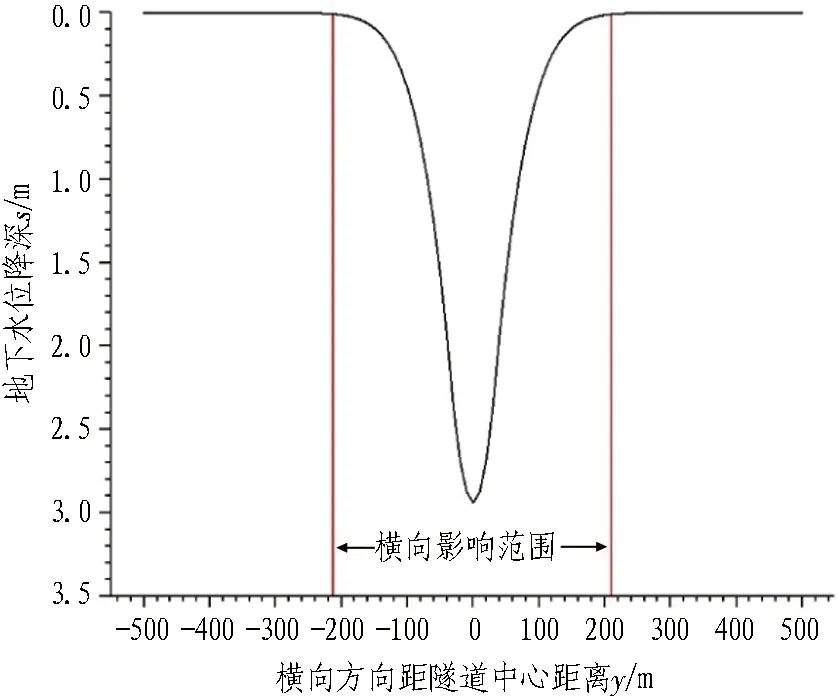
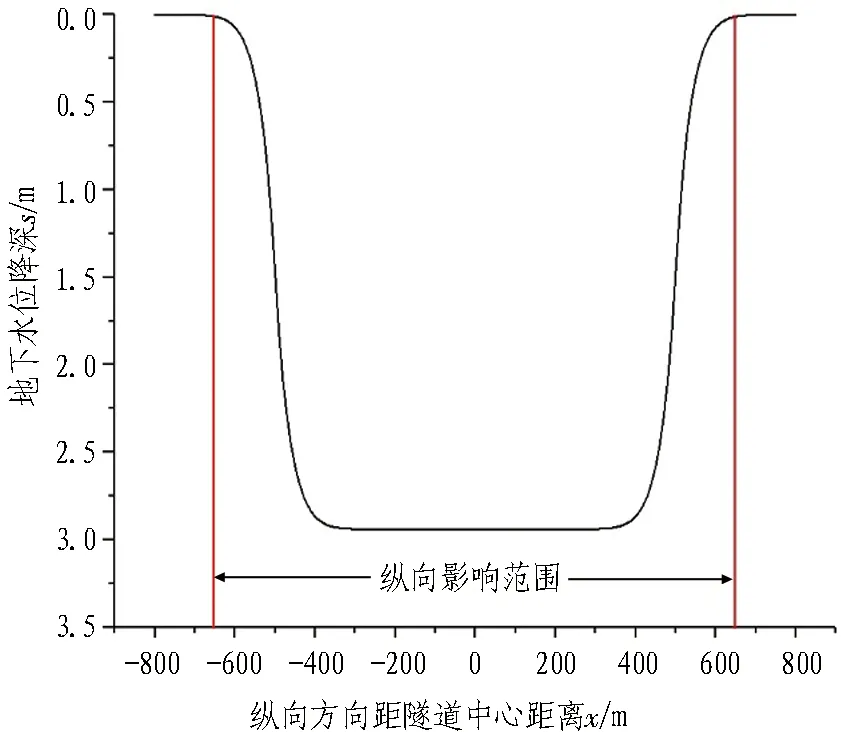
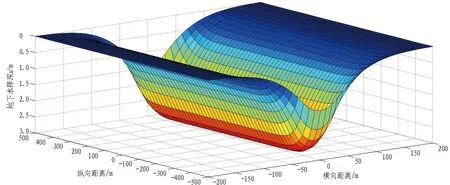
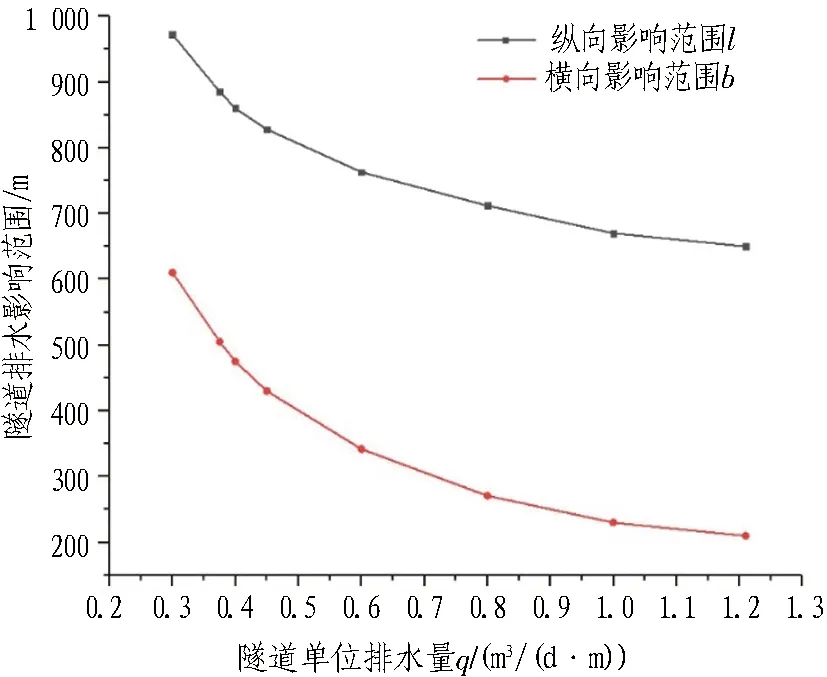
3.4 隧道排水影响范围及降水补给量确定
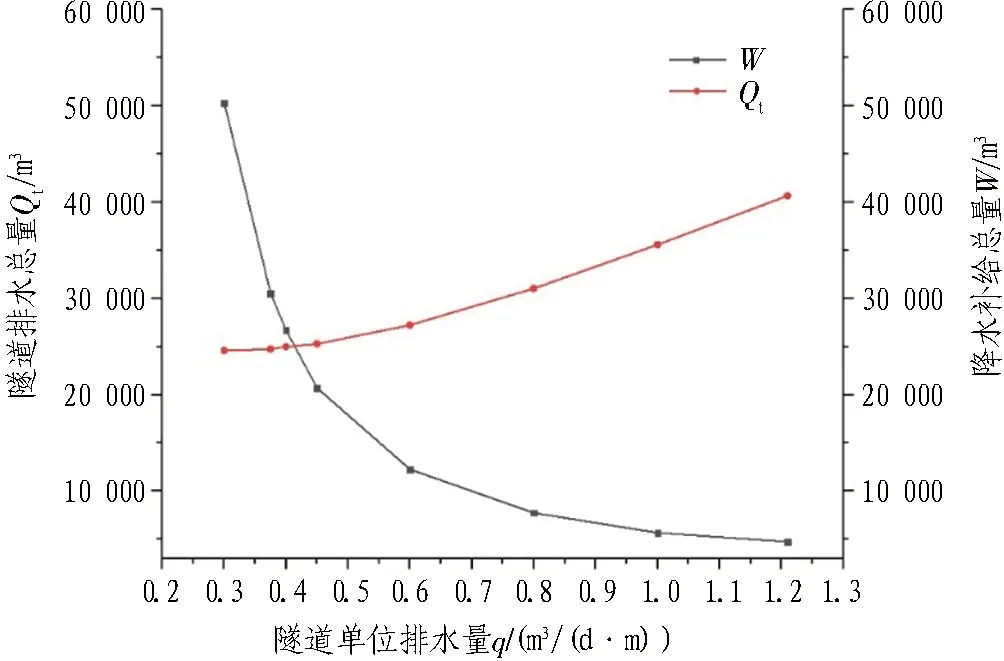
3.5 地下水平衡分析及维持地下水平衡排水量的确定
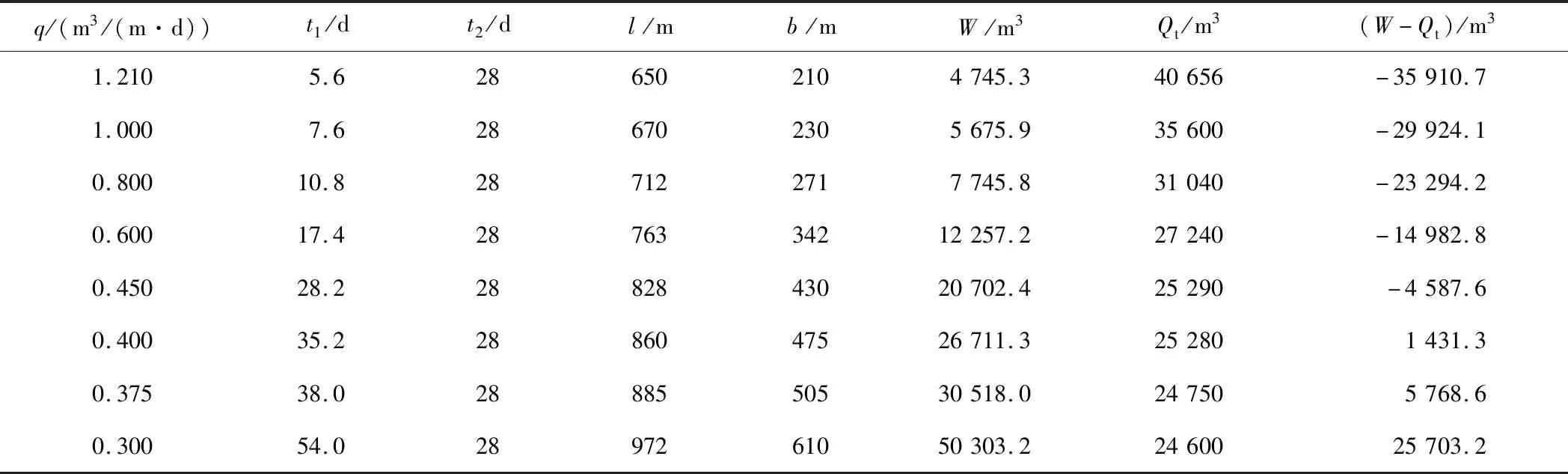
4 结论与建议
