在疑问中推进在活动中建构
——特级教师苏明杰《圆的认识》教学片断赏析
2020-11-05冯凯
冯凯
片断一:“摆圆”。
师:这里有一些小磁铁,苏老师想组织一个比赛,30秒钟用这些小磁铁在黑板上摆一个圆,看谁摆得又快又圆!
师:谁来评价一下这两位同学摆成的“圆”?
生:摆得都不圆,磁铁有的缩在里面,有的跑在外面。
师:缩在谁的里面,跑在谁的外面?
生:圆!
师:这是为什么呀?
生:时间紧、没工具。
师:如果延长时间,可以摆得怎么样?有没有能摆得一定很圆很圆的把握?难度在哪里?
生:时间延长了,可能要重复好多个回合,也许做无用功。把握不大,毕竟距离不好控制。
师:什么距离?
生:磁铁到中心的距离拿不准。
师:你怎么想到磁铁到中心的距离?
生:投沙包游戏就是站成圆形往中心投沙包的。
师:这位同学联系生活经验来思考,很会学习!如果老师再提供一些工具,你们能不能摆得更圆一点?(小棒、直尺、线)先请静心想一想,你打算怎样利用工具把它摆得更圆?这样做是为了达到什么样的目的?
生:小棒、直尺、线三种工具都可以用。工具不同,只要让所有的磁铁到中心的距离相等就摆得更圆了。
(学生上黑板用工具摆圆)
师:现在怎么样啦?
生:很圆了!
师:为了摆出的圆更圆,我们请电脑来帮忙,这样可以减少误差。(课件演示:圆的形成)
师:通过刚才的活动,你们知道怎样的点能围成圆了吗?
生:到中心距离相等的点就能围成一个圆。
师:对!那圆是什么?圆就是到一个中心距离都相等的点所围成的平面图形。这个中心点叫做圆心,这个相同的距离叫做半径。我们的祖先很早就发现这个奥秘了,古代思想家墨子是这样描述圆的:“圆,一中同长也”。谁能解释一下“一中同长”是什么意思?
生:一个中心,距离等长。
师:圆是一中同长,下面这些图形有没有一中同长呢?与这个点同长的有几个?现在呢?逐渐增加边数……
课件演示:
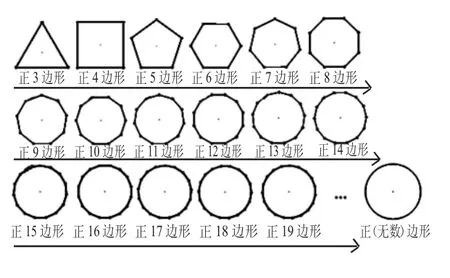
(学生依次回答出与中心点同长的有3个、4个、5个、6个、7个……无数个)
师:现在你对正多边形和圆又有什么样的理解?
生:正多边形越来越接近圆,圆是正无数边形演变来的。
师:通过刚才的研究,我们知道了圆具有“一中同长”的特征。我们现在终于知道,在短时间里摆出来的图形、或是随手画出来的图形很难是一个标准的圆,因为没有做到什么?
生:没有做到“一中同长”。
师:俗话说得好“没有规矩,不成方圆”,方的东西要用矩来画,所以长方形、正方形又叫做矩形,圆的东西要用规来画,所以画圆的工具又叫做圆规。
【赏析:“学源于思,思源于疑”。课始,教师组织一个让学生“摆圆”的游戏,吊足了学生学习的胃口,给学生提供了挑战的空间。一连串思考性与挑战性极强的问题,让学生萌发了学习圆的强烈需求,很大程度上调动了学生学习的主动性与积极性,凸显了学生学习的主体地位。教师关注了学生已有的知识经验,在此基础上又让学生积累了新的经验,形成了新的技能,真正让学生用数学的思维方法去观察、分析、解决现实问题。结合正n边形到圆的演变和有关圆的史料介绍,渗透极限思想与数学文化,形成学生深厚的数学素养,推进单纯的数学教学向丰富的数学教育的转变。】
片断二:“画圆”。
师:老师找了一个简易的圆规——树杈,用它能不能在平整的沙地上画出一个圆来?如果能画出来,它有什么缺陷?
生:缺陷是画出的圆是固定的,有些粗糙。
师:拿出我们所带的圆规来,比起这个树杈,它有什么好处?
生:用圆规画圆,可大可小,而且很精准。
师:你们会用圆规画圆吗?画画看?边画边想:你是怎样做的?
师:同学们,圆的样子都是一样的,不圆的样子就各有各的不同。想想这样的“不圆”很可能是怎样被画出来的?
生:可能圆规针尖移动了,也可能圆规两脚之间的距离变了。
师:猜想很正确!谁来说说怎样做能用圆规画好圆?
生:圆心不能移动;圆规两脚间的长度固定不变;拿圆规的上部稍倾斜,转一周。
师:老师也画一个圆,你们画的圆大还是老师画的大?圆的大小由什么决定?
生:老师画的大;圆的大小是由半径决定的。
师:谁来给老师的这个圆画上一条半径?画半径关键是找哪两个点?
(学生上黑板画图并讲解半径的定义)
师:这个点可以吗?这个呢?(圆外、圆内各找一点)
生:不可以!必须是“圆上”。
师:一个圆内这样的半径有多少条?它们的长度怎样?
生:一个圆的半径有无数条,它们的长度都相等。
师:请大家在练习纸上画一个半径是4厘米的圆,并标注圆心、半径。
(学生用圆规画圆并标名称及数据)
师:这是一个足球场,看到那个大圆了吗?想一想,它是怎么画上去的?
(学生讨论并回答)
师:把圆心定在黑板上,圆就画到了黑板上;把圆心定在练习纸上,圆就画在了练习纸上;把圆心定在足球场上,圆就画在了足球场上。请大家想一想,圆心有什么作用?
生:圆心能确定圆的位置。
【赏析:比较是认识事物的基本方法。画圆的教学活动散发出浓浓的数学味,在比较中观察,在比较中启发,在比较中归纳。通过树杈画圆与圆规画圆的比较,体会圆规画圆的优越性;通过圆的作品与不圆作品的比较,归纳圆正确的画法;通过教师画的圆与学生画的圆的大小比较,揭示半径的作用;通过点在圆外与圆内的比较,强化半径的定义;通过黑板上的圆、练习纸上的圆和足球场上的圆的比较,感悟圆心的用途。五次“比较”,目的明确,循序渐进,为建构圆的概念创造了有利的条件。】
片断三:“折圆”。
师:老师这里有一张圆形纸片,想知道它的半径是多少,你有办法吗?
生:必须找出圆心,才可以准确地测量出半径的长度。
师:怎样找出这张圆形纸片的圆心呢?
(请一位学生上台演示,两次对折找到了圆心)
师:老师把这条折痕画出来,这条线在圆里叫什么?这条线有什么特点?
生:这条线在圆里叫直径,通过圆心并且两个端点在圆上。
师:一个圆中有多少条这样的直径?这些直径的长度怎样?
生:在一个圆中有无数条直径,长度都相等。
师:沿着直径所在的这条直线对折,我们可以把这个圆的两部分完全重合在一起,说明圆是怎样的一种图形?
生:圆是轴对称图形,直径是圆的对称轴,圆有无数条对称轴。
师:因为直径是一条线段,对称轴是一条直线,所以应该说直径所在的直线更贴切。
【赏析:教师并没有按部就班地教学圆的对称性,而是把它与直径的定义结合起来教学,即整体着眼,局部处理,自然巧妙,别具匠心。通过测量圆的半径来诱发学生展开找圆心的活动,学生两次对折圆形纸片找到了圆心,描画折痕引入了直径的定义,观察直径两侧的大小来揭示圆对称性的特征。这一系列的活动,层层递进,水到渠成,真正让学生经历和体验了数学学习的过程。可以说学生“折圆”折出了新的认知,是“摆圆”“画圆”的延伸,数学活动贯穿始终,浑然一体,促进了学生对圆概念的顺利内化。】
