基于改进FAHP的无车承运人合作伙伴选择研究

□ 史丹青

(华信咨询设计研究院有限公司，浙江 杭州 310052)

1 前言

从2016年8月交通运输部办公厅印发《关于推进改革试点加快无车承运物流创新发展的意见》，到2016年10月至2017年12月期间，在全国开展道路货运无车承运人试点工作，再到2020年国家决定将重点发展50家无车承运人品牌企业，无车承运人在短短几年内取得了快速的发展，但目前也面临着诸多问题，主要表现在合作企业之间缺乏统筹协同，整体运营效率不高；各企业主体之间信息缺乏共享机制，信息化支撑水平不高；合作企业服务水平参差不齐，整体服务能力有待提高；企业间合作稳定性不高等。随着无车承运人行业进入调整期，多数无车承运人将面临被行业淘汰，究其原因主要是多数无车承运人企业在成立初期没有正确选择合适的合作伙伴。本文将基于此，研究无车承运人如何科学选择合作伙伴，为现有的无车承运人优化合作伙伴选择模型和即将成为无车承运人企业建立合作伙伴选择机制提供理论参考。

无车承运人是指不拥有车辆而从事货物运输的个人或单位，其主要从事运输组织、货物分拨、运输方式和运输线路的选择等工作，而将运输活动交给实际的承运人，即无车承运人合作伙伴[1]。无车承运人合作伙伴一般是具有实际运输能力的物流企业，通过与无车承运人的合作来提高运输业务量，增加企业收入。同时，对于无车承运人来说，合作伙伴的选择将直接影响到承运质量和经济利益。

目前针对合作伙伴选择的相关研究较多，理论成果较为丰富。李蕊[2]基于熵构建了以RBF神经网络对供应链合作伙伴的选择进行了研究。刘伯超[3]等使用层次分析法(AHP)构建高端装备制造企业物流外包合作伙伴选择模型，为高端装备制造企业物流外包合作伙伴选择提供理论依据与实践路径。Petroni[4]等提出应用多目标逼近法PCA(Principle Component Analysis)，为采购经理提供采购合作伙伴选择决策模型。Chan[5]等将层次分析法与遗传算法相结合来解决供应链管理中的合作伙伴选择问题。苏菊宁[6]等基于制造商与物流供应商长期合作的伙伴关系，从成本、服务质量、合作稳定性以及综合实力四个方面设计了物流合作伙伴评价指标体系，建立了灰色评价与层次分析法相结合的多层次灰色评价模型，并进行了算例验证。目前，无车承运人的合作伙伴选择研究相对较多，学者的研究集中于供应链合作伙伴的选择。考虑到无车承运人发展面临的问题，本文综合使用熵权法、层次分析法和模糊综合评价法构建无车承运人合作伙伴选择模型。

2 无车承运人合作伙伴选择评价指标体系构架

本质上，合作伙伴就是无车承运人的运力供应商，只是二者的关系不仅仅是满足于“供与求”，而是要建立基于“共赢”的长期合作伙伴关系。在合作伙伴选择时，无车承运人与大部分企业均未合作过，这种情况下，只能通过企业已经取得业绩来了解情况，比如通过调研了解其信誉情况等。由于无车承运人自身没有车辆，因而合作伙伴的配套设施也成为无车承运人比较关注的地方，比如运输车辆、仓储条件等。对于无车承运人，合作伙伴能否与其在组织、业务、信息等方面实现快速协同、合作，将直接影响着物流运输效率，甚至是运营成本。此外，合作伙伴的企业长远发展能力，对于与之建立“共赢”的长期合作伙伴关系也有较大的影响。

基于以上分析，并结合前人的研究成果[7-9]，构建出符合无车承运人合作伙伴选择指标评价体系，如表1所示：

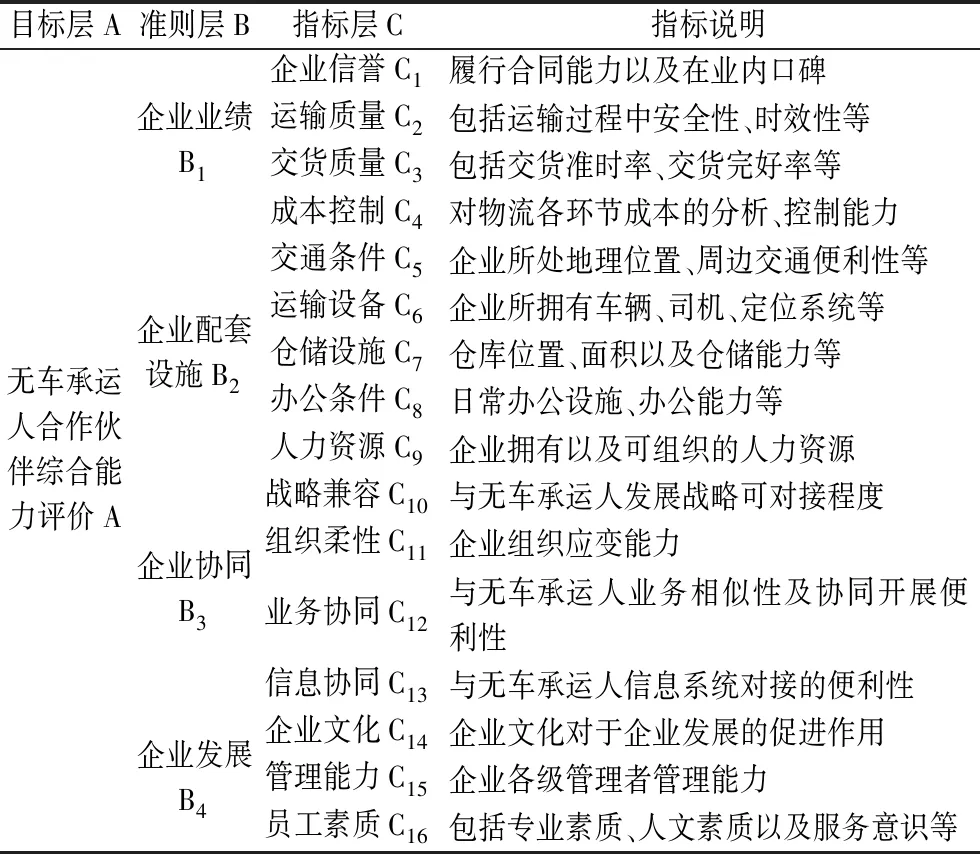
表1 无车承运人合作伙伴选择指标评价体系

3 无车承运人合作伙伴选择模型构建

3.1 基于熵权法和层次分析法的评价指标权重确定

经过多年的研究与应用实践表明，由于不同的专家打分而造成层次分析法分析结果具有较大的主观性。为了确定更加客观的评价指标权重，本文将采用熵权法对层次分析法结果进行修正。

3.1.1 改进的层次分析法

原有的层次分析法要进行一致性检验，不满足一致性的判断矩阵要进行修正再检验，直到满足一致性，过程比较繁琐。本文对层次分析法进行改进，不必进行一致性检验，简化计算过程，提高评价效率。

改进的层次分析法[10]基本思想：若A没有B重要，用0表示；若A与B同等重要，用1表示，若A比B重要，用2表示，以此判断标准对准则层和指标层进行两两重要性评判，建立初始判断矩阵。具体步骤如下：

②构建判断矩阵A=(aij)n×n，其中aij满足：

(1)

③计算判断矩阵A各指标近似权重。

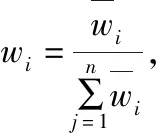
(2)

3.1.2 熵权法

熵权法[11]是信息论中一种比较客观的指标权重赋值方法。信息论认为信息是系统有序程度的一个度量，熵是系统无序程度的一个度量；如果指标的信息熵越小，该指标提供的信息量越大，在综合评价中所起作用理当越大，权重就应该越高。熵权法确定指标权重的具体步骤如下：

①对判断矩阵A归一化处理，得到标准矩阵M。

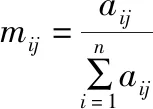
(3)

②计算信息熵ej。

(4)

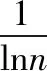
③计算指标的信息熵权重γi。

(5)

④用信息熵权重ri修正层次分析法得到的近似指标权重，得到最终指标权重ωj。

(6)

3.2 基于模糊综合评价法的合作伙伴综合能力评价模型构建

模糊综合评价法是人们对评价对象的不同影响因素做出相应的非精确性评价，即模糊评价，并借助模糊数学理论进行量化处理，并最终得到精确结果的一种将模糊不确定性问题量化处理的分析方法。以下应用模糊综合评价法构建无车承运人合作伙伴综合能力评价模型。

3.2.1 建立合作伙伴选择评价因素集

评价因素集：U={u1,u2,…，ui…un}，表明指标层中共有n个主要的因素需要评价，每个一级指标u包括的k个二级指标记作uk。根据已构建的指标体系中可知共有4个指标，所以U=(u1,u2,u3,u4)，即：

U={企业业绩，企业配套设施，企业协同，企业发展}

u1={企业信誉，运输质量，交货质量，成本控制}

u2={交通条件，运输设备，仓储设施，办公条件，人力资源}

u3={战略兼容，组织柔性，业务协同，信息协同}

u4={企业文化，管理能力，员工素质}

3.2.2 构建决策评语集

决策评语集：对有可能出现n个评语，构成评语集V=(v1,v2,…，vn)。不同的决策问题，评语集的构建也不尽相同。本文对无车承运人合作伙伴选择进行决策的依据就是其在综合能力评价下的“好坏程度”，可令评语集为V={优，良，中，差}。

3.2.3 建立评价隶属矩阵R

对各指标确定评判等级标准，并根据这个标准确定U对于评语集V的隶属向量R为Rij=(rij1，rij2,rij3,rij4)，其中rijh=Vijh/n(h=1,2,3,4)，n为参与评价的专家数量，则评判隶属矩阵R为：

(7)

3.2.4 综合评价

根据层次总排序Y和隶属度矩阵R，可计算出模糊综合评价集B，进而得到相应的结论，此处采用加权运算。

①确定模糊综合评价集B。

(8)

②确定U对于V的权重。

B=Y∧R作归一化处理后记为Bt，Bt为U对于V的隶属度向量，即为总的评价结果：

(9)

3.2.5 结果处理

至此，则可以对评价结果进行处理，首先将评判集V中各指标进行量化，再利用公式求出各方案P的总体得分情况，即：

(10)

4 实证分析

以某无车承运企业为例，假设有10家候选合作伙伴，分别为H1、H2……H10，应用本文构建的模型进行合作伙伴选择。

4.1 应用改进的层次分析法确定指标初始权重

邀请8位专家组成专家小组，由专家组对指标体系的相对重要性进行评估。根据专家组最终评估结果，构建B层对A层的初始判断矩阵，如表2所示：

表2 B层对A层的初始判断矩阵

然后，构建判断矩阵A=(aij)n×n，并计算初始权重，得到表3：

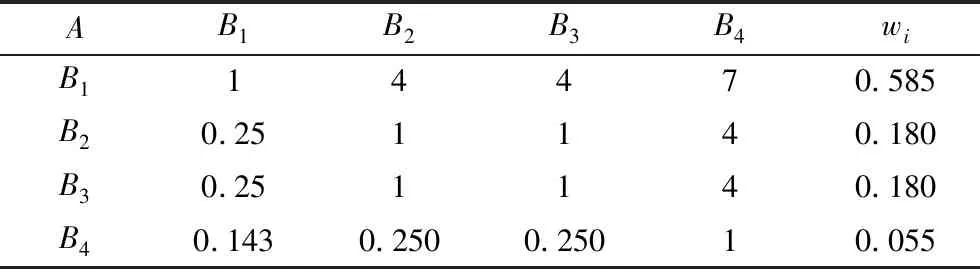
表3 B层对A层的判断矩阵及权重

同理，可计算出C层对B的权重，由此得到评价体系中全部评价指标初始权重，如表4所示：

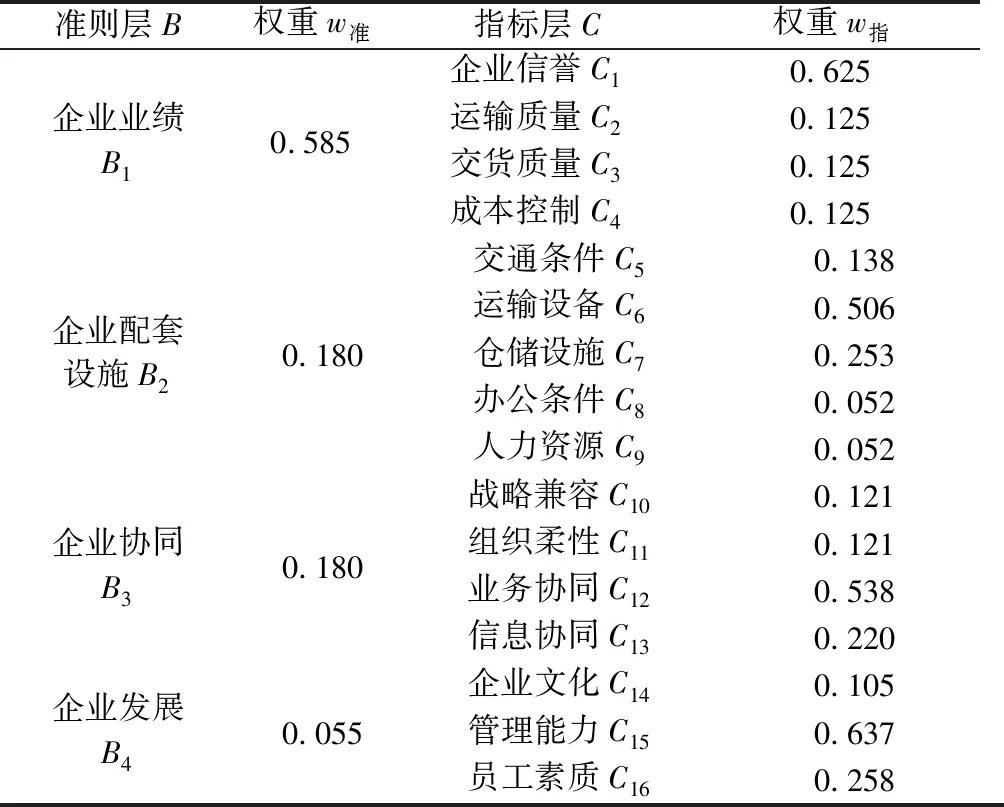
表4 基于层次分析法确定的评价指标初始权重

4.2 应用熵权法修正指标权重

首先，将矩阵A归一化，得到：

然后，应用MATLAB软件求解信息熵权重，得到：

同理，可计算出C层对B的信息熵权重。最后，应用公式(6)得到修正后的评价体系指标权重，如表5所示：

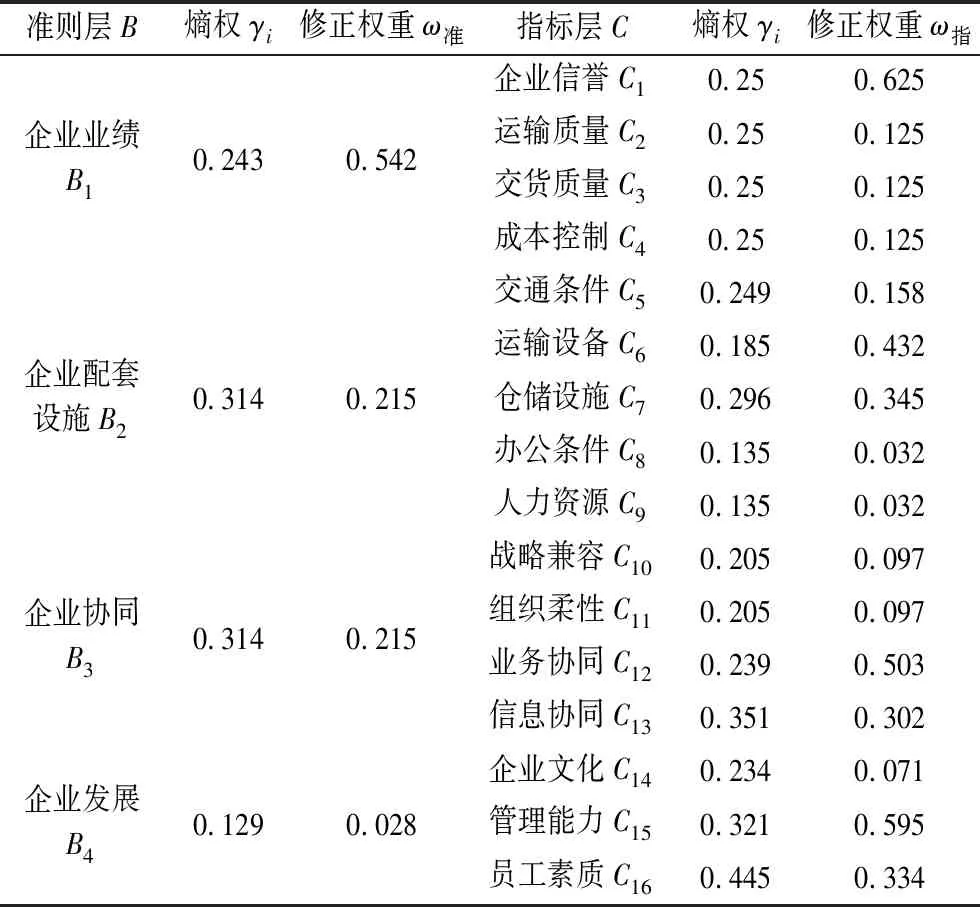
表5 基于层次分析法确定的评价指标初始权重

进而得到各指标综合总权重：

ω总=(0.339,0.068,0.068,0.068,0.034,0.093,0.074,0.007,0.007,0.021,0.021,0.108,0.065,0.002,0.017,0.009)

4.3 应用模糊综合评价法评选合作伙伴

4.3.1 建立评价隶属矩阵R

对专家进行访谈，邀请专家依据选址评价指标体系对10家候选企业分别进行打分，并建立评价隶属矩阵R。由于篇幅有限，以下以候选企业H1、H2为例进行计算。

4.3.2 模糊综合评价

根据公式(8)B=Y∧R=ω总∧R，归一化后得：

同理：

4.3.3 结果处理

规定评判集V中各元素的量化值[12]为V1=100，V2=80，V3=60，V4=40，根据公式(10)计算得到各候选企业的评分排名如下表6所示：

表6 候选企业最终得分及排名

根据评分排名即可依次选择一家或多家合伙伙伴。

5 结束语

无车承运人虽然已经在国外得到很好的发展，但是在我国物流市场中还是一个新兴事物，无车承运人合作伙伴的选择正是发展阶段最为关键的工作。本文结合国内外相关理论研究，设计了一套符合我国物流市场环境的无车承运人合作伙伴评价指标体系，应用改进的层次分析法、模糊综合评价法构建合作伙伴选择模型，在此过程中，为了使评价过程更具客观性，应用熵权法对层次分析法得到的结果进行修正。通过实证分析表明，本文构建的指标体系及模型具有良好的实用性。