基于回归模型和因子分析的区域经济活力研究
2020-11-04姚朝乾
□ 姚朝乾,张 骏
(南京林业大学 汽车与交通工程学院,江苏 南京 210037)
近年来,受到中美贸易战的影响,国内有一部分企业受其影响,出现了区域经济效益大幅度下滑趋势,甚至2018年出现了企业倒闭潮的现象,严重影响了区域经济活力,因此,在经济萧条情况下,研究区域经济活力有一定的现实意义。
1 研究概况
王成勇,聂华林通过产业集聚对区域经济活力进行了研究;石斌,刘思峰对南京市的区域经济活力开展了研究;张婷婷,汤茂林通过时空演化对长三角区域经济韧性进行研究;何汝群,王卫则通过因子分析对珠江-西江经济带城市经济活力进行研究;潘桔,杨丹通过分位数回归的方法研究了中国区域经济的差异。
2 经济活力
2.1 经济活力的定义
经济活力是指一个国家在一定时期内经济中总供给和总需求的增长速度及其潜力。从投资角度,主要涉及国民生产总值的增长率(经济增长率)、固定投资率(资本积累率)和储蓄率及其变化等。本文将区域经济活力简化为GDP(国内生产总值)。
2.2 经济活力的影响因素
各国学者提出了许多很有价值的区域发展理论与模式,如要素禀赋理论、输出基础理论、增长极理论、产业集聚理论、三螺旋理论、累积因果理论、核心——外围模式理论等,而本文根据这些理论将影响区域经济活力的主要因素分为宏观和微观的影响因素,本文选取宏观的影响因素:人口数量、企业数量、企业资产总计、从业人员数量、全社会固定资产投资、出口总额、利润总额。
3 构造影响南京经济活力的关系模型
3.1 回归模型
回归模型是对统计关系进行定量描述的一种数学模型,只含有一个回归变量的回归模型称为一元回归模型。
3.2 指标体系的构建
区域经济活力主要指标有:人口数量、企业数量、企业资产总计、从业人员数量、全社会固定资产投资、出口总额、利润总额。
3.3 原始数据的标准化处理
在区域经济活力的评价中,为了消除指标量纲的影响以及变异范围影响,需要对数据进行标准化处理,使其具有可比性,一般用下式进行:
3.4 建立评价函数
一元回归函数:
y=β0+βixi+εi
其中,β0…βi是i+1个待估计的参数,εi是相互独立且服从同一正态分布N(0,σ2)的随机变量,y是随机变量;x可以是随机变量,也可以是非随机变量,βi称为回归系数,表征自变量对因变量影响的程度。
3.5 南京市情况分析
根据影响因素构建南京经济活力多元单目标回归模型,原始数据如下表1所示。
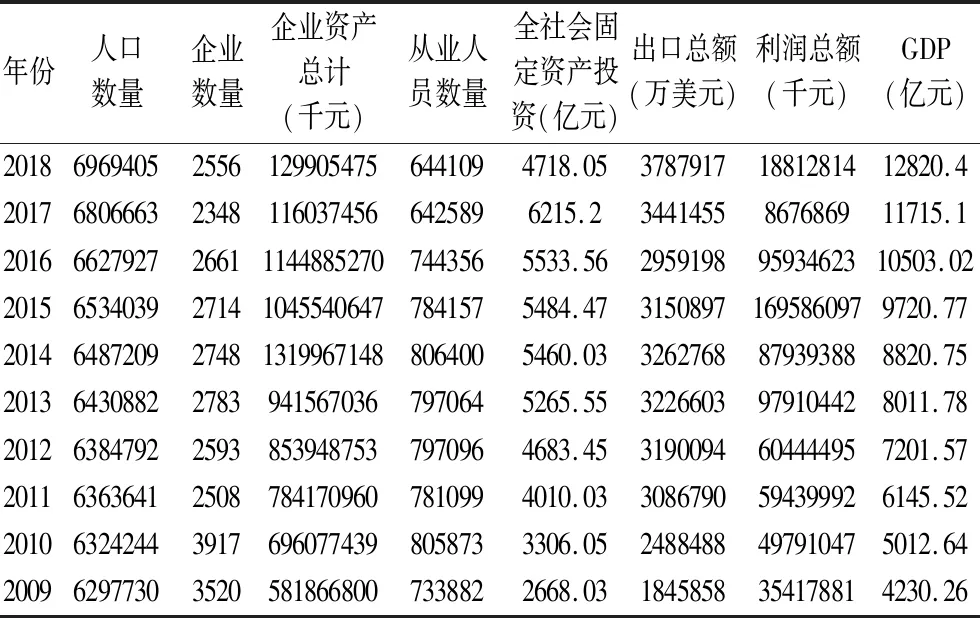
表1 原始数据
人口总数与GDP的拟合回归如下图1所示。
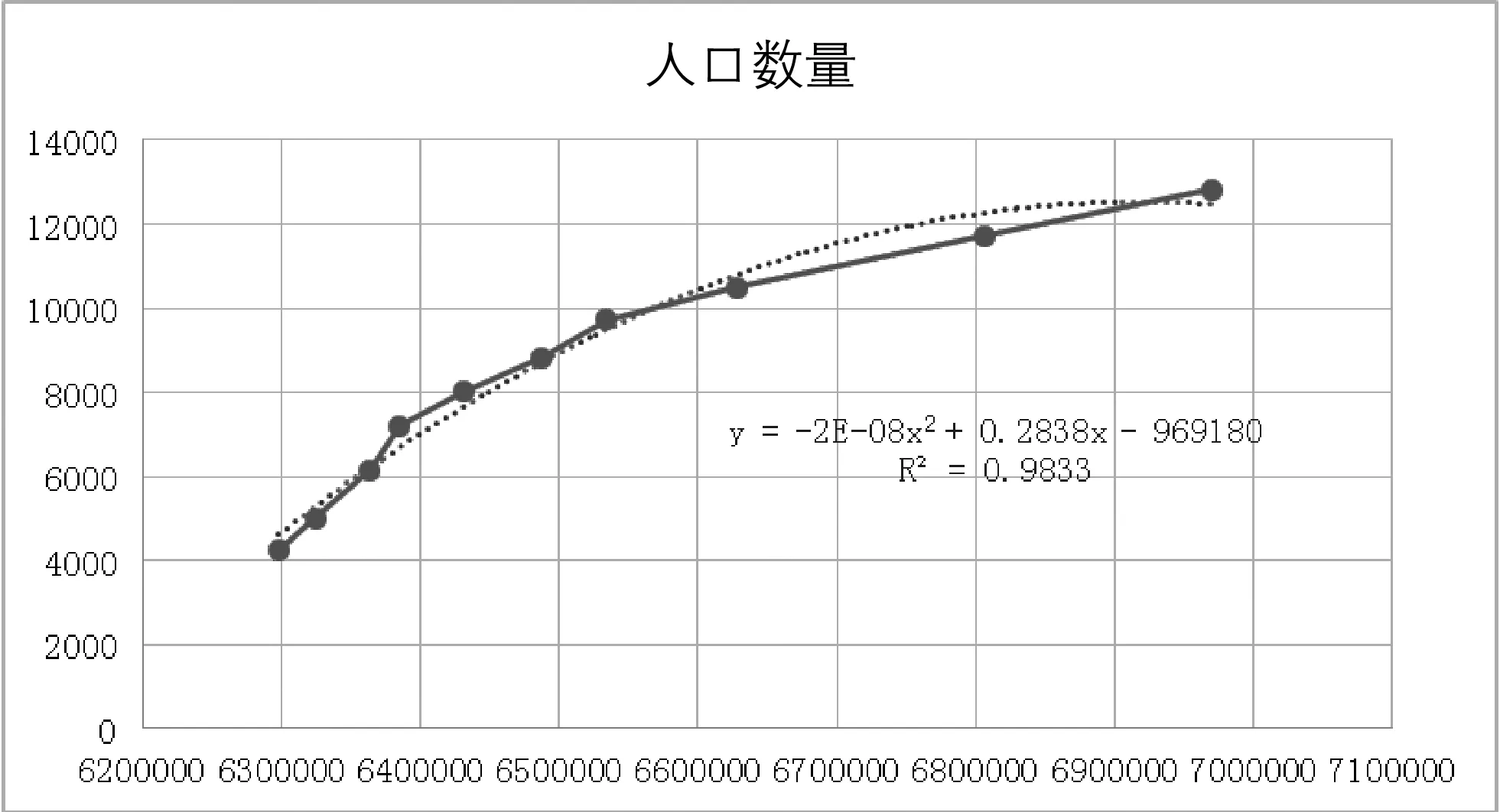
图1 人口总数与GDP的拟合回归图
企业数量与GDP的拟合回归如下图2所示。
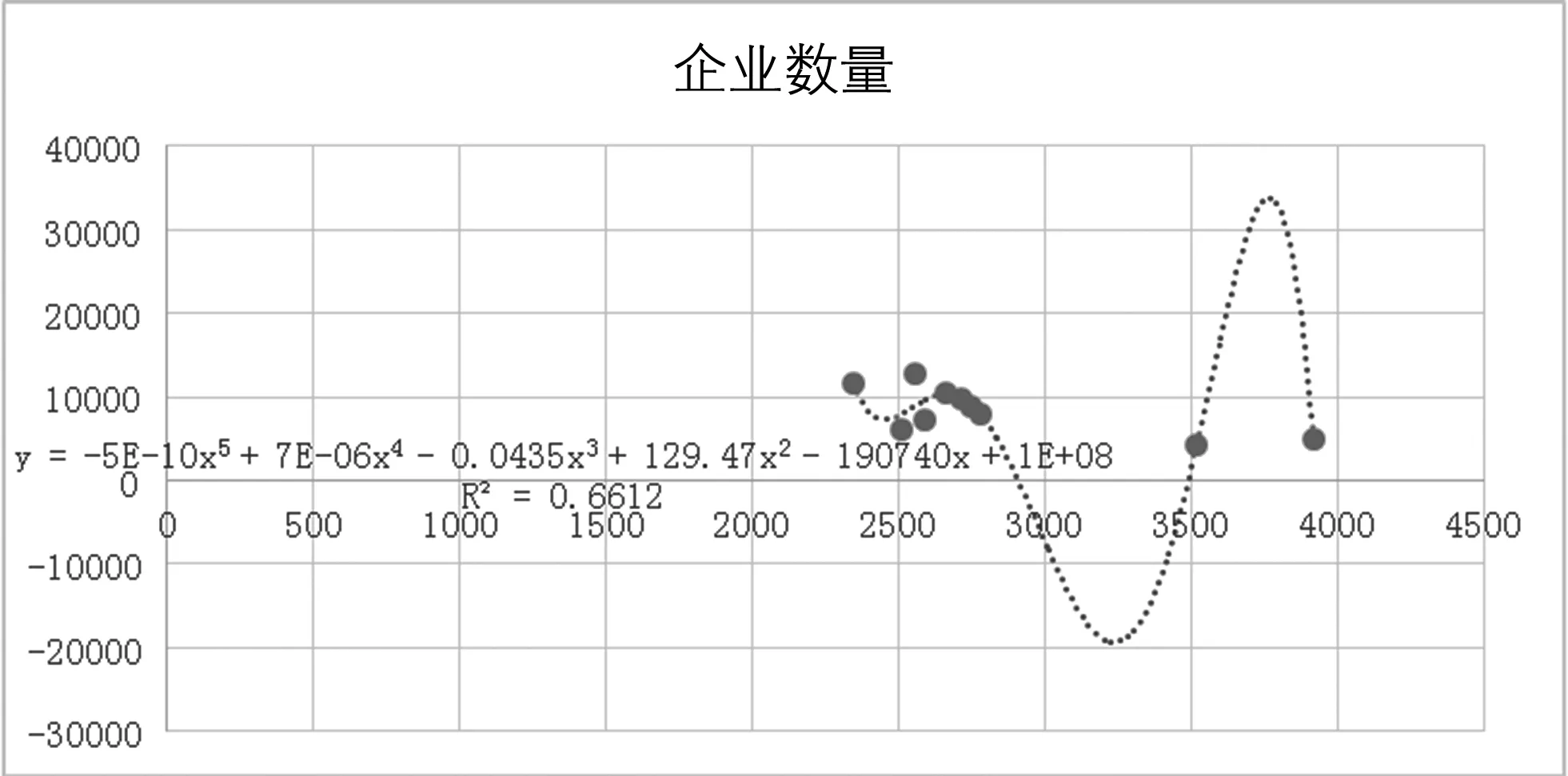
图2 企业数量与GDP的拟合回归图
企业资产与GDP的拟合回归如下图3所示。
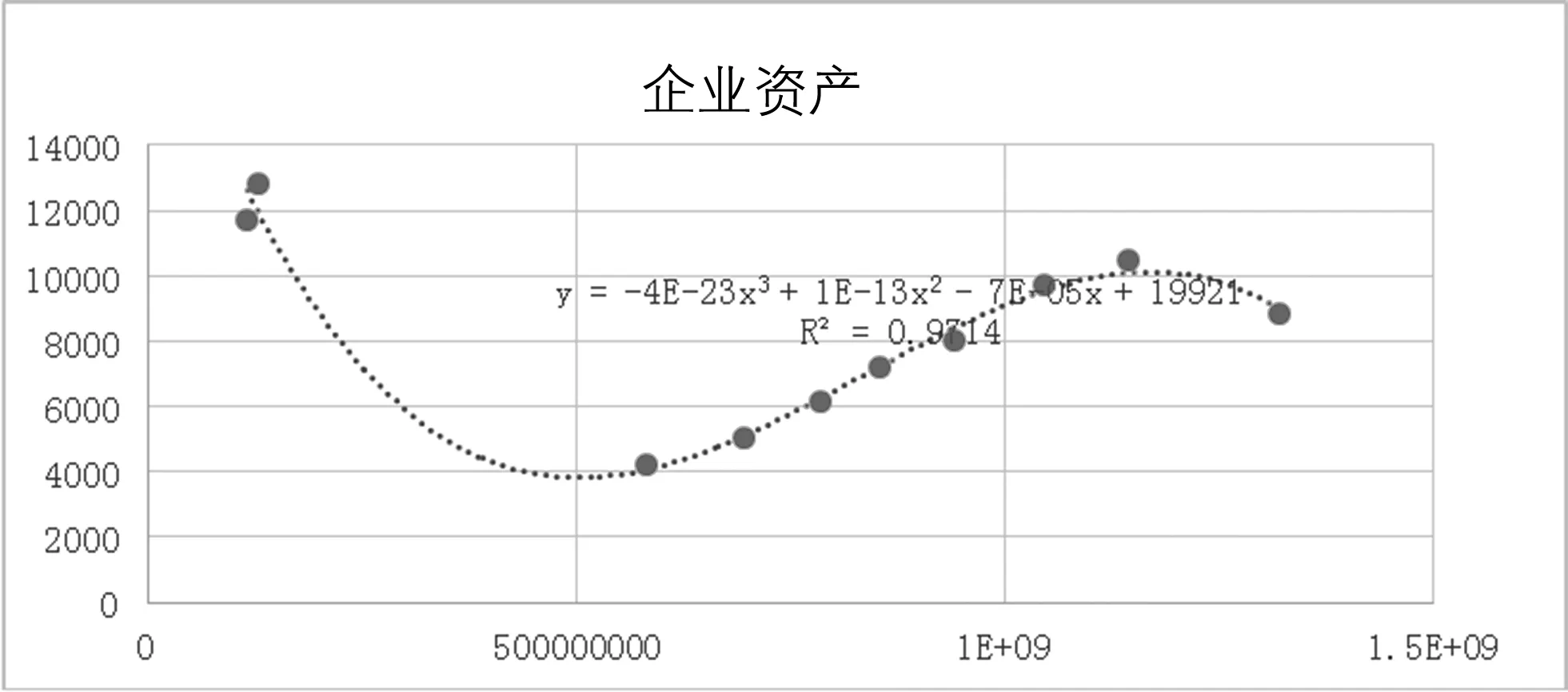
图3 企业资产与GDP的拟合回归图
从业人员数量与GDP的拟合回归如下图4所示。
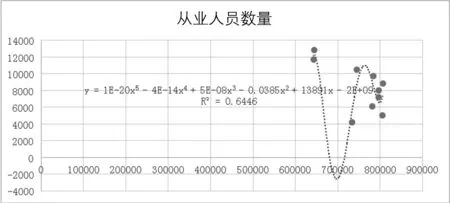
图4 从业人员数量与GDP的拟合回归图
全社会固定资产投资与GDP的拟合回归如下图5所示。
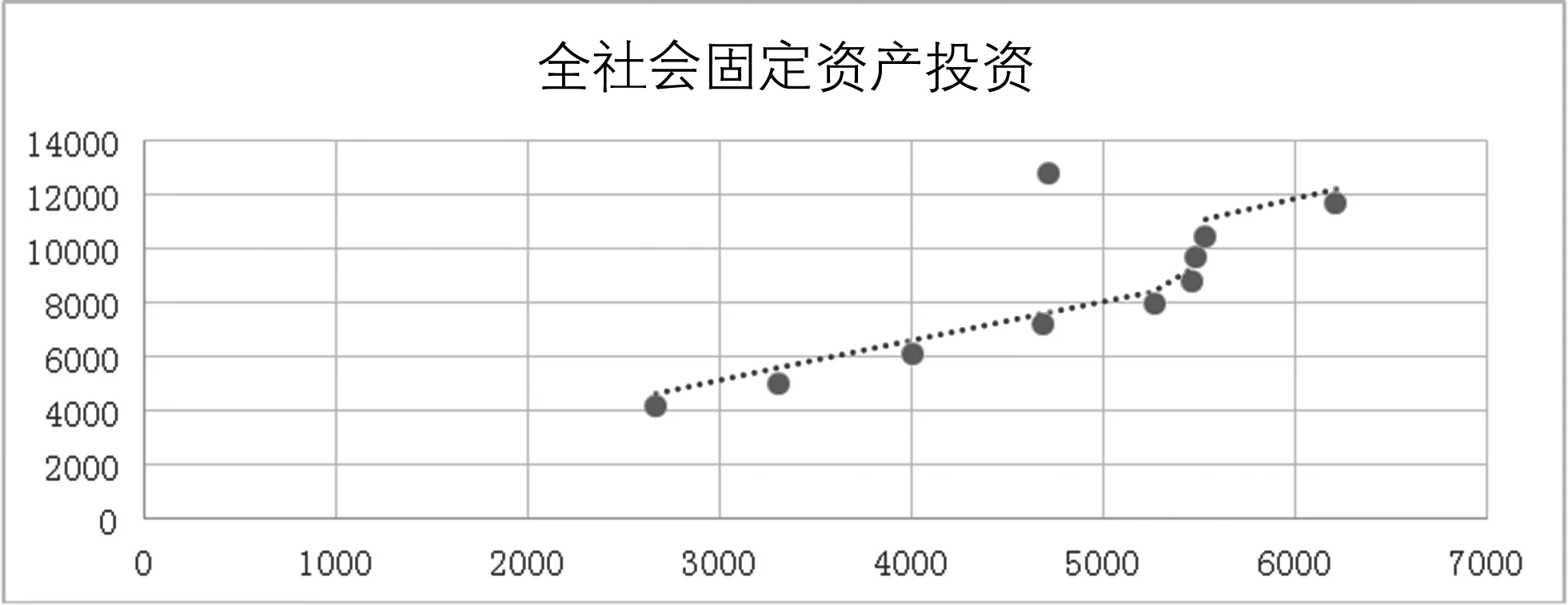
图5 全社会固定资产投资与GDP的拟合回归图
出口总额与GDP的拟合回归如下图6所示。
利润总额与GDP的拟合回归如下图7所示。
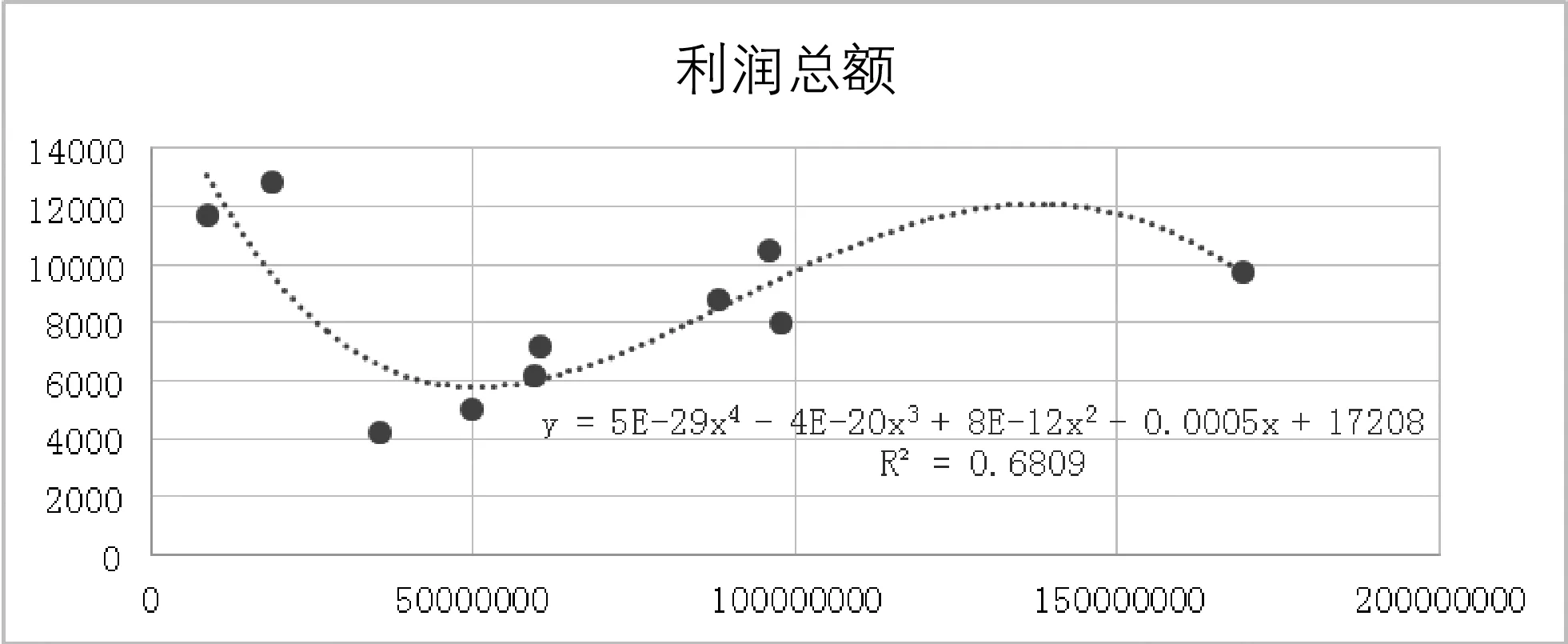
图7 利润总额与GDP的拟合回归图

表2 各城市GDP原始数据
通过对比分析7个回归方程的系数,可以得出,经济活力影响因素的重要度排序如下:
人口数量>出口总额>企业资产>全社会固定资产投资>企业数量>从业人员数量>利润总额
结论:影响经济活力的最重要因素是人口数量,影响最小的是利润总额。根据趋势图看出,人口数量越多,企业活力越好,越有利于区域经济发展。
4 因子分析理论
因子分析是利用降维思想,从研究原始变量相关矩阵出发,把一些具有错综复杂关系的变量归结为少数几个综合因子的一种多变量的统计分析方法。研究变量之间的相关关系,称之为R型因子分析;研究样品之间的相关关系,称之为Q型因子分析。
4.1 因子分析
其中,y1,y2,…yp为实测变量,aij为因子载荷,fi(i=1,2,…,m)为不可测变量即公共因子,gi(i=1,2,…,p)为特殊因子。
4.2 检验原始变量
常用的检验原始变量是否适合作因子分析的方式有四种:变量间相关系数矩阵、巴特利特球体检验、反映像相关系数检验、KMO检验。对于变量间相关系数矩阵,如果大部分相关系数都大于0.3时,认为变量间存在较强的相关性,适合作因子分析;对于巴特利特球体检验,当P值小于给定显著性水平时,拒绝原假设,认为原始变量之间存在相关性,数据就适合作因子分析,若未通过检验,数据就不适合作因子分析。
4.3 判断提取的公共因子数
公因子提取方法主要有:最大似然法、主成分分析法、主轴因子法、加权最小二乘法、广义最小二乘法、α因子提取法等,常用最大似然法和主轴因子法。常用特征根大小、因子的累计方差贡献率、碎石检验和平行分析这四种方法确定公因子个数。为了便于公因子的重新命名,通常需要对因子进行正交旋转或斜交旋转。正交旋转和斜交旋转的方法有很多,而常用的正交旋转法为方差最大法,常用的斜交旋转法为Promax旋转。如果斜交旋转公共因子之间相关系数较大则可以采用斜交旋转,较小时选择正交。
4.4 计算因子得分并进行结果阐释
选取直辖市以及省会城市的10年GDP数据,计算出每个样本在不同因子上的具体得分,对得分进行分析。
4.4 分析结果
上海>北京>深圳>广州>天津>重庆>武汉>成都>苏州>杭州>南京>长沙>青岛>郑州>西安>沈阳>昆明。在过去十年,北上广一线城市的区域经济活力较好,根据趋势上可看出,总体都呈上升趋势,因此,企业变化会对当地的经济活力造成一定的影响。
5 提高区域经济活力方案
建立合适的市场竞争机制,企业要不断提高自身的核心竞争力以及不断进行自身的转型升级;政府可通过相关政策引进外来大型企业,吸引小型企业来本区域发展,人才引进以及相关鼓励政策。
