考虑声场空间相关的结构声振响应预示方法
2020-11-04高珂佳秦朝红
韩 丽,高珂佳,秦朝红
(1.北京强度环境研究所 可靠性与环境工程技术重点实验室;2.北京强度环境研究所:北京100076)
0 引言
航天飞行器在发射和飞行阶段所经受的发动机喷流噪声、上升主动段跨声速和承受最大动压飞行时产生的气动噪声,以及再入大气层超高速飞行时产生的气动噪声等激励大都是宽频带随机振源,其频率范围为10~10 000 Hz,声压级有的超过160 dB,它们引起飞行器结构的均方根加速度响应可达几十个g,并使有效载荷或仪器设备承受高量级振动和高声压级噪声的恶劣动力学环境,这类振动通常统称为“声振”[1]。声振对航天飞行器系统产品的主要影响是引起结构与仪器设备元件的共振、机械应力疲劳等,轻则使仪器设备不能正常工作,严重时甚至能导致整个飞行任务的失败。因此,需要对航天飞行器进行大量的地面动力学环境试验以确保其高可靠性[2]。地面环境试验中动力学环境条件的制定,可以依据既往飞行试验的遥测数据,但是大量的实测数据只有在飞行器生产研制出来并经过多次飞行试验之后才能得到,这势必会使环境条件的制定滞后于飞行器设计,而且代价昂贵。因此,在飞行器设计阶段,进行动力学环境预示是极为重要的[3]。
目前用于声振响应预示的方法包括有限元法、统计能量法、边界元法及能量有限元法。统计能量法是用统计的观点,从能量的角度来分析复杂结构在外载荷作用下的响应,在某种程度上忽略了结构的具体细节,因此经常不能得到局部结构响应,无法与试验对比[4]。边界元法对于复杂结构存在计算量大、内存占用量大等缺点。能量有限元法是一种新兴的方法,具有一定的优势,但能量有限元理论体系还需要进一步完善,目前的应用还只局限于几类简单问题,尚无法用于工程问题[5]。有限元法可以获得局部结构响应,可以较精确地描述振动场分布,是动力学分析有力的工具;但对于大型复杂结构,由于节点与单元众多,载荷施加中完整考虑声场的空间相关特性很困难,目前通常将噪声场按完全相关或完全不相关处理[6-7],导致声振响应预示结果与实际差别较大[8-9]。
为了解决利用有限元法进行声振响应预示时存在的上述问题,文献[9]进行了初步尝试,采用分区的思想,对互谱矩阵做了简化,减少了互谱的数量,使得在Nastran 中可以手动施加,取得一定效果。本文更进一步,研究在有限元中完整考虑空间相关的声场载荷施加方法,并以主流动力学分析有限元软件MSC.Nastran 为基础进行算法研究及二次开发,编制软件来预示航天飞行器噪声试验声振响应,并与试验结果进行对比,以验证该方法的有效性,解决传统中高频响应预示方法不能给出局部结构振动响应的问题,旨在为航天飞行器力学环境预示提供一种新途径。
1 声振响应分析
在声场激励有关变量如入射角度等不清楚的情况下,混响声场是很适用的模型,代表了各种可能声场激励的平均效果[10]。以下分析描述混响声场的充分必要参数。

其中,r(ω,ζ)即为声场的空间相关系数,r(ω,ζ)=exp[-jΦ(ω,ζ)]。
由式(5)可知,对于时间、空间坐标都平稳的噪声场而言,表征该噪声场的充分必要参数即为声压的自功率谱和空间相关系数。
结构的线性运动微分方程为

式中:M、C和K分别是结构系统的质量矩阵、阻尼矩阵和刚度矩阵;x(t)是结构系统的位移;P(ω)是作用在结构系统上的载荷。

式中:d为结构表面j、k两点之间的距离;K是波数,K=ω/c,c为声速。
2 基于有限元法的声场载荷建模实现
由式(10)可看到进行声振响应分析需确定频响函数Hij(ω)及载荷谱Wjk(ω)。由于声场具有空间相关性,因此在有限元中不仅要给定声压的自谱,还要给定任两点之间的压力互谱。式中的下标j和k在有限元中分别为单元j和单元k,在Nastran 中要给定某两个单元之间的压力互谱,需要在计算频响阶段,就将作用在这两个单元上的力作为两个工况(loadcase),换言之,一个结构有n个单元就需要有n个工况,才能在随机响应分析中给出n个单元之间的互谱。
综上,大型复杂结构的单元数量十分庞大,要完整描述声场载荷的空间相关性,工况及互谱数量也会十分庞大;此外,结构声振响应预示一般在频域开展,频率离散后互谱数量会进一步增多,在Nastran 中实现完整的声场载荷施加具有很大的困难。因此利用有限元方法计算声载荷引起的结构振动响应时,主要难点在于描述压力场的谱密度如何建模和施加。为解决该问题,本文提出完整考虑空间相关的声场载荷施加二次开发算法如下:
1)依次设定loadcase 1、loadcase 2、 ···、loadcasen,在1号、2号、 ···、n号单元上施加单位力,每个单元上的单位力是一个工况,bdf 文件中包含这n个工况,然后进行频率响应计算,生成频响计算结果文件。
2)设压力场的自谱为Wp。选定1号单元为参考单元,利用式(12)及式(5)计算其与2号、3号、···、n号单元之间的互谱W12、W13、 ···、W1n;依次计算2号与3号、4号、 ···、n号单元之间的互谱W23、W24、 ···、W2n,这里的谱矩阵是对称的,因此不需要另外计算2号与1号、3号与2号、4号与3号 ···单元之间的互谱。
3)从1)中生成的频响计算结果文件中提取各节点的频率响应,形成频响函数矩阵,结合2)中给出的功率谱矩阵,按式(11)计算感兴趣节点的随机振动响应。
4)从计算的随机响应结果文件中提取给定节点的响应,以曲线的形式表示,并与相应的试验结果对比。
3 考虑声场空间相关的结构声振响应预示软件
基于上述算法编制相应的软件系统,实现声场载荷的有限元建模及响应预示。该系统包括与Nastran 的接口开发、载荷施加与响应预示、模型与曲线显示等。
1)导入接口实现
系统具有bdf 格式文件接口,能够输入输出用于Nastran 频响分析求解的bdf 格式文件。Nastran的输入文件*.bdf 中包含有限元模型的完全描述,包括执行的分析类型、模型信息、载荷信息等;系统通过在接口程序中建立关键字列表,能够支持bdf 文件各部分的读入写出功能。
系统能够读入Nastran 求解结果生成的op2文件。op2文件中包含有限元模型及仿真结果的完全描述,包括计算结果的输出要求、单元与材料的物理参数、载荷工况、速度、加速度、应力、应变等仿真计算结果。数据以数据段的形式存储于op2文件中。系统能够支持以上各部分的读入功能。
2)载荷施加与响应预示
有限元模型包括表面壳体结构及内部仪器设备等,而声场载荷仅加载于声场与结构的交界面上,因此需提取有限元模型表面信息,才能实现载荷的自动施加。通过渲染机制生成的三维模型表面信息功能,可以用于声振载荷所施加结构的表面信息提取。在此机制下进行模型信息选取时,所选取的均为模型表面内容,包括表面节点、表面单元等,从而使表面声场载荷能够方便地施加。
利用前述算法编程实现bdf 文件的修改、求解并生成频响函数矩阵;根据给定的自谱,利用式(5)、式(12)计算得到声场载荷功率谱并生成矩阵。对三维表面信息处理后,提取所要施加载荷的表面单元,将声场载荷施加于结构表面;然后按式(10)计算得到测点的声振响应。
3)模型与曲线显示
模型显示部分包括了模型显示功能与结果显示功能,并实现显示效率的提升。以本部分为核心,其他接口模块、数据库系统和用户界面作为辅助功能模块,共同实现三维模型展示的全部功能。模型显示模块对显示窗口的操作进行管理和控制。基本显示功能包括模型的旋转、平移和缩放,单元节点的拾取,以及云图的显示等。
曲线显示模块可以实现声振响应仿真结果与试验结果曲线对比分析功能。模块具备曲线静态显示/隐藏功能,曲线显示在单独的曲线窗口中,具备多窗口功能,同一窗口可显示多条曲线,曲线的线型、颜色和标记点可以自定义,曲线坐标系可以线性/对数形式自定义选择,且有自动缺省配置。
4 预示与试验结果的对比
对某试验件开展噪声试验。该试验件为某导弹仪器舱,舱段为复合材料,仪器支架为井字梁结构,其上的主要仪器为真实产品,部分仪器采用配重模拟。试验中布置噪声测点,用传声器实时测得的噪声声压级(总声压级143 dB)如图1所示。
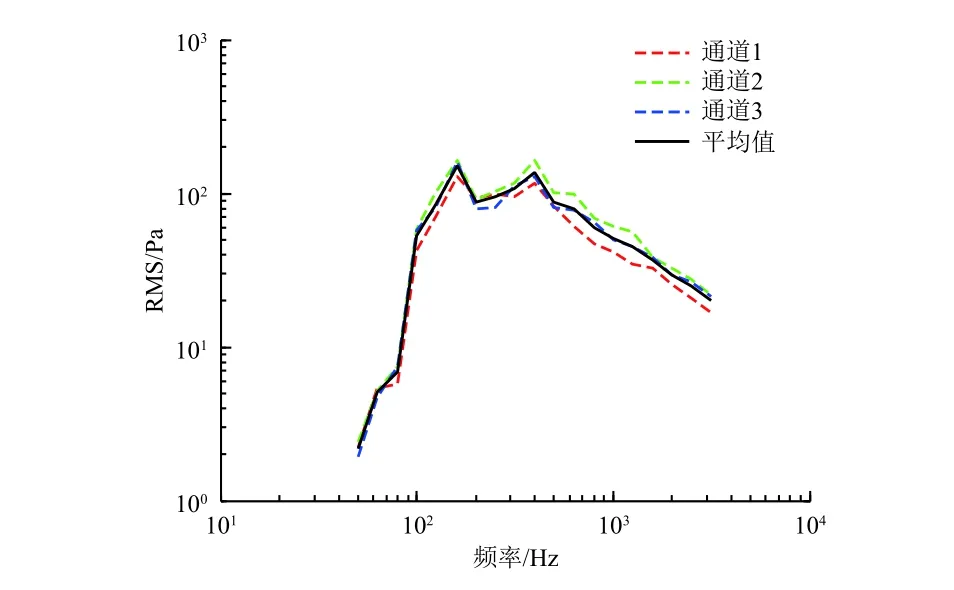
图1 混响场噪声载荷谱Fig.1 Reverberant acoustic experiment control spectrum
试验中在试验件上布置8个振动测点,实测的振动响应如图2所示。
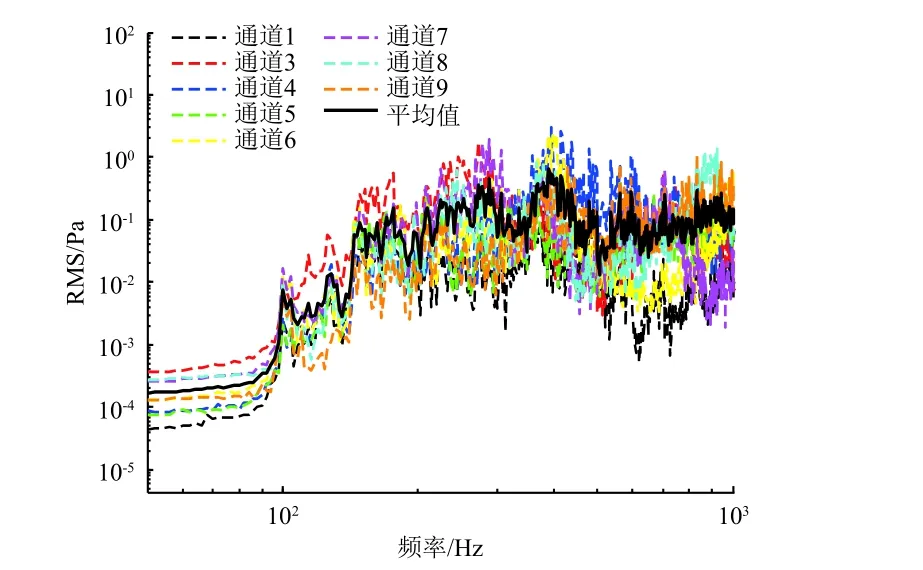
图2 振动测点响应Fig.2 Experiment acceleration responsesof the test piece
建立试验件三维有限元模型,舱段采用壳单元模拟,仪器支架采用梁单元模拟,主要仪器采用实体单元模拟,其他仪器采用质量单元模拟,整体质量特性及连接关系等与试验保持一致。利用所编制的软件导入仪器舱段有限元模型,如图3所示。
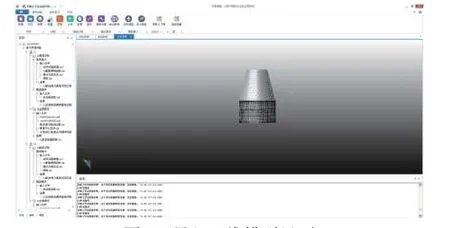
图3 导入三维模型界面Fig.3 Interface of imported finite element model
图4所示为曲线显示界面,其中蓝色曲线为试验功率谱密度曲线,绿色曲线为仿真功率谱密度曲线。

图4 曲线对比与显示界面Fig.4 Interface of comparative analysis of acceleration response curves
采用上述方法和软件预示的试验件噪声试验测点径向振动响应grms值与试验结果的对比如表1所示;考虑到有限元方法的适用范围,这里取10~1000Hz 的结果进行比较。
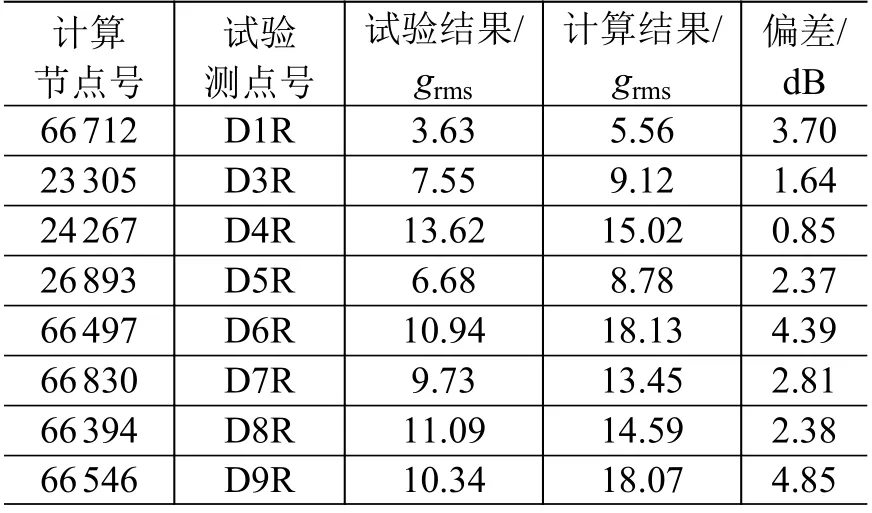
表1 测点径向振动响应计算结果g rms 值与试验结果的比较Table 1 Comparative analysis of the acceleration responses(g rms)
由于该舱段试验件为复合材料制成,所以准确模拟其阻尼及材料特性较为困难,而由图4及表1可看到,预示结果均大于试验结果,有3个测点的偏差在3~5 dB之间,其余5个测点的偏差均在3 dB 之内。在航天飞行器结构设计与试验领域,保守起见,适当的“过”比“欠”要好,因此该方法的预示结果有一定参考价值。
5 结束语
本文充分考虑声场载荷的空间相关性,解决了在有限元软件中真实声场载荷施加困难的问题,使仿真分析得到的振动响应更准确。该方法基于有限元分析方法,研制的软件可实现声场载荷加载、局部结构响应预示、响应提取及与试验测点响应的对比,误差在5 dB内,预示结果有一定参考价值。将该方法用于获取强噪声环境下航天结构动态特性和动态响应规律,可提高研制效率,为航天飞行器地面试验条件制定、结构设计与分析等提供有力的支撑。
