近空间连续流区航天器残骸解体分离落点散布数值预测研究
2020-10-31何跃龙喻海川孟旭飞李志辉
李 盾,何跃龙,刘 帅,喻海川,孟旭飞,李志辉
(1. 中国航天空气动力技术研究院, 北京100074;2. 中国空气动力研究与发展中心超高速空气动力研究所, 绵阳621000)
1 引言
航天发射活动在把航天器送入预定轨道的过程中,会生成大量尺寸较大的残骸及碎片,如燃料箱、整流罩、分离装置、航天器部件及助推器等。同样,服役期满大型航天器离轨陨落再入大气层过程,先后经历自由分子流区、过渡流区、滑移流区和连续流区,高速高温再入与空气发生振动、离解、复合等化学物理反应的真实气体力热效应,会致金属桁架结构响应变形软化熔融与复合材料热解烧蚀毁坏,进而发生解体产生大量碎片。 航天器解体过程所产生碎片,一部分会被继续熔融、烧蚀,剩余部分会撞击地面。 这些残骸碎片陨落区域可达横纵数十、数百或数千公里区域,并对地面人员、建筑及环境等造成巨大的威胁[1]。 准确预测航天器残骸碎片的再入飞行走廊,可有效避免或减轻这种危害。
服役期满大型航天器离轨再入-解体-陨落过程十分复杂,随着高度的降低,大气密度不断升高,航天器经较长时间的气动力/热作用,致结构响应烧蚀毁坏解体;解体分离阶段残骸碎片会存在显著的相互干扰;碎片脱离干扰区后,将各自自由陨落。 不是所有的陨落过程都包含以上各个阶段,如大气层内的发射活动将不存在再入解体过程;如果没有显著的气动力/热效应作用在航天器残骸上,也不会出现航天器毁坏、残骸烧蚀解体过程;对于超高速再入,残骸碎片在气动热积累作用下发生多次熔融、烧蚀解体的几率很高,存活碎片较少,残骸对地面造成的危险性也较低。
国内外关于航天器陨落再入分析预测及地面风险评估研究的方法,根据碎片再入预测模型可以分为2 类:面向物体法(研究对象为几种典型参数模型)和面向航天器法(研究对象为真实飞行器外形)[2]。
面向物体法中,将再入体复杂的几何结构简化为诸如球体、圆柱体、方形壳体等基本几何形状及其组合体[3],并且这些基本几何形状的信息都可通过相关的特征参数描述,典型的应用实例如NASA 的DAS[4]和ORSAT 软件,国内由清华大学和中国空间技术研究院共同开发的DRAPS[5-6]等。 面向航天器法中,作为研究对象的外形将会尽量真实地再现航天器原有的细节和结构,可以对航天器的气动特性等进行分析。 ESA 的SCARAB[7-8]是较为著名的面向航天器法工程软件。
每个民族大体上属于各自的国家,这个国家的政治体制、经济状态、军事军情、民俗风情、生活习惯都会在语言中有所表现。这种表现无不被民族文化所包含,形成各种类别的文化现象,比如政治文化、宗教文化、民俗文化、饮食文化等等。而当这些文化用语言进行表达时,经过翻译这一工具来置换,就出现了跨文化交际中词汇的盲区、多义、误解,甚至是由于延伸词意的不同带来麻烦。所以说,商务英语仅仅是专业英语的范畴,也不是掌握了专门的词汇和技巧就可以得心应手的,必须要和社会文化大环境的影响通盘考量。否则,不但影响了翻译内容的偏差,而且失去了作为商务英语的独特作用。
按照前面的分析,该线路的串联补偿装置安装位置应在整条线路电压降的中间位置,即电压为9.6 kV处,串入电容器的补偿度为1.25,此时,加入串补装置后,风孟线全线电压分布情况如图8所示。
本文仿真过程通过分别建立碎片静态气动数据库和动态特性数据库,实现对碎片大空域、宽速域陨落过程的仿真。 其中,静态气动数据库包含碎片在不同高度、马赫数、迎角、侧滑角等条件下的六分量气动力/力矩数据;动态特性数据库包含在对应条件下采用工程方法估算得到的碎片动稳定性导数。 在碎片陨落过程仿真中,根据碎片实时的弹道轨迹、当地风场条件等计算得到实时的高度、迎角、侧滑角等参数,并从2 个数据库中分别插值获得实时气动力及动稳定性数据,进而求解六自由度运动方程,可获得新的位置、姿态;重复该过程可仿真获得单个碎片陨落轨迹。 本文以整流罩的陨落模拟为例,简要介绍残骸碎片经过解体分离后彼此间不再有干扰,其运行轨迹可当作单体坠落进行处理,该残骸碎片落点预报仿真途径:
自来水出水桩采用水泥结构件进行组装,重量约280kg,占地面积0.3m2,出水桩由5部分组成:盖帽、支撑板、底座、水池座和水池。除水池用水磨石混凝土外,其他结构件均采用砂石混凝土内带冷拔钢丝网(结构如图1所示)。每部分都进行连接或配合,形成了一个完整结构。
本文利用CFD 中多体分离数值模拟技术求解残骸碎片解体过程,并在自由陨落过程综合静态气动数据库与动稳定性导数数据库实现对该阶段高效高精度模拟。 利用该方法对飞行试验中助推器的陨落过程进行仿真并与试验结果做对比,以验证方法的准确性和可行性。
2 数值方法
2.1 残骸碎片解体分离模拟方法
航天器陨落解体,残骸在近空间飞行环境高速陨落过程由于受到气动力/热作用,可能继续熔融、烧蚀、解体。 本文不考虑残骸的解体模型毁坏机理,仅将基于国家重点基础研究发展计划项目“航天飞行器跨流域空气动力学与飞行控制关键基础问题研究”形成的大型航天器跨流域气动力热/变形失效/热解烧蚀/解体飞行航迹数值预报平台生成的解体结果[13-14]作为输入,分析解体后的残骸碎片在气动力作用下的相互干扰分离过程。
对各处理中2017年全年茶青产量进行分析(图3),结果表明,随着施肥量的减少,F1、F2处理中茶青产量降低,CK处理中全年茶青产量为9082.28 kg·hm-2,F1处理中茶叶产量较CK降低4.6%,未达到显著性差异(P>0.05),F2处理中茶青产量显著降低(P<0.05)。配施有机肥处理中茶叶产量表现为 OF1>OF2>CK>OF3,OF1、OF2处理中,施氮量相等的情况下,OF1、OF2处理中茶青产量较CK分别升高13.28%、2.5%,处理间未达到显著性差异。
残骸的进一步毁坏解体分离计算,采用中国航天空气动力技术研究院自主研发的基于计算流体力学(CFD) 的多体分离过程数值模拟平台[15-16]。 计算网格采用非结构直角网格,针对近空间连续流区解体物绕流出现激波、剪切层等剧烈变化区域,采用自适应网格技术,以提升网格对流场结构的分辨率。 通过对流场结构的分析,使网格点分布与流场结构有效耦合,以较低的网格量实现对流场信息的准确描述,确保多体分离数值模拟的计算精度和流场分辨率。 物体运动过程由弹性动网格捕捉,随着时间推移若累积产生较大的相对位移,会造成计算网格质量下降,则通过网格的自动重构和流场插值,更新计算网格,如图1 所示。
流动对多体运动过程的影响通过求解ALE(Arbitrary Lagrange-Euler)形式的流动控制方程获得,为简单起见,式(1)列举考虑体积力的二维积分形式可压缩N-S 方程。

式中,

图1 网格弹性变形-重构过程示意图Fig.1 Illustration of the grid elastic deformation-reconstruction process
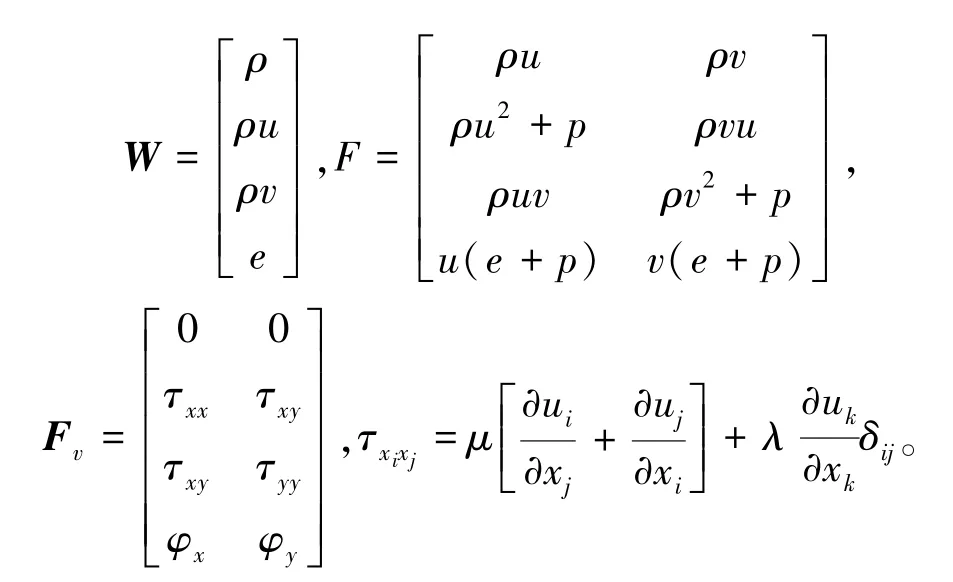
式中,变量ρ,p,e,T 和k 分别表示流体密度、静压、内能、温度和热传导系数; u,v 分别为速度矢量V 在直角坐标系下的速度分量;而根据Stokes 假设, λ =- 2μ/3;粘性系数μ 由Surtherland 公式给出。
1)首先采用CFD 方法获得整流罩在不同高度、马赫数、迎角(0°~360°)、侧滑角(0°~360°)下的完整气动参数数据库;
2.2 残骸陨落落区预报方法
2.1 节介绍的解体分离过程模拟方法适用于航天器解体残骸近空间飞行环境多次解体过程的模拟,解体一段时间后,各碎片间距离将逐步增大,之间干扰将逐步减弱直至消失,此时可以对各解体残骸碎片各自的陨落轨迹进行计算分析。 由于残骸碎片作为单体的陨落时间较长,进行完全的数值模拟将极为困难,本文通过蒙特卡罗仿真方法[12]分析多种因素影响下的陨落轨迹,进而获得碎片陨落区的预报结果。
在陨落过程中,碎片/残骸受到的气动力是影响落区散布的最重要也是最难模拟的因素。 在面向物体法中,气动力模型基于简化的物形给出,在考虑偏差、概率等因素影响后仍能获得较为合理的结果[9]。 应用面向航天器法时,通常是利用近似经验公式或CFD(Computational Fluid Dynamics)方法建立气动数据库[10-11],通过耦合六自由度动力学模型预测再入物体每一时刻的位置和姿态[12],这类方法预测精度高,但建模更复杂、需要消耗的计算资源也更多。
为了方便开展三维复杂外形动边界绕流计算,本文采用基于格心的有限体积法对控制方程式(1)进行离散。 使用线性MUSCL 格式对网格单元内流动变量进行重构,而单元面通量使用AUSM 系列格式或Roe 格式空间离散,时间离散采用隐式LU-SGS 迭代法。
2)在长时间仿真过程中,整流罩旋转的角速率可能出现非物理的增长导致姿态发散,在仿真过程中引入飞行器动导数可有效抑制角速率的非物理增长,保证仿真结果的稳定。 为了提高仿真效率,仿真前采用基于牛顿法的动导数工程算法对不同姿态、马赫数时整流罩动导数进行估算,得到动导数数据库;
3)整流罩在坠落过程中会发生复杂的姿态变化,进而导致其受到的气动力剧烈变化,根据地轴系下整流罩质心的运动速度、当地风场条件、整流罩的姿态可获得整流罩的实时迎角、侧滑角数据,进而从动导数数据库插值对应姿态的动导数、从气动参数数据库中插值得到整流罩的实时气动力数据;
综上所述,利用落锤、霍普金森杆实验平台和液压介质产生的动态脉冲载荷,峰值较高。但脉宽缺少10~102μs量级。本文设计了一种半正弦波脉冲载荷发生装置,可产生压力载荷峰值达50 MPa,脉宽为10~102 μs,可应用于实验室内进行冲击动力学加载实验。
阀板式进水口优点:相比传统转盘水阀,阀板式进水口通过打磨平顺沉箱进水口位置,在沉箱下潜时由于沉箱内外水头差,外水压通过橡胶垫板压紧沉箱进水口,密封性能好。在沉箱出驳安装施工时,以往传统水阀进水控制全靠潜水员进行控制,需要配备数个潜水员下水拧紧或拧松转盘进行开关控制进水,程序较为复杂,且容易导致每个格仓水量不一致。而阀板式进水口,只需要在进水口相应的位置沉箱顶上安排人员进行拉绳或松绳操作,在技术人员的控制口令下,立即能进行沉箱进水量控制,操作简单便捷,控制压载水速度快,沉箱格仓压载水量平衡,沉箱调平效果好,且不需要潜水员进行潜水作业。
1.2.3 培训内容 针对问卷调查的结果,确定相应的培训内容。主要为:①腰背痛产生的原因、预防、锻炼。②力学的原理,节力原则及运用。③正确的各种预防腰背痛发生的姿势、各项正确的护理操作。
4)根据整流罩所受气动力、气动力矩以及整流罩质心运动速度、旋转角速度等参数,通过数值方式求解刚体六自由度运动方程可获得新的质心位置、整流罩姿态以及整流罩运动的速度和旋转角速度;
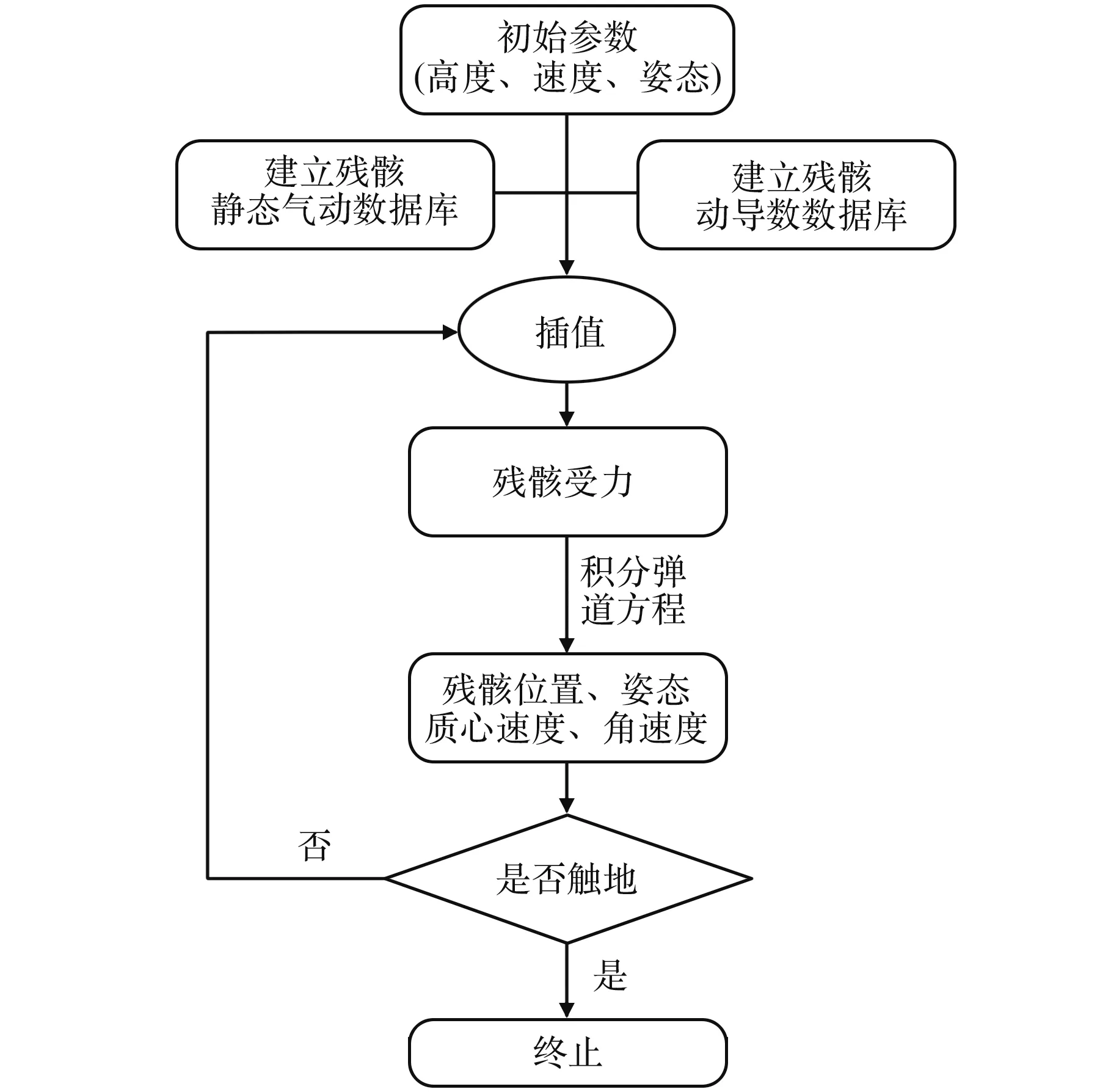
图2 落点预报流程图Fig.2 Flowchart of the falling point forecast
基于上述过程,根据初始参数的不同,考虑参数拉偏、初始条件的随机分布等影响,可仿真获得最终的残骸碎片陨落区预报结果。
3 陨落过程仿真及结果
首先以近空间助推器自30 km 高空以不同迎角、侧滑角和马赫数为初始条件、陨落过程仿真模拟结果与飞行试验数据比较验证基础上,采用上述方法分别对整流罩左、右两部分陨落及航天器再入解体、进入近空间飞行环境多次解体分离陨落过程进行仿真分析,以示意整个陨落区预报过程。
在进行农机推广过程中,很多的企业都将机械设备的重点放在粮食的生产过程中,而对于这方面农业机械设备的技术也在不断的创新研究。但是在实际的应用中,对于农副产品的加工等问题也需要先进的农业机械设备进行完成的,并且一些地方特色的农产品对机械设备的要求更加严格。因此针对这种情况,导致农业机械设备的推广体系必须要加强完善,要让农民能够及时的了解各种特殊机械设备的性能,从而使农机推广水平得到有效的提高。
3.1 近空间飞行环境助推器陨落模拟与验证
助推器部件级在大气层内的陨落过程是高空残骸陨落的重要研究对象。 对某飞行试验中助推器部件级的落区散布问题进行模拟分析。 图3 所示为仿真分析的助推器模型,陨落初始条件为高度30 km,速度约1700 m/s,弹道倾角0°。

图3 助推器部件级陨落仿真模型Fig.3 The simulation model for the booster falling forecast
开展这类近空间连续流区的单体无控陨落落区预报时,首先建立助推器静态数据库和动稳定性导数数据库,数据库主体参数范围为:迎角0°~360°,间隔2°;侧滑角0°~360°,间隔1.5°;马赫数取0.4、0.9、1.2、2.5、4 和6 共6 个样本;气动导数数据库迎角、侧滑角和马赫数样本选取与静态气动数据库相同。 仿真时考虑了马赫数、高度、迎角、侧滑角、弹道倾角等参数的初始偏差和2 组数据库的精度偏差。 迎角、侧滑角对助推器以不同马赫数陨落的落点散布。
图4 绘出了不同迎角、侧滑角设置下助推器以不同马赫数陨落的落点散布情况,可看出落点位置沿射向分布与初始迎角有一定相关性。 在其他初始条件相同的情况下,随着迎角的增大,初始阶段残骸受到的阻力越大,减速越明显,导致残骸沿射向距离越小。 初始侧滑角对落点沿侧向的分布影响明显,模拟结果发现:不同侧滑角条件下仿真获得的落点具有明显的分块集聚特性。
5)重复步骤3、4,直至整流罩落到地面,获得陨落过程的整流罩轨迹参数,完成单条整流罩落点预报(图2)。

图4 助推器陨落的落点散布结果Fig.4 The forecasted booster falling spot distribution
为验证本文提出的模拟策略,在上述仿真预报基础上,进行该助推器自30 km 的陨落飞行试验,通过雷达图像跟踪测量,获得了助推器部件级的陨落飞行空间位置速度数据,图5 绘出了采用本文方法仿真得到的基准态助推陨落过程沿射向速度和射程数据(绿色-三角符号曲线)与飞行试验结果(红色圆点符号曲线)对比情况。 由图5对比分析可以看出,本文仿真预报结果与最终飞行试验结果吻合较好,证实本文基于气动力数据库支撑的弹道飞行航迹落区计算模型高精度可靠性。
产品外观设计的内容会直接影响到产品外观设计的质量,因此,应严格规划产品外观设计的具体内容。将传统图案应用在产品外观设计中是体现中华民族文化和弘扬传统文化精神的重要表现形式。在多元化的市场环境下,重视产品外观的文化特色并与传统图案中的民族元素进行有效融合,可使产品在激烈的市场竞争中继续保持竞争优势。
《方案》进一步明确,坚持幼儿为本,坚决纠正幼儿园“小学化”的违规办园行为。禁止幼儿园提前教授汉语拼音、识字、计算、英语等小学课程内容。幼儿园不得布置幼儿完成小学课程内容家庭作业,不得组织小学课程内容的有关考试测验。坚决纠正幼儿园以课堂集中授课方式为主组织安排一日活动;或以机械背诵、记忆、抄写、计算等方式进行知识技能性强化训练的行为。整治“小学化”教育环境,解决教师资质能力不合格问题。
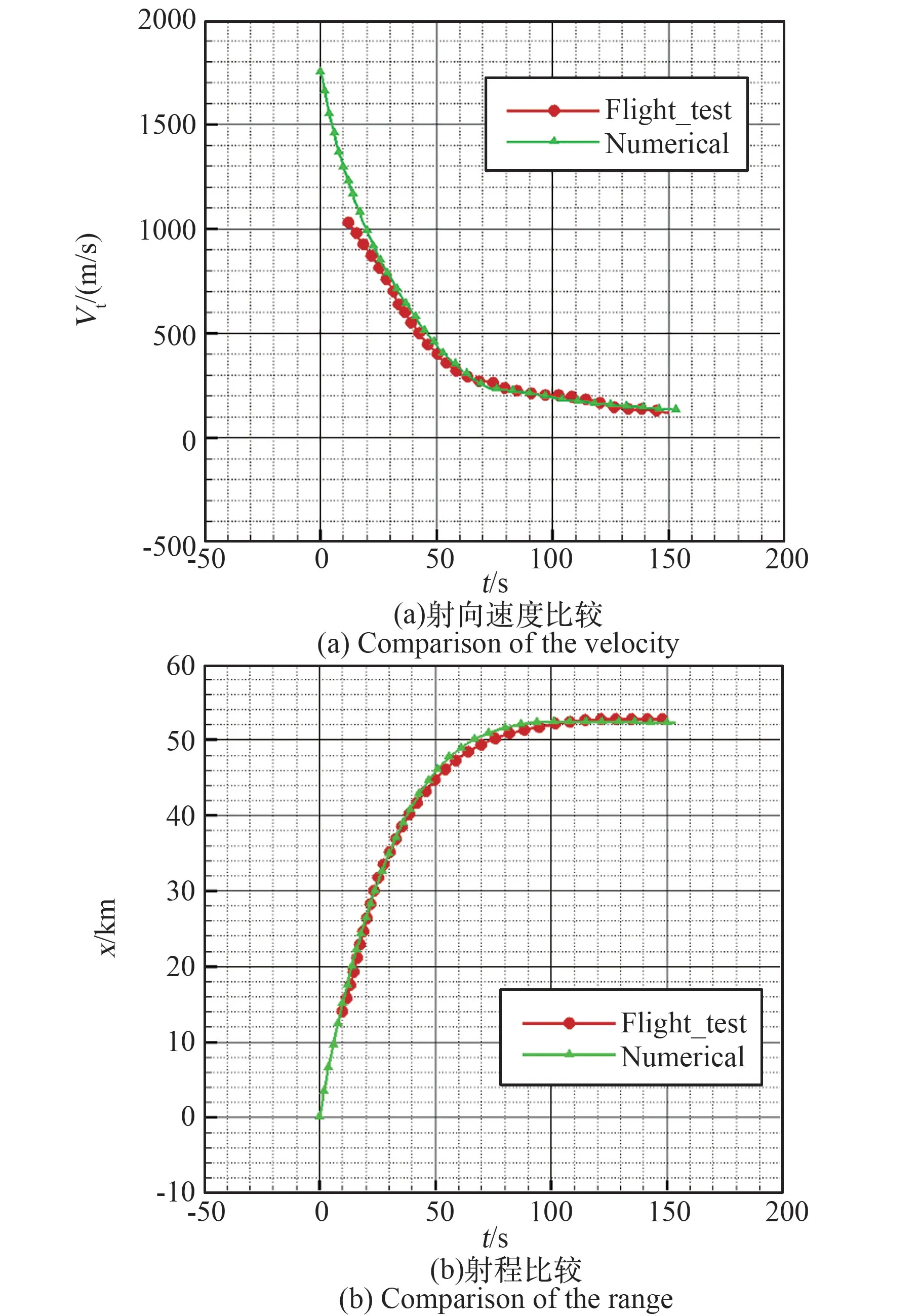
图5 助推器陨落预报结果与飞行试验数据对比Fig.5 Comparison of the booster falling forecast and flight test data
3.2 整流罩陨落模拟分析
对典型的整流罩陨落轨迹进行分析,图6 所示为整流罩外形图,图中2 片半罩前端外形有一定差别,图6(a)所示左罩有一个鼻锥,图6(b)所示右罩为开口形态,两罩组合可形成完整的整流罩结构。 两半罩从30 km 高度陨落,初始时刻两者存在一定的侧向分离速度和角速度。

图6 整流罩外形图Fig.6 The configuration of the fairings
建立气动数据库时迎角在0°~360°范围变化,间隔30°;侧滑角0°~360°,间隔15°;马赫数取0.4、0.8、1.5、2.5、4 和6 共6 个样本。 气动导数数据库迎角、侧滑角和马赫数样本选取与静态气动数据库相同。
图7 为两半罩典型陨落轨迹示意图,图中给出的轨迹考虑了风场、气动阻尼等因素影响,但没有考虑气动偏差的影响。 两罩分离后沿x 方向飞行30~40 km,在陨落末段出现了明显的拐点,半罩飞行速度偏离初始陨落阶段速度,甚至出现了向相反方向飞行(掉头)情况。 主要是由于在陨落末端,整流罩飞行速度主要是沿竖直方向,其在横侧向的分量较小,因此可能在侧风影响下出现这种偏离现象。
图8 绘出了两罩陨落过程中飞行马赫数、海拔高度等参数变化过程。 在陨落初期,整流罩飞行速度在气动力作用下急剧降低,在几十秒时间内即降到亚声速飞行。 在陨落末段以低于0.3 马赫的速度飞行近200 s 的时间,最终落地。 在从超声速段向亚声速段过渡后,整流罩陨落飞行高度随飞行时间变化曲线也出现明显的拐点,陨落体在近空间高速陨落时空气动力作用显著,导致陨落体在极短时间就从高超声速减速到亚声速,其后因速度、能量进一步降低,在稠密大气层出现飘落飞行过程,致马赫数、高度随时间变化曲线出现类似拐点缓慢飞行下降的过程。
为了模拟陨落体的落区散布范围,采用蒙特卡罗方法进行仿真分析,通过对相关参数拉偏获得偏差量,来跟踪模拟可能对最终落点影响情况。本文选取的偏差量按照标准正态分布随机选取获得的随机数作为随机偏差系数,与常系数ε(10%、20%或30%)相乘作为最终的偏差系数。
每个半罩分别仿真了5 种不同的初始状态、设置3 种不同的气动偏差,共计15 组状态,每一组仿真了600 个样本点,以统计各种拉偏对落点的影响规律。 图9 所示为考虑偏差时左/右罩落点分布,每个半罩都仿真了9000 个样本点。 图中不同颜色标识的是采用不同拉偏幅度时仿真得到的落点位置,黑色圆点表示不同初始条件下不考虑偏差影响时的落点位置。 从图中落点分布可以看出,考虑偏差时各样本点位置基本分散在不拉偏时各落点附近,大部分落点位置相对集中;采用不同拉偏幅度仿真的落点分布基本一致,没有出现明显的因为拉偏幅度增大而落点范围变大的情况,证实所发展残骸落区预报方法的强收敛可靠性。 图9 中红色框线给出了仿真结果主要积聚区域(包含了仿真结果中99%以上的落点),左罩预测落区沿射向为32 ~42 km,侧向-9 ~1 km;右罩预测落区沿射向为25~40 km,侧向-8~3 km。
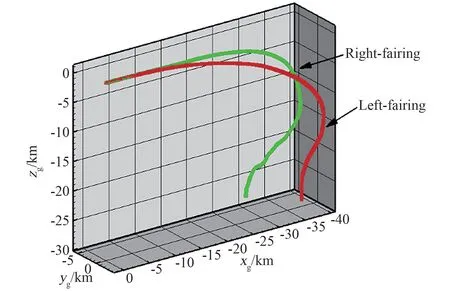
图7 两半罩自30 km 高度典型状态陨落轨迹Fig.7 Typical falling trajectory of the fairings from 30 km
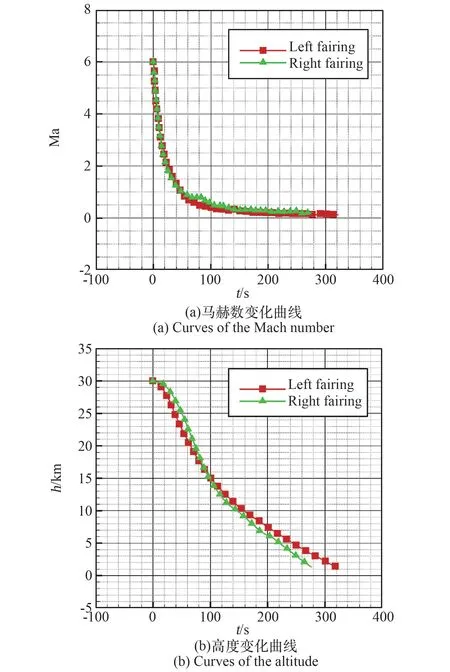
图8 典型状态整流罩陨落过程Fig.8 Typical fairing falling process
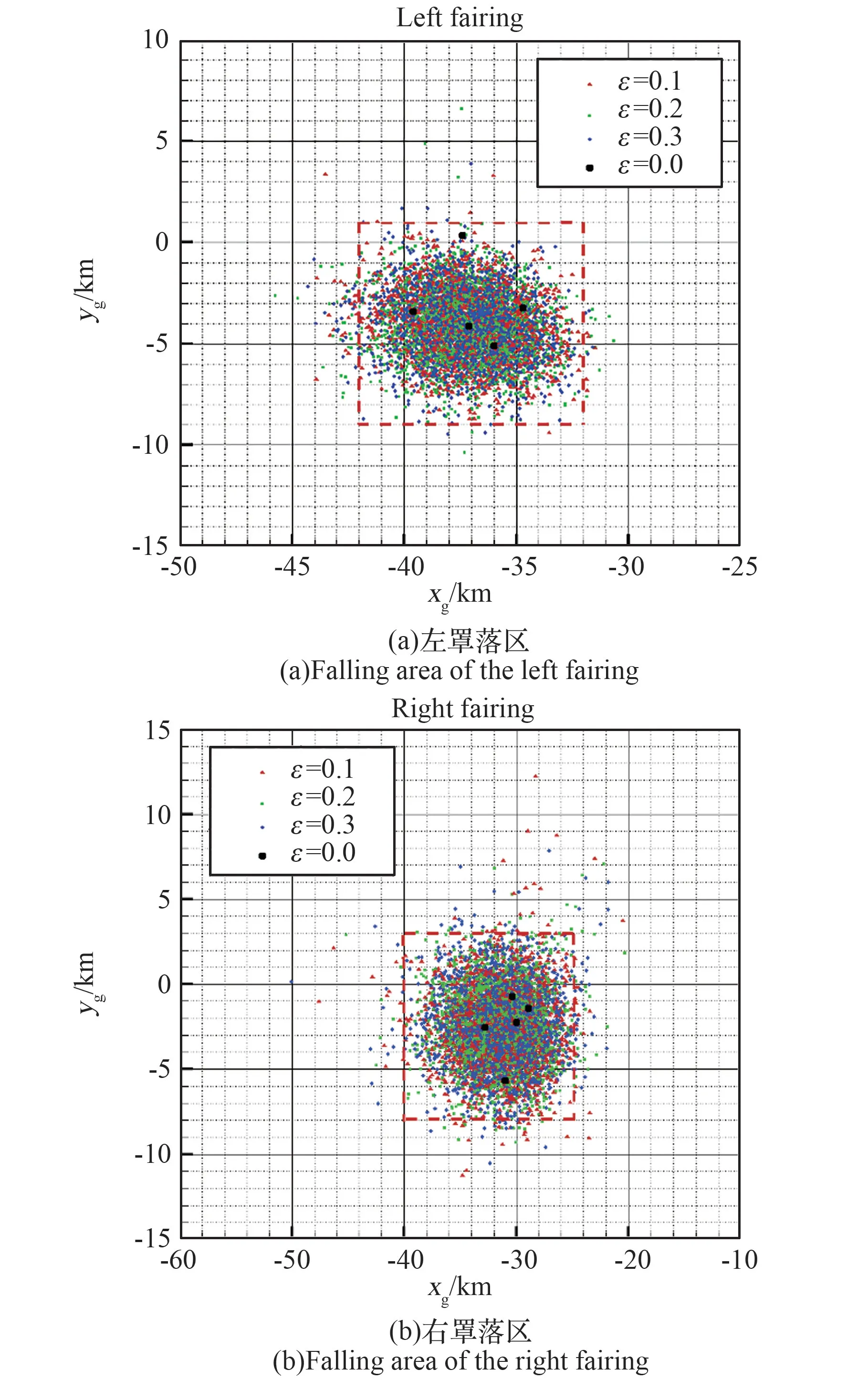
图9 左右两半罩落区分布预报结果Fig.9 Forecast of falling area of left and right fairings
3.3 航天器解体分离
大型航天器再入解体进入近空间飞行环境以及航天器自高空高速陨落,都可能在极端的气动力热条件下产生毁坏解体情况,解体后碎片在气动力作用下发生相对运动,并逐渐分离,呈现各自的陨落飞行。 本节对典型的航天器解体分离过程进行模拟分析。
目标飞行器如图10 所示,设定飞行器解体后分解为8 个部件,各自以一定初始速度、角速度做解体分离运动。 图11 所示为计算过程中某时刻对称面网格划分示意图。
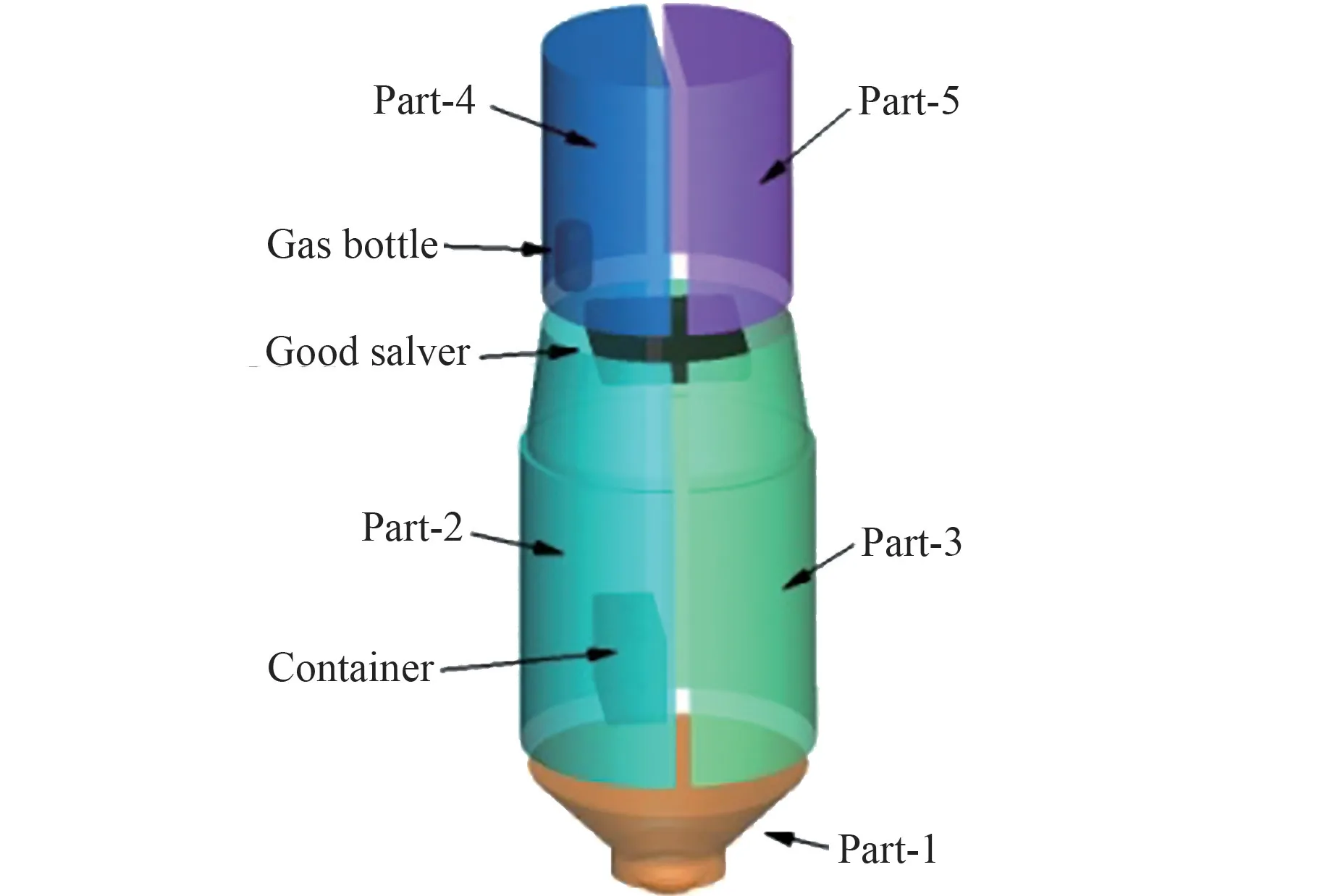
图10 航天器模拟解体分离计算模型Fig.10 Calculation model for spacecraft disintegration and separation simulation
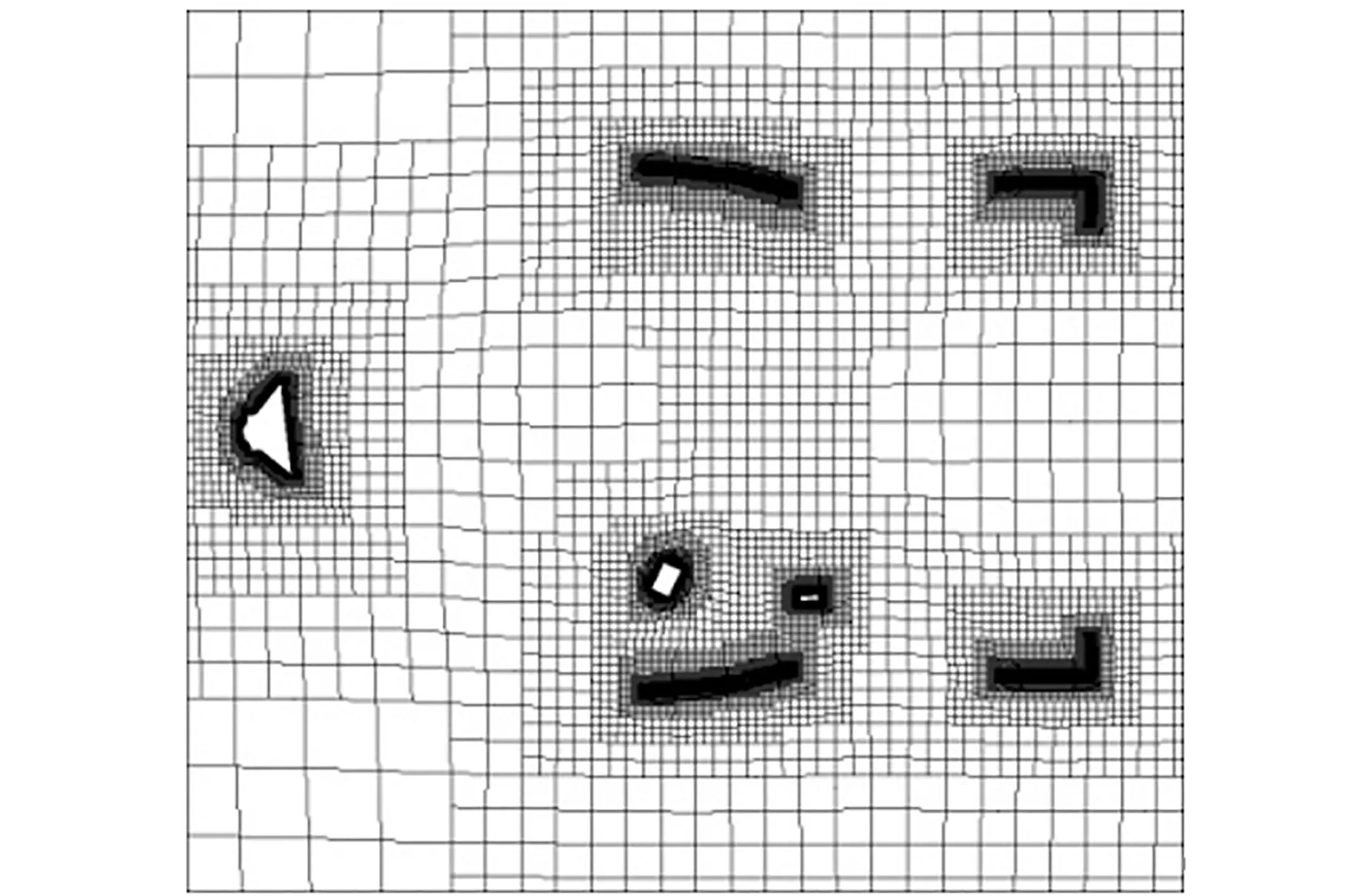
图11 某时刻对称面网格示意图Fig.11 Diagram of symmetrical plane grid at an instant
图12 绘出该目标航天器解体分离过程图像。在数值模拟中,由于考虑的部件数目较少,且根据初始分离力给出初始速度、初始角速度较大,因此没有出现相互碰撞等情况,分离过程中各部件以各自的速度向外飞行。 当解体分离过程持续一段时间后,各部件间相互干扰将逐步减弱,各碎片的运动可以看成各自独立的陨落过程。 此时,可以将脱离干扰区的碎片位置、姿态、运动速度、角速度等作为初始条件(或输入条件),进行后续碎片陨落散布区域预报仿真。
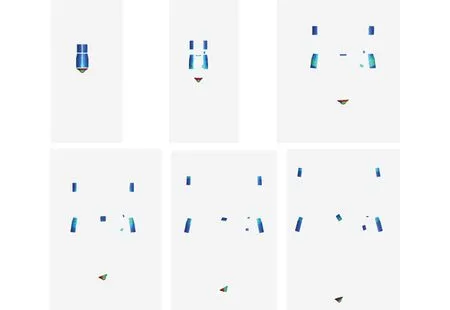
图12 航天器解体分离过程模拟结果Fig.12 Simulation of spacecraft disintegration and separation process
4 结论
本文基于非结构直角网格系统,采用弹性变形-重构耦合的动网格技术捕捉复杂运动过程,结合自主研发的非定常CFD 数值方法,实现了有气动干扰的多体碎片动态分离过程的数值模拟。针对无干扰情况下残骸碎片自由陨落过程,发展了基于静态气动数据库和动态稳定性导数数据库仿真技术,建立了近空间飞行环境航天器残骸解体分离过程数值模拟方法。
采用文中方法对近空间飞行环境航天器解体分离、助推器及整流罩自30 km 高度陨落预报开展仿真,通过其中助推级射向速度、射程数据与飞行试验数据对比验证,证实了本文所建立仿真方法正确可行。
