大型航天器无控飞行再入时间短期预报的轨道摄动方法研究

2020-10-31高兴龙李志辉彭傲平

载人航天 2020年5期

高兴龙，李志辉，陈钦，丁娣，彭傲平

(1. 中国空气动力研究与发展中心空气动力学国家重点实验室，绵阳621000；2. 中国空气动力研究与发展中心设备设计及测试技术研究所，绵阳621000；3. 中国空气动力研究与发展中心超高速空气动力研究所，绵阳621000；4. 北京前沿创新中心国家计算流体力学实验室，北京100191；5. 中国空气动力研究与发展中心计算空气动力研究所，绵阳621000)

1 引言

大型航天器寿命末期离轨再入大气层时一旦功能失效，只能由受控再入转为依靠无控飞行轨道衰降再入，无控再入的大型航天器通常由于自身系统如对地通信等故障造成失控，最终自然陨落再入大气层解体，残骸碎片坠落地球。历史上大型航天器失效后再入大气层的案例较多，如美国的Skylab 空间站[1]。大型航天器寿命终止后离轨自然陨落，将在低地球轨道环境气动力/矩和地球引力[2]等摄动因素影响下，轨道高度逐渐衰降至最终再入大气层[3]。当缺少导航信息或信息服务数据中断时，需要独立依靠轨道动力学模型对航天器的轨道飞行航迹进行计算预报，尽可能地实现航天器空间位置速度状态的可行性预测。预报初值轨道参数精度和动力学模型精度直接影响航天器星历预报精度。数值积分法利用确定的初值逐步递推航天器的位置速度或瞬时轨道根数，可以充分考虑各种摄动因素的影响，对于短期的高精度轨道预报较适用。

李志辉等[4-5]的研究表明，空气动力对低轨航天器的轨道预报影响显著，低地球轨道环境大型复杂结构航天器的气动力随高程显著改变，如300～200 km 变化幅度达8%～50%。即使考虑5%的阻力偏差，低轨空间目标的24 h 位置计算精度最大预测偏差可达64 km[6]。而且李志辉等[4，7]的初步研究表明，对低地球轨道环境无控航天器的轨道衰降模拟，必须充分考虑目标飞行器轨道衰减过程所受到的跨流域空气动力特性随飞行姿态变化影响。同时大部分非受控再入航天器都处于姿态失稳飞行状态，研究寿命末期大型航天器在低轨甚至超低轨道情况下的轨道动力学特性，需要同时考虑飞行器姿态的影响[8]。 Hart等[9]利用解析的自由分子流气动模型开展了低轨空间目标的快速轨道外推和不确定参数敏感性分析，并对目标在轨寿命进行了预测。 Sommer等[10]对中国天宫一号再入过程的姿态运动和截面积进行了分析。 Nazarenko[11]利用双行根数(Two-Line Element，TLE)轨道数据考虑随机大气环境扰动对天宫一号的再入时刻进行了预报研究。

轨道预报精度的误差因素主要来自定轨初值误差和动力学模型误差，通常需要依靠滤波参数辨识方法尽可能消除误差因素的影响，提高预报精度。郑作亚等[12]将无迹卡尔曼滤波(Unscented Kalman Filter，UKF)算法应用在GPS 卫星轨道的短期预报中，有效提高了轨道预报精度和稳定性。

传统的基于常值阻力系数及数据拟合的气动参数的预报方法在轨道预报问题上没有充分考虑姿态变化引起的空气动力的影响，因此需要结合姿态和跨流域气动环境将更高精度的气动特性建模方法融合进轨道动力学模型中。为此，本文基于稀薄跨流域空气动力数值模拟驱动设计的大型航天器气动特性当地化快速算法，求解目标航天器不同高度和飞行姿态对应的气动力、力矩系数，建立气动融合姿态动力学轨道摄动模型，结合UKF 算法消除外测轨道星历数据和数值积分误差影响，对大型航天器进行短期的轨道外推计算预报。

2 轨道-姿态摄动模型

2.1 参考坐标系

无控航天器的轨道预报需要考虑姿态变化所引起的气动力以及气动力矩系数的变化，从而充分考虑姿态变化和气动力因素对轨道摄动的影响。如图1 所示，建立轨道坐标系Obxryrzr，本体坐标系Obxbybzb，速度坐标系Obxvyvzv和地心惯性坐标系Oxyz，描述航天器位置速度和姿态的变化。

图1 参考坐标系示意图Fig.1 Sketch of reference frames

2.2 动力学模型及假设

目标航天器的轨道摄动方程由J2000 地心惯性坐标系下的位置和速度矢量描述，姿态描述为了避免奇异问题，采用四元数的方式，应用姿态四元数与方向余弦的关系，可得到姿态四元数的运动方程[13]，则目标航天器六自由度动力学方程具体形式为式(1)。

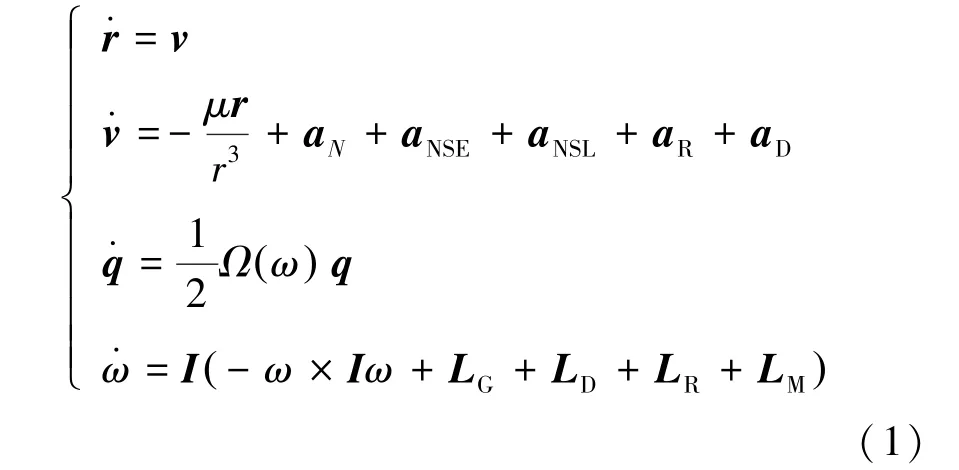
式中， r ＝ x，y，z[ ]T为位置矢量， v ＝[ vx，vy，vz]T为速度矢量，q ＝ [q1，q2，q3，q4]T为轨道系到星体系的四元数，ω 为航天器的姿态角速度；μ 为地球引力常数， I 为航天器的惯量矩阵。摄动加速度项分别是: aN为N 体引力摄动加速度，本文考虑日、月的引力摄动加速度； aNSE为地球非球形摄动加度，是低轨航天器的主要摄动因素，本文计算采用精度较高的JGM-3 地球引力位模型；aNSL为月球非球形摄动加速度； aR为太阳光压摄动加速度；aD为J2000 地心惯性坐标系下的大气阻力摄动加速度，可由体坐标系下的加速度aB经过坐标转换得到，如式(2)所示。

式中，Bq为四元数的方向余弦矩阵， BOJ为轨道坐标系到地心惯性坐标系的转换矩阵，aB可以根据气动力系数写成体坐标系下的三分量形式，如式(3)所示。

式中:CA、CN和CZ分别为目标航天器的轴向力系数、法向力系数和侧向力系数，Sref为目标航天器阻力无量纲系数参考面积，ρ 为大气密度，本文采用NRLMSISE00 大气密度模型计算，Vr为航天器相对于大气的运动速度，可以写成式(4)。

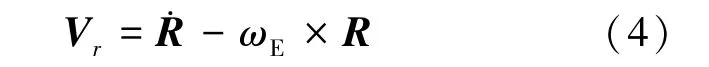
式中，ωE为地球自转角速度。

式(1)中右端的扰动力矩分别是:LG为重力梯度力矩，LR为太阳光压力矩，LM为地磁力矩；LD为气动扰动力矩，若记滚转力矩系数为Cl，俯仰力矩系数为Cm，偏航力矩系数为Cn，参考面积为Sref，参考长度为Lref，同样可根据气动力矩系数将LD写成体坐标系下的三分量形式，如式(5)所示。

3 航天器跨流域气动特性一体化快速计算

大型航天器的气动力系数随轨道高度和姿态的变化显著，在轨道预报过程中，需要根据航天器再入过程的快速响应，考虑气动特性计算的高效性。如天宫一号目标飞行器，低轨道飞行过程是一个自数百到数十量级Knudsen 数高稀薄自由分子流动状态多物理场复杂构型极高超声速流动问题[14-16]。为了捕捉空气动力特性对轨道衰降过程影响，本文使用文献[5]与文献[17]发展的当地化快速算法，分别在高度区域[250 km，200 km]、[200 km，120 km]、[120 km，100 km]每间隔5～3 km、2.5 km、2 km 各典型绕流状态，使用跨流域空气动力学数值方法计算，结果作为各子区域边界值[4-5，18]。而对于连接各子区域边界的中间过渡区，采用修正的Boettcher/Legge 非对称桥函数理论[17]，发展可分段描述的非对称压力与摩擦力系数关联桥函数，在给定的物面角θb，当地面元上的压力和摩擦力系数分别为式(6)、(7)。

式中，Fb，p和Fb，τ分别是压力和摩擦力桥函数，依赖于独立参数Kn、Tw/T∞和θb。

对于类天宫一号目标航天器可用三角形非结构网格表征其飞行器物形，采用通用近似的面元法对航天器进行物形处理，当面元划分足够细小时，引起的误差就更小[19]，由此形成低轨道跨流域气动力特性一体化快速计算技术。在高稀薄自由分子流区，可采用基于不同模型材料修正的Nocilla 壁面反射模型进行压力系数和摩擦力系数计算，在Maxwell 平衡态气体分子速度分布的假设下，每个面元的压力和摩擦力系数为式(8)、(9)。

式中，Tw、T∞分别为物面和来流温度，σN和σT分别为法向和切向物面动量适应系数， erf()为误差函数，s 为速度比，定义为式(10)。

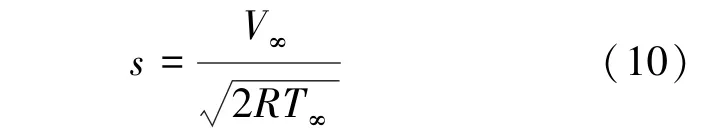
式中，R 为通用气体常数。

由此，充分利用高性能计算机开展DSMC 和求解Boltzmann 模型方程统一算法对相关关联参数进行调试确定和计算修正，最终获取适用类天宫一号目标飞行器覆盖跨流域不同飞行高度和典型姿态的气动力和力矩。图2 所示为计算得到的在350～100 km 高度下，航天器气动阻力系数随高度变化曲线。从图中的阻力系数变化趋势可以看出，350～180 km 轨道高度范围的阻力系数缓慢减小，之后随着轨道高度的降低，阻力系数剧烈下降，这种异常现象主要是由于跨过该高度，气流密度、动压迅速呈量级增加，致大气阻力系数迅速减小，虽然大气阻力有量纲量随飞行高度降低呈现非线性增大。图3 为目标飞行器轴向力、法向力和俯仰力矩系数随迎角变化曲线。

图2 类天宫一号目标飞行器轨降过程气动阻力变化Fig.2 Changes of aerodynamic drag characteristics of Tiangong-1-type spacecraft with altitude during the orbital decline process

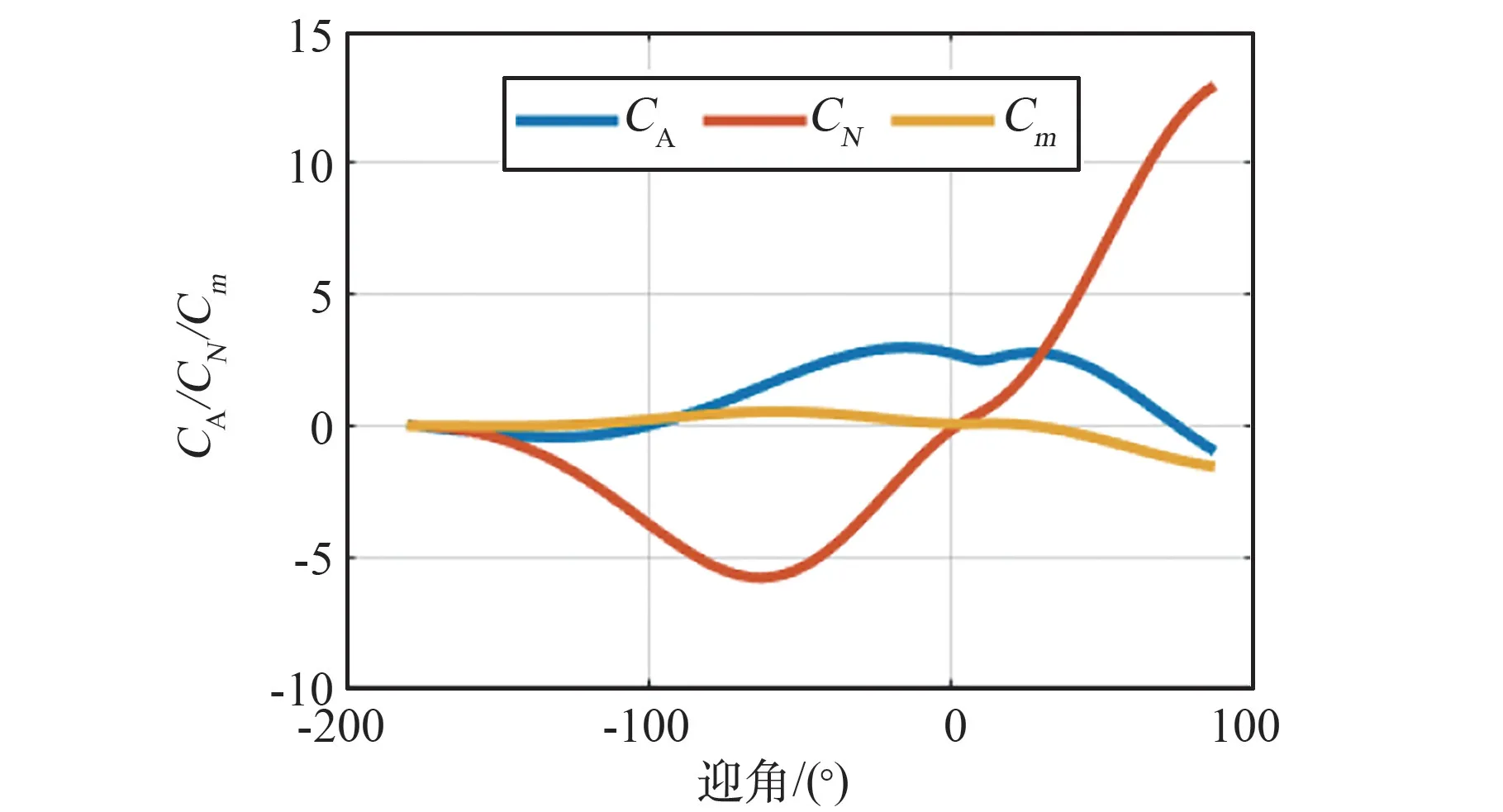
图3 类天宫一号目标飞行器轨降过程轴向力、法向力和俯仰力矩系数随迎角变化曲线Fig.3 Changes of axial， normal force and pitch moment coefficients of Tiangong-1-type spacecraft with angle of attack during the orbital decline process

4 UKF 算法与状态估计

利用初始外测目标飞行器轨道信息，直接积分轨道姿态动力学模型，同时根据预测状态信息可以确定对应高度和姿态的气动系数。依次顺序迭代计算。同时结合UKF 思想，开展数据滤波，得到对航天器位置速度和姿态的跟踪结果。首先将位置、速度矢量的轨道参数和四元数、角速度矢量的姿态参数定义状态量x 为式(11)。

同时将该问题以状态方程、输出方程和测量方程的形式表示如(12)所示[20]。

式中， x 为状态向量，对应目标航天器的位置、速度、姿态角和角速度，y 为观测向量，u 为系统的输入，对于无控的目标航天器u ＝O；z 为外测得到的离散时间序列，包含测量误差。 F 和G为过程和测量噪声附加矩阵。通过测量结果z 来对x 进行跟踪和估计，采用UKF 算法对上述方程进行处理。在UKF 算法中，对于非线性系统的状态估计问题，其状态随机变量需要定义成原状态量和过程、测量噪声随机变量的组合，即式(13)。

这样系统扩展成L 维空间，相应的状态协方差矩阵可写成[21]式(14)。

式中， Px为状态量的协方差矩阵， Rw和Rv为过程和测量噪声协方差矩阵。与EKF 算法相比，UKF 具有二阶精度，且不需要计算Jacobian 和Hessian 矩阵，使得算法更易实现，并可用于不可微函数估计。

无迹变换(Unscented Transformation，UT)是无迹卡尔曼滤波的核心[21]，它通过构造有限样本点(sigma points)来近似随机变量在非线性变换下的统计特性。比例无迹变换(Scaled Unscented Transformation，SUT)是在UT 的基础上加入比例系数，用于在协方差矩阵保持正定的状态下对样本点进行调节。基于SUT 变换的标准UKF 算法可分为预测和矫正两步进行，算法流程如下:

1)初始化。由先验信息给出状态量估计和协方差，假设噪声信号为零均值白噪声。

2)构造采样点。由SUT 变换构造2L＋1 个采样点，即式(15)。

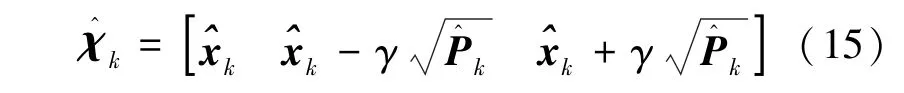
引入系数γ，其表达式为式(16)。

3)预测。由k 状态预估第k＋1 步的状态量及均方差如式(17)所示。

4)校正。由观测量对预测量进行校正，首先计算增益矩阵K，由状态量估计值可给出输出量估计及协方差矩阵，然后由协方差矩阵计算增益矩阵，再由增益矩阵对系统状态量和协方差矩阵进行校正。若噪声为累积白噪声，则可去掉过程和测量噪声。

与EKF 算法相比，UKF 具有二阶精度，且不需要计算Jacobian 和Hessian 矩阵，使得算法更易实现，并可用于不可微函数估计。

该方法可以克服直接积分六自由度动力学模型长时间所带来的误差积累、长时间预报精度降低的问题，同时可以显著提高计算效率，便于对轨道和姿态动力学模型分别进行误差分析。

5 无控航天器轨道摄动模型仿真结果

利用前文所建立的数学模型和滤波方法对类天宫一号目标飞行器的无控飞行轨道变化进行计算验证，图4～图7 为预测的该目标飞行器轨道根数和姿态变化。计算时间取4.5 天，观察其变化趋势。图4 为类天宫一号目标飞行器轨道高度衰降变化曲线的仿真结果与TLE 观测数据的对比结果，从初步的计算结果可以看出，轨道预测的仿真结果与观测结果相符。图5 为轨道根数变化曲线，可以进一步看出目标飞行器临近再入前几天的轨道变化趋势。

图4 类天宫一号目标飞行器轨道高度变化Fig.4 Altitude variation of Tiangong-1-type space-

图5 类天宫一号目标飞行器轨道根数变化Fig.5 Orbital elements variation of Tiangong-1-type spacecraft

从图6 和图7 的结果可以看出，目标飞行器姿态角和角速度的参数变化具有一定的随机性，当前的测量手段还无法对无控大型航天器的姿态变化参数给出较精确的估计结果。本文通过算例初步验证了考虑姿态变化关联气动参数方法的可行性，未来还需要结合随机理论和统计学方法进一步分析大型无控航天器姿态变化对轨道预报精度的影响，完善气动融合轨道数值预报方法的技术手段。总之，本文计算得到的轨道和姿态变化的预测结果均与测站偶尔观测理论预期吻合相容，尤其是姿态动力学积分计算收敛、结果合理。

图6 类天宫一号目标飞行器姿态角速度变化Fig.6 Attitude angle velocity variation of Tiangong-1-type spacecraft

图7 类天宫一号目标飞行器姿态角变化Fig.7 Attitude angle variation of Tiangong-1-type spacecraft

6 轨道预报精度分析

将经气动融合参数辨识摄动模型计算得到的轨道预报数据与目标航天器实际观测数据所获取的轨道星历信息进行对比，分析不同时刻的计算误差，得到地心惯性坐标系下的位置矢量偏差和平均轨道高度偏差随时间推进的变化趋势，如表1 所示。

表1 无控航天器轨道预报精度Table 1 Orbit prediction accuracy of uncontrolled spacecraft

气动力作为非保守力是引起目标航天器轨道形状和大小改变的主要摄动因素之一。从误差分析结果可看出，24 h 内的位置矢量偏差最大约为30 m，平均轨道高度偏差最大约为16 m，实际目标航天器的轨道高度在平均轨道高度上下做周期性运动；从计算精度变化趋势来看，误差都是随着时间推进先增大后逐渐收敛，计算偏差的收敛有助于提高模型预报的精度，证实本文提出研究建立经卡尔曼滤波误差分析与参数辨识的气动融合轨道摄动模型方案，对无控航天器轨道衰降模拟正确性有较强模拟能力。