最小二乘无网格方法及其在近空间解体碎片绕流场模拟应用

罗万清，梁剑寒，李海燕，李志辉，3*

(1. 国防科技大学高超声速冲压发动机技术重点实验室，长沙410073； 2. 中国空气动力研究与发展中心超高速空气动力研究所，绵阳621000；3. 国家计算流体力学实验室，北京100191)

1 引言

空间碎片是指在发射火箭、卫星等飞行器执行太空任务后产生的火箭箭体、卫星本体以及航天器在轨执行航天任务过程中产生的抛弃物、太空中物体之间碰撞产生的碎块等。 特别是诸如天宫一号目标飞行器超期服役两年半突发功能失效，面临无控飞行、轨道衰降、再入坠毁，飞行航迹预示，大部解体会在再入环境强气动力/热作用下熔融/烧蚀，至少10%～40%的残骸碎片坠落地面[1]。 为此，发展准确求解近空间多次解体非规则残骸碎片间绕流干扰问题的数值计算方法[2]，成为数值预报落区散布范围的重要途径。

数值方法种类很多，如有限差分法、有限体积法、有限元法以及谱离散法等，这些方法在模拟流动时首先对流动区域进行网格离散，然后将需要求解的流动方程在空间网格上进行离散，进而求解得到流动区域内的流场参数[3-4]。 基于此，空间离散网格对计算效率和结果可靠性有重大影响，在网格生成时不得不同时考虑网格数量、网格正交性、疏密分布等。 由于在实际工程问题中存在大量具有复杂几何外形的流动，如航天器再入近空间多次解体非规则残骸碎片间绕流相互干扰，或者具有运动边界的复杂流动，既计算高效又保证结果准确地求解这些复杂问题至今仍是计算流体力学的难点[5]。无网格方法采用基于点的近似原理，只需要空间节点信息，不需要将节点连接成网格单元，与使用网格的传统算法相比，可以彻底或部分地脱离网格，适合于复杂外形流场的计算[4]。 发展无网格方法求解流动控制方程是解决传统数值模拟方法网格生成瓶颈问题的一种新尝试。

经过多年的发展，无网格方法已成功应用于材料动力学、结构动力学等领域，在航天器解体、空间碎片防护等领域展现出了很好的应用前景[6-10]。 Batina[11]首先将无网格方法应用于计算流体力学，发展了用于求解气体流动问题的无网格方法。 Oñate 和Ortega 等[12-14]先后将所发展的无网格数值方法成功用于求解对流扩散问题、不可 压 流 动、 可 压 缩 流 动、 势 流 等 问 题。 Katz等[15-16]将无网格方法用于重叠网格之间的信息交换，开展了无网格体积法(Meshless volume scheme)和多重点云(Multicloud)方法的研究。 此外，国外还有很多学者开展了与求解气体流动的无网格方法相关的通量格式、隐式方法、性能比较分析以及结合笛卡尔网格等方面的研究[17-20]。国内将无网格方法运用于计算流体力学的研究起步较晚。 陈红全等[21-22]和叶正寅等[23-24]较早开展了该领域研究。 近年来，陈红全研究团队和谭俊杰、许厚谦等研究团队开展了大量采用无网格方法数值求解气体流动问题的研究，包括无网格与笛卡尔网格混合算法[25-26]、无网格方法误差分析[27]、无网格方法求解非定常问题[28-30]等相关领域。

早期无网格方法研究中，求解无粘通量多采用添加人工耗散的中心差分格式。 该法具有形式简单、计算效率高等优势，但在耗散项中引入了经验参数，针对不同问题需要对参数进行人为调整，且很难推广应用到高超声速流动甚至非平衡流动的模拟。 由于对通量格式鲁棒性的要求更高，模拟非平衡流动时，传统网格法多采用矢通量分裂格式，其中Steger-Warming(SW)格式得到广泛应用[31-36]。 在求解气体流动的无网格方法研究中，尚未见采用SW 格式求解无粘通量的报道。

本文以无粘Euler 方程为研究对象，推导适于无网格方法的SW 通量格式，建立求解二维无粘气体流动的最小二乘无网格方法，并通过二维翼型、带斜面管道流动以及类解体碎片圆柱绕流干扰问题等典型算例对方法进行验证。 由于碰撞或寿命末期大型航天器解体后，会产生大量碎片，相互之间会产生干扰，进而影响其气动特性和飞行航迹。 本文以串列和并列双圆柱作为航天器多次解体残骸碎片简化模型，采用建立的无网格数值方法分析圆柱间距对碎片流场特性的影响。

2 无网格方法计算原理

无网格方法基本思想是基于空间离散点，在局部计算域内按一定法则构造一系列点云，求解区域用点云离散代替网格单元，点云由中间的中心点和周围的卫星点组成，在点云上通过特定方法构建空间导数的近似表达式，进而对流动控制方程求解，通过更新计算域内离散点处的流场信息，摆脱对离散网格的依赖，因此在求解诸如航天器解体残骸碎片等复杂非规则外形绕流时更具灵活性。 常见求解气体流动问题的无网格方法有基于泰勒展开的最小二乘法(TLS)、基于多项式展开的最小二乘法(PLS)和径向基函数(RBF)法等[4，6-12]，本文采用TLS 对流场进行模拟。

在二维局部域上构建点云结构，即确定中心点和卫星点，如图1 所示，假设i 为点云中心点，j为其卫星点(共m 个)。 为了降低点云结构中卫星点距中心点距离对空间导数求解精度的影响，需要引入权函数，且权函数应在数学上满足单调性、紧支性、正定性等条件[4]。

图1 点云结构Fig.1 Cloud of points

卫星点上的任意流场参数φ 按泰勒级数展开，可由中心点的参数近似表达，见式(1):

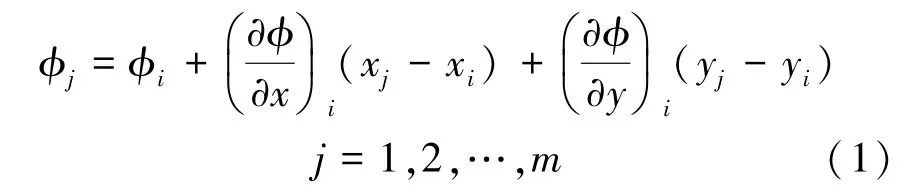
在中心点为i 的点云结构上建立如下总体误差函数，见式(2):

为了使式(2)的总体误差达到最小，采用最小二乘法可获得流场参数空间导数的表达式如式(4)所示:

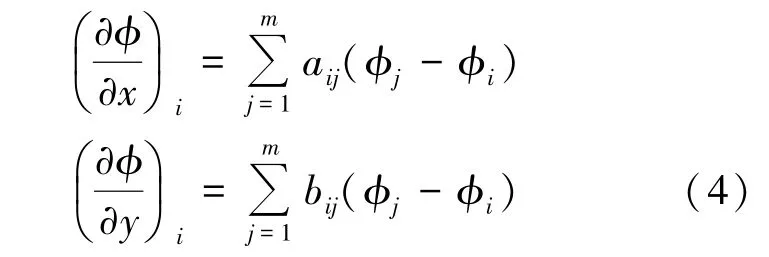
式中，最小二乘系数aij、bij只与点云结构中的离散点位置坐标有关，如果求解过程中点云结构不发生变化，则系数可以在迭代之前保存，无需参与迭代。

3 数值方法

3.1 流动控制方程

笛卡尔坐标系下的二维完全气体流动控制方程表达如式(5)所示:

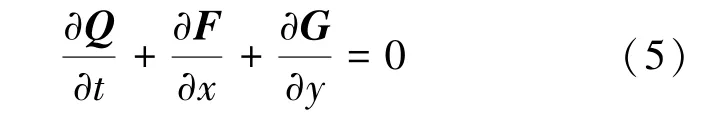
式中，Q 为守恒变量，t 为时间，F、G 分别为x、y 方向的无粘通量，如式(6)所示:

式中，ρ、p、E 分别表示气体密度、压力和单位质量总能，u、v 分别表示x、y 方向的速度分量。

3.2 空间离散

通过最小二乘法获得空间导数的基础上，空间点i 上的流动控制方程可写成式(7):

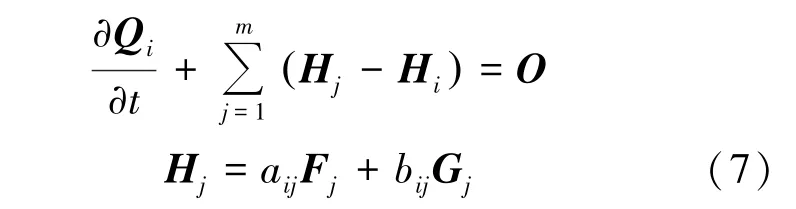
或式(8):

式中，下标j ＋1/2 代表点云的中心点i 到卫星点j 连线半点上的参数。 求解式(7)或(8)，即可得流场参数。 采用中心差分格式时，主要采用端点表达形式，而采用SW 格式等迎风格式时，则采用半点表达形式，方便重构以提高求解精度。

3.3 SW 通量格式

与传统网格法不同，式(7)或(8)中多出了在中心点的通量项Hi，该项直接采用中心点参数获得，而在中心点i 与卫星点j 连线的半点上，则和网格法一样需要对变量进行重构以提高求解精度，同时需要添加斜率限制器防止振荡[37]。

采用添加min mod 限制器的MUSCL 重构方法，无粘通量基于重构原始变量的SW 分裂表达式见式(9):

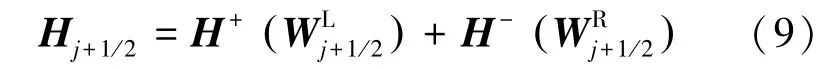
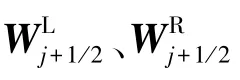
半点上原始变量重构差值见式(10):

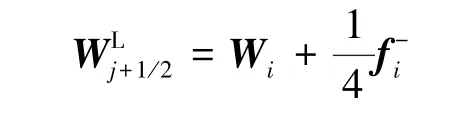
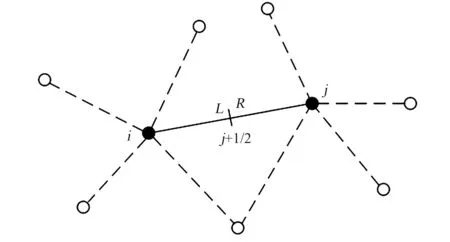
图2 半点重构示意图Fig.2 Reconstruction schematic at midpoint

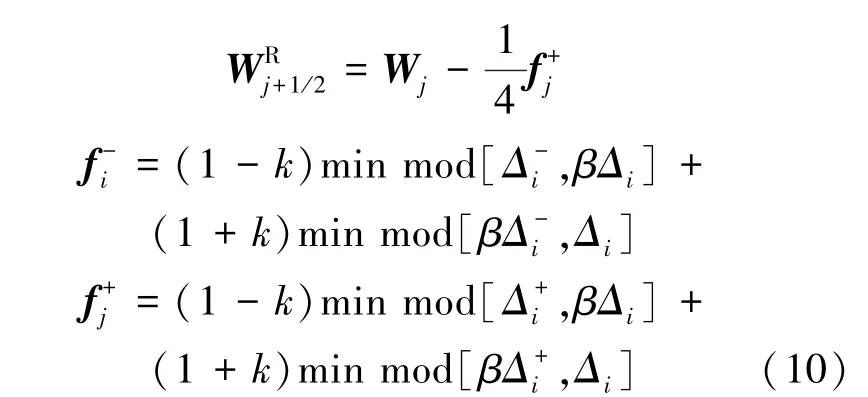
计算中参数k 和β 都取1.0，式中差分算子表示见式(11):

在重构变量的基础上，引入无网格最小二乘系数，推导得到半点上基于SW 格式的无粘通量分裂后的表达式为式(12)、(13):

式中，

式中，γ 为气体比热比，c 为气体声速，λ1、λ2、λ3为通量雅可比矩阵的3 个特征值，式(12)中正负特征值定义为式(14):

式中，ε 取一个极小的正数，以防止在声速点附近出现波动。

3.4 边界条件

采用无网格方法求解流动控制方程时，同样需要给出合适的定解条件，初始条件确定相对容易，而边界条件则相对复杂，处理不当会降低解的稳定性和准确性。 对外流而言，主要涉及固壁边界条件和远场边界条件的数值处理。

无粘流动要求固壁上流动满足无穿透条件，即在固壁上法向速度为0，压力、密度法向梯度均为0。 首先由边界点的点云结构中的内点卫星点通过镜像获得虚拟点坐标，将虚拟点加入边界点的点云结构中，通过法向梯度条件获得虚拟点上的参数值，再计算得到固壁边界点上的参数，参与流场求解[38]。

设置远场边界是为了减少有限的计算区域对模拟结果的影响，根据特征化基础边界条件确定，须保证向外传播的扰动波不会被边界反射到内场，处理方法和网格法类似。 若边界位置流动为超声速，则入口边界条件直接由上游参数赋值，所有出口边界条件均用外插获得；若流动为亚声速，则通过垂直于边界的Riemann 不变量获得边界点上的流动参数。

3.5 时间离散推进

由式(7)或(8)可得到i 点的Euler 方程半离散形式，如式(15)所示:

时间离散推进过程采用具有强稳定性的三阶SSP 型Runge-Kutta 法，由第n 时间步到第n ＋1时间步的迭代过程如式(16)所示:

在求解Euler 方程时，求解时间步长Δt 由格式稳定性条件决定。 在图1 所示点云结构中，点云半径较小的区域Δt 较小，而在点云半径较大的区域Δt 则较大。 对定常流计算，只要求得到最终的稳态解，时间步长取局部当地稳定性条件所允许的最大值，可大大加速整体计算推进过程，缩短计算时间[4]。 为此，在迭代过程中，采用局部时间步长和残值光顺加速收敛技术，提高数值计算的收敛速度[29，38]。

4 算法验证

4.1 NACA0012 翼型绕流

采用经典的NACA0012 翼型跨声速和超声速绕流流场算例对建立的最小二乘无网格数值方法进行验证。 计算域的远场边界距物面大约为20倍弦长，流场离散点基于结构网格生成，共有离散点20 307 个，其中固壁上有133 个，翼型表面附近区域空间离散点分布如图3 所示。 分别模拟来流马赫数0.8、迎角1.25°，以及来流马赫数1.2、迎角7°两个状态的跨声速和超声速流动。

图3 NACA0012 翼型壁面附近区域离散点Fig.3 Point distribution around NACA0012 airfoil

图4 中绘出了NACA0012 翼型跨声速M∞＝0.8，α ＝1.25°绕流流场压力分布云图，可以看出采用SW 格式的无网格方法很好地捕捉到了上下表面的激波。 为了更加清晰地比较分析不同方法结果特点与变化规律，图5 将本文无网格方法获得的该翼型表面压力系数与采用AUSM＋-up 格式计算得到的结果[24]以及实验测量数据[26](EXP)进行了比较。 可以看出，在激波附近区域，基于SW 无粘格式的无网格方法并未出现数值振荡或数值过冲，表明该格式具有很好的鲁棒性；其余区域压力系数也与实验测量值吻合很好，验证了所建立无网格方法模型的可靠性。

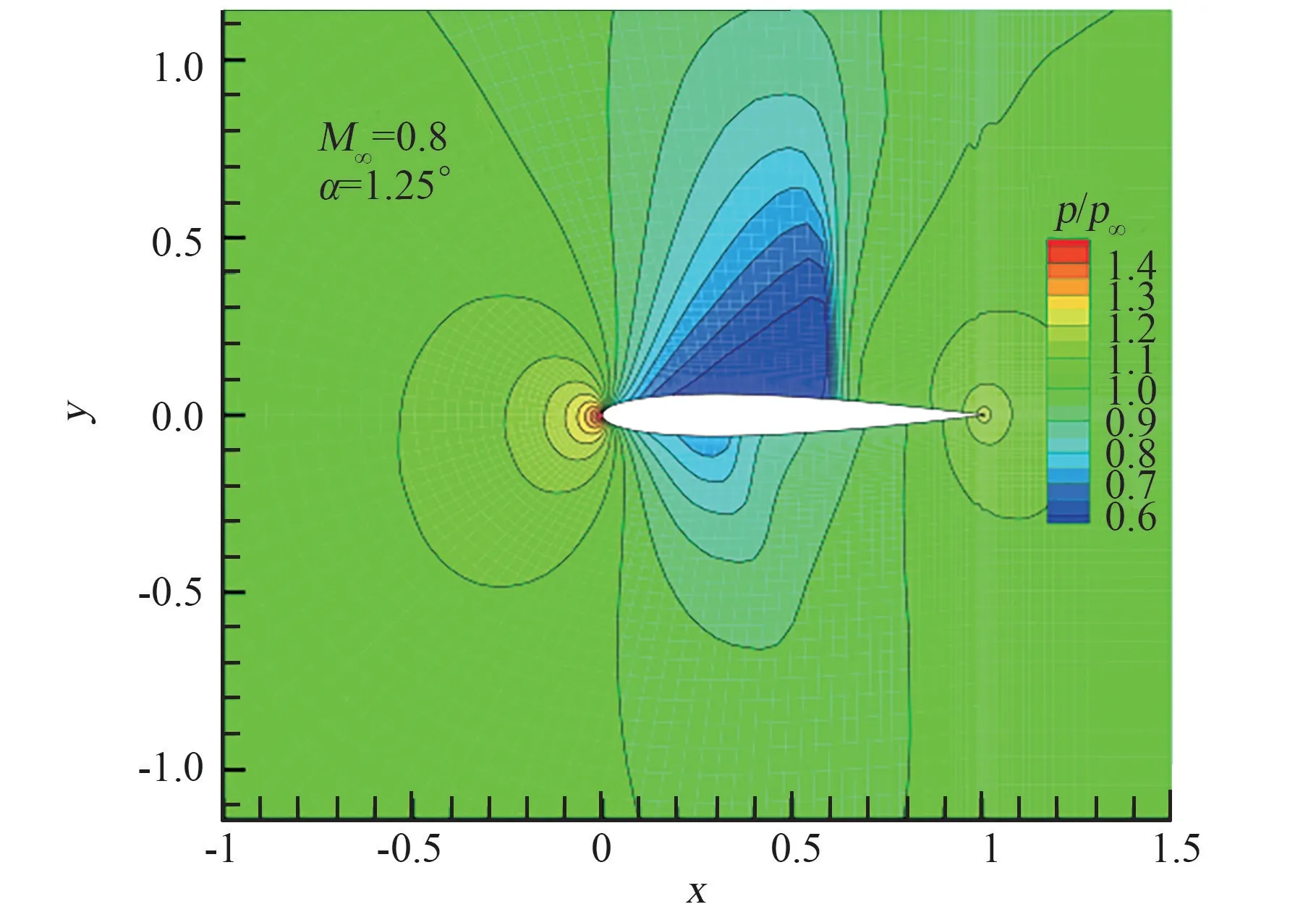
图4 NACA0012 翼型跨声速流场压力分布Fig.4 Pressure contours of NACA0012 transonic flow

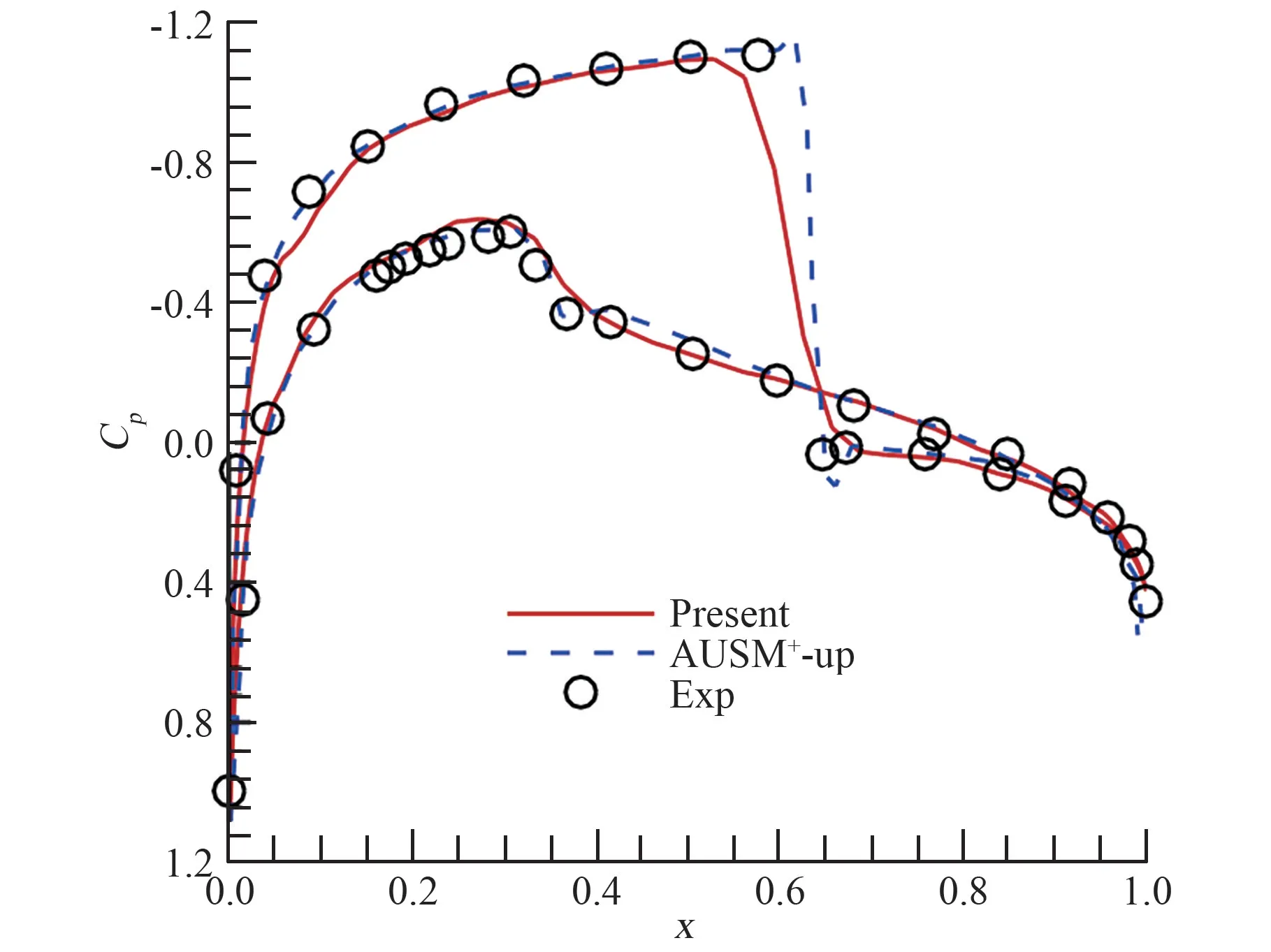
图5 NACA0012 翼型跨声速绕流壁面压力系数比较Fig.5 Comparison of surface pressure coefficient distribution in NACA0012 transonic flow

图6 和图7 分别绘出了NACA0012 翼型超声速M∞＝1.2、α＝7°绕流流场压力分布以及壁面压力系数的比较情况。 可以看出对超声速流动而言，采用SW 格式的无网格数值方法获得的翼型上下表面压力系数与采用其他如Roe 格式文献计算结果[29]以及实验测量值[26](EXP)吻合很好，表明发展的无网格方法模拟二维超声速流动的准确可靠性。

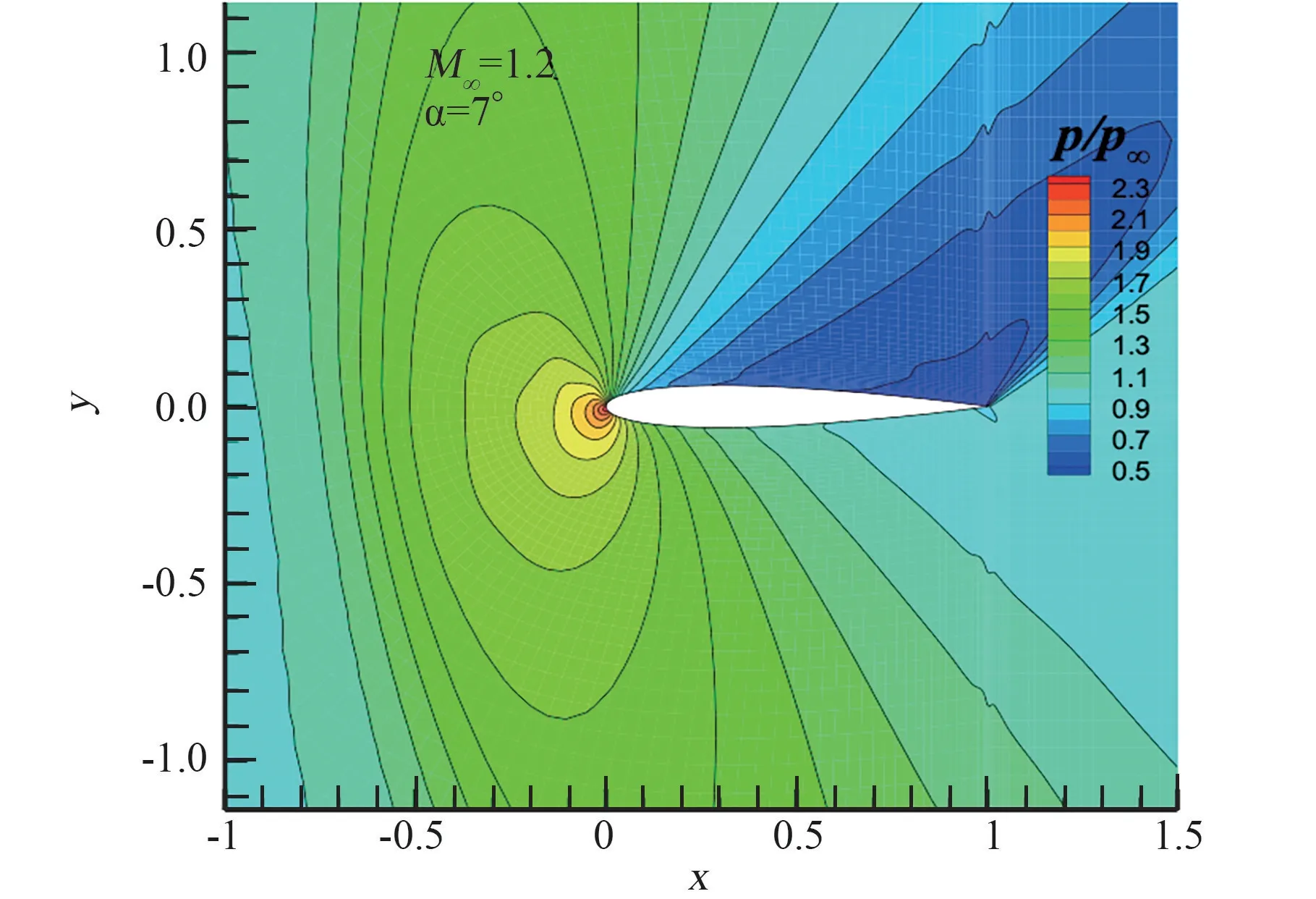
图6 NACA0012 翼型超声速流场压力分布Fig.6 Pressure contours of NACA 0012 supersonic flow

图7 NACA0012 翼型超声速绕流壁面压力系数比较Fig.7 Comparison of surface pressure coefficient distribution for NACA0012 supersonic flow

4.2 带斜面管道流动

采用建立的无网格数值方法模拟如图8 的超声速管道流动，入口马赫数2.0，流场离散点数目共5781 个，其中下壁面141 个。

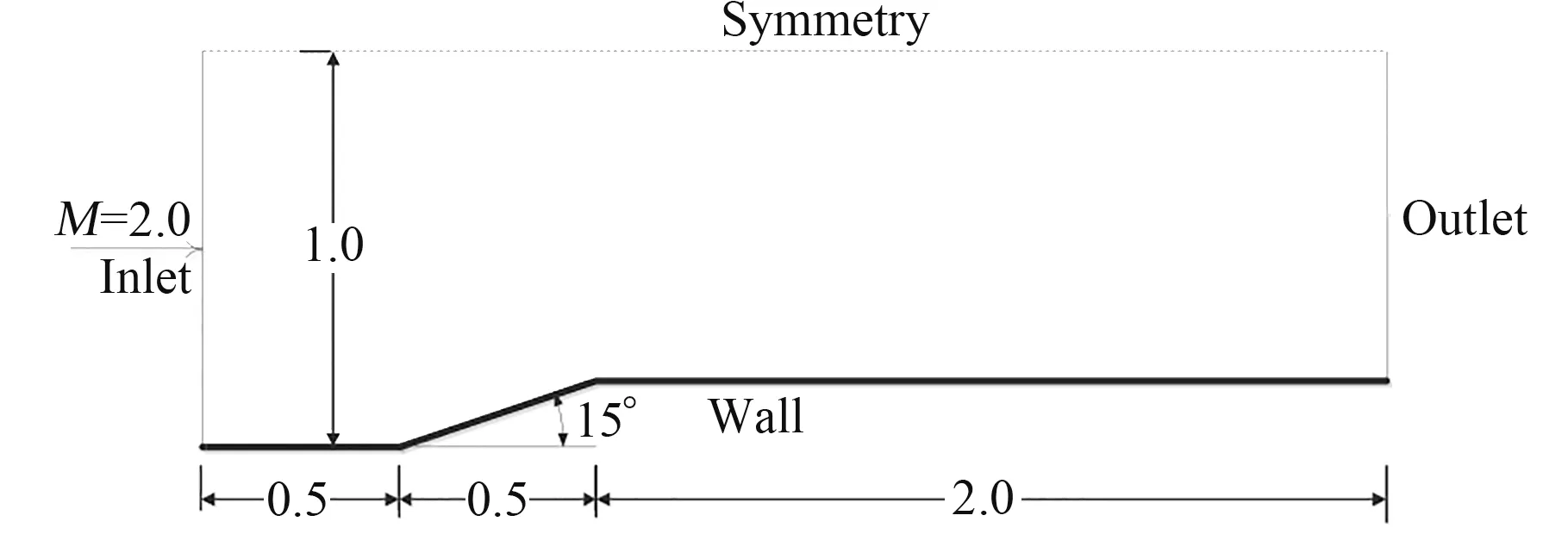
图8 管道流动结构图Fig.8 Configuration of the channel flow

通过数值模拟获得了管道流动流场中的压力、马赫数等参数分布，从图9 和图10 可以看出，流场参数分布合理，很好地描述了流场结构，包括对称面上激波相交与管道壁面上激波反射现象。

根据来流马赫数和尖劈角通过方程(17)可得激波角:

式中，δ 为尖劈角，β 为激波角，γ 为气体比热比，M 为来流马赫数。

图9 管道流动中的压力分布Fig.9 Pressure contours for the channel flow

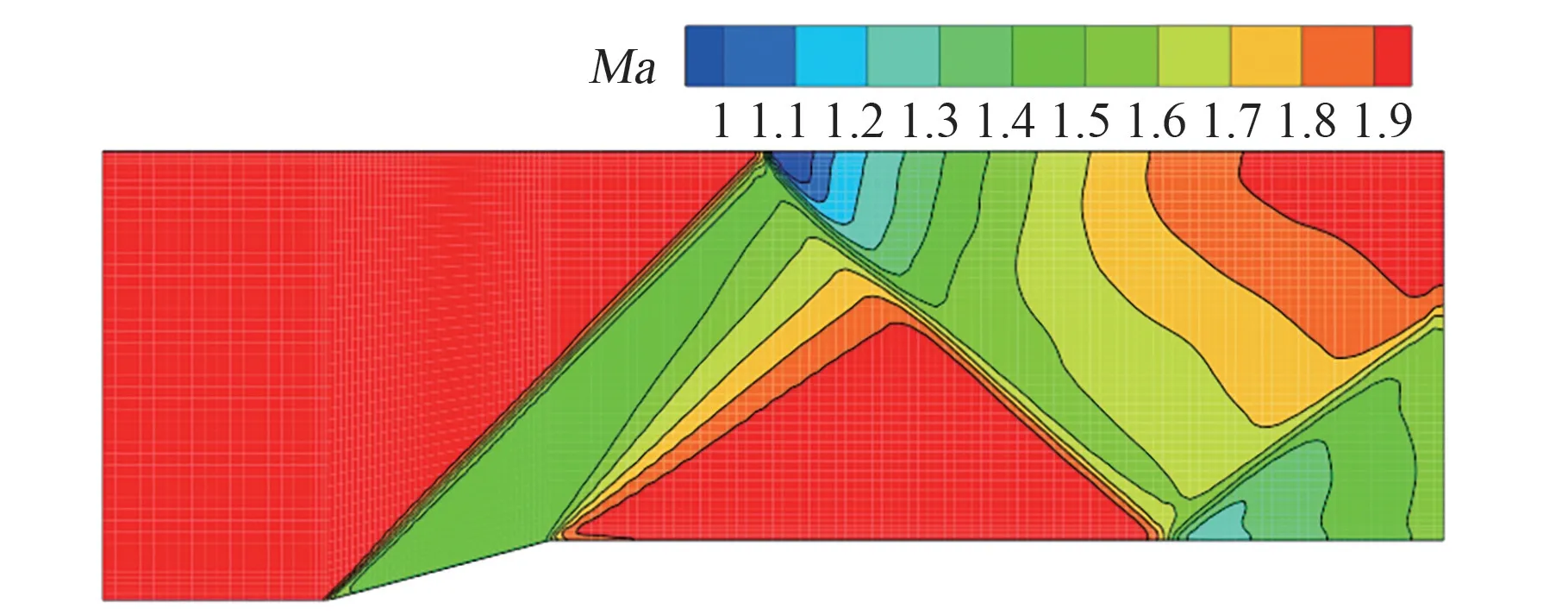
图10 管道流动中的马赫数分布Fig.10 Mach number contours for the channel flow

通过迭代可得该流动状态下管道内斜激波的激波角为45.344°，进而可以获得斜激波的准确位置。 图11 给出了下壁面和对称面上的马赫数分布，其中实心方块为下壁面上斜激波起始点和对称面上激波交叉点，可看出建立的无网格方法较好地捕捉了激波位置。

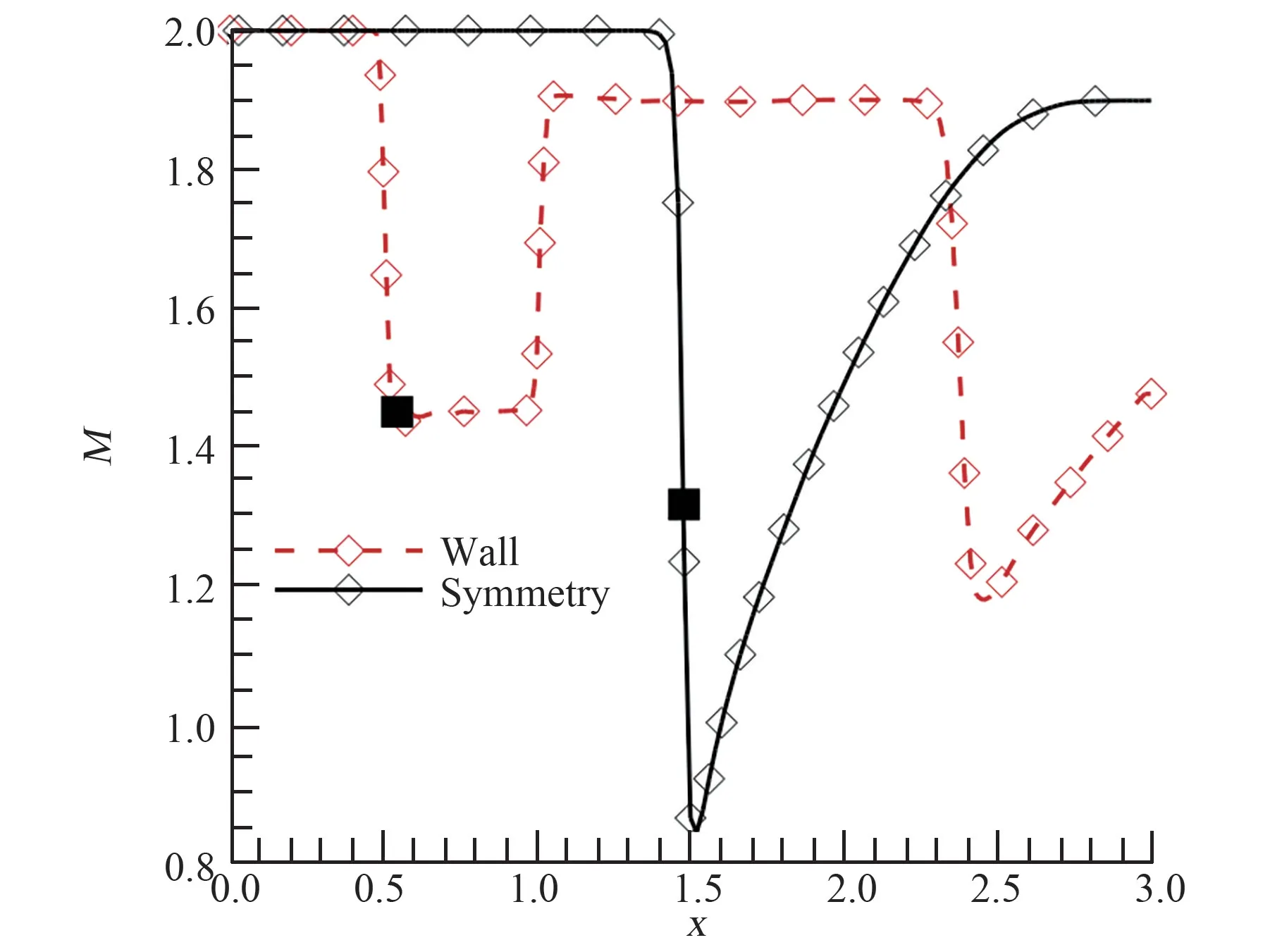
图11 管道流动边界上马赫数分布Fig.11 Mach number on boundaries of the channel flow

4.3 双圆柱绕流

为了描述近空间多次解体产生的残骸碎片间绕流干扰，拟定串列双圆柱绕流模拟两残骸碎片简化物绕流流动，在空间离散点或网格疏密分布相当和通量格式相同的基础上，与传统有限体积法进行对比验证，在比较时采用GLM 代表无网格方法，FVM 代表基于网格的有限体积法。

串列双圆柱圆心之间的距离为2 倍圆柱直径，模拟采用的流场空间离散点共有15 299 个，其中2 个圆柱壁面上共有128 个，圆柱附近空间离散点分布如图12 所示。 模拟状态为标准状况大气超声速流动，来流马赫数为1.5，迎角0°。

图12 串列双圆柱绕流流场离散点分布Fig.12 Point distribution around two cylinders in tandem arrangement

图13 比较了串列双圆柱绕流流场密度分布，可看出无网格法和有限体积法得到的流场中脱体激波、膨胀波及尾迹等形状都比较接近。 图14 比较了两圆柱表面压力分布，绝大部分区域2 种方法结果吻合很好，在后驻点附近区域，无网格方法获得的压力略高，可能的原因有待进一步分析。

图13 双圆柱绕流密度分布比较Fig.13 Comparison of density for the flow over double cylinders

图14 圆柱表面的压力分布比较Fig.14 Comparison of surface pressure distribution of cylinders

5 解体碎片流场模拟

以串列双圆柱和并列双圆柱作为简化的航天器多次解体产生残骸碎片模型，采用建立的无网格方法对其绕流干扰流场进行模拟，分析碎片间距对流场特性的影响。 假设圆柱直径为D，设置串列双圆柱间距分别为2D、4D、8D，模拟高度30 km，飞行速度900 m/s，对并列双圆柱间距分别为3D、6D、12D，模拟高度50 km，飞行速度800 m/s。

图15 给出了不同间距的串列双圆柱绕流流场压力分布比较情况。 可以看出，当一块碎片处于另一块碎片之后时，由于前面碎片尾流的影响，后面碎片来流速度明显降低，驻点压力也会低于前面碎片，当间距很小时甚至在后面碎片的头部区域都不能形成超声速流场。 这种情况下，后面碎片的升力更小，所以下降比前面碎片要快。 图16 比较了不同间距的并列双圆柱绕流流场压力分布。 对并列的2 块碎片，间距很小的时候存在相互干扰，由于中间压力增大，碎片运动会朝着增大间距的方向发展，随着间距的增大，干扰逐渐降低直至消失。 就模拟状态而言，当并列圆柱之间的间距大于6 倍圆柱直径时，二者之间几乎不再相互干扰。 研究结果说明碎片间距不同，相互之间流场干扰程度不同，进而对气动特性和飞行航迹的影响程度也不同。

图15 串列双圆柱绕流压力分布比较Fig.15 Comparison of pressure distribution for the flow over two tandem cylinders

图16 并列双圆柱绕流压力分布比较Fig.16 Comparison of pressure distribution for the flow over two side-by-side cylinders

6 结论

以求解无粘流Euler 方程为目标，推导建立了求解二维无粘流动的最小二乘无网格数值方法。 对典型算例和简化碎片模型绕流进行了求解，结论如下:

1) 针对典型翼型绕流、超声速管道流动和串列双圆柱绕流等问题，开展无网格数值方法模拟验证，得到了与实验数据、分析解以及文献和网格方法计算结果间的定量化比较确认。 分析表明构造设计的无网格方法无粘通量格式能够有效避免数值振荡和数值过冲，对精细捕捉基于Euler 方程描述的流场流动特征具有很好的收敛适应性与可靠性。

2) 以串列双圆柱和并列双圆柱作为简化模型开展航天器解体碎片超声速流场数值模拟，获得了不同排列方式和不同间距碎片的绕流流场，结果表明碎片间距增大，相互间的干扰减弱。 同时说明建立的无网格方法具备推广至开展近空间非规则物形粘性流动模拟的潜在能力，证实了算法模型的有效性。

3) 本文工作属初步阶段性，文中算例基于无粘假设，与真实流动还存在一定差异，更精细计算分析需要开展三维粘性流动无网格模拟方法。 下一步将围绕提高无网格方法数值精度与鲁棒性，开展无网格粘性流动模拟及无网格自适应方法研究，发展完善适于非规则物形绕流的无网格数值方法，并拓展应用于航天器多次解体残骸碎片气动力/热绕流问题模拟研究。