悬臂梁基底对压电俘能器输出响应的影响分析
2020-10-28吴新哲闫守阳高志强焦国太
吴新哲,闫守阳,高志强,韩 晶,焦国太
(中北大学 机电工程学院,山西 太原 030051)
0 引言
随着无线传感网络的不断发展,利用压电俘能器将周围自然环境中的风能[1-3]、振动等[4-5]机械能转化为电能,实现传感网络节点的自供电,已成为当前研究关注的热点。在各种类型的压电俘能器中,基于悬臂梁谐振形式的能量收集技术因结构简单、能量密度高等优点而被广泛应用。近年来,国内外学者针对形状尺寸[6-7]、中性面位置[8]、结构刚度[9]等方面进行了广泛研究,为压电俘能器的设计与应用奠定了理论基础。但目前利用悬臂梁结构的压电俘能器还存在能量输出小、谐振带宽低等技术问题尚未完全解决。事实上,在低风速环境条件下,研究压电悬臂梁的振动特性是提高压电俘能器性能的关键。为此,针对在1.5 ~5.8 m/s风速环境下,接触式压电俘能器对聚氯乙烯(PVC)、304不锈钢、1060铝和H68黄铜4种不同材料基底进行了对比实验,分别从自由振动、输出功率和能量转化率评估其响应特性,对风能压电俘能器的工程应用提供了一定的参考。
1 接触式压电俘能器
1.1 结构组成
接触式压电俘能器的结构组成如图1所示。工作时,风能驱动压电俘能器顶部的三杯式旋转机构实现旋转运动,进而通过拨片的冲击碰撞在悬臂梁上产生周期性激振力,带动悬臂梁进行自由振动。在此期间,机械能可通过压电薄膜聚偏氟乙烯(PVDF)转换为电能,并经全桥整流与充电电容,实现对于风能的能量俘获。同时,该结构中激振力的大小与拨片和悬臂梁之间的轴向方向上预先设定的重叠距离有关,该长度对悬臂梁的振幅、接触持续时间和压电风能发电装置的启动风速影响较大。

图1 接触式压电俘能器示意图
1.2 响应模型
图2为接触式压电俘能器模型。根据Euler-Bernoulli方程,夹紧-自由边界条件下,接触式压电俘能器的受迫振动方程为
(1)
式中:Ca和Cs分别为空气粘弹性阻尼和应变速率阻尼;E为弹性模量;Ib为压电悬臂梁的截面惯性矩;m为单位长度的质量;υ为耦合系数;yrel(x,t)为夹持端的相对振动位移;ybase(x,t)为夹持端的绝对振动位移。y(x,t)为压电悬臂梁相对于夹持端的振动位移,即
y(x,t)=ybase(x,t)+yrel(x,t)
(2)
ybase(x,t)=g(t)+xh(t)
(3)
式中:g(t)为外界拨片垂直激励;h(t)为夹持端微小旋转运动激励。

图2 接触式压电俘能器模型
模型中,假设拨片的接触面绝对光滑,与压电悬臂梁的接触长度是恒定的。由于重叠长度很小,忽略了表面滑动或承载牵引时可能产生的拉应力和切向力,且只有垂直的压力。赫兹线接触理论可用于确定每个拨出周期的弹性趋近量,则有
(4)

假设在第一个拨片周期中,在拨片接近悬臂尖端前,悬臂处于静止状态,故不需要考虑初始位置。在这种情况下,压电悬臂梁的整体位移实际是其相对位移,拨片与梁的平面之间的线接触,Fn可近似为线性比例:
Fn=kh×δn
(5)
式中kh为线性接触刚度,可以从式(4)中得到线性近似。
对于整个拨动状态,Fn可近似为
Fn=kh×yrel(x,t)
(6)
当不考虑微小旋转运动时,即h(t)=0,此时,输出电压简化为
(7)

2 实验搭建
接触式压电俘能器的实验装置如图3(a)所示。由于压电陶瓷(PZT)梁刚度较大,拨动悬臂梁所需风速较大,故选用柔性PVDF材料。使用的单晶型悬臂梁分别由80 mm×22 mm×0.28 mm的PVC、304不锈钢、H68黄铜和1060铝基底层和45 mm×20 mm×28 μm的PVDF压电薄膜组成(见图3(c))。为了方便更换不同基底的悬臂梁,悬臂梁结构单独安装在夹具上。拨片采用ABS材料,并且与悬臂梁的重叠长度为3 mm。当三杯式旋转机构在风能作用下开始旋转后,悬臂梁将进行受迫振动,产生的输出电压经过MB6F整流桥进行整流后对负载提供电能。由于风速变化会改变整个系统的激振力频率,因此,在整个实验中选择了一组特定的风速值,使用调速器在1.5~5.8 m/s内调节实验的风速。表1为不同基底悬臂梁的参数。压电悬臂梁的共振频带窄,在实际环境中常处于非共振状态。针对1.5~5.8 m/s的实验环境,最大激励频率为7 Hz时对悬臂梁进行分析。通过实验得到了由PVC、304不锈钢、H68黄铜和1060铝为基底的压电悬臂梁的一阶固有频率分别为17.69 Hz、18.54 Hz、23.73 Hz和30.01 Hz。

表1 为不同基底悬臂梁的参数
3 结果与讨论
3.1 输出响应
图4是风速为3.8 m/s时,不同基底悬臂梁冲击振动条件下PVDF压电薄膜的输出响应曲线。由图可以看出,不同基底材料的冲击振动响应特性不同。其中,铝基底悬臂梁输出峰值电压最大可达3.07 V,铜和不锈钢基底的悬臂梁的输出电压分别为2.49 V和2.29 V,PVC基底的悬臂梁输出电压仅1 V。且在自由振动阶段其振动周期也不同,PVC基底悬臂梁振动周期可达0.059 s,不锈钢和铜基底悬臂梁振动周期分别为0.054 s和0.042 s,铝基底的悬臂梁振动周期仅0.033 s。

图4 不同基底压电悬臂梁的响应
3.2 输出功率
为了研究对比不同基底悬臂梁在不同风速下的输出功率,首先进行了阻抗匹配。图5是风速为3.8 m/s,不同基底压电悬臂梁负载电阻与输出功率的关系。由图可知,PVC和铝为基底压电悬臂梁最大功率分别可达0.149 μW和0.313 μW,而铜和不锈钢基底压电悬臂梁的最大功率分别达到0.465 μW和1.575 μW后,随着电阻的增加,功率衰减速度快。由此可看出,不锈钢基底悬臂梁功率最大,其次铜基底悬臂梁的输出功率,PVC基底悬臂梁的输出功率最小。同样条件下,不锈钢基底悬臂梁输出的最大功率是PVC基底悬臂梁输出的最大功率的10.6倍。

图5 不同基底的压电悬臂梁的输出功率
3.3 能量转化效率
为了更好地了解不同基底悬臂梁在低风速环境下的能量输出特性,有必要对能量转化率进行比较。在相同风速条件下,不同基底悬臂梁所受拨片给予的能量不同,悬臂梁输出的能量也不同。在一定时间内输入能量和输出能量分别为
(8)
(9)
式中:ma为拨片的质量;v1,v2分别为拨片与悬臂梁碰撞前、后的速度;Wh是在一定时间T内,电阻取值1时,对u2的积分;u为悬臂梁的输出电压。
在一定旋转风速下悬臂梁的能量收集效率定义为
(10)
根据式(10)可得到风速在3.8 m/s时悬臂梁的能量转化效率。其中,铜基底压电悬臂梁的能量转化效率最高为38.1%,铝和不锈钢基底压电悬臂梁的能量转化效率分别为32.1%,和29.7%。PVC基底压电悬臂梁的能量转化效率仅为3.6%。
3.4 基底结构参数的影响
3.4.1 结构刚度
风速值是系统的输入参数,在保持风速不变的情况下,系统的激振力频率保持不变。因此,拨片和悬臂梁之间的接触是周期性的。一旦设置了不同的风速,悬臂梁的输出电压就会显示出不同的轨迹。随着风速的增大,拨片的旋转频率增大,悬臂梁自由振动的时间缩短。图6为不同基底的压电悬臂梁在启动风速1.5 m/s、1.8 m/s、2.0 m/s和2.8 m/s下的输出电压曲线。由图可知,在启动风速下,不同基底悬臂梁旋转频率对悬臂梁自由振动时间的影响很小时,电压曲线在每个弹拨周期中呈现出近似完整的自由振动衰减脉冲形式,在拨片拨动梁后,输出电压立即上升到峰值,然后以自由振动形式衰减,直到下一次拨片激励。

图6 不同基底压电悬臂梁在启动风速下的响应
随着风速的增加,两个连续拨动周期间的时间间隔可能不足以使梁振动完全衰减,在这种情况下,悬臂梁仍在经历自由振动,电压曲线在每个弹拨周期中只呈现出部分自由振动衰减脉冲。图7为4.8 m/s风速下不同基底悬臂梁的实验输出电压曲线。

图7 不同基底压电悬臂梁的实验输出电压曲线
PVC基底压电悬臂梁在风速为1.5 m/s时,拨片可拨动悬臂梁进行转动,在风速为4.8 m/s时,激励频率可达5.41 Hz,不但启动风速低,且激振力频率快。而不锈钢和铝基底压电悬臂梁分别需在风速为1.8 m/s和2 m/s时,拨片才可拨动压电悬臂梁进行旋转,在风速为4.8 m/s时,激振力频率分别为5.05 Hz和4.55 Hz,启动风速较低,激振力频率较快。铜基底压电悬臂梁在风速为2.7 m/s时,拨片才可拨动悬臂梁进行旋转,在风速为4.8 m/s时,激振力频率仅有4.23 Hz,启动风速高,激振力频率慢。通过实验可以发现,PVC、304不锈钢、1060铝和H68黄铜基底悬臂梁的结构刚度(K)分别为16.55 N/m、54.27 N/m、98.78 N/m和185.85 N/m。由此可发现,悬臂梁的K对系统的启动风速和激振力频率影响较大。由于K的不同,在相同风速条件下所受激振力频率也不同。随着K的增加,压电悬臂梁所需启动风速越来越高,且在相同风速条件下,随着K的增加,激振力频率越来越小。
3.4.2 减幅因数
图8为风速1.5~5.8 m/s、不同风速下不同基底的压电悬臂梁的最大输出功率。由图可知,在整个风速范围内,所有压电悬臂梁的输出功率随着风速的增加而增加。其中不锈钢基底的压电悬臂梁输出功率在不同风速下始终最高,在5.8 m/s的风速下,输出功率可达到5.59 μW,同等条件下,不锈钢基底的压电悬臂梁输出功率分别是PVC、铝和铜基底的压电悬臂梁输出功率的15.3,13.1和8.0倍。其中PVC基底的压电悬臂梁输出功率最小,仅为0.365 μW。
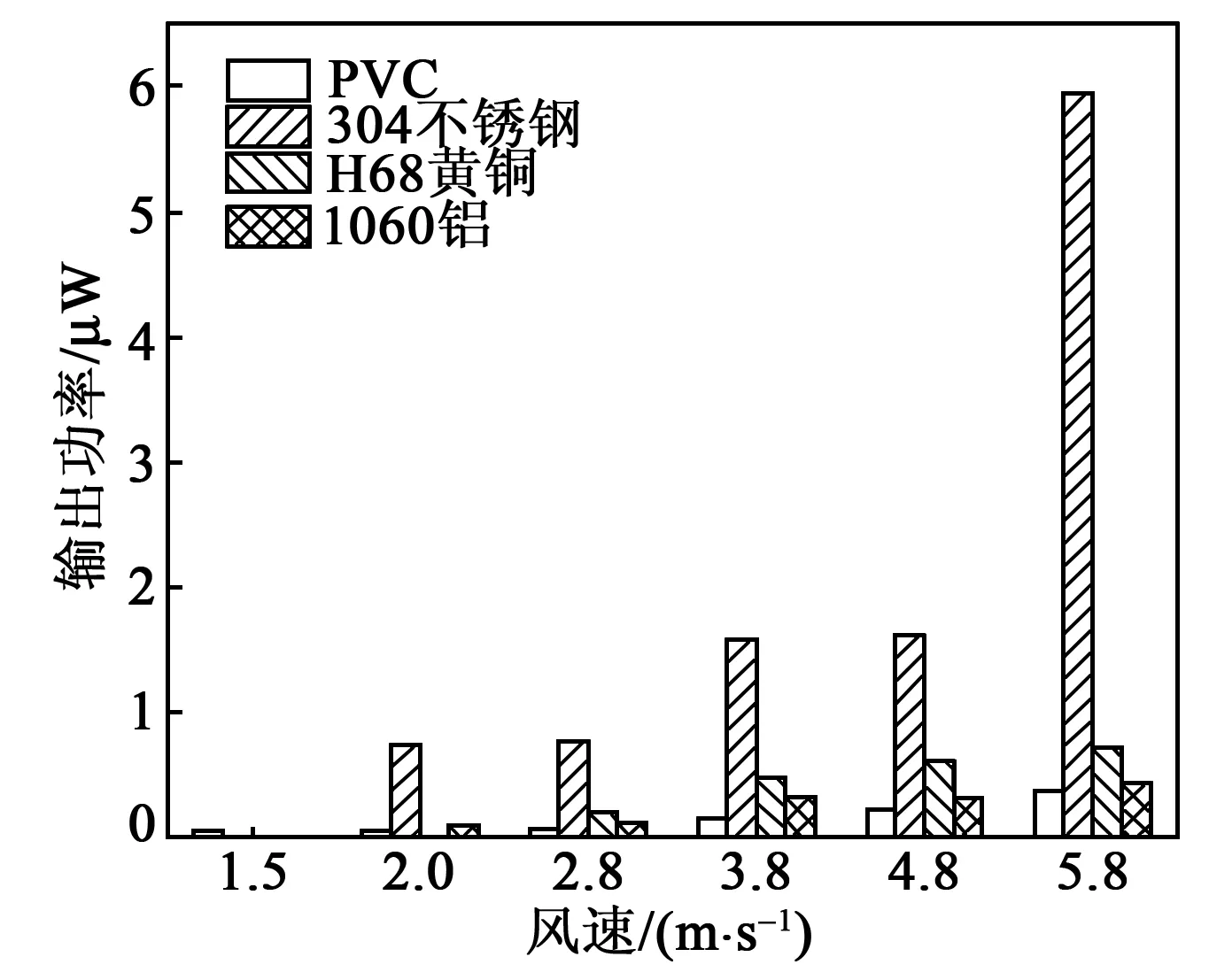
图8 不同风速下不同材料基底的悬臂梁最大输出功率
由图6、7可知,不同基底的悬臂梁处于欠阻尼振动状态,且不同压电悬臂梁的输出电压衰减速度不同,所以有必要对悬臂梁的减幅因数(η)进行分析。设衰减振动时,同侧任意相邻的两个振幅分别为Ai和Ai+1,则:
(11)
式中:δ为阻尼系数;T1为衰减振动的周期,欠阻尼状态下T1≈T2,T2为梁的固有周期。
经过一个周期,振幅衰减到原有的e-δT1倍。通过实验得出,以PVC、铝、铜和不锈钢为基底的压电悬臂梁系统的η分别为1.9、1.49、1.47和1.25。每振动一次,PVC基底、铜基底及不锈钢基底的压电悬臂梁系统的电压振幅分别减小了 47.3%,32.9%,32.0%,20.0%。由此可知,η越小,压电悬臂梁系统的电压振幅衰减越小。由图8可知,η越小,悬臂梁的输出功率越大。这表明,η影响了压电悬臂梁的输出电压的振幅衰减速度,进而影响压电悬臂梁的输出功率。
在2.8~5.8 m/s低风速下,以PVC、不锈钢、铜和铝为基底悬臂梁的能量转化效率随着风速的增加而减小,如图9所示。由图可知,在2.8~3.8 m/s风速下,铜基底压电悬臂梁能量转化率最高,分别达到42.6%和38.1%;而在4.8~5.8 m/s风速下,铝基底压电悬臂梁能量转化率最高,分别为24.3%和14%。在整个低风速环境下,PVC基底悬臂梁能量转化率最低。
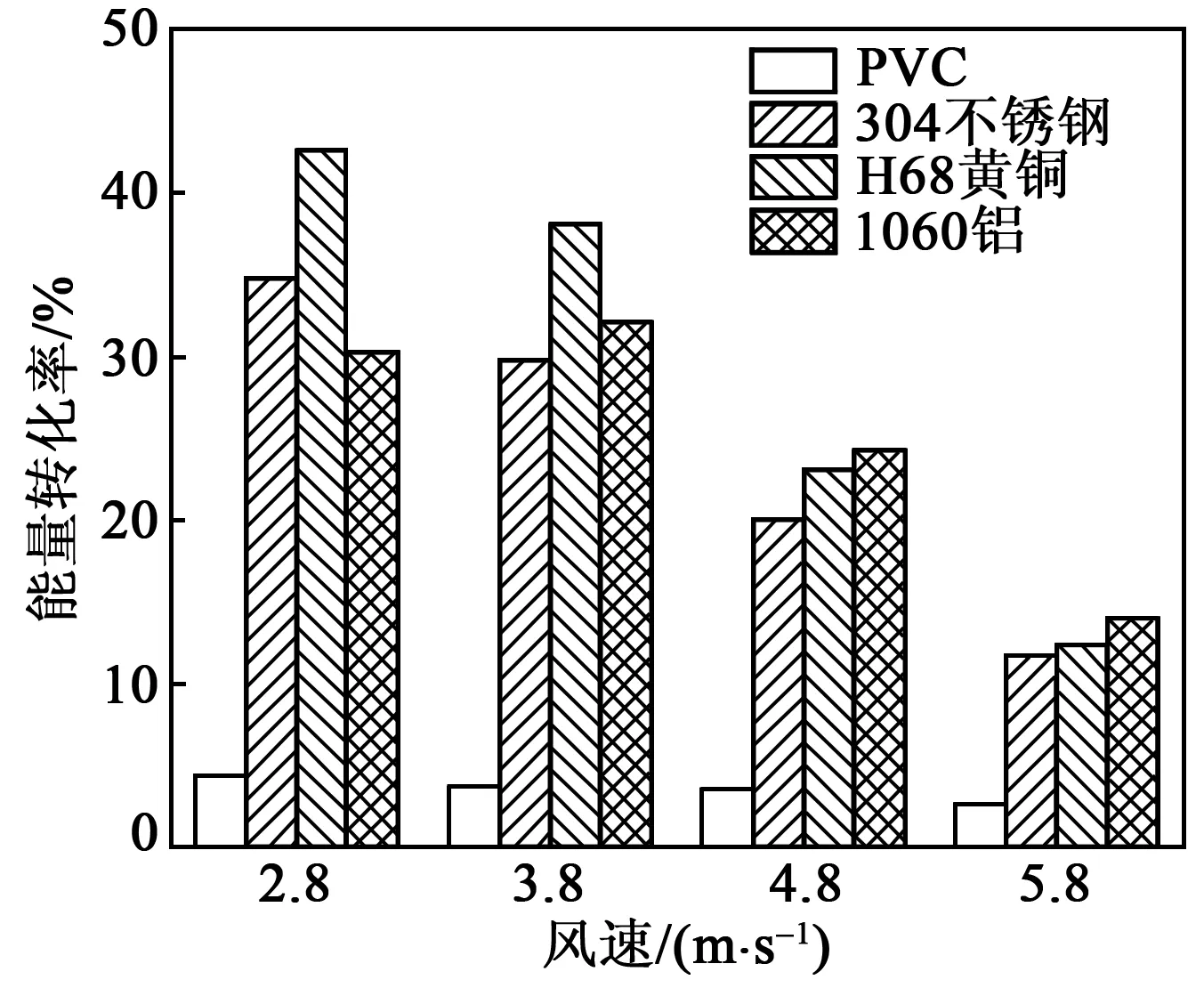
图9 不同风速下悬臂梁的能量转化效率图
在2.8~3.8 m/s风速下,铜基底压电悬臂梁的输出电压峰值比铝基底压电悬臂梁的输出电压峰值小,但减幅因数小,结构刚度大,受到的激振力频率慢,在2个连续拨动周期间有较长的时间把振动能转化为电能。此时,铜基底悬臂梁能量转化效率比铝基底的转化效率高。在4.8~5.8 m/s风速下,随着激振力频率的增加,在2个连续拨动周期间,无足够的时间将振动能转化为电能,输出电压在还未衰减到峰值电压一半时,就会受到拨片的第二次拨动,悬臂梁的输出峰值电压成为影响能量转化率的首要因素。此时,铝基底悬臂梁的转化效率比铜基底悬臂梁的转化效率高。
整个低风速范围内,以PVC、铝、铜和不锈钢为基底的悬臂梁随着风速增加,自由振动时间缩短,本应转化为电能的振动能在与拨片的碰撞中损耗,这是导致能量转化效率随着风速的增加而减小的重要因素。
4 结论
合适的基底材料能够更好地提高悬臂梁式压电风能发电装置的输出特性。该文基于接触式压电俘能器,在1.5~5.8 m/s低风速下,对PVC、304不锈钢、1060铝和H68黄铜基底的PVDF式压电悬臂梁进行了实验对比,得出以下结论:
1) 在整个低风速范围内,304不锈钢基底的输出功率最大,可达到5.59 μW,同等条件下,分别是PVC、铝和铜基底的压电悬臂梁输出功率的15.3,13.1和8.0倍。
2) 在2.8~3.8 m/s风速下,H68黄铜基底压电悬臂梁能量转化率最高。在4.8~5.8 m/s风速下,1060铝基底的压电悬臂梁能量转化率最高。
3) 对悬臂梁的参数进行分析发现,悬臂梁的结构刚度越小,系统的激振力频率越大,启动风速越低。减幅因数越小,悬臂梁的输出功率越大。
