TWUSM振动模态鲁棒滑模观测器研究

荆 锴，林夏萍，董 砚

(1.河北工业大学 人工智能与数据科学学院，天津 300401；2. 河北省控制工程技术研究中心，天津 300130)

0 引言

行波型旋转超声电机(TWUSM)是利用定子上压电陶瓷片的逆压电效应，施加高频电压激励时产生高频振动，引起定子表面质点的椭圆运动。由于定、转子受到预压力作用相互接触，定子表面质点的椭圆运动将对转子产生摩擦力，驱动转子旋转运动，该过程通过定子微观运动实现能量转换，伴随严重非线性特征，且定子状态难以观察。

早期TWUSM控制技术的发展主要集中在基于系统级输出量(如转子转速、转矩)进行控制器设计研究[1-3]，但从电机驱动机理可知，两相振动模态是产生行波、驱动电机运行的关键，直接影响电机控制性能，然而以定子振动模态进行电机优化、控制还较少。已有研究利用变压器电桥电路[4]、形变检测传感器[5]、高速摄像头[6]等测量振动特性，用来分析电机状态及提供控制补偿。但这些装置复杂且不易安装，利用观测器对状态量进行获取则是更好的选择，早期研究中提出，根据定子等效电路模型构建两相振动模态观测器方法的进行观测[7]，但未做深入研究。

针对超声电机具有强非线性、参数不稳定等特征，本文提出了一种利用具有强鲁棒性、强抗扰性的滑模观测器[8]的振动模态观测器设计方法，并基于此通过振动模态的优化，改善电机的运行性能。

1 TWUSM运行机理分析

TWUSM在两相等频等幅相位差为π/2的正弦激励电压u=[uAuB]T下定子产生两相振动模态w=[wAwB]T，且满足机电耦合方程及压电振子方程：

(1)

(2)

式中：m，d，c，Θ分别为定子两相的模态质量、模态阻尼、模态刚度及机电耦合系数；fc为定转子相互作用产生的模态力；Rd，Cd分别为两相压电振子的介电损耗电阻和静态电容；i= [iAiB]T为相电流。

激励作用下定子产生两相振动模态，并在定子中合成一列行波，只有当wA和wB等幅正交时，合成理想型波，即

w=wAsin(kθ)+wBcos(kθ)=

Wsinωtsin(kθ)+Wcos(ωt)cos(kθ)=

Wcos(kθ-ωt)

(3)

式中W为A、B两相振动模态的幅值。由于制作工艺、环境影响等无法获得理想的对称定子，导致定子中激发的两相振动模态并不严格等幅正交，使得合成行波中夹杂一定的驻波，进而带来转矩脉动及多余的损耗，降低了电机精密驱动性能。

两相振动模态对于电机高精度控制具有重要意义，但振动模态不易测量，下面将设计鲁棒滑模观测器对其进行估计。

2 振动模态滑模观测器设计

2.1 TWUSM振动模态状态方程

(4)

考虑超声电机参数测量误差及易受环境影响而改变，参数c,d,m存在的不确定性影响电机运转，实际的系数矩阵可写成：

(5)

系统的不确定性产生的影响与模态力是同维度的，可合并为一项(h(t,x,u))，并一定有界 |h(t,x,u)| ≤D，且有：

h(t,x,u)=Δb2u+ΔA21x1+ΔA22x2+

(6)

另表示状态方程为

(7)

系统存在不确定性项，设计滑模观测器需要考虑其影响，并做出恰当设计以克服系统不确定性。

2.2 滑模观测器设计

滑模观测器利用观测输出与实际输出偏差的开关函数形式返回输入端，使输出偏差快速逼近0，从而达到观测系统快速逼近实际系统的目的，获得准确的观测值。

针对上述系统，设计如下观测器：

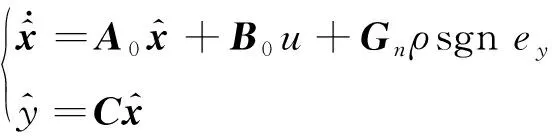
(8)

式中Gn=[L-1]TL为用户设计量。

(9)

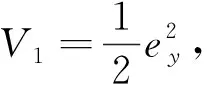
-|ey|(ρ-|A21e1+A22ey+h(t,x,u)|)≤ -|ey|(ρ-|A21e1+A22ey+D|)

(10)

当ρ>|A21e1+A22ey+D|时，系统可到达滑模面。到达滑模面后，ey=0：

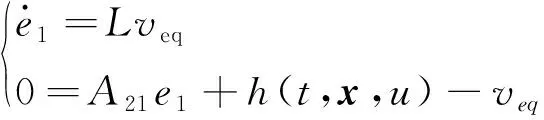
(11)

简化式(11)为

(12)

利用观测得到的电机两相振动模态来调节电机两相输入电压的幅值和相位，从而改善两相振动模态，使其等幅正交，进而优化电机输出转矩的性能，减小脉动，降低损耗。

3 仿真与实验

图1 TWUSM基于滑模观测器的控制框图

3.1 滑模观测器性能仿真分析

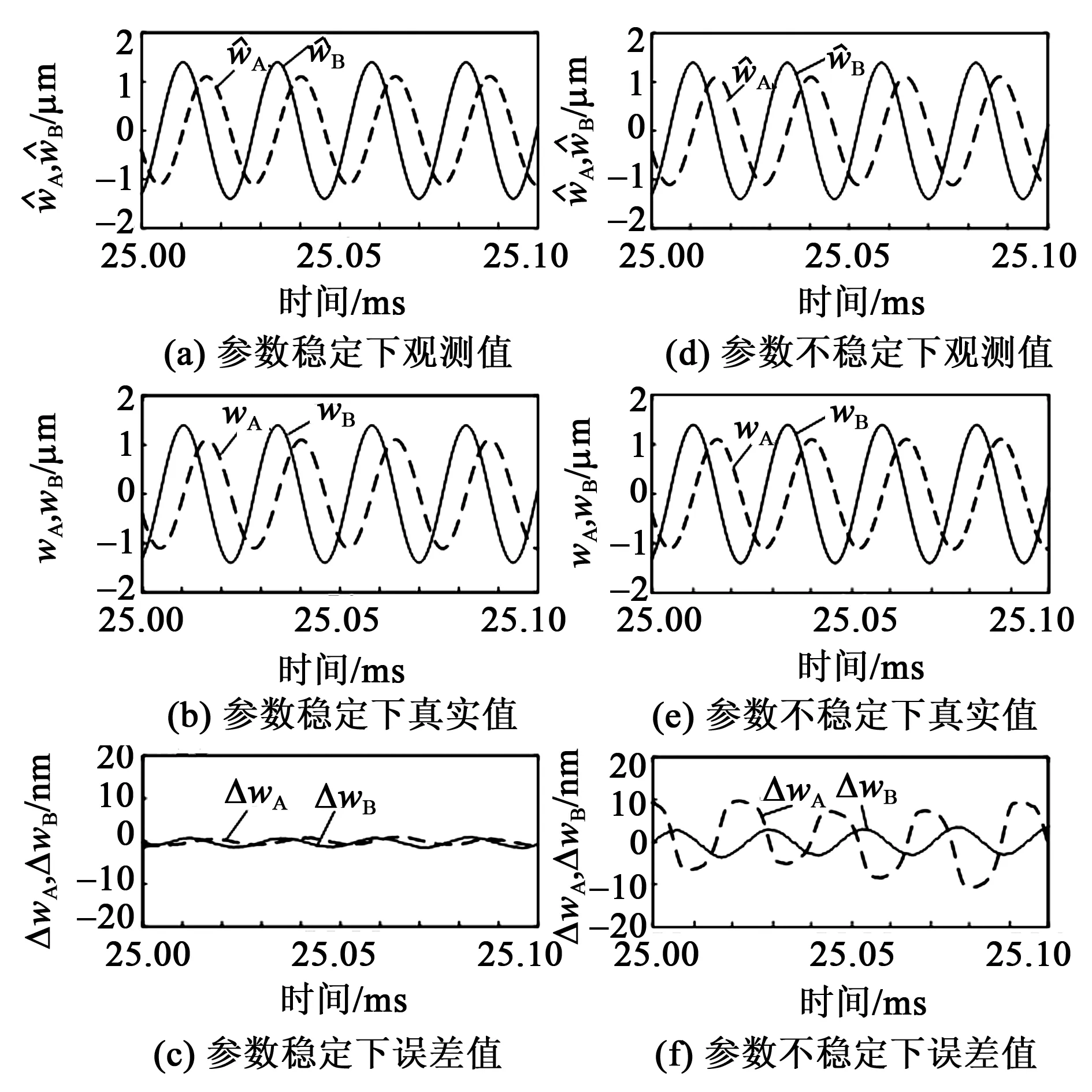
图2 稳态下两相振动模态曲线、观测曲线及误差曲线

根据所观测的振动模态，调节全桥驱动电路两相方波电压的占空比，实现振动模态的等幅正交。图3(a)、(b)和(d)、(e)分别为调节前、后相电压、振动模态曲线。由图可看出，调节前，A、B两相模态幅值分别为1.111 μm和1.408 μm，且相位接近π/2；调节后，A、B相方波电压占空比分别为45%和29%,达成相电压调节，实现优化两相模态(见图3(e))，A、B相振动模态幅值分别为1.211 μm和1.215 μm，且相位接近π/2。图3(c)、(f)为调节前、后电机输出转矩曲线，调节前转矩曲线在(-0.4 N·m, 0.2 N·m)之间变化，调节后转矩曲线在(-0.05 N·m, 0.04 N·m)之间变化，达到优化效果，即转矩脉动明显减小，提高电机输出精度。

图3 优化控制前、后的相电压、振动模态及输出转矩曲线

以上通过仿真验证滑模观测器的准确性及鲁棒性，并验证基于滑模观测的优化控制，改善电机输出转矩脉动的可行性，需要进一步进行实验验证。

3.2 基于振动模态观测器的电机转矩优化实验分析

实验平台如图4所示，本文通过现场可编程门阵列(FPGA)调节全桥驱动电路方波占空比实现对电机的驱动，并以此实现、验证本文提出的滑模观测器有效，且实现振动模态优化。定子振动模态无法精确检测，但可以通过观察输出转矩脉动间接证明基于观测器输出实现的优化控制有效。

图4 基于FPGA的TWUSM全桥驱动控制实验平台

图5为稳态电压驱动与基于振动模态调节驱动电路占空比的两种控制方式下的相电压与输出转矩曲线。对比调节前、后电机相电压、输出转矩，转矩脉动区间由(-0.62 N·m, 0.49 N·m)减小至(-0.36 N·m, 0.28 N·m)，得到改善，说明实验中对A/B相电压由180 V/196 V调节至212 V/152 V是有效调节，证明定子振动模态得到一定程度改善以及基于相电流搭建滑模观测器可靠。前文提到TWUSM由于工艺、环境等原因参数无法严格对称，导致等幅正交电压无法产生等幅正交振动模态，且实验过程中对于电压的调节趋势为两相电压幅值差变大，与此相互印证，优化振动模态的研究思路具有研究价值。

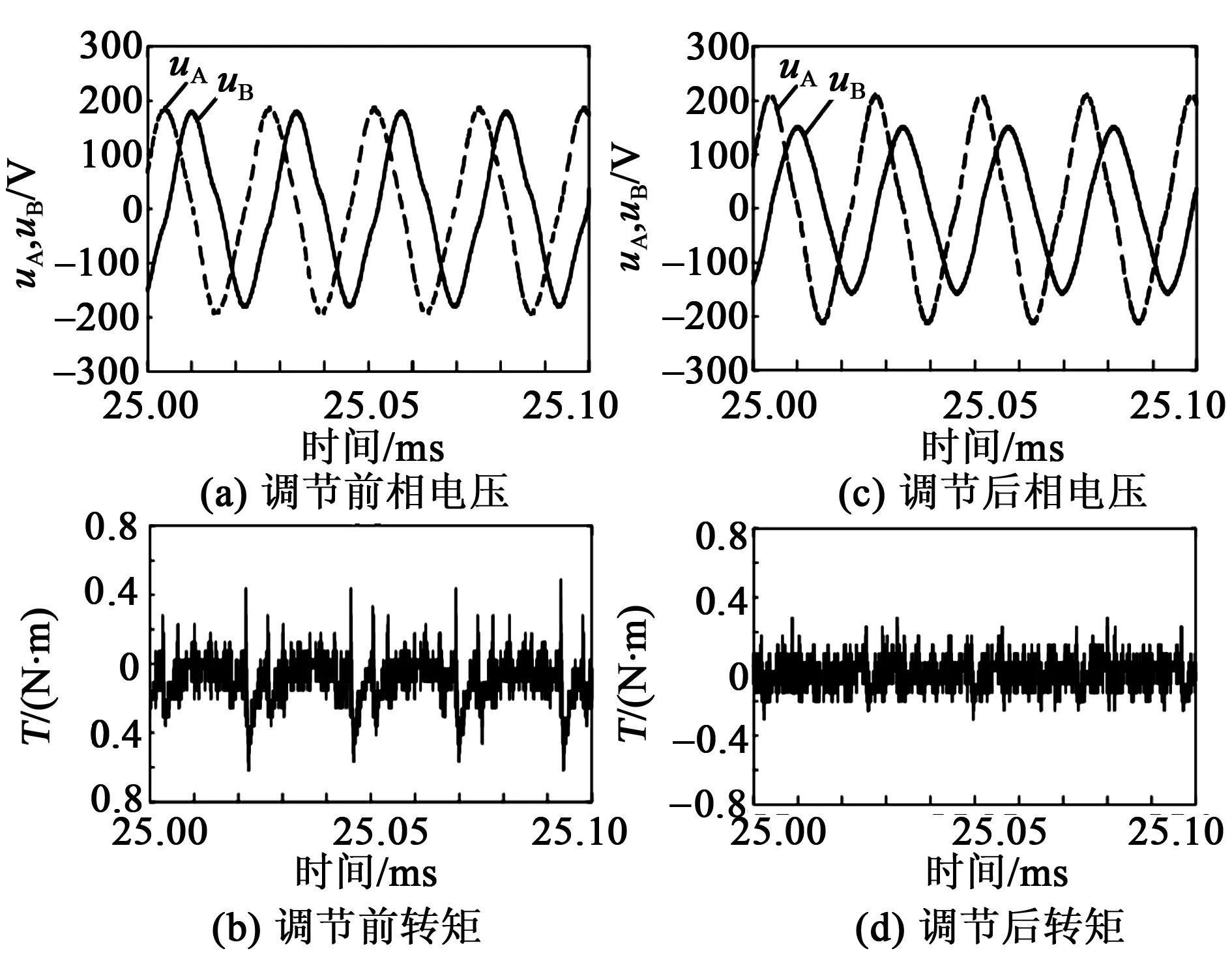
图5 优化控制前、后电压及输出转矩曲线

4 结束语

通过对TWUSM驱动机理分析，考虑TWUSM具有的参数不确定性和严重非线性带来转矩脉动等问题，针对产生驱动的高频振动环节构建了具有鲁棒性的振动模态滑模观测器，本文对滑模观测器的稳定性和鲁棒性进行了理论分析和仿真验证。结果表明，滑模观测器可实现对振动模态的准确观测，且具有参数鲁棒性，并分析了调整电压实现振动模态优化控制的可行性。最后通过仿真和实验验证了基于振动模态滑模观测器对两相电压进行优化调节可有效改善输出转矩脉动。