光滑扩展有限元方法及其特点研究

徐志民， 谢 伟， 窦鹏鹏

(西北工业大学 航空学院，西安 710072)

1 引 言

随着有限元法在工程中的广泛应用，其局限性渐渐凸显。首先，常规有限元法的形状函数是连续的，导致单元内部材料参数不能阶跃，因此分析断裂力学的能力很弱。其次，由于常规有限元法在数值积分过程中需要进行坐标映射，对单元形状有着较高的要求，因此有限单元法在处理畸变网格时表现无力。

为了解决真实结构中存在的疲劳裂纹扩展问题，针对断裂问题的数值分析方法得到了广泛的研究。但是采用常规有限元法进行断裂力学分析时，由于其裂纹尖端存在奇异性，计算易不收敛，必须对裂尖网格进行细化加密处理。另外，在裂纹扩展计算中，裂纹必须沿着已有的网格边线进行扩展，每一步的扩展都需要进行网格重构，增加了计算的负担。所以，为了降低对网格的依赖性，引入了放宽网格负担的离散化技术，扩展有限元法XFEM[1-6]应运而生。XFEM基于单元分解法PUM[7,8]，通过在位移场的基础上添加扩充函数来反映裂尖区域的不连续性。XFEM的不连续界面独立于网格，可以沿着任意角度扩展且无需网格加密和重构，有效弥补了常规有限元法在处理断裂力学方面的不足，但XFEM仍然需要进行坐标映射。Liu等[9]提出了S -FEM，二维 S -FEM 将单元内部的面积分转换为沿着光滑域的线积分，避免了单元的坐标映射(等参转换)和雅可比矩阵计算等问题，降低了常规有限元法对网格质量的依赖性。随后根据光滑应变技术的不同演化出基于节点光滑有限元法NS -FEM、光滑子域有限元法CS -FEM、光滑边域有限元法ES -FEM和光滑面域有限元法FS -FEM。

Bordas等[10]将光滑应变技术CS -FEM应用于XFEM中，通过围线积分，简化了不连续近似积分，避免了在近似中引入Westergaard solution时对奇异函数进行数值积分的需要，其稳定性、鲁棒性和计算成本得到大幅提高。Chen等[11,12]提出将ES -FEM引入到XFEM计算中，将内部积分转化为边界积分，消除了对被不连续切割单元进行细分的需要，简化了数值积分过程，在收敛性、精度和计算效率方面优于标准的XFEM。Vu-Bac等[13]提出NS -XFEM，与ES -XFEM和标准XFEM-T3对比发现，NS -XFEM可以产生超收敛解。Jiang等[14]将ES -XFEM应用于正交异性复合材料的断裂机理分析中，再次证明ES -XFEM比XFEM更准确。Wu等[15]证明了ES -XFEM在二维弹性体动态断裂问题分析中的有效性和效率。Surendran等[5]针对非多项式扩充函数提出了线性光滑技术(Linear smoothing)来近似模拟高阶多项式场。Wan等[16]针对轴对称弱不连续问题，提出了一种完全光滑扩展有限元方法，并在弹性静力学和弹性动力学中证明了方法的可行性。

上述文献只是单独将某一种光滑有限元技术引入到XFEM中进行计算，本文在研究XFEM的基础上结合光滑子域和光滑边域两种方法的优点，提出了一种新的有限元算法，在单元与扩充结点的选取上采用ES -FEM的光滑域划分思想，在数值积分计算刚度矩阵时采用基于三角形子域的 CS -FEM 积分思路。通过拉伸载荷下的纯Ⅰ型边界直裂纹模型，确定S -XFEM中裂尖光滑单元子胞数目、高斯点个数、交互积分区域放大系数及扩充方式等关键参数的选取。通过剪切载荷下纯II型边界直裂纹模型和拉伸载荷下混合边界直裂纹模型，对S -XFEM的实用性和精确性进行研究。

2 S -XFEM基本理论

2.1 光滑应变技术

由常规有限元法可以得到单元内相容应变场的计算公式为[17]

(1)

(2)

利用光滑应变技术创建光滑应变场，光滑应变技术将光滑域内的应变场设定为常量，其大小可通过修正相容应变场获得，也可通过直接对位移场求导得

(3)

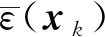
(4)

并且光滑函数必须满足

(5)

2.2 基于CS -FEM的S -XFEM刚度矩阵

(6)

式(6)扩充项的位移值可通过位移扩充函数使位移在结点处的值等于结点位移，本文选用一种经典的修正方案,

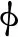
(7)

式中 第一个扩充项含有一个阶跃函数(Heaviside jump function)H(x)，在裂纹的上方取+1，在裂纹的下方取-1，其数学表达式为

(8)

式中x为问题点(高斯点)，x*为裂纹线上离x最近的一个点，n为裂纹在x*点处的单位外法线向量。

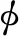
(9)

式中 (r,θ)为裂尖处的局部极坐标系。

(10)

(10)

(11)

(11)

(12)

(12)

所以系统总体刚度矩阵可以表达为

(13)

式中Ns为光滑域个数。

(14)

2.3 基于ES -FEM的S -XFEM扩充结点选择

如图1(a)所示，含有裂尖的光滑域用网格线标识，称为裂尖光滑域，该光滑域所在的两个单元的所有结点为裂尖结点Nes -asympt，用圆圈标识。裂纹贯穿的光滑域的支持结点为贯穿结点Nes -disc，用三角标识。可以发现，相比于XFEM的结点类型选择，基于ES -FEM的选择方案可以增加裂尖结点的个数。

2.4 S -XFEM的积分策略

CS -FEM的光滑子域完全在单元内部，所以其单元刚度矩阵积分域与FEM中所使用的积分域一致，避免对ES -FEM的一个光滑域中分属不同单元的光滑子域的形函数的单独计算，确保一个光滑域内所有高斯点的形函数可以在同一个单元中计算。所以S -XFEM与ES -FEM的最大区别在于进行计算的光滑域的不同，如图1所示。图1(b)为基于S -XFEM的光滑单元的划分方案。与XFEM相似，S -XFEM也有5种积分区域，即裂尖光滑单元、贯穿光滑单元、裂尖混合光滑单元、贯穿混合光滑单元和常规光滑单元[11,12]。

裂尖光滑单元，由于被积函数为非多项式，简单地将光滑单元划分为多边形子域进行计算无法达到数值精度要求，所以需要在裂尖附近使用更多的积分点。通过以下步骤实现。(1) 使用XFEM中Delaunay三角化将光滑单元划分为三角形子域sub -sd1～sub -sd5； (2) 将三角形子域进一步划分为ns c个子胞，图2(a)显示了将sub -sd1和sub -sd2划分为3个子胞的情况，sub -sd1和sub -sd2分别划分为sc1～sc3和sc4～sc6； (3) 在每个子胞边界上进行积分。当在共用一条裂纹的两个子胞(sc3和sc5)上布置高斯点进行积分时，阶跃函数和裂尖扩充函数虽然在两个子胞上的计算值相同，但在裂纹处的位移实际上却是不连续的。所以在计算时不使用高斯点坐标，而使用子胞形心坐标。与常规光滑有限元相比，由于裂尖附近的梯度很大，所以需要在边界上使用更多的高斯积分点，图示每个子胞边界上使用5个高斯积分点。

图1 基于ES -FEM和S -XFEM的扩充光滑域和结点选择方案

贯穿光滑单元，将裂纹贯穿的光滑单元沿着裂纹线划分为若干个子域，使得每个子域上被积函数连续可微。与XFEM类似，在S -XFEM中同样需要将非三角形多边形使用Delaunay三角化为三角形子域，如图2(b)所示，贯穿单元划分为sub -sd1～sub -sd3三部分。线性形函数与阶跃函数的乘积NiH在外部边界和内部边线上是线性的，所以在贯穿光滑单元的光滑子域边界上使用一个高斯点即可。

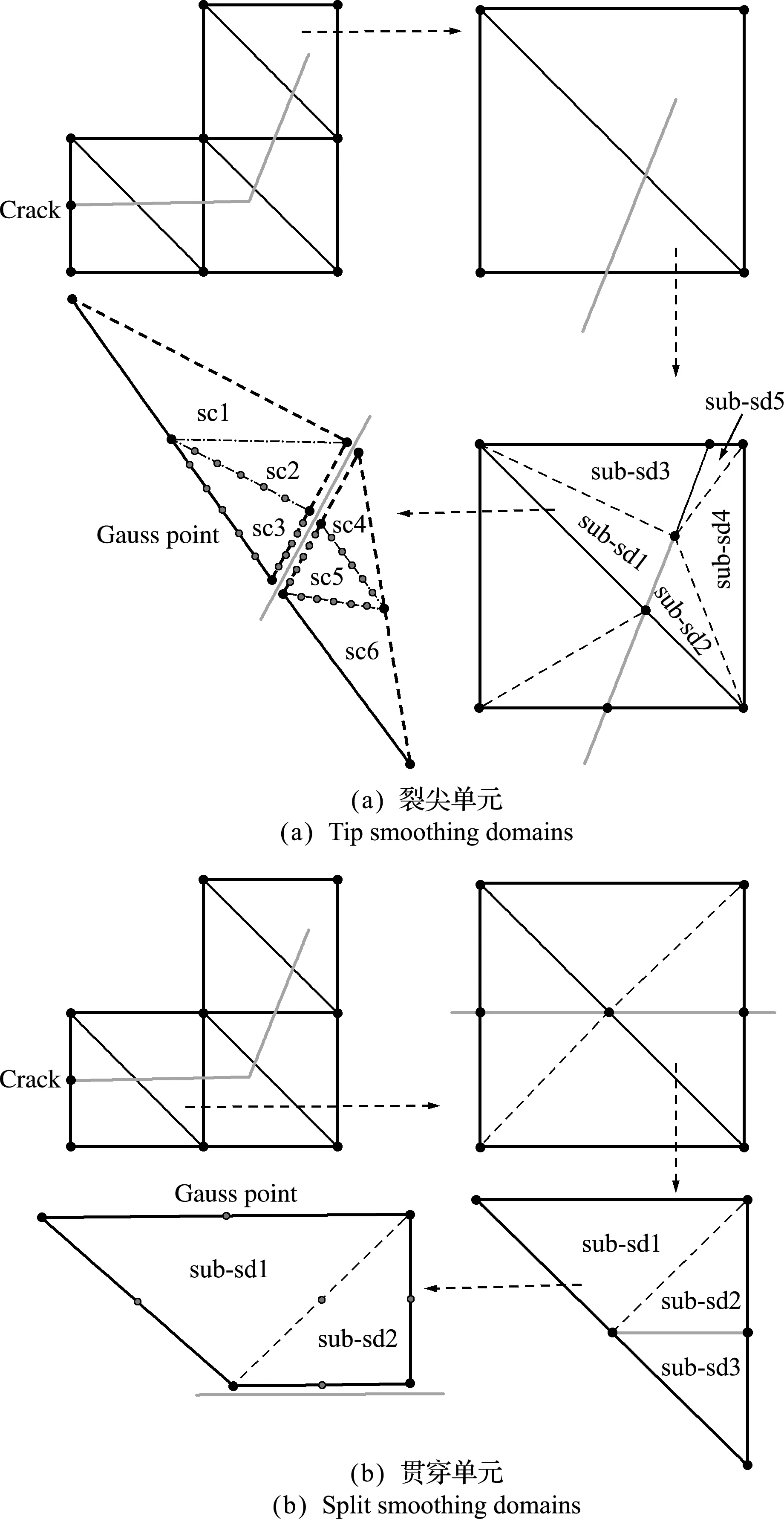
图2 裂尖单元和贯穿单元的子域划分方式

裂尖混合光滑单元和贯穿混合光滑单元使用的积分策略和文献[11,12]的一样，本文不再复述。

3 数值分析结果

3.1 拉伸载荷下的边界直裂纹

采用一个承受拉伸载荷作用的边界直裂纹算例[11,12]研究上述算法。材料参数为杨氏模量E=30 GPa，泊松比υ=0.3，假设为平面应变问题。

平板的尺寸为1 m×2 m，边界直裂纹长度为a，在上边界施加σ=1.0 Pa的拉伸应力。平板底部边界施加y方向上的位移约束，底部左端点同时施加x和y方向的位移约束。模型的几何、载荷和边界条件如图3(a)所示，T3和Q4网格划分如图3(b，c)所示，图示网格布种个数为20×40。

文献[18]给出了该模型应力强度因子的精确解：

(15)

式中C为几何修正系数：

C=1.12-0.231(a/b)+10.55(a/b)2-

21.72(a/b)3+30.39(a/b)4

(16)

3.1.1 S -XFEM裂尖光滑单元光滑子胞数目

和高斯点数目的影响研究

关于高斯点个数对应力强度因子的影响已经在文献[11,12]给出，因此，本文不再进行讨论，直接引用文献的结论，选取光滑子胞边界高斯点数目ngau=5。

CS -FEM在计算静力学问题时其精度会随着子胞个数的改变而发生较大的变化，当子胞个数ns c=4时计算结果最接近于解析解[19]。由于本文扩充函数的引入，子胞个数对于结果的影响不能直接引用已有结论，下面对光滑子胞个数对裂尖光滑单元积分结果的影响进行讨论。

图3 拉伸载荷下边界直裂纹模型及网格划分

采用本节计算模型，取a=0.6 m，划分70×140个结点，裂尖采用拓扑扩充，交互积分所使用的半径放大系数rk=5。图4为Q4裂尖单元内使用不同子胞个数时的划分结果。表1为S -XFEM使用T3和Q4单元计算的应力强度因子随子胞个数的变化情况。由表1可知，KI的计算值始终小于解析解，随着ns c的增加，KI越来越小并逐渐收敛于固定值。由于ns c=1时,KI与最终收敛的固定值相差较大，计算结果存在不稳定性。所以综合考虑，本文认为ns c=2时，S -XFEM可以取得较为稳定且精确的数值解。

因此，本文如不特殊说明，选取ngau=5，ns c=2。

3.1.2 交互积分区域半径放大系数的影响研究

使用交互积分法计算应力强度因子，需要确定一个特征长度的放大系数rk。采用3.1.1的模型，计算结果列入表2。当rk很小时计算结果波动很大，这是因为交互积分区域靠近裂尖，裂尖扩充结点使计算结果分散性很大，随着rk的逐渐增大，积分区域离裂尖越来越远，计算结果趋于稳定，当rk=5时，4种方法的结果均收敛于稳定值。因此，本文如不特殊说明，取交互积分区域半径放大系数rk=5。

表1 不同ns c下的KI计算值和解析解

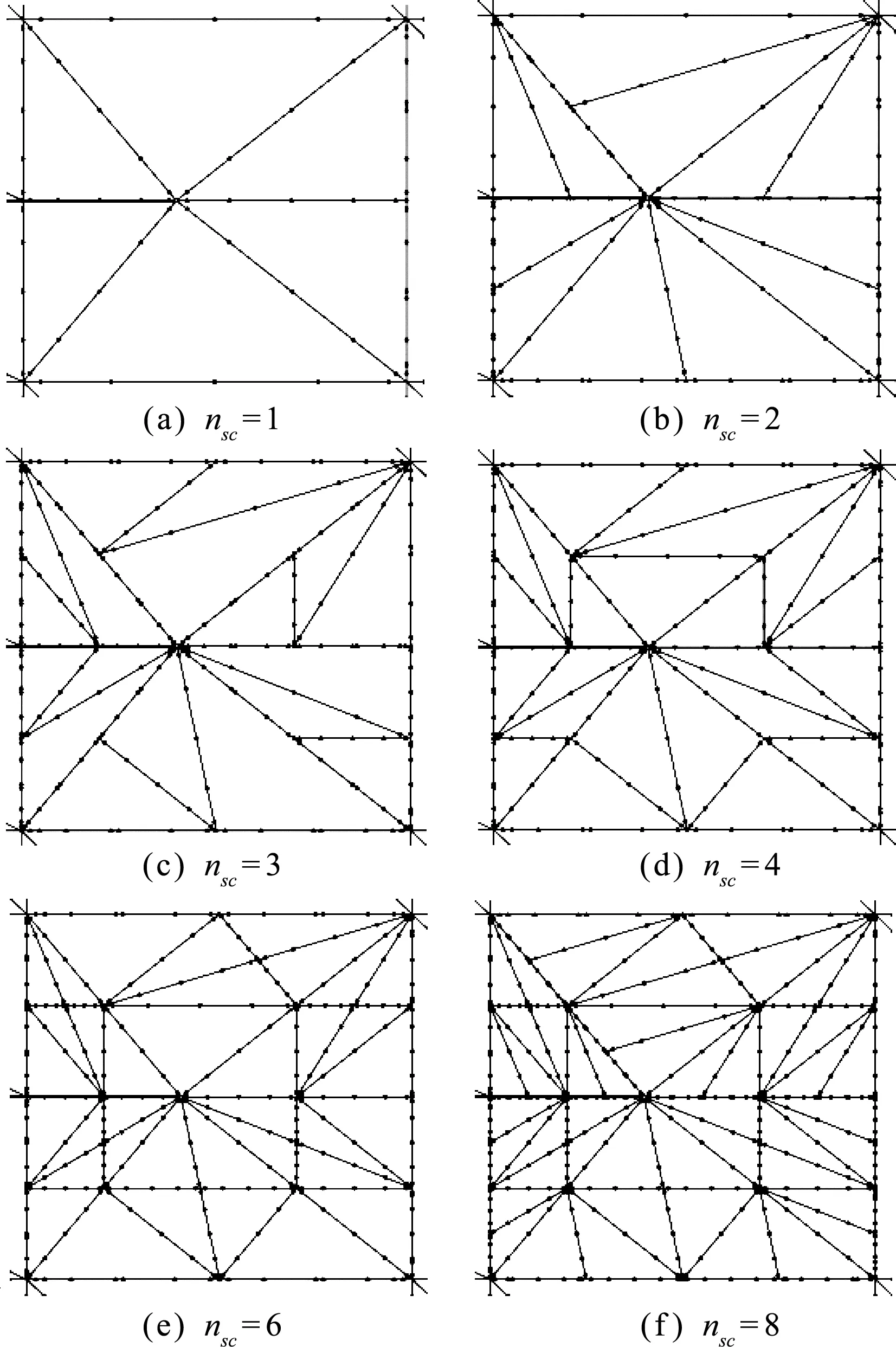
图4 裂尖Q4单元子胞划分

3.1.3 扩充方式的影响研究

基于二维几何的裂尖扩充，以裂尖为圆心定义一个半径为r的圆，在此区域内的结点都用裂尖扩充函数扩充。半径r的定义为r=rehlocal，re为几何扩充半径的放大系数。拓扑扩充只扩充含有裂尖的单元结点。

采用3.1.1的模型，图5给出了Q4使用不同扩充方式下的结点扩充示意图，图中方框为裂尖扩充结点，叉形为贯穿扩充结点。不同扩充方式下应力强度因子的计算结果列入表3。可以看出，re=1时拓扑扩充与几何扩充的计算结果相同，因为这时几何扩充半径内的结点与拓扑扩充一致。随着re的增大，KI计算值增大并趋近于解析解，这是因为re的增大使得扩充结点增加，裂尖扩充函数作用更加明显，相应的计算结果也就更加精确。当re进一步增加时，计算误差突然增大，这是因为在交互积分半径放大系数(rk=5)一定的情况下，裂尖扩充结点范围的增大使得交互积分区域内包含了裂尖结点，从而降低了KI的计算精度。另外，由于ES -FEM结点的支持域比XFEM大，所以相比于XFEM，其对几何扩充半径放大系数re更为敏感。因此面对不同需求时可以选择不同的单元扩充方式。

图5 不同扩充方式下Q4结点扩充

3.1.4 精确性与收敛性研究

对比S -XFEM和XFEM在分别使用T3和Q4单元时应力强度因子的计算结果，以研究不同算法的精确度与收敛性。采用3.1.1的模型，裂纹长度选为0.3 m和0.6 m。图6和图7分别给出了4种方法应力强度因子计算值随着结点数增加的变化趋势和其相对误差随结点数增加的变化趋势。

表2 不同交互积分半径放大系数下的KI计算值Tab.2 Stress intensity factor under different rk

表3 不同扩充方式下的KI计算值Tab.3 Stress intensity factor under different extended modes

图6 结点数对应力强度因子计算值的影响

图7 结点数对应力强度因子计算值相对误差的影响

从图6可以看出，当裂纹长度a=0.3 m和 0.6 m 时，四种方法计算的KI随结点数的增加均收敛于解析解，当结点数为 70×140 时，所有方法的相对误差都控制在5%左右，当结点数为100×200时，XFEM-Q4方法的相对误差在两种裂纹长度下分别可以达到0.309%和0.508%。通过比较可以看出，XFEM的计算精度和收敛速度稍优于 S -XFEM，相同算法下，Q4单元的计算精度和收敛速度稍优于T3单元。

3.1.5 不规则网格的影响研究

采用不规则网格检验S -XFEM程序对网格的依赖性，不规则网格采用式(17)随机生成：

(17)

式中x和y为初始规则网格结点的坐标值，Δx和Δy为单元直角边在x和y方向的长度，rd为在[-1,1]内变化的随机数，α为单元奇异系数。

通过改变α值可以生成不同程度的不规则网格，如图8所示，采用3.1.1的模型。逐渐增加不规则因子α以计算不同网格畸变程度下的KI，计算结果相对误差如图9所示。可以看出，S -XFEM的精确度虽然没有XFEM高，但S -XFEM在不规则网格下的稳定性要明显优于XFEM，其计算结果几乎不受网格畸变程度的影响，而XFEM计算结果波动较大。在实际的计算中，当α=0.12时，XFEM-T3出现了三点几乎共线的细长单元，凸包计算无法完成，这直接导致了程序的崩溃。S -XFEM对畸变网格的特性将十分有助于分析大变形问题。

3.2 剪切载荷下的边界直裂纹

使用一个承受剪切载荷的边界直裂纹算例对算法的精确性和收敛性进行进一步研究。材料参数为杨氏模量E=30 GPa，泊松比υ=0.3，假设为平面应变问题。平板的尺寸为16 mm×7 mm，边界直裂纹长度a=3.55 mm，在上边界施加大小为τ=1.0 Pa的剪切应力。平板底部边界施加y方向上的位移约束，底部左端点同时施加x和y方向的位移约束。模型的几何、载荷、边界条件以及T3和Q4网格(结点数20×40)如图10所示。文献[18]给出了该问题的应力强度因子参考解：

(18)

裂尖单元采用拓扑扩充，ngau=5，ns c=2，rk=5。图11和图12分别给出了随着网格数的增加，四种方法计算的KI、KII和相对误差的变化规律。可以看出，这四种方法计算的KI和KII随着结构结点数的增加，均能收敛于解析解。当结点数为 60×120时，所有方法的相对误差都控制在5%左右；当结点数为100×200时，XFEM-Q4方法的相对误差分别为0.494%和1.397%。通过比较可以看出，XFEM的计算精度和收敛速度稍好于S -XFEM，相同算法下，Q4单元的计算精度和收敛速度稍好于T3单元。对比3.1节的结果，可以发现S -XFEM方法在计算精度上与XFEM的差距有大幅减小，其数值计算精度几乎与XFEM相当。

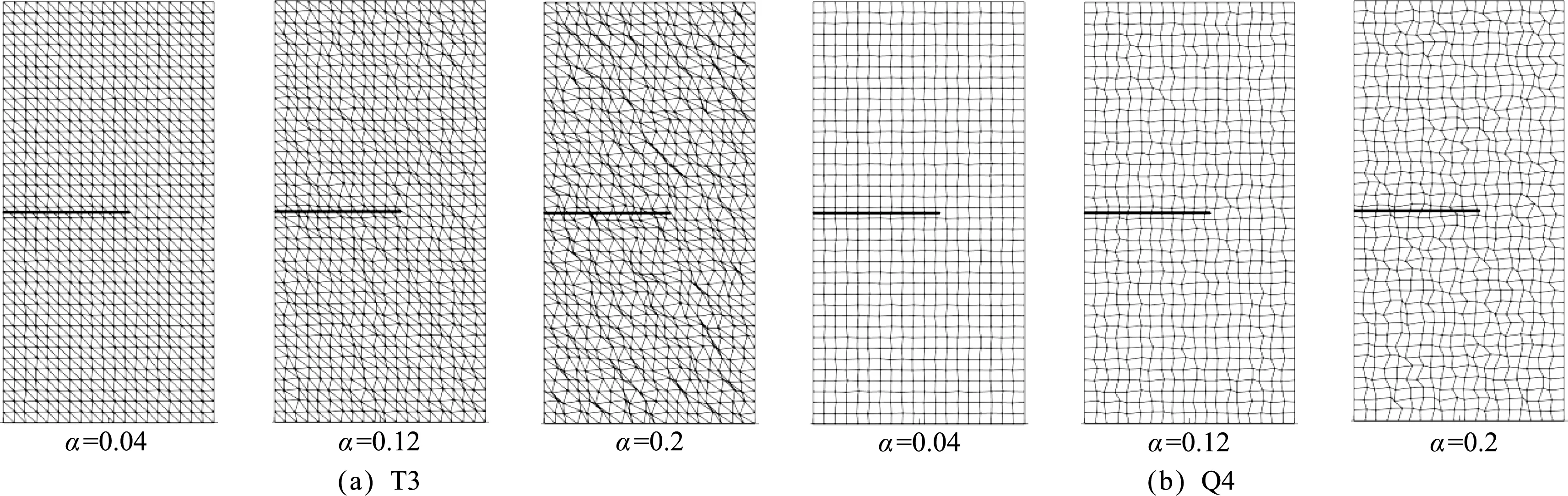
图8 不同α值下的三角形和四边形网格

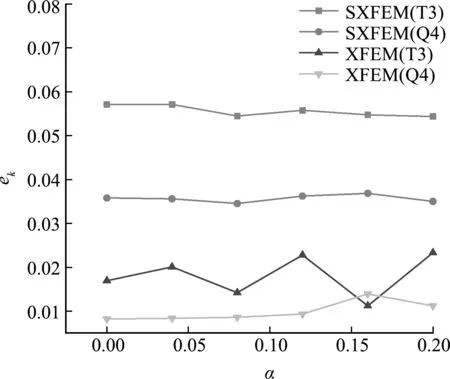
图9 单元奇异系数α对相对误差ek的影响

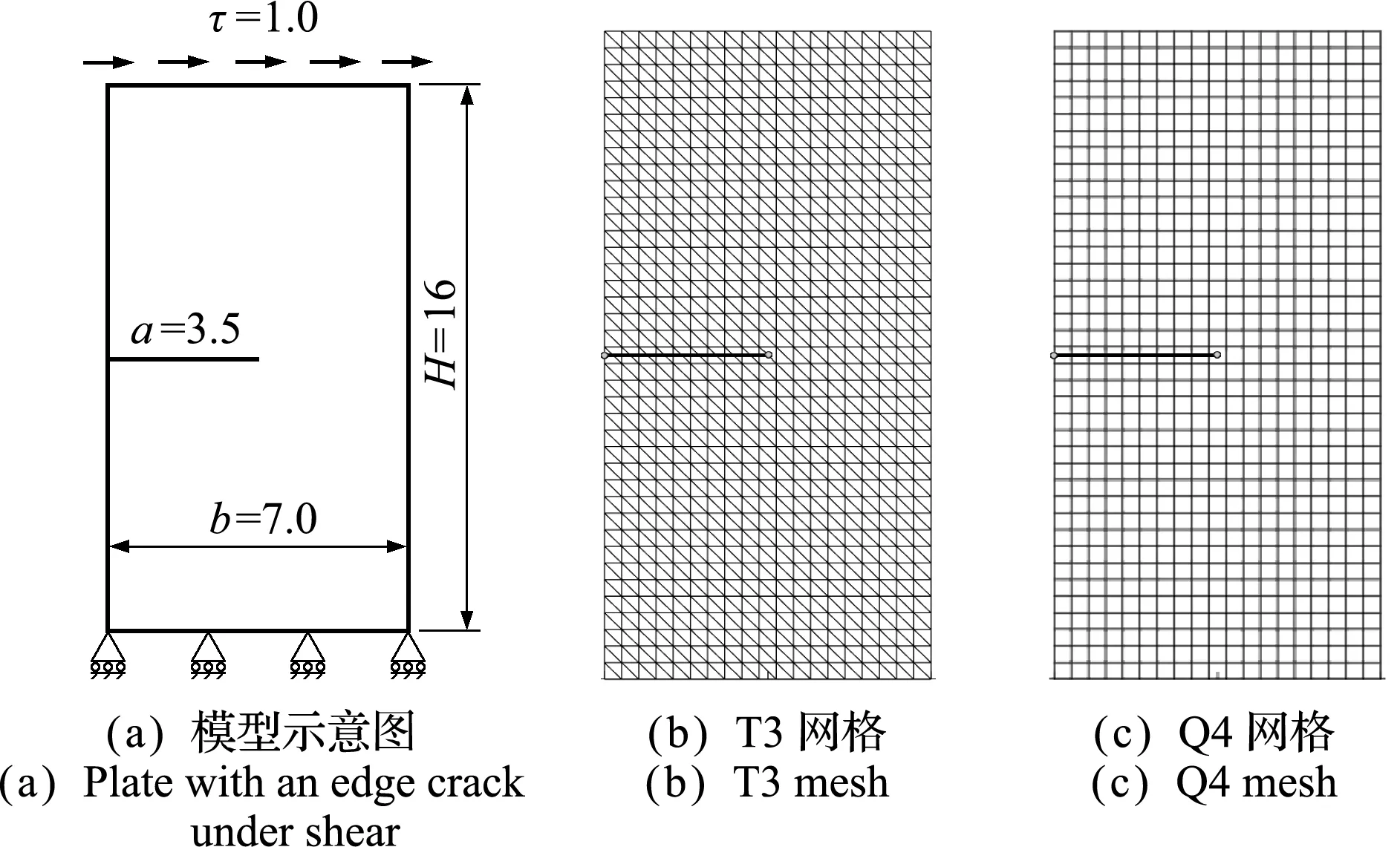
图10 剪切载荷下边界直裂纹模型及网格划分

3.3 拉伸载荷下的边界斜裂纹扩展问题

使用一个承受拉伸载荷作用的边界斜裂纹扩展算例验证本文S -XFEM程序在处理连续扩展时的特性。材料参数为杨氏模量E=30 GPa，泊松比υ=0.3，假设为平面应变问题。平板的尺寸为1 m×2 m，含有与水平成30°夹角的边界斜裂纹，裂纹初始坐标为(0,0)和(0.3，0.173205)。在上边界施加大小为σ=1.0 Pa的拉伸应力。平板底部边界施加y方向上的位移约束，底部左端点同时施加x和y方向的位移约束。模型的几何、载荷和边界条件如图13(a)所示，设定扩展步长为0.03 m，扩展步数为10。图13(b，c)为该模型使用三角形网格和四边形网格划分示意图(图示布种为20×40)，实际计算使用布种数为100×200。

图11 结点数对应力强度因子计算值的影响

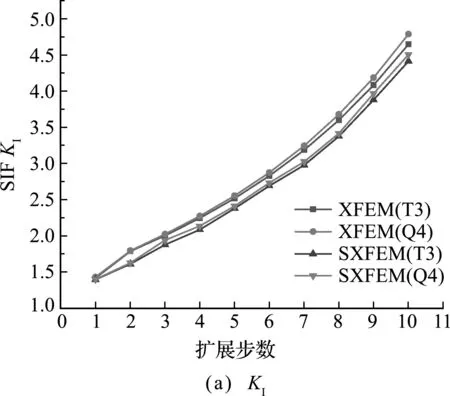
图14给出四种方法计算裂纹扩展过程中的应力强度因子KI和KII的值。可以看出，随着裂纹的向前扩展，KI值均逐渐增大，KII值均逐渐收敛于0，裂纹保持水平扩展，裂纹转换为纯II型。

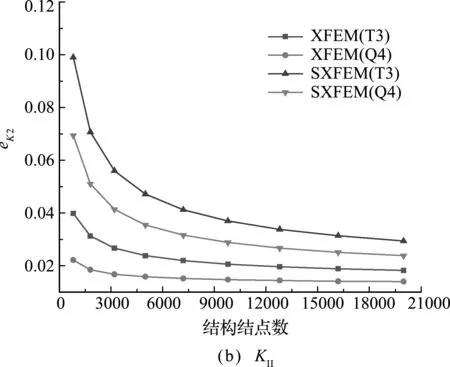
图12 结点数对应力强度因子计算值相对误差的影响

图13 拉伸载荷下边界斜裂纹扩展模型及网格划分

4 结 论

本文主要研究了求解二维平面问题的S -XFEM，详细阐述了其基本理论并推导数值积分公式，给出了光滑域内高斯点的积分策略，设计并编制了算法的有限元计算程序，采用经典算例验证并与XFEM对比。光滑应变技术的运用使得在计算单元刚度矩阵的过程中无需对各点的形函数进行求导，所以在S -XFEM中也无需对扩充项求偏导，从而避免了对极坐标函数求偏导数的复杂过程，有效地简化了单元刚度矩阵的计算过程。主要的研究内容和结论如下。

(1) 将子域光滑应变技术和边域光滑应变技术扩展到XFEM的框架中，建立了一种新的 S -XFEM，在单元及扩充结点选取时采用ES -FEM的光滑域划分方式，在数值积分计算刚度矩阵时采用基于三角形子域的CS -FEM积分思路。该方法通过光滑域将内部积分转化为边界积分，消除了对受不连续结构切割单元进行细分的需要。而且，通过应变平滑技术，计算刚度矩阵时不再需要对形函数求导，避免了裂尖奇异点的出现，极大简化了计算过程。

(2) 计算结果表明XFEM和S -XFEM均有很高的计算精度和稳定的收敛性，XFEM略优于S -XFEM，而S -XFEM对于不规则网格的适应性要明显强于XFEM，可以很好地应用于大变形问题分析，甚至是动态分析。本文提出的S -XFEM对于纯II型裂纹、裂纹扩展模拟皆有很好的计算结果，说明本文编制的S -XFEM程序是有效的。