攒尖四坡屋面风致雪漂移的数值模拟

颜卫亨， 姬明辉， 代 鹏， 张玉杰

(1.长安大学 建筑工程学院，西安 710061； 2.青岛万科房地产有限公司，青岛 266071

1 引 言

风雪天气中，雪颗粒在风的作用下将发生复杂的漂移堆积运动，造成建筑屋面积雪不均匀分布，可能导致雪荷载局部超载，从而发生破坏。而我国现行《建筑结构荷载规范》(GB 50009-2012)[1]条文说明7.2.1指出,根据以往设计经验，参考国际标准ISO 4355及国外有关资料，对屋面积雪分布仅概括地规定了典型屋面积雪分布系数，表明我国规范对屋面积雪分布系数的规定并未经过系统验证，其合理性有待商榷。对于坡屋面的积雪分布系数，我国荷载规范主要参考美国规范(ACSE 7-10)[2]和欧洲规范(BS EN1991-1-3)[3]进行修订，其规定偏于简单，未对屋面进行详细分区，而实际环境中由于侵蚀和沉积的发生,屋面各处积雪分布不均匀，只用一个积雪分布系数无法描述整个屋面的积雪情况。同时，各国荷载规范涉及的屋面类型均有限，关于坡屋面只有单坡和双坡两种，未对攒尖四坡这种体型做出规定。攒尖四坡房屋广泛应用于民用和野营房屋，当其自重较轻时，对风雪作用较敏感，结构设计时风雪荷载通常是控制荷载，尤其是风作用下的不均匀雪荷载影响更大，而其在设计时只能近似参照其他体型，理论研究滞后于工程应用，但积雪分布状态与体型息息相关，不同体型屋面积雪分布差异很大，这种做法可能造成设计不合理或存在安全隐患。因此，对攒尖四坡屋面风致雪漂移进行研究具有重要的理论意义及工程应用价值。在工程中使用的攒尖四坡房屋往往具有不同屋面坡度，环境中的风速和风向角也在不断变化，故本文从风向角、风速和屋面坡度三方面对攒尖四坡屋面风致雪漂移规律进行分析。

风致雪漂移运动可通过现场实测、风洞试验和数值模拟三种方法开展研究。实地观测因受自然条件影响较大，应用较少，而《建筑工程风洞试验方法标准》(JGJ/T 338-2014)[4]指出,在研究风致雪漂移问题时，风洞试验常对仪器设备有特殊要求，或难以满足相似性，而数值模拟是研究这种流动现象的有效手段。数值模拟方法具有比较突出的优点,成本低且周期短，不必考虑相似性条件，可以方便地改变各种参数和变换各种体型等。文献[5，6]分别模拟了大跨膜屋面和平屋面上的风致积雪分布情况，Boutanios等[7]提出一种新型的双向耦合欧拉-欧拉模拟方法，其他学者也对风致雪漂移运动进行了大量数值模拟[8-11]，但关于攒尖四坡屋面风致雪漂移的研究鲜见报道，目前的研究多针对大跨结构、立方体、高低屋面以及平屋面等特定外型的结构，所得结果并不能直接应用于攒尖四坡屋面。因此，本文从风雪运动特性和参数选取等方面进行分析，得出适用于此类房屋的数值模拟方法。

2 数值模拟的基本理论

2.1 雪颗粒的运动及物理特性

雪颗粒的运动模式按其离开地面的高度分为蠕移、跃移和悬移三类，如图1所示。研究表明，蠕移运动引起的雪颗粒传输量较少，跃移和悬移运动是雪粒传输的主要途径，因此本文在建立数值模型时忽略蠕移运动，只考虑跃移和悬移。

不同的雪粒直径和密度大小对其运动规律影响很大，表1列出我国新疆天山地区不同种类雪粒的直径及密度取值，《建筑结构荷载规范》(GB 50009-2012)[1]指出，我国大部分地区(东北及新疆北部地区，淮河、秦岭以南地区等)积雪的平均密度取150 kg/m3，故参考表1的湿新雪状态，选取雪颗粒直径为0.15 mm、积雪密度为150 kg/m3。参考Tominaga等[12]的研究，将雪粒沉降速度取为0.2 m/s，壁面粗糙高度取为3×10-5m。

2.2 控制方程

风致雪漂移是一种包含气相和固相的两相湍流运动，本文采用单向耦合方法，即空气相为主相，雪相为次相，雪在风的作用下发生漂移和堆积，而雪的运动对风不造成影响。基于欧拉-欧拉方法，采用计算速度较快、稳定性较好的Mixture模型来模拟风雪流。在Fluent软件中，Mixture多相流模型对风雪运动的模拟主要通过三个控制方程来实现，一是基于质量守恒定律提出的连续性方程，二是基于牛顿第二运动定律提出的动量方程，三是雪相体积分数方程，如式(1～3)：

图1 雪颗粒运动

(1)

(2)

(3)

2.3 积雪的侵蚀与沉积

侵蚀与沉积现象的发生取决于壁面摩擦速度，当摩擦速度高于阈值摩擦速度时，雪颗粒受气流影响脱离积雪面进入空气，地面积雪量减少，这一现象称为侵蚀；反之，当摩擦速度低于阈值摩擦速度时，空气中漂浮的雪颗粒进入积雪面，地面积雪量增多，发生沉积。侵蚀量qero和沉积量qdep分别计算为

(4)

3 数值模型的建立

3.1 边界条件

入口边界条件选择速度入口，采用指数律风速剖面，表示为

U(z)=U0(z/z0)α

(5)

式中U(z)为z高度处的平均风速,U0为标准参考高度处的平均风速,z为距地面任一高度,z0为标准参考高度，我国现行荷载规范取为10 m,α为地面粗糙度指数，根据攒尖四坡房屋的使用场地要求，选取B类地貌进行模拟。

出口边界条件采用完全发展的自由出口，计算域顶面及两侧边界采用自由滑移壁面，地面及建筑物表面边界采用无滑移壁面。

3.2 计算域尺寸及网格划分方式

《建筑工程风洞试验方法标准》(JGJ/T 338-2014)[4]规定：数值模拟中计算域入口至模型的距离不宜小于模型最大尺度的10倍，模型至计算域出口的距离不宜小于模型最大尺度的15倍。经过试算，将计算域尺寸取为30L×15L×10H(L为模型最大尺度，H为模型高度)，顺风向模型置于距入流面1/3流域长度处，横风向置于计算流域的中点。立方体模型的计算域即为30 m×15 m×10 m，如图2所示。

在模拟风雪流时，需要格外关注房屋附近的区域，因此采用分区混合网格的划分方式。在模型附近的核心区，单元类型选择Tet/Hybrid，即四面体非结构网格，并利用壁面函数对立方体表面网格进行加密，网格最小尺寸取0.02 m，增长比取1.2，网格尺寸由模型壁面向外逐渐增大。在远离模型的非核心区采用具有规则拓扑结构的六面体结构化网格进行离散，单元类型选择Hex/Wedge，网格尺寸取0.24 m，网格总数为95万。这种划分方式既能准确描述建筑物周围的流场信息，又能控制网格整体数量，提高计算效率。

3.3 湍流模型

Fluent软件为用户提供了多种湍流模型，现选取常用的k-kl-ω，SSTk-ω，RNGk-ε，Realizablek-ε和Standardk-ε五种模型进行模拟并与Oikawa等[13]的实测数据对比，结果如图3所示。为方便分析比较，纵坐标用无量纲雪深S/Sd表示，S为测点处的积雪深度，Sd为远处水平地面四周无遮挡情况下的标准雪深，取Sd=300 mm，S/Sd大于1表示该位置发生沉积，小于1表示发生侵蚀。横坐标以立方体边长(H=1 m)为基准进行无量纲化，X/H=±0.5和X/H=0分别代表立方体的表面和中心截面。

图2 立方体模型计算域尺寸

从图3(a)可以看出，对于顺风向，在A区即立方体迎风侧，k-kl-ω湍流模型与实测值的整体趋势较为吻合，无量纲雪深S/Sd沿着吹风方向先减小后增大，侵蚀沉积规律表现为沉积逐渐减少并转变为侵蚀，且侵蚀先增多后减少，而另外四种湍流模型与实测值相差甚远。k-kl-ω湍流模型与实测值的峰值出现的位置接近，沉积量最大值均出现在X/H=-1.5处，侵蚀量最大值在X/H=-0.85～-0.75之间。在B区即立方体背风侧，除Standardk-ε湍流模型外，其他四种模型的侵蚀沉积规律与实测值基本一致，从立方体表面到远处，无量纲雪深S/Sd随着距离的增大逐渐减小，即沉积逐渐减少，侵蚀逐渐增多。相比四种湍流模型，k-kl-ω湍流模型更为接近实测值。

从图3(b)可以看出，对于横风向，在立方体两侧即C区和D区，k-kl-ω湍流模型与实测结果呈现出一致的侵蚀沉积规律，从立方体表面到远处，无量纲雪深S/Sd先减小后增大，峰值出现的位置也比较接近，最大沉积发生在立方体表面处，最大侵蚀发生在Y/H=±1.0附近，而其他四种湍流模型与实测结果偏差较大。

图3 立方体模拟结果与实测值的对比

综上所述，k-kl-ω湍流模型的模拟结果在立方体表面及其附近与实测值较为吻合，虽然在远离立方体的位置处有一定误差，但是在实际生活中，人们通常更关心建筑物表面及周边的积雪分布情况，故k-kl-ω湍流模型适于模拟建筑物的风雪效应。

3.4 高低屋面上积雪分布的模拟

在此基础上，为验证应用数值模拟方法研究攒尖四坡屋面风致雪漂移运动的合理性，对高低屋面模型进行模拟，并将低屋面中线上的积雪分布结果与Tsuchiya等[14]的实测数据对比，实测中的高低屋面模型尺寸及风向如图4所示，图中H取0.9 m。

图5给出低屋面迎风时，其中线上积雪分布的数值模拟结果与Tsuchiya等[14]的实地观测结果对比情况。可以看出，模拟效果较好，两条曲线的整体趋势相似，无量纲雪深S/Sd先减小后增大，随后又逐渐减小至0。数值模拟结果与实测结果无量纲雪深的极小值分别为0和0.25，两者出现的位置比较接近，均位于X/H=0.3附近；数值模拟结果与实测结果无量纲雪深的极大值大小相近，约为 1.25，但所在位置稍有不同，前者位于X/H=1.1处，后者位于X/H=0.6处。另外，在X/H=0.1～0.2和X/H=1.25～2.25范围内，两条曲线吻合度较高，几乎重合。值得注意的是，在高低屋面交界位置，即X/H=0处，模拟值为0.85，远小于实测值的1.9，出现这种现象的原因可能与实测中的风向和风速无法保持在某个固定数值，而是在一定范围内变化有关。

图4 高低屋面模型尺寸及风向

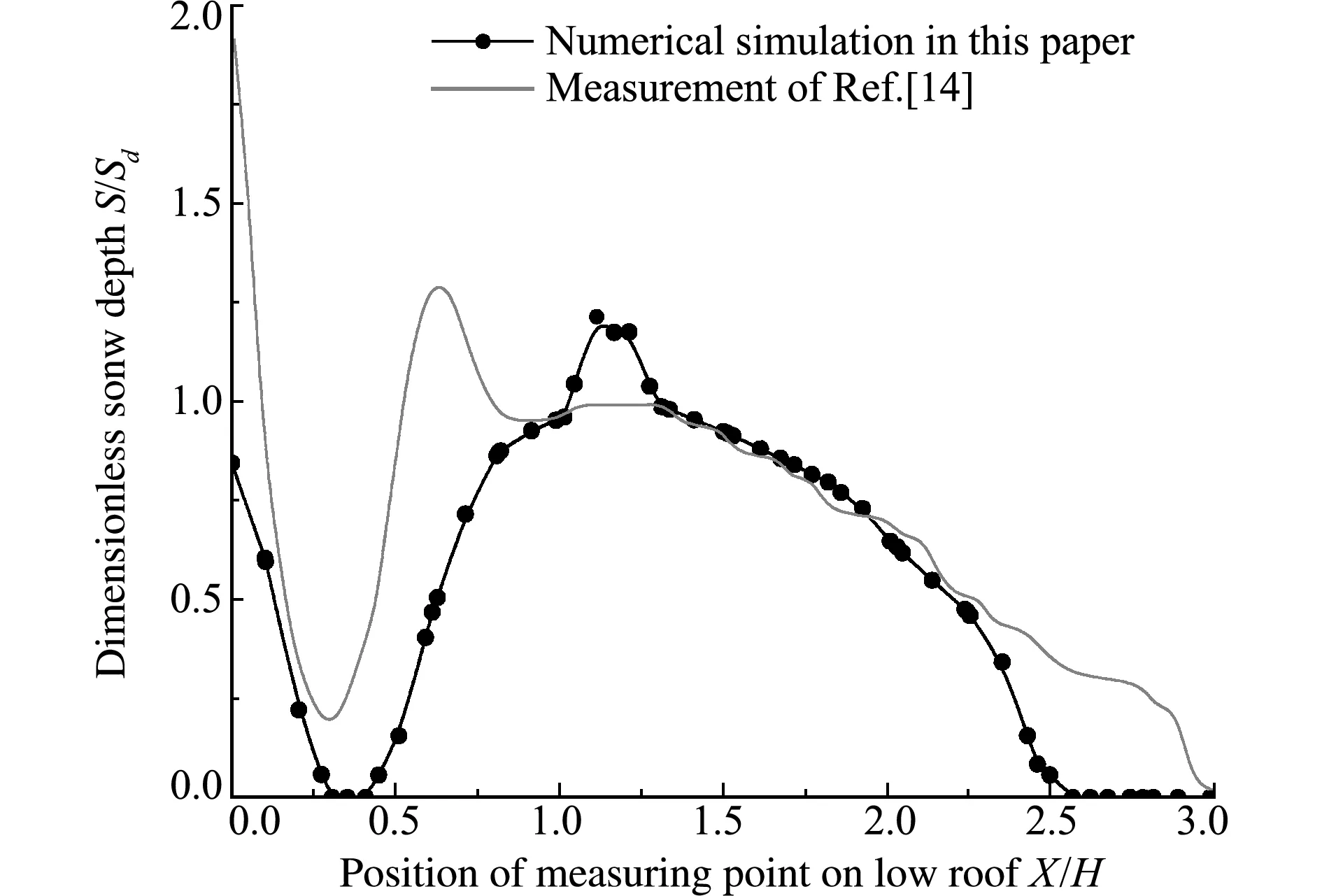
图5 高低屋面模拟结果与实测值对比

图6为文献[15]的高低屋面风洞试验结果，给出不同风速下低屋面积雪分布，可看出风洞试验结果与Tsuchiya等[14]的实测值相差较大，相比之下，本文的模拟结果更接近实测值。通过以上对比分析可知，利用数值模拟技术可以有效模拟屋面上的风致雪漂移运动。

4 攒尖四坡屋面风致雪漂移的数值模拟

为获得攒尖四坡屋面在风雪共同作用下的积雪分布规律，以某研究所设计开发的攒尖四坡野营房屋为研究对象，如图7所示，以风向角、风速和屋面坡度为分析参数进行数值模拟。由于攒尖四坡房屋双轴对称且各边长均相等，故只需模拟0°～45°之间的风向角，以15°为间隔，如图8所示。通过实地观测、风洞试验和数值模拟对风致雪漂移现象进行大量研究发现，当风速达到5 m/s左右时雪

图6 文献[15]的风洞试验结果

图7 攒尖四坡房屋外观

漂现象开始出现，我国规范《野营帐篷》(GBT 27735-2011)[16]4.2.8.3条规定,帐篷应能在风速为15 m/s任何风向的风中保持竖立，因此本文将模拟风速取为5 m/s～15 m/s，以2 m/s为间隔。根据帐篷使用功能及人员活动空间的要求，屋面坡度选择25°，30°，34°，40°和45°五种，其中34°为攒尖四坡房屋的原始坡度。

利用屋面积雪分布系数来研究攒尖四坡屋面积雪变化规律，屋面积雪分布系数为屋面水平投影面积上的雪荷载与基本雪压的比值，即地面基本雪压换算为屋面雪荷载的换算系数。结合屋面雪深分布云图，各分区的积雪分布系数可由式(6)求出

(6)

4.1 屋面分区设计

我国荷载规范对于双坡房屋的不均匀雪荷载，是以屋脊为界划分为不同区域，本文参考这种物理分区方法，将攒尖四坡屋面以屋脊为界限初步分为A、B、C和D四个区域。为方便描述屋面积雪分布规律，对屋脊进行规定，如图8所示。

试算风向角为0°、风速为5m/s、屋面坡度为34°的工况，得出屋面雪深分布云图，如图9所示，以验证物理分区方法是否合理。可以看出，屋面积雪分布十分复杂，同一分区内不同位置的侵蚀沉积程度差异较大，以屋脊为划分界限的物理分区方法难以反映其详细的分布规律。如图9的A区，积雪分布系数最小为0(屋脊处)，最大为0.9(屋檐处)，而经过计算可知A区整体积雪分布系数为 0.58，若以0.58作为设计参考值，在屋檐处会存在安全隐患，而在屋脊处则不经济，可见屋面物理分区方法并不可取。

图8 风向角及屋脊、屋面物理分区的规定

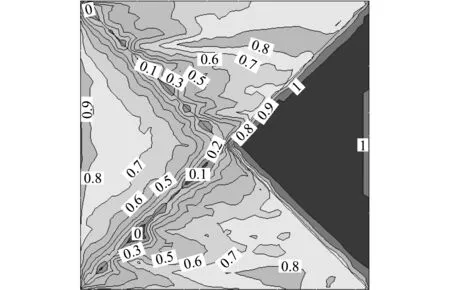
图9 物理分区下的屋面积雪分布

为探究沿屋面坡度方向和长度方向上的积雪分布规律，以及屋面角部和中部积雪的差异，依据图9的积雪分布规律，对攒尖四坡房屋进行更为细致的分区，如图10所示。

4.2 风向角对屋面积雪分布的影响

限于篇幅，仅给出风速为7 m/s、屋面坡度为34°时，不同风向角下的屋面积雪分布，如图11所示。可以看出，在0°风向角下，屋面积雪基本呈对称分布，迎风面和两侧面发生侵蚀，屋脊I和屋脊II附近的条状区域内完全侵蚀，背风面屋脊处和屋檐中部略有侵蚀，其余大部分区域无明显变化；在15°风向角下，D1～D6区完全侵蚀，B5区左上角发生沉积，积雪分布系数为1.1；在30°风向角下，B4与B5区交界处和B6区右下角发生沉积，积雪分布系数为1.1；在45°风向角下，屋面积雪基本呈对称分布，迎风面大部分完全侵蚀，仅A3，A4，D3和D4区余少量积雪，背风面一近似为三角形的区域发生沉积，积雪分布系数最大为1.2。

图12给出不同风向角下屋面各分区的积雪分布系数。可以看出，随着风向角由0°向45°转变，各分区积雪分布系数的变化没有固定规则，表现出的情况有一直增大、一直减小、先减后增或者先增后减，且风向角的变化对各屋面影响程度不一，A屋面和D屋面积雪分布系数变化幅度较小，而B屋面和C屋面有些分区变化幅度较大。对于A屋面，整体发生侵蚀现象，A1和A2区在不同风向角下积雪分布系数基本为0。对于B屋面，B2，B4，B5和B6区在0°和45°风向角下的积雪分布系数差值分别为0.82，0.85，0.83和0.78，变化幅度较大，值得注意的是，风向角由0°向45°变化过程中，B5和B6区由侵蚀状态逐渐转变为沉积状态。对于C屋面，C1和C3区随风向角变化幅度较大，其他区变化幅度较小。对于D屋面，各分区积雪分布系数变化趋势相似，基本表现为先减小后增大。

图10 屋面详细分区

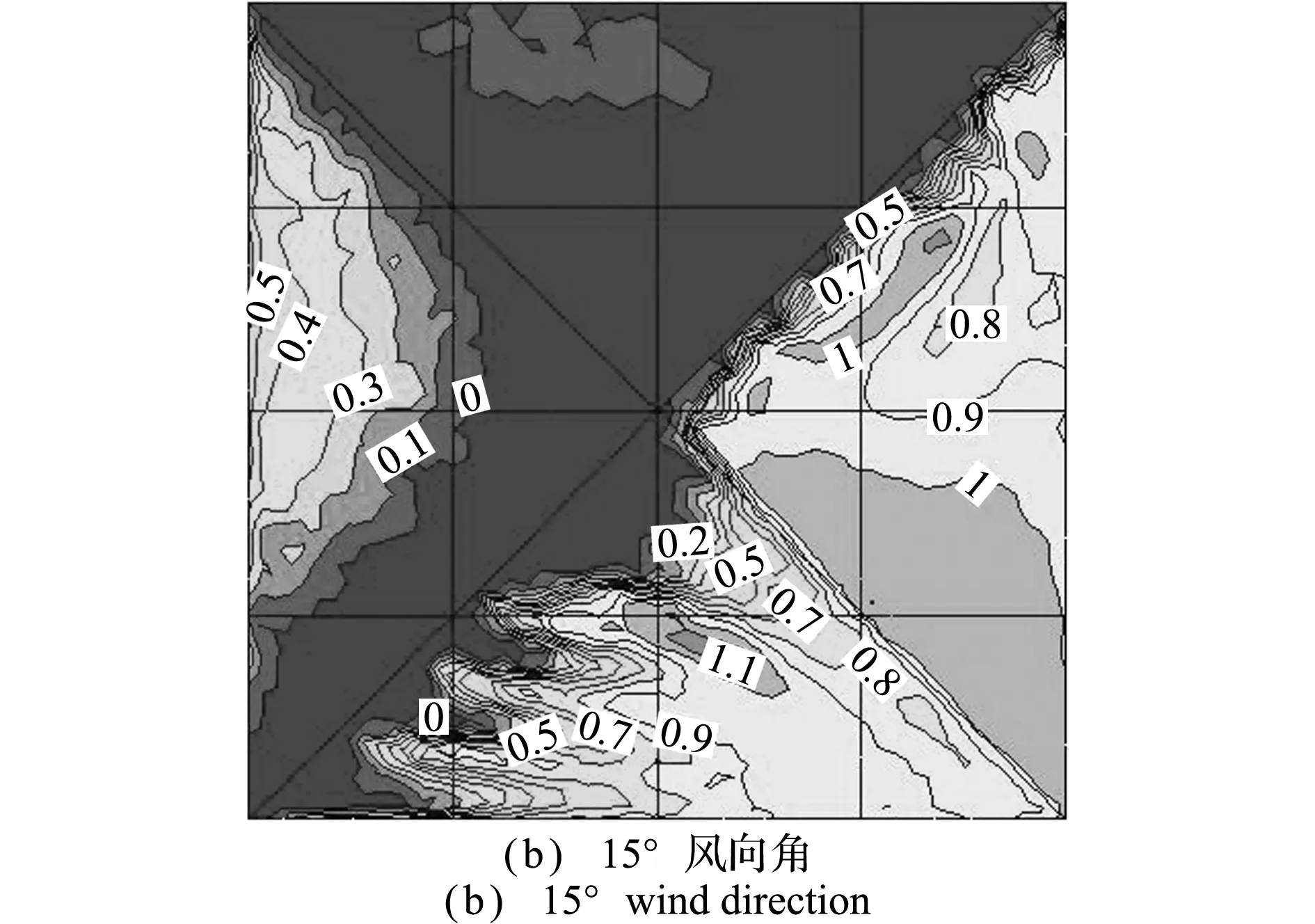
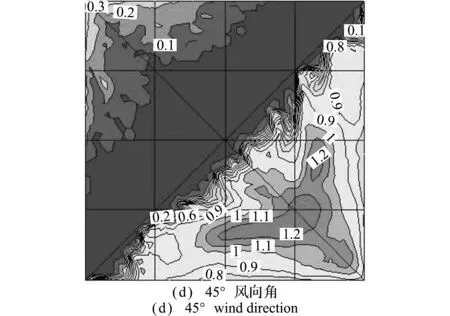
图11 不同风向角下的屋面积雪分布

图12 不同风向角下屋面各分区积雪分布系数

4.3 风速对屋面积雪分布的影响

图13给出45°风向角、屋面坡度34°情况下，风速由5 m/s递增至15 m/s时屋面积雪分布的变化情况。可以看出，不同风速下，屋面积雪基本沿屋脊I和屋脊III对称分布。随着风速的增大，迎风面侵蚀程度大幅增加直至积雪完全侵蚀，背风面大部分区域侵蚀量也增大，只有少数区域积雪量随风速变大而增多。风速为5 m/s时，除屋脊II和屋脊IV附近外积雪遍及整个屋面，迎风面积雪分布系数在0～ 0.8 之间；背风面屋脊附近发生侵蚀，其余大部分区域积雪没有明显变化。风速为7 m/s时，迎风面积雪分布系数在0～0.3之间，超过1/2的面积完全侵蚀；背风面在屋脊III附近发生沉积，积雪分布系数最大达到1.2。当风速为9 m/s时，迎风面整体完全侵蚀，背风面侵蚀程度进一步增大。当风速为11 m/s～15 m/s时，背风面总体雪量不断减少，完全侵蚀区域逐渐增多。

图13 不同风速下的屋面积雪分布

图14给出不同风速下，屋面各分区的积雪分布系数。可以看出，当风速为5 m/s时，各分区积雪分布系数均大于0，即积雪覆盖范围较大，几乎遍及整个屋面。当风速为7 m/s时，迎风面各区积雪分布系数明显降低，最大降低幅度可达0.6左右，A1，A2，A5和A6区积雪分布系数变为0；而背风面有个别区域积雪分布系数增大。当风速为 9 m/s 时，迎风面各分区积雪分布系数均为0，雪全部吹走，发生完全侵蚀。当风速由11 m/s增加至15 m/s时，曲线变化趋势相似，背风面各分区积雪分布系数逐渐减小。

图14 不同风速下屋面各分区积雪分布系数

4.4 屋面坡度对屋面积雪分布的影响

图15给出45°风向角、风速5 m/s情况下，屋面坡度分别为25°，30°，34°，40°和45°时屋面积雪的分布情况。可以看出，坡度越大屋面整体雪量越少，且不同坡度下屋面积雪均沿屋脊I和屋脊III对称分布。坡度为25°时，迎风面呈侵蚀状态，积雪分布系数在0～0.8之间；背风面超过一半区域发生沉积现象，最大积雪分布系数为1.3。坡度为30°时，迎风面侵蚀程度增大，背风面最大积雪分布系数减小至1.1。坡度为34°时，迎风面积雪分布系数进一步减小，在0～0.7之间，背风面未能观察到明显的沉积现象。坡度为40°～45°时，屋面发生明显的侵蚀现象，整体积雪分布系数在0.85以下。

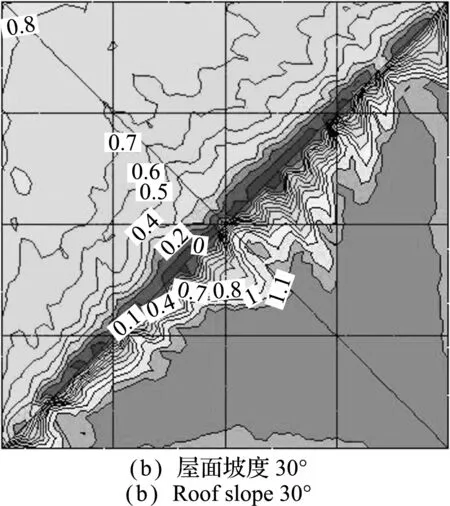
图15 不同屋面坡度下的屋面积雪分布

图16给出不同坡度下屋面各分区的积雪分布系数，可知大多数分区积雪分布系数随着屋面坡度的增加而减小。当坡度为25°～34°时，屋面上积雪分布系数最大的区域是B5，B6,C5和C6区，这四个分区位于背风面屋檐和角部，屋面上部发生漂移的雪容易在此处堆积；当坡度在40°～45°时，各分区积雪分布系数均小于1，即屋面整体呈侵蚀状态，此时屋面上积雪分布系数最大的区域变为B2和C2区，这是因为随着屋面坡度的增大，对气流阻挡作用增强，气流在屋脊II和屋脊IV处发生碰撞分离，一部分向上抬升，一部分在靠近屋脊处形成弯曲的循环气流，出现再附现象，这一涡流区称为回流空腔，该区域的静压低于大气压力，这里侵蚀程度小，所以雪量较多。

4.5 屋面积雪分布系数表

通过对4种风向角、6种风速以及5种屋面坡度条件下的攒尖四坡屋面风致雪漂移进行数值模拟，得到屋面各分区积雪分布系数值，取每个分区在120种工况下的最大值，即积雪分布系数包络值。由于攒尖四坡房屋的对称性，屋面上A1，A2，B1，B2，C1，C2，D1和D2区的雪荷载设计值应相等，其他区域同理，屋面最终分区如图17所示，得到表2的屋面各分区积雪分布系数，可供设计人员参考使用。由表2可知，在坡度较小时，屋面不同分区积雪分布系数有较大差异，最大差值为0.29，可知屋面分区的必要性。

图16 不同屋面坡度下屋面各分区积雪分布系数

图17 攒尖四坡屋面分区

表2 攒尖四坡屋面各分区积雪分布系数

5 结 论

(1) 对攒尖四坡房屋进行数值模拟时，计算域尺寸取30L×15L×10H(L为模型最大尺度，H为模型高度)，采取分区混合网格划分方式和k-kl-ω湍流模型，能较好地反映屋面的积雪分布规律。

(2) 对雪敏感的轻型屋盖，应考虑积雪分布的不均匀性进行分区，将每个屋面在平行屋檐方向二等分，在垂直屋檐方向按1∶2∶1的比例划分，共分为三个区，可以更详细地反映屋面侵蚀沉积规律。

(3) 屋面整体积雪量随风速增加呈减小趋势。当风速由5 m/s增加至7 m/s时，仅在背风面局部区域积雪量有所增加，迎风面整体及背风面大部分区域呈减小趋势，且迎风面对风速的增大更为敏感，其积雪分布系数发生骤降。当风速超过9 m/s时，迎风面积雪分布系数整体为0，呈完全侵蚀状态，背风面积雪分布系数不断降低。建议对此类房屋的风雪性能进行研究时，风速取5 m/s～9 m/s。

(4) 风向角的改变会使屋面积雪分布状态发生较大程度的变化，当风向角为0°和45°时屋面积雪基本呈对称分布。随着风向角由0°向45°转变，各分区积雪分布系数的变化没有统一规律，表现出的情况有递增、递减、先减后增或者先增后减，迎风面的侵蚀程度较背风面大。在特定条件下，某些分区会出现侵蚀状态和沉积状态的相互转化。

(5) 屋面坡度变化对屋面积雪分布状态有较大影响。当屋面坡度较大时，整体呈侵蚀状态；当屋面坡度较小时，迎风面仅发生侵蚀，背风面在部分工况下发生沉积。为方便工程设计人员参考使用，给出不同坡度屋面各分区的积雪分布系数，列入表2。