单双向流下浪流轮机空心翼径向屈曲失效分析

王世明， 葛 玲， 曹 宇， 贾巧娇

(1.上海海洋大学 工程学院，上海 201306；2.长崎大学 工学部，长崎 852-8043)

1 引 言

制造业的发展与环境的保护对开发清洁能源提出了强烈需求。丰富的海洋资源引起国内外广大研究学者和能源公司的重点关注。各种海洋能资源中，浪流能作为海洋清洁能源中的佼佼者，其开发获能率较高。因此，作为浪流轮机捕获海流能重要的部件，空心翼在复杂海洋环境下能否长期安全可靠运行至关重要。

国内外相关学者多年来一直致力于海洋能的利用开发研究，Saranyasoontorn等[1]采用逆向可靠性研究方法来估算600 kW三叶片水平轴风机的极限屈曲模型，结果表明，通过使用风况和短期最大响应等流入参数值为条件，通过简单的模型可以近似估算极端弯曲载荷。Tay等[2]采用元素失效方法对渐进性损伤进行建模和预测，将元素失效方法在Abaqus中编码为用户定义的UEL代码，将其模拟结果与实验数据进行了比较，结果表明，计算模型在极限载荷下能够映射复合结构中广泛的损伤模式。中国工程物理研究院采用弹塑性接触算法和自适应网格技术研究拉伸载荷下壳体的失效模式，研究表明，在环壳处的局部弯矩使壳体出现与塑性铰相似的屈服区，是导致失效的主导作用[3]。刘岗等[4]采用Metropolis算法，选取失效事件临界值和概率密度函数来研究风机叶片在不同风波动下的失效概率，试验结果表明，在该算法下，风机叶片的失效特征比传统的蒙特卡罗模拟法精度更高。目前国内外浪流能研究主要以改变翼型进行高效获能为主旨[5-10]。然而，对于失效研究常需要进行对应的破坏性实验进行验证，研究成本较高，鲜有具备该实验设备的重点实验室，故目前针对浪流轮机翼型的屈曲失效性评估的研究成果相对较少。

本文致力于预判浪流轮机早期屈曲失效为目标，考虑在浪流单双向作用力及主结构参数对空心翼径向应力和径向屈曲变形的影响，采用动量理论、屈曲失效理论及有限元模拟相结合的方法，对WTHB进行失效机理的分析，为同类型浪流轮机的设计参数提供参考建议。

2 建立模型

考虑到多因素混合非线性海流的研究难度和计算量，通过在轮机外部安装双向垂直浪流耦合导流筒，将复杂混合的浪流力简化为线性波作用力的组合，计算模型如图1所示。

此外，在浪流轮机运行过程中，还受到其他外部载荷作用力，如径向压力、法向力和有效推力。单向海流力为单独作用的弦向海流力F1，双向海流力为弦向与纵向海流力F1和F2两个方向冲击空心翼，海流力沿翼展方向与运动理论圆相切为有效推力Ft，海流力垂直于切向的分力为径向力Fn。双支持点分布位置表示为轮毂所在位置ξ与翼展L之比，其受力分析如图2所示。

图1 单双向浪流力

如图2所示，在低雷诺数下，有效推力Ft和径向力Fn为

(1)

(2)

利用有限元数值模拟中Static Structural与Eigenvalue Buckling两个模块进行联合求解，采用ANSYS/CFD进行内外网格划分，如图3所示，沿翼弦方向网格的疏密程度不同，网格从后缘以增长率1.6向主受力前缘表面加密，经网格无关性验证，该网格类型和设置符合要求，具体网格划分参数列入表2。

3 空心翼屈曲失效性判定

3.1 屈曲失效设计准则

3.1.1 Morison方程与非线性波浪力理论

一般而言，计算水下结构物所受波浪力可用Morison方程理论对其进行估算。对于本文研究对象处于浪流联合作用下的动态结构屈曲问题，基于非线性波浪力分析方法[11]，根据Morison 公式，可求得非常规海洋结构物海流力计算公式：

图2 空心翼受力

(3)

式中h为水下装置高度，d为水深，FI为垂直于主轴向上的惯性力，AI为流水质点方向主轴的投影面积，Cm为附加质量系数，FL为主轴单元高度上速度升力，AL为与流水质点垂直方向主轴的投影面积，CL为主轴横截面的速度力系数。

3.1.2 屈曲失效判断

采用动态非线性有限元分析软件模拟轮机的动态响应及失效。采用双线性弹塑性本构模型，动态屈服强度为[12-13]

(4)

式中σ0为静态屈服强度，Eh为应变硬化模量，εp为有效塑性应变，ε为等效塑性应变率，Dt和n为材料参数，取Dt=40.4 s-1，n=5。

考虑到失效损伤变量多，直接求解难度大，因此，对于叶翼屈曲失效的问题应用挪威船级社DNV《抗屈曲强度》来核算结构物整体屈曲失效[14]。由结构物的稳定性强度系数λ与临界值λ0进行比较，得到临界屈曲应力F0为

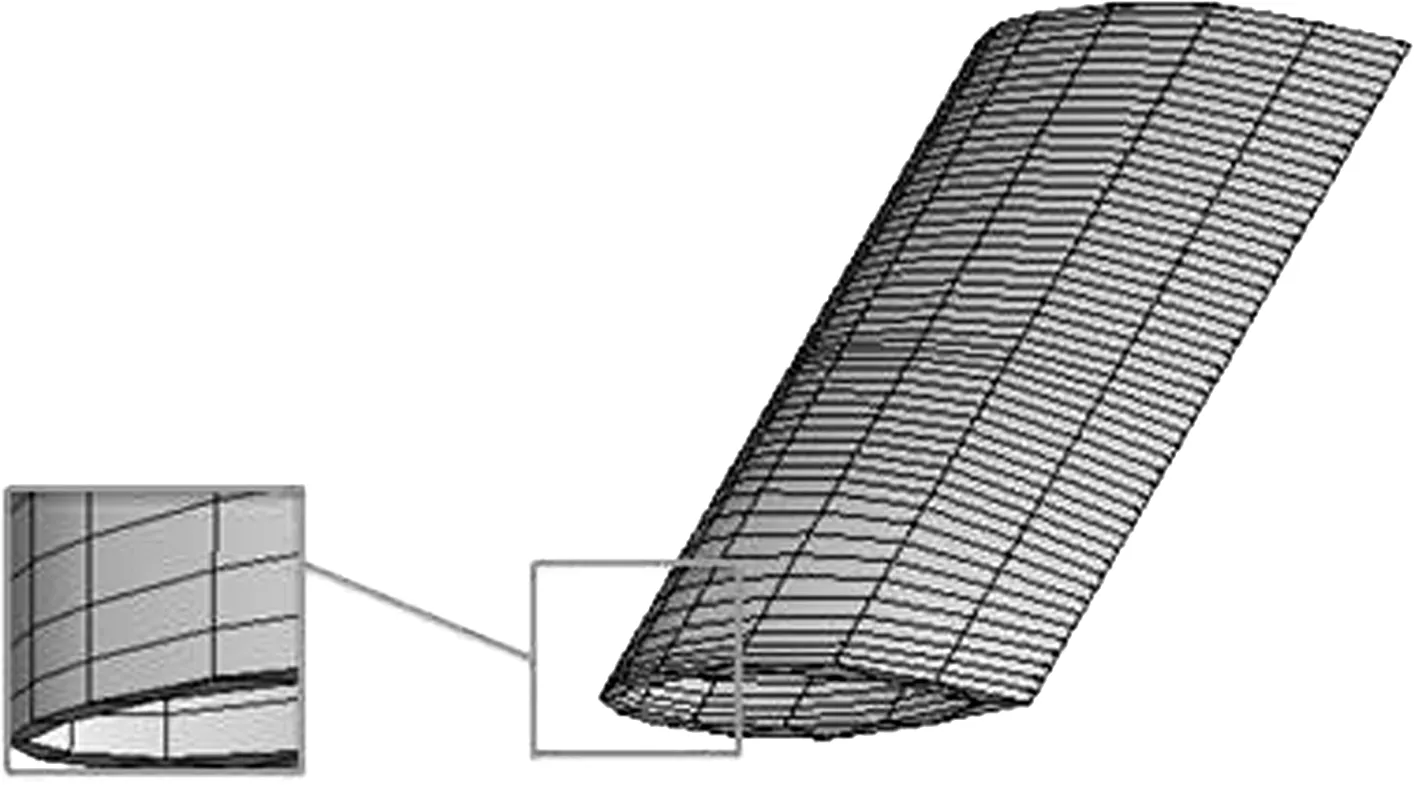
图3 空心翼有限元模型

表1 空心翼几何和材料设计参数Tab.1 Hollow blades geometry and material design parameters

表2 网格划分参数设置Tab.2 Meshing parameter settings

(5)

式中Fy为材料屈曲力，Fy=λ2σEA，其中，A为工作面积，σE为材料弹性屈曲应力。μ=0.5(λ-λ0)，外部浪流作用下，结构物受到的作用力超过F0时，可判定结构物发生屈曲。

3.1.3 屈曲变形判断

由里兹法[15]可知，屈曲变形为

(6)

式中x为自变量，ki为待定系数，[u0]为许用变形量，取[u0]=0.0025L，当满足不等式(6)时，结构物不发生屈曲。

3.2 失效性预判过程

叶翼不仅需要在复杂多变的海况下生存，还要持续有效地捕获海流能，在工程设计过程中，其屈曲失稳需要重点考虑，失效性的判定是一个多次验证的过程，如图4所示。

图4 装置失效性预测判定流程

4 参数分析

4.1 双向海流的径向压力和结构参数联合作用

4.1.1 水动力攻角对局部屈曲的影响

为考察水动力攻角对空心翼屈曲失效的影响，假定其他参数不变，设置两组工况，观察空心翼径向相对屈曲变形率。其中，工况1：α=20°，ξ/L=1/4；工况2：α=40°，ξ/L=1/4。

从图5可以看出，水动力攻角变化不改变空心翼整体屈曲特性，当水动力攻角为20°时，其屈曲变形率相对降低36.4%。因此，在极限浪流环境下，调节翼型至水动力攻角约20°，抗屈曲能力较佳。

4.1.2 双支撑点分布对局部屈曲的影响

为了考察双支撑点分布对空心翼屈曲失效的影响，进一步改变空心轴双支持点的分布位置并进行数值模拟，增加模拟工况3：ξ/L=1/6，α=20°和工况4：ξ/L=1/6，α=40°。并将计算结果与上述参数结果进行对比如图6所示。可以看出，随双支持点分布位置ξ/L从1/4变化至1/6，叶翼屈曲变形最值明显增大。

进一步如图7所示，由工况3空心翼的屈曲全过程形态可以看出，空心翼中部局部发生明显径向屈曲。上述分析结果表明，双支持点位置分布对空心翼屈曲影响大，控制双支持点在翼展侧均匀分布可以有效分担单位翼展截面积上的局部屈曲应力，有效降低结构屈曲幅值。

图5 径向相对屈曲变形率-翼展

图6 径向相对屈曲变形率-翼展

图7 在双向流作用下工况3空心翼屈曲全过程形态

4.2 单向海流的径向压力和结构参数联合作用

4.2.1 水动力攻角对局部屈曲的影响

对于单向海流力作用下水动力攻角对局部屈曲的影响，在相同工况下进行分析。如图8所示，当单向弦向海流作用时，空心翼沿中线相对屈曲率基本对称，中线和两端已处于塑性变形阶段，水动力攻角为40°时局部屈曲较大。

4.2.2 双支撑点分布对局部屈曲的影响

如图9所示，随着双支持点分布位置的改变，根据式(6)可知，uy与长度L呈反比，双支持点间的相对翼展ΔL越长，则屈曲变形uy越大。

为进一步讨论双支点分布对局部屈曲的影响，设置双支持点间的相对翼展变化量为ΔL，研究相对径向屈曲与翼展长的变化量的关系，如图10所示，随着翼展长的变化量ΔL的增大，相对径向屈曲增量曲线呈内凹递增，曲线斜率变大。

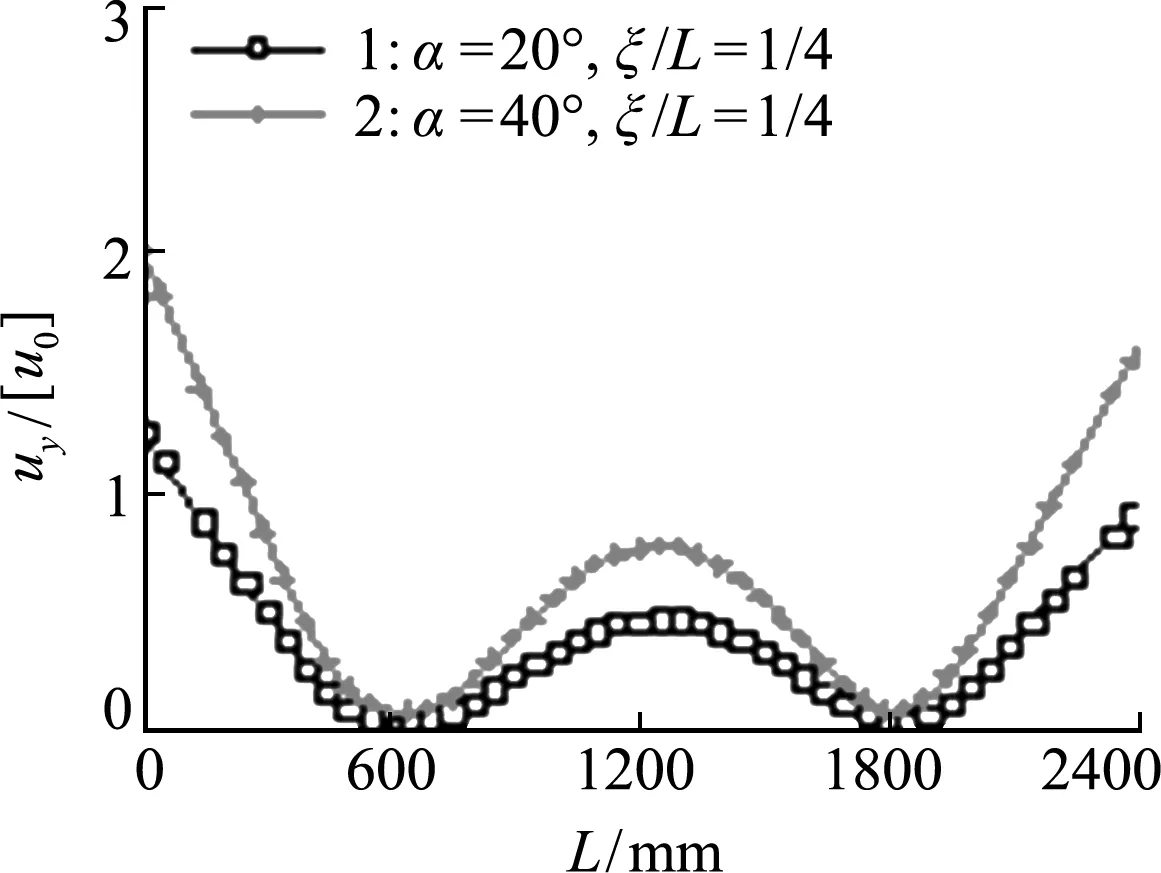
图8 径向相对屈曲变形率-翼展

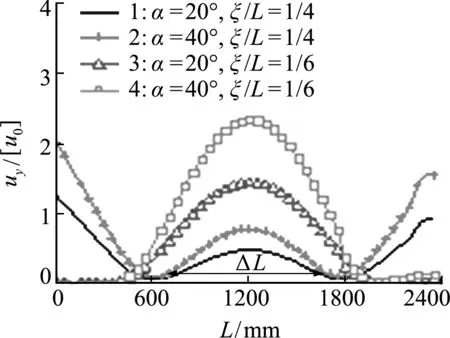
图9 径向相对屈曲变形率-翼展

图10 L =0处的相对径向屈曲-翼展长的变化量ΔL

5 结 论

(1) 水动力攻角和双支持点分布不改变空心翼相对屈曲特性。但双支持点分布对空心翼相对屈曲影响较大，且随着双支持点间的相对翼展变化量ΔL的增大，相对径向屈曲呈正相关。有效控制双支持点分布可以大幅降低结构屈曲最值。

(2) 水动力攻角为20°时，空心翼抗屈曲能力强，因此，同类型浪流轮机中，水动力攻角20°的轮机在易发生极限恶劣海况的流域下具有较强的生存优势。