防风网PM-IBM模型及其在堆场扬尘庇护区湍流模拟中的应用

许 栋， 张博曦， 及春宁， 杨海滔

(天津大学 水利工程仿真与安全国家重点实验室，天津 300072)

1 引 言

防风网是一种多孔墙式结构，能够降低网后局部风速，形成对颗粒扬尘的有效抑制，在港口堆场环境治理中广泛应用[1]。来流风在防风网上部形成绕流，与主流风速汇集形成高速风；下部由于阻风效应，网前高强度大尺度漩涡转化为低强度小尺度漩涡，大幅降低网后起尘量[2-4]，减风抑尘机理如图1所示。防风网风场研究方法主要有风洞实验及数值模拟，风洞实验可信度高，但实验周期长，设备制定复杂；随计算机技术发展，基于计算流体力学方法建立的计算机数值风洞得到广泛应用，王婷婷等[5]建立数值风洞研究数值边界精度，表明数值风洞能够有效模拟大气边界层；Scotta等[6]通过数值风洞研究桥梁所受风荷载，表明了数值风洞的可靠性。

防风网多孔结构数值模拟主要有3D实体建模及多孔介质PM模拟。3D实体建模方面，陈廷国等[7]针对防风网截面形式，通过贴体网格构建防风网模型，表明蝶形网的抑尘性能优于平面网；李建隆等[8]针对防风网开孔形状，通过混合贴体网格建立防风网模型，表明圆形开孔网的抑尘效果最佳；3D实体建模对开孔结构细节模拟更准确，但网格划分复杂，网格质量难以保证，建模耗时长。多孔介质方面，考虑防风网阻流效应实质为压降变化，引入多孔介质力学参数(渗透系数及惯性系数)实现压降变化，力学参数由网板风洞实验或刻画精细的CFD模拟取得[9]。Maruyama[10]结合多孔介质及大涡模拟对比风洞实验网后流场分布；许栋等[11]通过多孔介质模型探讨数值边界对计算精度的影响，表明多孔介质能够准确模拟防风网阻流效应；Teitel[12]采用Forchheimer压降方程模拟柔性开孔网，表明多孔介质力学参数受多因素影响。尽管多孔介质建模简便，但受防风网截面影响，前后压降关系复杂，针对防风网模拟的关键力学参数设定困难[11,12]；且多孔介质依赖网格边界，不同防风网形式及工程布置需要重新划分网格，建模效率低。

传统浸入边界法IBM将固壁边界离散为拉格朗日坐标下的IB点，在IB点处引入动量方程附加体积力，实现不可穿透固壁边界[9,13]。该方法能够快速构建物面边界，但要求防风网附近网格达孔径级别，网格数目大，如许栋等[9]采用浸入边界法对防风网模拟的计算网格总数约为2000万。

图1 防风网减风抑尘机理

本文结合多孔介质及浸入边界法，将压降以源项形式加入流体动量方程中，建立多孔介质-浸入边界模型(PM-IBM模型，下同)，实现边界的部分穿透性，结合通用计算流体力学求解器，为防风网截面选型和布置优化等工程应用提供高效建模工具；并探讨不同湍流模型下PM-IBM模型的计算精度，分析网高及开孔率对减风抑尘效果的影响。

2 数学模型建立

2.1 基于浸入边界法的风场控制方程

近地层空气受风速和温度等因素产生的密度相对改变率小于1%[14]，可视为不可压缩粘性流体。浸入边界法在不可压缩粘性流体N-S方程中引入附加体积力，流体控制方程为

(1)

(2)

(3)

式中u为速度矢量,p为压强,t为时间,Re为雷诺数,f为附加体积力矢量,为梯度算子,rhs(x,tn)为对流项、粘性项及压力梯度在tn时刻之和,V(Xi,tn + 1)为可移动固体边界期望速度。本文采用四点正则插值函数，形式为

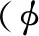
(4)

(5)

(6)

(7)

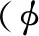
2.2 防风网PM-IBM模型

防风网PM-IBM模型核心是根据网后压降确定风场控制方程中的附加体积力大小。防风网两侧压降与来流雷诺数Re相关，即

Re=ud/υ

(8)

式中u为风速，υ为空气运动粘滞系数，d为柔性网线直径或刚性网孔间距。

Re<10时，防风网风阻效应可按多孔介质渗流处理，适用达西定律，故网两侧压降见式(9)。Re>10时，受孔隙惯性效应影响，形成非达西流动，压降由Forchheimer方程[8]求解，见式(10)；当Re>450时，K0趋近于0[18]；当Re>250时，惯性系数β仅为开孔率α的函数，A1(Re)为常数，约为 0.52[19]。故Re>450时，压降由式(10)简化为式(11)。

(9)

(10)

(11)

综上，当来流风垂直于防风网时，不考虑法向力源，则IB点流向力源及IB点附近网格的附加体积力计算形式为

(12)

(13)

2.3 PM-IBM模型软件实现

FLUENT是应用最广的通用CFD软件之一。模型采用FLUENT用户自定义函数(UDF)通过3个功能模块实现PM-IBM模型，如图2所示，各模块功能如下。

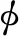
(2) DEFINE_ADJUST。将欧拉网格流场信息插值到IB点并计算IB点附加体积力。

(3) DEFINE_SOURCE。利用式(13)计算网格附加体积力并嵌入动量方程中。

通过3个模块，IBM方法能够在流体方程中实现多孔介质，形成PM-IBM模型。利用该模型，不需要再引入另外的多孔介质模型及防风网边界条件，该边界条件由PM-IBM的散点(Immersed Boundary Points)代替。该方法同传统多孔介质相比，无需绘制物面边界，对于不同形状边界只需导入相应的边界散点坐标，对复杂几何边界条件的适应能力强。

图2 基于FLUENT的PM-IBM模型实现

3 模型验证

选用张宁[20]的风洞实验进行模型验证。试验段长为6.75 m，宽为0.72 m，高为0.6 m，防风网高H0为0.03 m，开孔率为38.5%。实验布置如 图3 所示。

数值风洞涉及大量网格计算，覆盖整个实验区域，计算量大，考虑区别于实验，数值风洞能够通过入流边界和底部粗糙度快速形成稳定大气边界层[5,11]，故选取网前10H0、网后30H0、高10H0的范围作为计算域，能避免边界对计算结果的影响[3,21]；防风网采用PM-IBM模型，计算域左侧为速度入口边界(Velocity inlet)，右侧为自由出流边界(Outflow)，上部为对称边界(Symmetry)，下部为不可滑移固壁边界(Wall)，各边界条件数学表达见式(14～17)。网格采用正交结构网格，近网区局部加密，总网格数为69000，计算域及网格划分如图4所示。

入口边界ux=f1(x,z)，uz=f2(x,z)

(14)

(15)

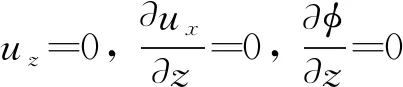
(16)

固壁边界ux=uz=0

(17)

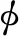
图3 实验布置模型[20]

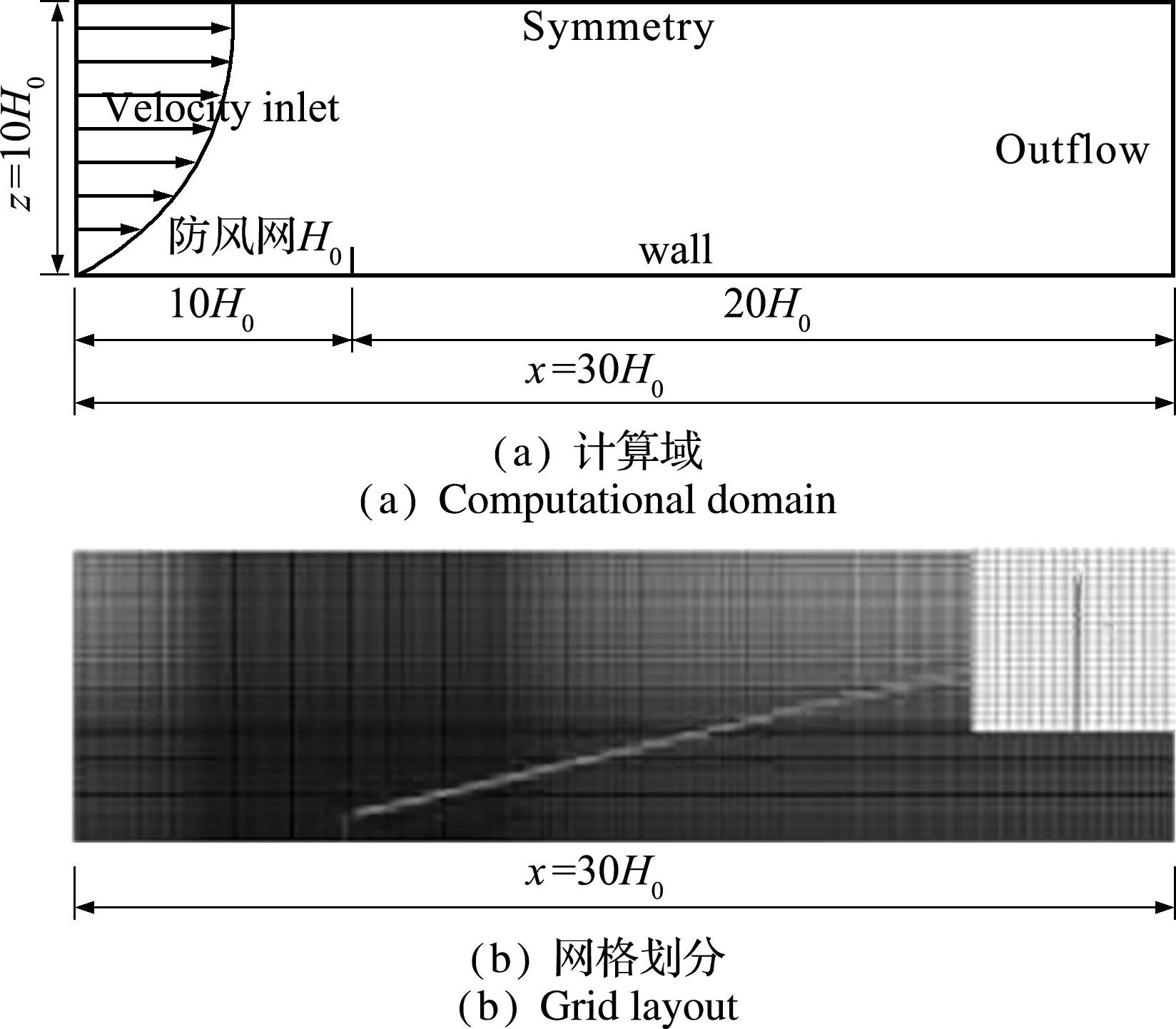
图4 计算域和网格划分

入流边界速度分布采用对数律拟合为

uz=(u*/κ)ln(z/z0)

(18)

式中uz为高度z处的平均风速，u*为地表摩擦风速，κ=0.41为冯卡门常数，z0为空气动力学地表粗糙度。根据实验数据[20]，u*和z0由已知不同高度的风速值求得，

z0=exp[(u1lnz2-u2lnz1)/(u1-u2)]

(19)

u*=u1κ/[ln(z1/z0)]

(20)

式中z1和z2为高度，u1和u2为高度z1和z2处平均测量风速，κ为冯卡门常数，z0为空气动力学地表粗糙度。数值模拟入口速度分布与实验稳定风速对比如图5所示，数值模拟风速分布精度高，近底区误差在1%以内，说明数值风洞能够为防风网提供与物理风洞相近的来流边界。

图5 入口断面风速分布验证

基于PM-IBM模型，分别采用Standard模型、RNG模型和Realizable模型对防风网进行数值模拟，同传统多孔介质模型(流体采用Realizable模型)及实验数据进行对比，网后距离为2H0，4H0，6H0和8H0处的水平风速如图6所示。网后上部高速条带区除Standardk-ε模型外均与风洞实验较吻合，误差在2%以内，Santiago等[22]研究表明，RNGk-ε模型和Realizablek-ε模型能够准确模拟网后上部高速条带区，与本文结论一致。近网区底部数值模拟同实验有所差异，其中Realizablek-ε模型断面风速分布同实验误差最小，偏差范围2.6%～4.1%；RNGk-ε模型近网近底区存在回流。PM-IBM模型同传统多孔介质模型对比，近网区域流速基本一致，网后6H～8H范围PM-IBM模型近底(0H～0.5H)流速略优于多孔介质模型。PM-IBM模型总体精度能够有效模拟防风网阻风效应。

4 计算结果及分析

根据模型验证结果，基于PM-IBM模型采用Realizablek-ε模型研究开孔率及防风网高度影响。

4.1 开孔率的影响

开孔率α是影响防风网遮蔽效应的关键因素，本文对20%～45%开孔率防风网空气动力学特性进行数值模拟，计算域如图4所示，网后流速分布如图7所示，可以看出，网后存在明显风速较低区域；20%～30%开孔率网后5～7倍网高存在回流现象，易引起颗粒起扬；开孔率>35%时，回流区基本消失。此外，随开孔率增大，防风网阻风效应减弱，风速增大。

定义无量纲剩余风速uz/Uz为网后风速与入流断面等高处的风速比，不同高度剩余风速沿程分布见图8。可以看出，高度z≥0.6H0范围，剩余风速沿程呈先减后增趋势；高度z≤0.4H0范围，受局部回流影响，20%～25%开孔率剩余风速沿程于5倍网高附近存在局部增加现象，抑尘效益降低。最小剩余风速随开孔率增大而增大，20%开孔率减风效果最优，该结果同Lee等[23]以双顿粒子测速技术所得20%开孔率防风网对网后顺流向速度折减最大的结论一致。综合剩余风速及网后回流因素，建议最优防风网开孔率为30%～35%，最优庇护区在z≤0.8H0和x= 2H0～8H0范围内，此区域剩余风速不超过0.3，抑尘效益高。

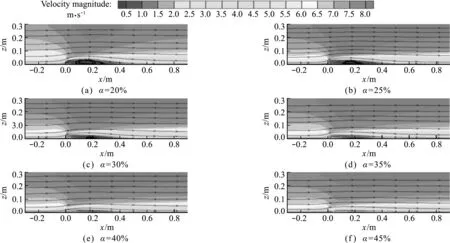
图7 不同开孔率风速分布

图8 剩余风速沿程变化

4.2 防风网高度的影响

网高是影响庇护区的重要结构因素之一，本文设置网高H=H0，1.2H0，1.4H0，1.6H0和1.8H0和未设防风网情况，其中初始堆场高度H0=0.03 m，开孔率为35%。堆场前端距防风网2H0，计算域及边界条件设置如图9所示，堆场采用不可穿透浸入边界施加，防风网采用PM-IBM模型。

图9 堆场布置及边界条件

堆场附近风场结构如图10所示，有网工况网与迎风面间形成低风速区，减风效果明显；无网工况迎风面及堆顶风速较大，抑尘效益低。受堆场自身遮蔽效应影响，来流风被迫抬升，背风面均存在风速较低回流区。

不同网高堆场表面速度垂向分布如图11所示，堆场表面高度2H范围内，有网风速明显小于无网工况，迎风面风速最大减小约65%，堆顶及背风面最大减小约55%。对堆顶，H<1.4H0时，堆场表面风速随网高增加线性减小；H≥ 1.4H0时，网高与风速变化的线性关系趋于平缓；对背风面，网高增加对表面风速影响趋于0；对迎风面，表面风速随网高增加逐渐减小。考虑防风网建设成本，建议防风网高度为堆场高度的1.4倍。

图10 近堆场风场结构(H=H0)

图11 不同网高风速垂向分布

5 结 论

本文首次将多孔介质与浸入边界法相结合，提出了能准确、快速模拟防风网边界的PM-IBM模型，避免了对开孔边界的直接描述，使网格数量大幅降低，在保证计算精度和计算效率前提下，实现结构化网格下防风网的高效数值建模，结果如下。

(1) PM-IBM模型能够有效模拟防风网的阻风效应，其中Realizablek-ε模型模拟最为准确。

(2) 防风网最优开孔率为30%～35%，网后最优庇护区在高度<0.8H,沿程2H～8H之间。

(3) 当网高小于堆场高1.4倍时，堆顶风速随网高增大近似线性降低；当网高大于堆场高1.4倍时，风速降低幅度趋于平缓。