四角点支承四边自由矩形薄板屈曲问题的新解析解

杨雨诗， 安东琦， 倪卓凡， 李 锐

(大连理工大学 工业装备结构分析国家重点实验室，大连 116024)

1 引 言

角点支承的矩形薄板作为一种常见结构形式，广泛应用于建筑结构、机械构件和航空航天器等工程实际。板的屈曲作为典型的力学失效形式之一，在过去几十年受到了广泛关注，该类问题的解析求解在理论与实际中都具有重要意义。对于板的线性屈曲问题，核心是在给定的边界条件下，通过求解高阶偏微分控制方程，得到对结构设计具有重要参考价值的屈曲载荷和相应的屈曲模态。然而，由于数学上的复杂性，许多问题难以得到同时满足高阶偏微分方程和边界条件的解析解。现有的矩形板的屈曲解析解主要局限于两对边简支的情况，即Lévy型板，而对于角点支承条件下的非对边简支的矩形板，绝大部分研究都是基于有限差分法[1]、微分求积法[2]、离散奇异卷积法[3,4]、无网格法[5]和广义伽辽金法[6]等近似/数值方法，而关于解析方法和解析解的报道较少。

钟万勰院士[7-9]将辛数学思想引入弹性力学中，为弹性力学求解开辟了新思路，由此产生的辛弹性力学方法已在结构皱褶[10]、断裂[11]和弹性波[12]等众多领域中得到了充分的应用。在辛弹性力学的基础上，李锐等[13-17]针对复杂板壳力学问题提出了一种新的解析方法，即辛叠加方法，获得了若干板壳结构弯曲、振动和屈曲问题的新解析解。辛叠加方法的基本思想是将待解决的问题转化为几个可由辛数学法求解的子问题的叠加。该方法的求解过程是在基于辛空间的哈密顿体系中进行，而不是在传统的基于欧几里德空间的拉格朗日体系中进行；解析解是通过直接的严格推导得到，不需要对解的形式做任何假定，这是经典的半逆方法难以做到的；同时，该方法规避了单纯采用辛数学方法出现的本征方程难以解析求解等瓶颈，在解析求解含有复杂边界的板壳振动和屈曲问题中具有独特优势。

本文首次采用辛叠加方法解析求解四角点支承四边自由矩形薄板的屈曲问题——由于边界条件的复杂性，此类问题是各类边界条件下矩形薄板问题中最难求解的情况之一。给出了不同长宽比和不同载荷比情况下四角点支承四边自由矩形薄板屈曲问题的算例，结果表明，无论是屈曲载荷还是相应的屈曲模态，本文方法得到的结果均与精细有限元分析结果吻合很好，从而证明了本文方法以及所得解析解的正确性。

2 矩形薄板屈曲问题的Hamilton体系控制方程与本征问题

利用Hellinger-Reissner两类变量的变分原理，并结合拉格朗日乘子法[18]，在区域Ω内可以由变分原理(1)描述薄板的屈曲问题[19]，

(1)

通过对独立变量w，θ，T和My进行变分，由δΠH=0可得

(2)

式(2)可表示为

(3)

(4)

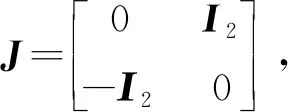
(5，6)

(7)

展开得

(8)

解得

λ1，2=±a1i,λ3，4=±a2i

(9)

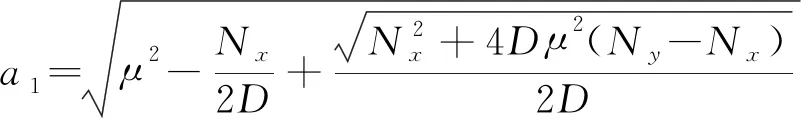
由式(9)得式(6)的w(x)的本征解为

w(x)=Acos(a1x)+Bsin(a1x)+

Ccos(a2x)+Fsin(a2x)

(10)

式中A，B，C和F为常数。

3 四角点支承四边自由矩形薄板屈曲问题的辛叠加解析解

为求解四角点支承四边自由薄板的屈曲问题(原问题)，需要通过辛方法先求解出基本子问题的解析解，再通过叠加法寻求原问题的解析解。图1为辛叠加图解，坐标系的原点位于板的一角，板的长度为a，宽度为b，坐标轴ox和oy分别与板的左边和上边重合，如图1(a)所示。原问题可以转化为两个子问题的叠加，分别如图1(b，c)所示，其中P为角点支承，F表示自由，S表示简支。

图1 辛叠加

原问题的边界条件为在四个角点上满足点支承条件，即

w|(0,0), (0,b),(a,0),(a,b)=0

(11)

在四条边上，满足自由边界条件，即

Vy|y =0,b=0,My|y = 0,b=0

Vx|x = 0,a=0,Mx|x = 0,a=0

(12)

两个子问题中板的初始边界条件均为四边简支，满足边界条件：

w|y = 0,b=0,My|y = 0,b=0

w|x = 0,a=0,Mx|x = 0,a=0

(13)

先以图1(b)表示的子问题(1)为例进行求解。对于x=0和x=a边简支的矩形薄板，其在该两边的边界条件要求：

w(x)|x = 0,a=w″(x)|x = 0,a=0

(14)

将式(10)代入式(14)，板发生屈曲要求常数A,B,C和F不全为0，即要求式(14)方程组存在非零解，因此要求上述方程组的系数矩阵行列式为0，即可得

sin(aa1)sin(aa2)=0

(15)

其根为

a1,2=±mπ/a

(16)

式中m=1,2,3,…。于是可以解得本征值为

(17)

本征向量为

(18)

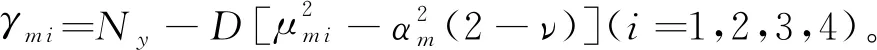
(19)

式中Cm i(m=1,2,3,…;i=1,2,3,4)为待定常数，可以根据y方向的边界条件确定。原问题拆分成子问题后，需在子问题(1)的y方向强加位移，对应的边界条件为

(20)

将式(19)代入式(20)，即可确定子问题(1)的模态位移表达式为

(21)

对于图1(c)表示的子问题(2)，求解过程与子问题(1)类似，对应的板的模态位移为

(22)

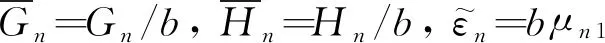
通过上述推导，得到了两个子问题的模态位移解，其他各物理量，如弯矩和转角等都可以相应地导出。待定参数Em,Fm,Gn和Hn需根据子问题的叠加与原问题的等价性确定。根据四角点支承四边自由矩形薄板的边界条件，要求四个角点上的位移为0，子问题叠加后，无论待定参数Em,Fm,Gn和Hn取何值，角点位移为0的条件均已满足；要求沿y=0,y=b,x=0和x=a四条自由边，均满足弯矩和等效剪力为0。子问题叠加后，弯矩为0的条件已经满足，只需再满足等效剪力边界条件即可。

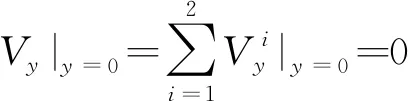
(23)

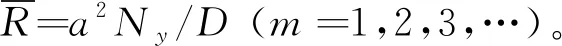
(24)

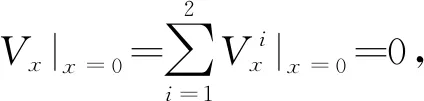
(25)

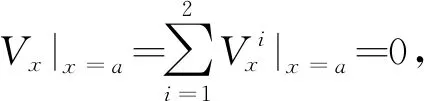
(26)

式(23～26)为无穷联立方程，实际取有限项，如取m=1,2,3,…,nt,n=1,2,3,…,nt。板发生屈曲要求待定系数Em,Fm,Gn和Hn不全为0，即要求式(23～26)组成的联立方程存在非零解，因此要求上述方程组的系数矩阵行列式为0，从而给出关于屈曲载荷的方程，求解即得到屈曲载荷解。确定屈曲载荷后，即可得到上述方程组的非零解，一并代回式(21,22)并求和，即得到对应的屈曲模态。

4 算 例

表1和表2给出了四角点支承四边自由矩形薄板屈曲载荷的收敛性结果。结果表明，对于当前问题，只需取nt=35,即可使所有计算结果均收敛到五位有效数字的精度，因此在实际计算中取nt=35。表3和表4分别给出了长宽比为1和2的四角点支承四边自由矩形薄板的屈曲载荷，其中载荷比从0至5取整数，泊松比取0.3。通过与精细有限元分析(采用ABAQUS软件中S4R单元，单元尺寸0.005a)获得的收敛结果对比可见，所有当前结果均与有限元结果吻合得很好。表5给出了b/a=1,Nx/Ny=1时四角点支承四边自由矩形薄板的前十阶屈曲模态，对比发现，辛叠加方法也能精确求出屈曲模态。上述算例充分证实了本文求解方法的正确性和所得解析结果的精确性。

表1 b/a=1,Nx/Ny=0时板的前十阶屈曲载荷收敛性结果Tab.1 Convergence study for the first ten buckling the plates under Nx/Ny=0,with b/a=1

表2 b/a=2,Nx/Ny=5时板的前十阶屈曲载荷收敛性结果Tab.2 Convergence study for the first ten buckling the plates under Nx/Ny=5,with b/a=2

表3 b/a=1时不同Nx/Ny下板的前十阶屈曲载荷Tab.3 First ten buckling the plates under different Nx/Ny,with b/a=1

表4 b/a=2时不同Nx/Ny下板的前十阶屈曲载荷Tab.4 First ten buckling the plates under different Nx/Ny,with b/a=2

表5 b/a=1,Nx/Ny=1时板的前十阶屈曲模态Tab.5 First ten buckling mode shapes of the plates under Nx/Ny=1 and b/a=1

5 结 论

本文采用辛叠加方法得到了单向和双向面内载荷作用下,四角点支承四边自由矩形薄板屈曲问题的新解析解。给出了不同长宽比和不同载荷比情况下板的屈曲载荷和屈曲模态的综合结果，可为其他各类近似/数值方法提供对比和检验的基准。由于辛叠加方法对解的形式不做任何假定，自始至终都是严格的解析推导，因此有望进一步推广，得到更多复杂板壳问题的新解析解。