基于物理中面FGM板屈曲的有限元分析

孙 云， 陈 江， 李世荣

(扬州大学 建筑科学与工程学院，扬州 225127)

1 引 言

功能梯度材料FGM作为一种新型的复合材料，其材料性能在空间连续变化，有效地缓解了应力集中。FGM在航空航天、建筑、机械和电子等工程领域有着广泛的应用前景。

已有很多文献分别基于经典板理论、一阶剪切变形板理论和高阶剪切变形板理论等对FGM板的屈曲问题进行了研究。基于经典板理论，Javaheri等[1]用能量法研究了四边简支FGM板在双向面内压力下的屈曲行为。Shariat等[2]得到了有初始几何缺陷的四边简支FGM板在双向面内压力作用下临界荷载的闭合解。Yu等[3]用Levy法求得了弹性地基上两对边简支另两对边为任意边界的FGM板在单向和双向受压时发生屈曲的解析解。Mohammadi等[4]基于最小势能原理建立了FGM薄板屈曲的控制方程，用Levy法得到了两对边简支FGM板的临界荷载。Asemi等[5]用三维有限元分析方法研究了FGM板在各种面内荷载作用下的屈曲，其解既能保证位移的连续性也能保证应力和应变的连续性。

基于一阶剪切变形板理论，Yang等[6]用一阶摄动法分析了矩形板的弹性屈曲问题。Zhao等[7]采用无网格 kp -Ritz 法对FGM板在热机荷载下的屈曲进行了分析。Naderi等[8]用最小势能原理对FGM板的屈曲构形进行了分析。Mohammadi等[9]基于Mindlin板理论，用Levy法分析了两对边简支其他边界任意的矩形板的屈曲问题，得到了不同荷载条件下板的临界屈曲荷载。Nguyen-Xuan等[10]基于边的光滑有限元方法对FGM Mindlin板进行了静力分析、自由振动分析和屈曲分析。

基于三阶剪切变形板理论，Reddy[11]对FGM板进行了分析研究，得到了四边简支板的静力响应、屈曲和自由振动的Navier解。Bodaghi等[12]基于高阶剪切变形板理论，用Levy法分析了两对边简支另两对边为任意边界的FGM板在各种荷载条件下的屈曲问题，得到了临界荷载的解析解。Thai等[13]采用精化板理论对FGM板的屈曲进行了分析，得到了四边简支FGM矩形板在双向面内受压时临界荷载的闭合解。Zenkour等[14]基于精化的高阶剪切和法向变形板理论，用Navier法研究了简支FGM矩形板在单向压力和双向压力作用下的屈曲行为。Singh等[15]基于非多项式高阶剪切变形理论，用Navier法研究了简支FGM板在均匀、线性和非线性荷载作用下的屈曲响应。在上述研究方法中，解析法如Navier法和Levy法仅能考虑有限的几种边界条件，而有限元法可以研究边界条件、荷载工况、材料组成和几何尺寸为任意情况时的问题。

上述文献中，FGM板的控制方程是基于几何中面建立的。张大光[16]提出了物理中面的概念，基于物理中面建立FGM板的控制方程可消除拉弯耦合的影响，简化方程的求解，在保证计算精度的同时提高了计算效率。但目前基于物理中面研究的文章较少，Zhang等[17]基于物理中面和经典板理论分析了FGM矩形薄板的弯曲、振动、屈曲和非线性弯曲；Latifi等[18]基于物理中面和经典板理论，采用Fourier级数展开法研究了任意边界条件下FGM矩形薄板在双向受压时的屈曲问题。

本文将基于物理中面和经典板理论研究FGM板的屈曲问题。首先，根据最小势能原理建立FGM板有限元形式的屈曲控制方程；然后，利用FGM板的屈曲方程与参考均匀板屈曲方程之间的相似性，建立FGM板的临界荷载与参考均匀板的临界荷载之间的相似转换关系式；最后，通过数值算例，将临界荷载的有限元解与转换关系式求得的临界荷载进行比较，并讨论边界条件、荷载工况、材料梯度指数和长宽比等对FGM板临界荷载的影响。利用转换关系，只要知道参考均匀板的临界荷载即可求解出FGM板的临界荷载，这种方法极大地减少了计算工作量，为FGM材料的推广起积极的推动作用。

2 基于物理中面FGM薄板的基本方程

考虑FGM矩形板，长度为l1，宽度为l2，厚度为h，将xOy面置于板的几何中面上，x轴和y轴分别沿板的长度和宽度方向，z轴沿厚度方向向上。设FGM板的弹性模量E只沿厚度方向按幂函数规律变化，

(1)

式中Et和Eb分别为板上下表面组分材料的弹性模量，n为材料梯度指数，n∈[0,∞)，当n=0和n→∞时，FGM板分别退化为由上下表面材料组成的均匀板。

取FGM板的物理中面为z=z0所在平面[16]，其中

(2)

基于物理中面的概念，经典板理论下FGM板内的位移场为

(3)

式中u，v和w分别为板内任意一点在x，y和z方向的位移。

根据几何方程[17]，可得板内的应变为

{ε}=(z-z0){κ}

(4)

式中 {ε}=[εx,εy,γx y]T

根据胡克定律[17]，板内的应力与应变关系为

{σ}=[D]{ε}

(5)

式中 {σ}=[σx,σy,τx y]T,[D]为弹性矩阵，即

(6)

由于FGM板的泊松比ν变化不大，假设其为常数。

3 FGM薄板屈曲的有限元分析

对FGM板进行有限元分析时，采用4结点矩形单元，单元平面尺寸为2a×2b，每个结点有3个自由度，即挠度w、绕x轴的转角θx和绕y轴的转角θy。根据直法线假设，每个结点的位移可表示为

(i=1,2,3,4) (7)

则每个单元有12个自由度，单元的结点位移列阵可以表示为

{d}(e)=[{d1}(e),{d2}(e),{d3}(e),{d4}(e)]T

(8)

将单元内任一点的挠度w表示为含12个待定系数的多项式

w=α1+α2x+α3y+α4x2+α5xy+α6y2+α7x3+

α8x2y+α9xy2+α10y3+α11x3y+α12xy3

(9)

将单元的4个结点坐标(xi,yi)(i=1,2,3,4)代入式(9)的挠度w及其导数∂w/∂y和∂w/∂x的表达式，可得到12个以α1～α12为变量的线性方程组，解此方程组得α1～α12，再将其代回式(9)可得到单元内挠度的表达式为

w=[N]{d}(e)

(10)

式中 [N]=[[N1][N2][N3][N4]]为形函数矩阵，[Ni]=[Ni,Ni x,Ni y](i=1,2,3,4)，

(i=1,2,3,4) (11)

(12)

将式(10)代入式(4)，可得用单元结点位移表示的单元应变

{ε}(e)=[B]{d}(e)

(13)

式中 [B]=[[B1][B2][B3][B4]]为应变矩阵，其中子矩阵

(i=1,2,3,4) (14)

将式(13)代入式(5)，可得用单元结点位移表示的单元应力

{σ}(e)=[D][B]{d}(e)

(15)

平面线弹性问题的最小势能原理为

δΠ=δ(U+V)=0

(16)

式中U为应变能，V为外力势能。

整个结构的应变能可表示为

(17)

式中ne为单元总数。

将式(13)的单元应变和式(15)的单元应力代入式(17)，得

(18)

式中 [k](e)=∬A(e)[B]T[D*][B]dxdy为单元刚度矩阵，

(19)

整个结构的外力势能可表示为

(20)

(21)

式中 [k0](e)=∬A(e)[B0]T[N0][B0]dA为单元的初应力刚度矩阵。

(22)

将式(18,21)的单元结点位移列阵扩展为结构的整体结点位移列阵{d}，并将单元的刚度矩阵进行相应的扩展和组装，再代入式(16)，考虑δ{d}T的任意性，可得

([K]-λ[K0]){d}=0

(23)

式中 [K]为整体刚度矩阵，[K0]为整体的初应力刚度矩阵，{d}为整体结点位移列阵。

令式(23)的系数行列式等于0，得到FGM板的屈曲控制方程

|[K]-λ[K0]|=0

(24)

该方程的最小特征值即为FGM板屈曲时的临界荷载。

4 FGM板与参考均匀板临界荷载之间的相似转换关系

将式(1)代入式(2)，并进行积分计算得

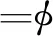
(25)

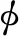
将式(1)代入式(19)，并利用式(25)得

D′=Db/c

(26)

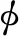
将式(26)代入式(18)的单元刚度矩阵[k](e)

[k](e)=[kb](e)/c

(27)

式中 [kb](e)为由下表面材料组成的均匀板的单元刚度矩阵。

式(27)组装后得结构的整体刚度矩阵为

[K]=[Kb]/c

(28)

将式(28)代入式(24)可得

|[Kb]/c-λ[K0]|=0

(29)

特殊情况下，当n→∞时，FGM板退化为由下表面材料组成的均匀板，此时有

|[Kb]-λb[K0]|=0

(30)

对比式(29，30)，可得FGM板的临界荷载λ与参考均匀板(由下表面材料组成)的临界荷载λb之间的相似转换关系为

λ=λb/c

(31)

因此，若已知参考均匀板的临界荷载λb，就可由式(31)直接计算出FGM板的临界荷载λ，极大地减少了计算工作量。

5 数值结果与讨论

FGM板由Al2O3/Al组成，上表面材料为纯陶瓷(Al2O3)，下表面材料为纯金属(Al)。Al2O3和Al的弹性模量分别为Et=380 GPa和Eb=70 GPa。FGM板的泊松比取为ν=0.3。

考虑如图1所示的四种边界情况,(1) 四边简支(SSSS), (2) 两对边简支两对边固支(SSCC), (3) 四边固支(CCCC), (4) 两对边简支两对边自由(SSFF)。

在x=0和x=l1边上，

简支时,w=0，∂2w/∂x2+ν(∂2w/∂y2)=0

固支时,w=0， ∂w/∂x=0

在y=0和y=l2边上，

简支时,w=0， ∂2w/∂y2+ν(∂2w/∂x2)=0

固支时,w=0， ∂w/∂y=0

考虑三种荷载工况，其相应的薄膜力和荷载参数λ分别为

(1) 单向受压时,(Nx,Ny,Nx y)=Px(-1,0,0)

(2) 双向受压时,

(3) 周边剪切荷载时,(Nx,Ny,Nx y)=Px y(0,0,1)

5.1 有限元解

通过MATLAB软件编写有限元程序对FGM板的临界荷载进行计算。首先，进行收敛性分析。考虑四边简支(SSSS)的方板，假设板的两对边

图1 四种边界条件

表3为单向受压时，不同边界条件和材料梯度指数情况下FGM方板的临界荷载。可以看出，在给定边界条件下，临界荷载随着材料梯度指数的增加而减小；材料梯度指数一定时，边界约束越强，临界荷载越大。

表1 单向受压时SSSS方板的无量纲临界荷载pc r

表2 周边剪切荷载作用下SSSS矩形板的无量纲临界荷载pc r

表3 单向受压时FGM方板的临界荷载Pc r(l1=l2=1 m,h =0.01 m)

图2为单向受压时，不同边界条件下FGM矩形板的临界荷载随长宽比的变化曲线。可以看出，在CCCC，SSCC和SSSS边界条件下，临界荷载呈波浪形变化，最终趋于平缓；在SSFF边界条件下，临界荷载呈单调递减并趋于平缓。

表4给出了双向受压时，不同边界条件和长宽比情况下FGM矩形板的临界荷载。可以看出，在SSCC边界条件下，随着长宽比的增加，临界荷载略有突变；而在其他三种边界条件下，临界荷载均单调递减。

图3给出了不同荷载工况下，SSCC边界条件FGM方板的临界荷载随着材料梯度指数变化的曲线。可以看出，周边剪切荷载作用下，临界荷载最大，其次是单向受压时，双向受压时的临界荷载最小；当n较小时，临界荷载随着材料梯度指数急剧下降，当n较大时，临界荷载下降较平缓。

5.2 由转换关系得到的解

由式(31)可知，若已知参考均匀板的临界荷载，就可由FGM板的临界荷载与参考均匀板临界荷载之间的相似转换关系直接计算出FGM矩形板的临界荷载。表5为单向受压时，三种边界条件下由转换关系得到的FGM板的临界荷载，并与本文的有限元解和文献[4]的结果进行了比较。由 表5 可知，转换关系得到的结果与有限元解和文献结果吻合得非常好，验证了相似转换关系的存在及其正确性。

图2 单向受压时FGM矩形板的临界荷载随长宽比的变化关系(n =1,l2=1 m,h =0.01 m)

表4 双向受压时FGM矩形板的临界荷载Pc r(n =1,l2=1 m,h =0.01 m)

图3 SSCC边界条件FGM方板的临界荷载随材料梯度指数的变化关系(l1=l2=1 m,h=0.01 m)

表5 单向受压时由转换关系得到的FGM矩形板的临界荷载Pc r(n =1,l2=1 m,h =0.01 m)

6 结 论

基于经典板理论，引入物理中面概念，利用最小势能原理推导了FGM板屈曲的有限元控制方程。利用FGM板的屈曲方程与参考均匀板屈曲方程之间的相似性，得到了FGM板的临界荷载与参考均匀板的临界荷载之间的相似转换关系，从而将FGM板临界荷载的计算转变为参考均匀板的临界荷载及其材料不均匀系数的计算。通过数值算例，分析了边界条件、荷载工况、材料梯度指数和长宽比等对FGM板临界荷载的影响，得到以下结论。随着材料梯度指数的增加即金属组分的增加，FGM板的临界荷载减小；边界约束条件越强，临界荷载越大；随着板的长宽比的增加，临界荷载总体趋势是减小的，但单向受压和双向受压时SSCC边界条件FGM板的临界荷载略有突变；周边剪切荷载作用下的临界荷载最大，单向受压时次之，双向受压时最小。