中国银行系统的宏观审慎监管研究
2020-10-24高倩倩
高倩倩,范 宏
(东华大学 旭日工商管理学院,上海 200051)
0 引言
近年来金融危机的爆发对银行系统产生了深刻的影响,引发了国内外学者和相关监管机构对银行系统监管的重视。金融危机表明仅仅以关注单个银行稳健性为核心的微观审慎监管存在一定的监管缺陷。微观审慎监管是从单个银行的视角考虑,即使单个银行本身是稳健的,也可能会通过银行间的同业拆借联系发生传染风险,从而危害整个银行系统。因此,基于整个银行系统视角的宏观审慎监管已经成为国内外学者以及相关监管机构的共识。由于整个银行系统是由多个银行通过同业拆借市场相联系的银行网络系统,因此银行系统的宏观审慎监管即为监管由各个银行相互联系的银行网络系统。目前对中国银行网络系统进行动态建模并进行宏观审慎监管的研究未见。因而,本文研究中国银行网络系统定量的宏观审慎监管方法。
目前对银行系统的宏观审慎监管的研究相对较少,已有研究中Balogh[1]、Cihak等[2]、李健全[3]、何德旭等[4]以及范小云和王道平[5]主要是对宏观审慎监管进行定性分析。其中,国外学者Balogh[1]总结了金融稳定委员会、国际货币基金组织和国际清算银行已经确定的几个常用的宏观审慎工具。Cihak等[2]通过定性分析全球金融危机背景下监管措施的变化特征,发现监管的变化是缓慢渐进的,变化的领域主要在银行资本化、多样化、审计和存款保险等方面。国内学者李健全[3]对微观审慎监管和宏观审慎监管进行了定性总结,指出两者监管目标一致,只是监管的角度、方法有所不同。何德旭等[4]指出从长期来看有必要建立我国金融业的宏观审慎监管体系。范小云和王道平[5]定性总结了全球金融监管框架—巴塞尔Ⅰ和巴塞尔Ⅱ与巴塞尔Ⅲ的区别和联系。
一些学者仅定量的分析了银行的系统性风险,未涉及对宏观审慎监管的定量研究。如:Lehar[6]使用Merton框架模型,在考虑了资产相关性的基础上测量了不同国家银行的系统性风险。Elsinger等[7]构建了包含不确定性因素的银行同业拆借的网络模型,并定义了清算支付向量来处理银行在违约情况下的债务支付,探讨了澳大利亚银行的系统性风险。高志勇[8]采用资本资产定价模型(CAPM)测算18家美国银行的风险波动率和系统性风险。指出金融监管目标框架应该以控制系统性风险为中心。此外,迟国泰等[9]使用KMV模型实证测算出我国上市银行的违约概率与我国债券市场所接受的上市银行违约概率最为接近,且国有上市银行违约概率最低。
还有些学者,如Berger和Bouwman[10]、Gauthier等[11]、Liao等[12]、Karmakar[13]、García-Palacios等[14]以及Zhou[15]围绕对银行系统实施资本要求,探讨其监管效果。其中Berger和Bouwman[10]研究美国银行系统中资本如何影响银行绩效,发现在任何时候资本都有助于提高小银行的生存率和市场占有率。Gauthier等[11]以及Liao等[12]分别以加拿大银行系统和荷兰银行系统为研究样本,通过构造同业拆借网络模型以及网络清算算法来衡量银行的系统性风险,并使用不同的风险分配机制来获得每个银行的宏观审慎资本。研究表明对银行系统实施宏观审慎资本极大的促进了金融稳定。Karmakar[13]通过构建包含银行、企业和储户的动态随机一般均衡模型来研究在偶然绑定资本要求约束下的宏观审慎监管对银行金融决策的影响。研究发现更高的资本要求可以抑制商业周期波动并提高福利。相反,García-Palacios等[14]引入银行系统中固有的道德风险问题,通过建立效用函数以及比较分析,发现增加资本要求并不总是最优的政策。类似的,Zhou[15]通过构建金融机构风险承担行为的静态模型,求解未监管系统中(即无资本要求)以及监管系统中(即带有资本要求)的效应最大化问题。发现施加资本金要求虽然可以降低单个机构的风险,但它同时也增强了系统性联系。
通过对已有研究的回顾,发现当前对银行系统的宏观审慎监管研究是发展趋向,而国内目前的相关研究都为定性分析,因而,本文的特色在于对银行系统进行了动态建模,并收集中国上市银行的实际数据,使用金融仿真计算的方法对中国银行系统展开了定量的宏观审慎监管研究。在对银行系统进行动态建模的过程中,国外有少量的宏观审慎监管的定量研究,但还不够完善。如Lehar[6]和Elsinger等[7]主要研究银行的系统性风险还未涉及对银行系统的宏观审慎监管研究,前者构建的模型主要考虑了银行资产的相关性影响未考虑银行同业拆借的网络结构;后者考虑了银行同业拆借的网络,但该模型演化的周期只有两步,并且网络上银行的资产负债只是随机产生,并没有随时间动态变化。Gauthier等[11]和Liao等[12]开始研究对银行系统的宏观审慎监管,但是也没有考虑银行间同业拆借的网络结构的影响。因此,本文首先基于Lehar[6]和Elsinger等[7]测量银行系统性风险的模型建立了动态的中国银行网络系统模型,该模型的改进之处在于:第一,考虑了银行同业拆借的网络,并且该拆借网络在银行系统的演化过程中是动态变化的;第二,网络上各银行的资本和负债在每个时间步也是动态变化的。然后,基于以上动态的中国银行网络系统模型,利用Gauthier等[11]和Liao等[12]中Component VaR(简称为“CVaR”) 、Incremental VaR(简称为“IVaR”) 、Shapley value EL以及ΔCoVaR的四种风险分配机制的原理,并通过编写算法及仿真计算,展开对中国银行网络系统定量的宏观审慎监管研究。最后依据仿真结果对中国银行系统的宏观审慎监管进行分析和总结,为我国相关监管机构提供一定的理论依据。
1 中国银行网络系统模型及定量宏观审慎监管模型
本文构建的中国银行网络系统模型框架如图1(a)所示,首先利用中国2008年至2015年16家上市银行的实际拆借总数据,通过标准化和最优化估计中国银行系统的同业拆借矩阵,该矩阵即为中国银行网络系统的网络结构(数学模型见1.1节);然后利用中国银行系统的实际股价数据估计网络中各银行的资产的动态演化,再利用中国银行系统的实际初始负债数据估计各银行的负债的动态演化;最后随着网络结构的演化及网络节点上银行的资产和负债的演化,形成了中国银行网络系统的动态演化(数学模型见1.2节)。

图1 中国银行网络系统模型及定量宏观审慎监管模型框架
图1(b)为定量宏观审慎监管模型。该模型建立在中国银行网络系统的动态演化的基础上,即在银行系统网络结构的演化和银行资产负债演化的基础上,首先计算网络中各银行的损失,然后引入四种风险分配机制,计算各银行的宏观审慎资本,从而进一步对中国银行网络系统进行宏观审慎监管(数学模型见1.3节)。
1.1 估计银行系统的网络结构
由于银行部分信息的非透明化,无法获取银行间具体的拆借数据,只能从银行的资产负债表中获得银行的拆借总资产ai和拆借总负债bi。因此,使用研究中普遍使用的通过最小化银行拆借信息的不确定性的方法来估计银行间的同业拆借矩阵。银行间的同业拆借关系可以用矩阵X(N×N)来表示:

(1)
公式(1)中,矩阵中元素xij表示银行i向银行j的借款;每行元素之和bi表示银行i的拆借总负债;每列元素之和aj表示银行j的拆借总资产。具体表示为:
(2)

(3)
(4)
1.2 资产负债表的动态演化
由于银行资产的价值并不是每天都能观测到的,但是可以从股市获取银行股价每天的数据,因此,可以用银行股价的时间序列数据通过随机模型和最大似然估计法来估计银行资产每天的价值,得到资产价值的动态演变。因而,本文假设银行i的总资产Vi服从于几何布朗运动,用公式(5)来表示:
dVi=uiVidt+σiVidz
(5)
公式(5)中,μi和σi分别表示银行i资产的漂移率和波动率;dz是一个维纳过程,即银行的总资产V的演变是一个随着其漂移率波动的随机游走且不可预测的几何布朗运动随机微分方程。
根据期权定价模型,通过银行的资产组合和无风险利率下的负债,银行i在t时刻的股权价值可以用公式(6)[16]来表示:
(6)
其中φ(·)为标准正态分布函数;
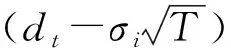
LDi(t)=LDi(0)ert
(7)
dt用公式(8)来表示:
(8)
上式中T表示365天。


(9)

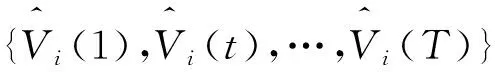
在计算出漂移率μi和波动率σi值后,最终依据公式(10)得到银行资产的演化值Vi(t):
(10)
其中,z服从于标准正态分布。
银行网络系统中的总负债Di(t)用公式(11)来表示:
Di(t)=(Vi(0)-Ci(0))ert
(11)
其中,Ci(0)=7%*Vi(0),Ci(0)表示银行i的初始资本。根据《巴塞尔协议III》中对全球各商业银行的核心一级资本充足率提升至7%的相关规定,这里定义银行的初始资本即为7%的初始总资产。
当银行i自身由于资不抵债而破产即满足公式(12)时,就判定银行i倒闭:
Vi(t)+ai(t)-Di(t)-bi(t)<0
(12)
公式(12)中,银行i的拆借资产ai(t)和拆借负债bi(t)会受到银行间同业拆借的传染性风险的影响,在此对Elsinger等[7]所提出的清算支付机制进行改进,以确定动态演化的银行系统中受到同业拆借传染下的债务支付。先定义一个新的矩阵Π∈[0,1]N×N来对银行的同业间负债进行标准化处理,具体表示为:
(13)


(14)
其中,ei(t)=Vi(t)-Di(t)
(15)
这里使用Elsinger等[7]的违约机制算法求解p*(t)。需要注意的是,当银行i倒闭时它对其债务银行的支付是有限的,设置支付比例为:
(16)
因此,受到银行间同业拆借联系的影响,银行i的倒闭对其债务银行j的总资产和总负债产生影响,按照公式(17)进行更新:
Vj(t+1:T)=Vj(t)-χi*xij
Dj(t+1:T)=Dj(t)-χi*xij
(17)
公式(17)中,在t时刻,由于银行i的倒闭,受银行系统拆借网络的影响,银行i的债务银行-银行j,其总资产Vi和总负债Dj在t+1到T时刻都发生了变化,分别为银行j在t时刻的总资产Vj(t)、总负债Dj(t)与倒闭银行i有限的债务支付之差。
同时,银行i倒闭后将其清除出银行网络系统并设置其拆借关系xi,j(t)=0,再重新估算拆借矩阵,因此在t+1时刻银行j的拆借总资产和拆借总负债更新为公式(18):

(18)
经过以上银行资产负债表及其拆借关系的演化过程,我们能够得到动态的银行网络系统。
1.3 定量的宏观审慎监管方法
量化银行的宏观审慎资本C的核心在于动态的量化银行的损失,在每次的仿真过程中,银行的总资产和总负债以及拆借资产和拆借负债经过t个时间步的动态演化后,银行的损失用公式(19)来设定:
(19)
其中ei(t)用上节中的公式(15)来计算。
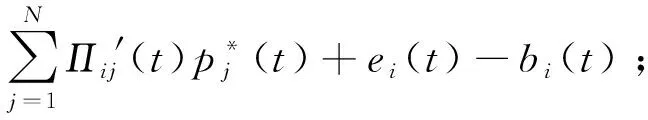

(20)

银行的倒闭概率设定为银行的倒闭次数与仿真总次数m之比。对银行系统定量的宏观审慎监管的算法流程图如图2所示。
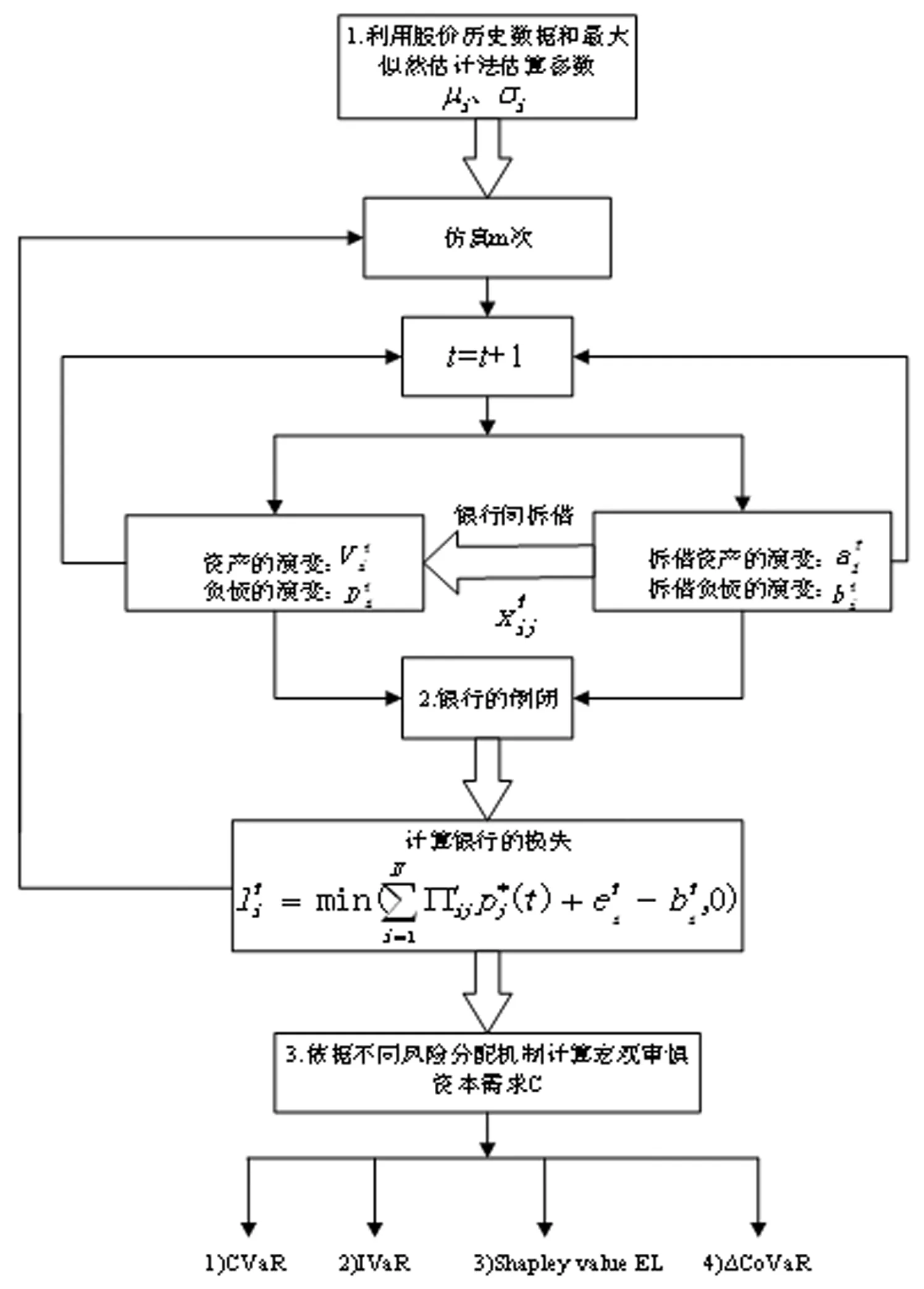
图2 定量的宏观审慎监管的算法流程
1.3.1 四种风险分配机制
参考Gauthier等[11]和Liao等[12],我们使用以下四种风险分配机制来量化每个银行的宏观审慎资本:ComponentVaR、IncrementalVaR、Shapley value EL以及ΔCoVaR。银行的宏观审慎资本在每种风险分配机制下的量化方法如下:
(1)ComponentVaR
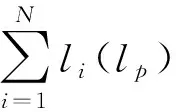
在ComponentVaR(CVaR)计算机制下银行i的宏观审慎资本为:
(21)

(2)IncrementVaR
该机制的核心思想是依据银行系统中某个银行的增加所引起的风险的增加来重新分配资本。即该机制所衡量的是银行系统中某个银行的破产违约为整个系统所带来的风险贡献。
具体计算是在test次的仿真中将银行系统的总损失从大到小排列,设定置信水平为99.5%。在此情况下得到所有银行的总损失以及去除银行i之后的总损失分别为VaRp和VaR-i。因此,银行i增加的风险为:IVaRi=VaRp-VaR-i。
在IncrementVaR(IVaR)计算机制下银行i的宏观审慎资本为:
(22)
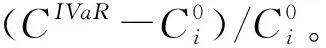
(3)Shapley value EL
该机制即为在IVaR机制的基础上仿真n次,求算数平均。对VaRp和VaR-i进行算数平均之后求出的新的IVaRi表示为φi。即该机制所衡量的是某个银行的违约破产对银行系统风险的平均边际贡献。
在Shapley value EL计算机制下银行i的宏观审慎资本要求为:
(23)

(4)ΔCoVaR
银行i的CoVaR是银行i的损失取特定条件下的VaR值时相应的银行系统的总损失CoVaRi[18]为:
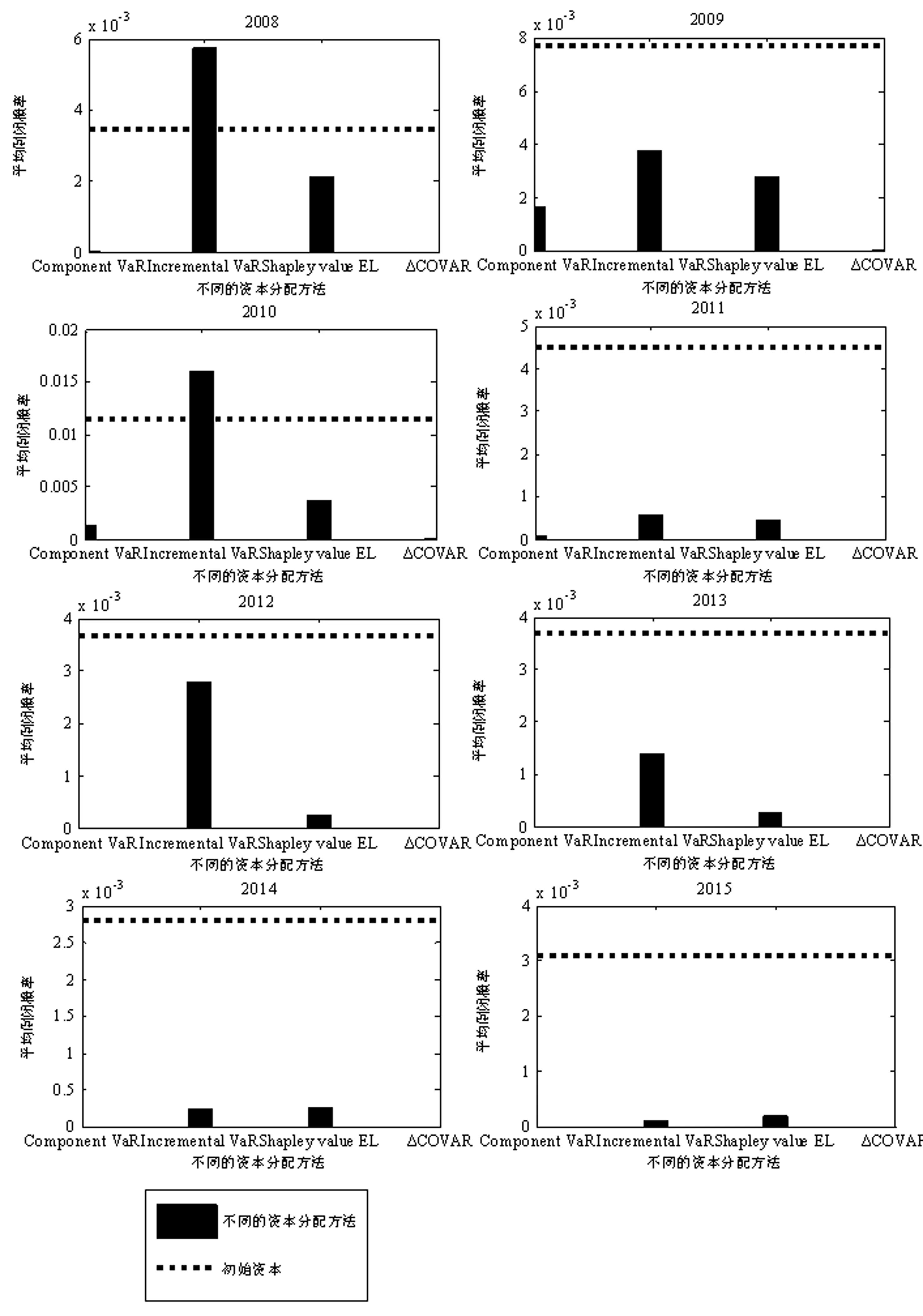
Pr(1p λ=0.1 (24) ΔCoVaRi是CoVaRi与银行i的损失取其中位数的条件下银行系统总损失的VaR值之差: ΔCoVaRi=CoVaRi-(VaRp|1i=median(1i)) (25) 在ΔCoVaR计算机制下银行i的宏观审慎资本为: (26) 本文收集了中国2008年至2015年16家上市银行的资产负债表数据及其股价的相关交易数据。其中,银行的资产负债表的数据中主要用到银行的总资产(V)、总负债(LD)以及银行同业间拆借总资产(a)和银行同业间拆借总负债(b),这些数据主要用于银行网络模型中的初始化设置以及银行间拆借矩阵的初始估计。需要注意的是,农业银行和光大银行都是在2010年上市,因此,在2008年至2010年,银行系统中仿真的银行数BN=14,2011年至2015年BN=16;银行的初始资本C0参考巴塞尔协议,设置C0为7%的总资产的初始值。以银行在m=10000次仿真中的倒闭概率来衡量银行的稳定性。 使用以上四种风险分配机制,通过仿真计算获得每个银行的宏观审慎资本,然后对银行系统进行宏观审慎监管,探讨银行的倒闭情况以及监管效果。 2.2.1 资本的变化 图3是各银行每年在四种风险分配机制下的宏观审慎资本与系统中的初始资本相比的变化率。图3表明,ΔCoVaR和ComponentVaR风险分配机制下银行的宏观审慎资本的变化情况类似,都表现出大多数银行的宏观审慎资本呈现出正向增加,表明了大多数银行当前的资本是不足以抵御其风险的;少数银行的资本则呈小幅度降低,表明了少数银行当前的资本是较为充足的,因此在经过重新分配后,资本有所减少。相比之下,ΔCoVaR下的宏观审慎资本的增加稍大于ComponentVaR。其中宁波银行和南京银行每年增加的较多,也表明了这两个银行对系统性风险的贡献最大。此外,平安银行、华夏银行、光大银行以及北京银行在这两种风险分配机制下的宏观审慎资本也呈现出相对明显的增加,而中国银行、农业银行、交通银行、建设银行以及工商银行则出现小幅的降低。除以上银行外,其他银行的变化不明显,在初始资本值附近轻微浮动。IncrementalVaR机制下,除了2008、2010以及2012年的宁波银行、2009、2012以及2013年的南京银行和2010年的平安银行的宏观审慎资本出现相对明显的小幅降低,其他银行每年都保持小幅的增加。而Shapley value EL机制下各银行的宏观审慎资本每年总体上变化不大。 图3 不同机制下各银行每年的资本变化率 2.2.2 宏观审慎资本下银行的倒闭概率 利用四种风险分配机制下的宏观审慎资本仿真计算银行的倒闭概率,得到图4所示的仿真结果。图4表明,银行的资本在初始值的情况下,2008年至2015年期间,中国银行、交通银行、建设银行和工商银行都未发生倒闭,表明了其较强的稳健性;而宁波银行、南京银行、华夏银行和北京银行则每年都发生倒闭并在2010年倒闭概率最高,除了2015年,平安银行也每年都发生倒闭且倒闭概率也较高。总体来看,银行系统在2008年至2010年期间最不稳定,在2012年和2014年则相对较为稳定。在银行系统中的资本通过四种风险分配机制被重新计算情况下,由图4可知在Component VaR、Shapley value EL以及ΔCoVaR三种分配机制下,除了ComponentVaR机制在2009年使招商银行的倒闭概率明显增加以及Shapley value EL机制在2008年使宁波银行和南京银行的倒闭概率轻微增加之外,2008年至2015年期间每个银行的倒闭概率都有所降低。IncrementalVaR机制使每个银行的倒闭概率在2011年、2014年和2015年都明显降低,而在其他年份则使个别银行的倒闭概率增加。其中包括2008年、2010年及2012年的宁波银行、2009年、2010年、2012年及2013年的南京银行、2008年的民生银行以及2010年的平安银行。整体而言,ComponentVaR机制和ΔCoVaR机制的监管效果较为显著,都使银行的倒闭概率降低较多。相比之下,在2008年至2011年期间ΔCoVaR机制最为显著,而2011年之后两者无区别。Incremental VaR 机制和Shapley value EL机制的监管效果没有以上两机制的效果显著,且前者对个别银行体现出明显的反向监管效果。 图4 不同机制下每年各银行的倒闭概率 将图3和图4相结合进行分析,探讨倒闭银行在以上四种风险分配机制下倒闭概率降低的内在机理。研究发现,银行的资本在通过四种风险分配机制的再分配过程中,本质上是将资本从稳定性较高、资本相对充足的大银行(如:中国银行、工商银行、交通银行、建设银行及农业银行等)转移到了资本不足的小银行,尤其是宁波银行和南京银行,分配后资本增加的幅度较大,使其倒闭概率降低,因而提升了小银行抵御风险的能力。然而,在特定年份下的少数银行经宏观审慎监管后的倒闭概率反而增加。究其原因,发现这些银行在初始资本下已经倒闭,且调整后其资本也有所降低,这表明了这些银行的风险较大,即使使用以上三种风险分配机制进行资本的再分配也不能满足其资本需求。这也表明了以上三种风险分配机制的局限性,并不能保证每次都能将稳健性较强的银行的资本转移到相对较弱的银行。 图5 不同机制下银行系统每年的平均倒闭概率 虽然ComponentVaR机制、IncrementalVaR机制和Shapley value EL机制这三种风险分配机制使个别情况下一些银行的倒闭概率增加,但以银行系统的平均倒闭概率来衡量,由图5可知,除了2008年和2010年的IncrementalVaR机制之外,2008年至2015年四种风险分配机制下银行系统的平均倒闭概率与初始资本下的相比,都有所降低。这充分表明了四种风险分配机制下的宏观审慎资本对银行系统的显著监管效果。相比之下,ΔCoVaR机制的宏观审慎监管效果最好,IncrementalVaR机制则最差。 经过以上的分析,为了探讨影响银行宏观审慎资本的因素,选定银行的总资产、同业拆借总资产以及同业拆借总负债展开相关性分析。 表1 宏观审慎资本与银行特性之间的相关性 由表1可知,2008年至2015年每年在Incremental VaR机制和Shapley value EL机制下银行的宏观审慎资本都与其总资产之间呈较强的正相关。即规模越大的银行相应的需持有较多的资本,该结论也与支持了大型银行若违约,将通过同业银行间的拆借联系对银行系统产生重大影响,因此需要持有更多的资本。Component VaR机制体现了两者之间的具有一定的相关性,但是没有Incremental VaR机制和Shapley value EL机制下的相关性显著。而ΔCoVaR机制下则表明两者之间为弱相关,其相关性不明显不足以说明问题。由于ΔCoVaR风险分配机制与银行损失的分布有关,而中国银行系统中各银行的规模异质性较强,银行间的拆借也由于各银行自身的状况而不同,因此,银行的损失分布没有一定的规律可循,就使得该机制下的宏观审慎资本与银行特性不相关。总体来看,四种风险分配机制下的宏观审慎资本与银行的同业间资产和同业间负债之间的相关性并不明显,表明了在本文同业银行间的拆借网络为全连接的仿真情景下,银行的倒闭是以其“资不抵债”引发的基础倒闭为主导,而由银行间的拆借造成的传染倒闭则较少,因此,银行的同业间资产与负债和宏观审慎资本的相关性不大。 本文利用中国上市银行银行的实际资产负债表中的相关数据,通过构建动态的中国银行系统网络模型并编写Component VaR、Increment VaR、Shapley value EL以及ΔCoVaR四种风险分配机制的算法,来仿真计算各银行的宏观审慎资本以及银行系统的倒闭情况,并展开对银行系统的宏观审慎监管分析。研究表明:1)除了2008年和2010年的Incremental VaR机制之外,2008年至2015年的四种风险分配机制下的宏观审慎资本都有效的降低了银行系统的平均倒闭概率,表明了对银行系统进行宏观审慎监管具有显著的效果。2)通过对各银行的资本变化及其倒闭情况的联合分析发现,在银行资本被重新分配的过程中,通常由大型银行,如:中国16家上市银行中的中国银行、交通银行、建设银行、工商银行及农业银行等,转移到小型银行,如:宁波银行、南京银行、平安银行及民生银行等。3)在四种风险分配机制中,ΔCoVaR机制的宏观审慎监管效果最为显著,每年都降低了银行系统的倒闭概率;相比之下,Incremental VaR机制下的宏观审慎监管效果则最差,该机制下对个别银行体现出明显的反向监管效果。4)Incremental VaR机制、Shapley value EL机制以及Component VaR机制下的宏观审慎资本与银行总资产呈现出一定的正相关,表明审慎资本主要受银行总资产的影响,因此这三种机制下审慎资本设定的比例可以让每个银行相同(该种设置方案与目前央行设定宏观审慎资本的政策一致);而ΔCoVaR机制下两者则呈不相关,但是其监管效果最为显著,因此该机制下各银行的审慎资本应该依据其对系统性风险的贡献来设定,可以设定各银行的宏观审慎资本的比例不同(目前央行可以借鉴该种方法进行监管)。以上的研究结论都对我国银行系统的监管具有一定的理论指导意义。此外,本文的研究目前是基于银行网络系统为全连接的情况,因此较少涉及到银行间的传染倒闭,未来的研究将考虑不同的网络结构对传染倒闭以及银行系统的宏观审慎监管的影响,进行深入探讨。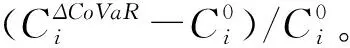
2 仿真计算
2.1 数据及仿真设置
2.2 仿真结果


3 宏观审慎监管分析
3.1 监管效果分析
3.2 宏观审慎资本与银行特性

4 结论
