基于情绪宣泄效用的邻避冲突演化博弈
2020-10-24俞武扬
俞武扬
(杭州电子科技大学 管理学院,浙江 杭州 310018)
0 引言
1977年,欧海尔(O’ Hare)[1]首次提出了“邻避”(Not In My Backyard,缩写为NIMBY)的概念,将邻避设施定义为一类具有负外部性的公共设施。最近十余年来我国民众抵制邻避设施的事件此起彼伏,学者们普遍认为我国已经进入了邻避时代。据统计2000年至2013年间,我国百人以上规模的群体事件中邻避冲突占比高达32%[2]。随着城市规模的不断扩大以及人们生活水平的逐步提高,现有的各种邻避设施(如垃圾焚烧厂、污水处理站)急需进一步规划建设,然而频繁发生的邻避冲突却又使得这些邻避设施的建设举步维艰,因此如何有效地化解邻避冲突已经成为了政府与学界的关注热点。
邻避冲突中政府行为对于民众的策略选择具有决定性的影响,以往学界的一个重要研究视角是分析政府行为对社区民众的风险感知以及风险积聚与扩散在邻避冲突中所起的作用。风险感知是人们对于客观风险的一种主观判断,个体的主观差异通常导致风险感知与客观风险之间存在较大的偏差[3]。学界认为引发邻避冲突的一个重要原因是由于不同群体对于邻避设施在风险感知上存在差异。如谭爽和胡象明[4]证实了对于核邻避设施,公众的邻避冲突行为与他们对于核设施的风险感知之间存在着强相关性;叶啸等[5]通过对多起邻避事件进行比较分析,指出政府公信力对于公众邻避设施的风险感知具有重要影响;陈云[6]认为不同群体关于邻避设施在风险感知度的多方面冲突是引发邻避冲突的重要原因。学者们也对邻避冲突中风险的积聚与扩散乃至群体性事件的演化过程进行了深入的研究。如毛庆铎和马奔[7]认为公众的有限理性、知识结构局限性、环境不确定性三者共同导致了客观风险的认知偏差;谭爽[8]认为公众焦虑心理在邻避风险从产生到转化为社会稳定风险的过程中起到了潜在的影响;侯光辉和王元地[9]提出了邻避风险链的概念,将邻避设施的客观风险、公众的感知风险、引发群体事件的社会风险这三者之间从概念、特征、决定因素和转化机制等方面进行了研究;黄杰[10]基于综合合风险治理框架研究了邻避冲突从感知到冲突之间的生成机理;陈玲和李利利[11]以北京某垃圾焚烧项目为例,研究了邻避风险转向社会稳定风险的触发机制。吕书鹏和王琼[12]从“风险-利益”感知差异的角度构建了地方政府与社区民众的决策框架并进行了多案例研究。从相关研究来看,学者们普遍认为政府行为对于民众的风险感知具有重要影响,这一影响贯穿于邻避事件发生的全过程,通过调节民众的内在心理机制改变危机走向(Hank et al.[13])。而从政府行为逻辑角度看,政府主要采纳业内专家意见进行封闭式决策,对邻避项目作出决定后进行宣布,当面临民众质疑之时则忙于为自己辩护,这套陈旧的政府管控模式已经无法适应当前的治理环境(王佃利等[14])。
综合上述文献分析可知,以往文献主要着眼于研究政府行为对社区民众在风险感知、聚集与扩散等方面的影响。何艳玲[15]通过分析一个典型的邻避冲突事件过程,指出“中国式”邻避冲突的演化具有螺旋式上升的态势。那么造成这种螺旋式上升态势的内在原因是什么?当前的研究视角只能解释邻避冲突的产生原因,而无法对邻避冲突演化的螺旋式上升态势提供有效的解释。本文尝试从情绪宣泄效用的视角研究邻避冲突演化的潜在原因,利用演化博弈论构建了基于情绪宣泄效用的邻避冲突演化博弈模型,分析地方政府与社区民众的演化均衡解,并进一步研究了纯策略演化均衡解的稳定性条件。利用数据计算对纯策略均衡解的演化稳定性结果进行了仿真。最后结合杭州中泰垃圾焚烧项目邻避冲突事件进行了案例研究,为邻避设施的规划建设给出了相应的结论和建议。
1 市政邻避设施规划风险沟通演化博弈模型
1.1 邻避冲突演化中的情绪宣泄效用分析
对邻避冲突进行理性分析首先需要厘清其中的利益相关者,这里“利益相关者”是指能够影响组织目标实现,或受组织实现其目标过程影响的所有个体与群体[16]。由于邻避设施本身是一种公共产品,因此邻避冲突的爆发涉及了诸多的利益相关者,如地方政府、社区民众、邻避设施开发商与运营单位、专家等[17],其中地方政府与受邻避设施影响的社区民众处于邻避冲突的核心位置,因此本文将地方政府与社区民众作为邻避冲突博弈演化的主体进行研究。
弗洛伊德认为人们会通过实施攻击行为释放自己的负面情绪,并从中得到快感[18]。情绪宣泄效用就是指当人们的负面情绪通过某种方式宣泄出来之后从心理上所获得的效用。一般而言,随着负面情绪程度的上升,采取更激烈的宣泄方式可以给带来更大的情绪宣泄效用。中国式的邻避冲突事件进程中,社区民众情绪宣泄效用的发展变化可以分为三个阶段:(1)温和宣泄阶段:在邻避设施规划公布的初期,由于社区民众对于邻避设施在风险感知上与地方政府存在偏差,因而对地方政府的邻避设施规划产生不满情绪,这一阶段社区民众的不满情绪处于稳定可控状态,因此民众通常会采取较为温和的行为宣泄自己的不满情绪,如向政府部门上访、请求行政审议、联名请愿等。(2)缓慢转变阶段:在社区民众向政府部门表达自身的意见与诉求之后,等待政府部门给出解决方案的过程中,社区民众的不满情绪呈现缓慢积累的状态,此时更为激烈的宣泄方式所能带来的情绪宣泄效用逐渐增加。(3)激烈宣泄阶段:当地方政府采取被动消极和封闭的策略(如敷衍民众、职能部门互相“踢皮球”、行政压制等)应对社区民众的温和抗议行为时,导致了社区民众的不满情绪突然高涨。这种高涨的不满情绪使得激烈的抗议手段(如破坏邻避设施建设、引发暴力冲突等)带来的情绪宣泄效用大幅增加。因此民众往往会倾向于选择这些激烈的抗议手段。这一阶段情绪宣泄效用的影响可能远远超过风险感知,尤其是在引发暴力冲突的场景中民众对于政府行为的强烈反抗情绪起了极其重要的催动作用(汪伟全[19])。
社区民众的情绪宣泄效用与他们的风险感知是有区别的,政府行为会对社区民众的风险感知产生影响,但这个风险感知值是相对稳定的,它不会随时间持续扩大或减小,而情绪宣泄效用则会随着不满情绪的不同持续地发生变化。因而社区民众情绪宣泄效用可以从内在动机上对于中国式邻避冲突表现出来的螺旋式演进态势提供较好的解释。
1.2 演化博弈模型假设
演化博弈论与经典博弈论最大的区别在于其放宽了对于博弈参与者完全理性的假设,通过借鉴社会生活中的学习模仿机制,演化博弈论假设参与博弈的主体通过学习他人策略,在不断调整自己策略的动态过程中达到博弈的均衡状态[20]。从博弈角度看,地方政府与社区民众并不是一开始就明确自己的最优策略,而是在学习与模仿他人经验的过程中不断调整策略,最终找到各自的最优策略从而实现博弈均衡。
假设1地方政府在邻避项目规划建设过程中针对社区民众有两种策略:协商沟通或封闭决策。协商沟通是指地方政府就邻避项目存在的风险、利益、补偿以及运营监管等问题与社区民众进行充分的协商与沟通,在争取社区民众理解与支持的前提下推进邻避项目。而封闭决策则指地方政府奉行邻避项目对于大众有利的原则,认为少数受影响的社区民众应该以大局为重,从而实行参考专家意见再由领导拍板决定的传统决策模式。设地方政府采取协商沟通策略的概率为p∈[0,1],采取封闭决策策略的概率为1-p。
假设2由于邻避设施的负外部性影响,社区民众在与政府博弈过程中可能引发的策略有三个:采纳接受、温和抗议以及暴力冲突。设社区民众群体中采纳接受的概率为q1,温和抗议的概率为q2,暴力冲突的概率q3,显然q1,q2,q3≥0,q1+q2+q3=1。面对政府的封闭决策模式时,除了所获得的客观收益之外,社区民众在采取温和抗议与暴力冲突这两种策略时存在不同的情绪宣泄效用。设温和抗议所能获得的情绪宣泄效用为A,而暴力冲突所能获得的情绪宣泄效用为B。这两个情绪宣泄效用值会随着社区民众不满情绪程度的上升而增加,且B的增加幅度大于A的增加幅度。
假设3考虑地方政府获得的收益是U,由于地方政府采取不同策略会影响社区民众对于邻避设施的正常价值感知,因此可设社区民众在政府协商沟通策略下获得的收益是V1,而在政府封闭决策下的收益为V2,V1>V2。地方政府采取协商沟通策略需要额外付出一定的成本C1,而社区民众选择温和抗议与暴力冲突的成本分别为C2,C3,可以假设暴力冲突所需成本大于温和抗议所需成本,即C3>C2。而当事态发展到民众用暴力冲突对抗地方政府的封闭决策之时,从维稳出发的最终结果都是邻避项目停止建设。基于结果与过程考核的角度,上级政府对于地方政府采取封闭决策的行为在事态轻微(社区民众采纳接受或温和抗议)时给予ω的惩罚值,而当事态严重(引发暴力冲突事件)时给予Ω的惩罚值,显然可设Ω>ω。
根据上述假设,可以构建地方政府与社区民众演化博弈的支付矩阵,如表1所示:

表1 地方政府与社区民众群体演化博弈的支付矩阵
1.3 演化博弈模型构建
G1=q1(U-C1)+q2(U-C1)+(1-q1-q2)(-C1)
(1)
G2=q1(U-ω)+q2(U-ω)+(1-q1-q2)(-Ω)
(2)
(3)
P1=pV1+(1-p)V2
(4)
P2=p(V1-C2)+(1-p)(A+V2-C2)
(5)
P3=p(-C3)+(1-p)(B-C3)
(6)
(7)
地方政府与社区民众在博弈的过程中知道不同策略所带来的收益,并且会随着对方策略的变化而调整自身策略,因此可以将政府与社区民众策略选择的概率p,q看作关于时间t变化的函数,从而得到双方的复制动态方程:
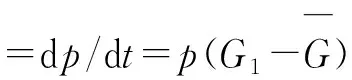
=p(1-p)[(Ω-C1)-(q1+q2)(Ω-ω)]
(8)
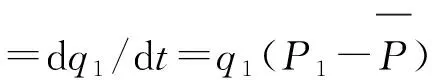
=q1[(1-q1)(P1-P3)-q2(P2-P3)]
(9)
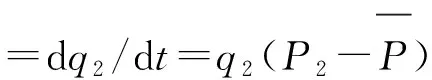
=q2[(1-q2)(P2-P3)-q1(P1-P3)]
(10)
其中:P1-P3=(C3+V2-B)+p(B+V1-V2)
(11)
P2-P3=(A-C2+C3+V2-B)+
p(B+V1-A-V2)
(12)
2 演化博弈均衡解及稳定性分析
地方政府与社区民众在策略对抗过程中不断获取相关信息,逐步调整各自策略,因此需要在双方策略相互影响的基础上分析其演化均衡解的情况及相关的稳定性。
在双方的复制动态方程中令f(p)=0,f(q1)=0,f(q2)=0可得到演化博弈的均衡解。当博弈双方都取纯策略时,该演化博弈所有的纯策略均衡解E(p,q1,q2)一共有六个,分别表示为:E1(1,0,0),E2(1,1,0),E3(1,0,1),E4(0,0,0),E5(0,1,0),E6(0,0,1)。而非纯策略均衡解是指博弈双方中至少有一方的策略不是纯策略时的博弈均衡解,下面先给出一个引理。
引理1当P1>P2>P3亦即P1-P3>P2-P3>0时,复制动态方程组{f(q1)=0,f(q2)=0}不存在非纯策略均衡解。
证明不妨设此时有P2-P3=G,P1-P3=G+δ,其中G,δ>0,此时复制动态方程组为:
f(q1)=q1[(1-q1)(G+δ)-q2G]=0
(13)
f(q2)=q2[(1-q2)G-q1(G+δ)]=0
(14)
分四种情况解上述方程组(13)、(14)可得:1)q1=0,q2=0;2)q1=0,[(1-q2)G-q1(G+δ)]=0易知该种情况解为q1=0,q2=1;3)q2=0,[(1-q1)(G+δ)-q2G]=0易知此时解为q1=1,q2=0;4)[(1-q1)(G+δ)-q2G]=0,[(1-q2)G-q1(G+δ)]=0且,将这两个方程等价变形为:q3(G+δ)+q2δ=0,q3(G+δ)+q2δ-δ=0,显然此时方程组无解。由上述四种情况可知方程组均不存在非纯策略均衡解,引理得证。
关于非纯策略均衡解,下面给出两个定理。
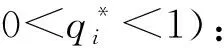
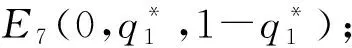
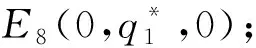
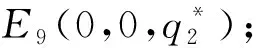
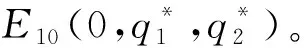
证明首先,当C1<ω时由于Ω-C1-(q1+q2)(Ω-ω)>q3(Ω-ω)≥0,以及当C1>Ω时有Ω-C1-(q1+q2)(Ω-ω)<-(q1+q2)(Ω-ω)≤0,可知f(p)=p(1-p)[(Ω-C1)-(q1+q2)(Ω-ω)]=0,必有p=0或p=1。
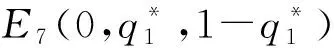
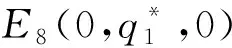
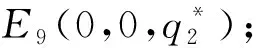
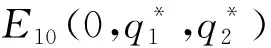
注:定理1给出了当p=0以及p=1时的非纯策略均衡解情况。
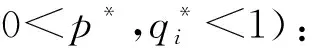
(1)当C1=Ω时,存在非纯策略均衡解为E11(p*,0,0);
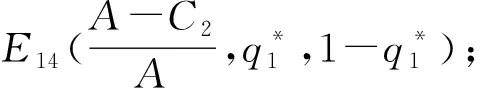
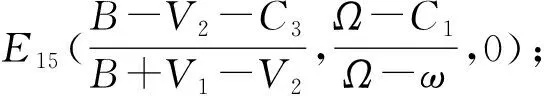
证明(1)当C1=Ω时,由f(p)=p(1-p)[-(q1+q2)(Ω-ω)]可知,当q1=q2=0时对所有的p*∈(0,1),E11(p*,0,0)为非纯策略均衡解;
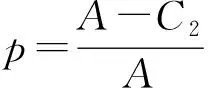
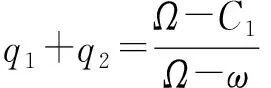
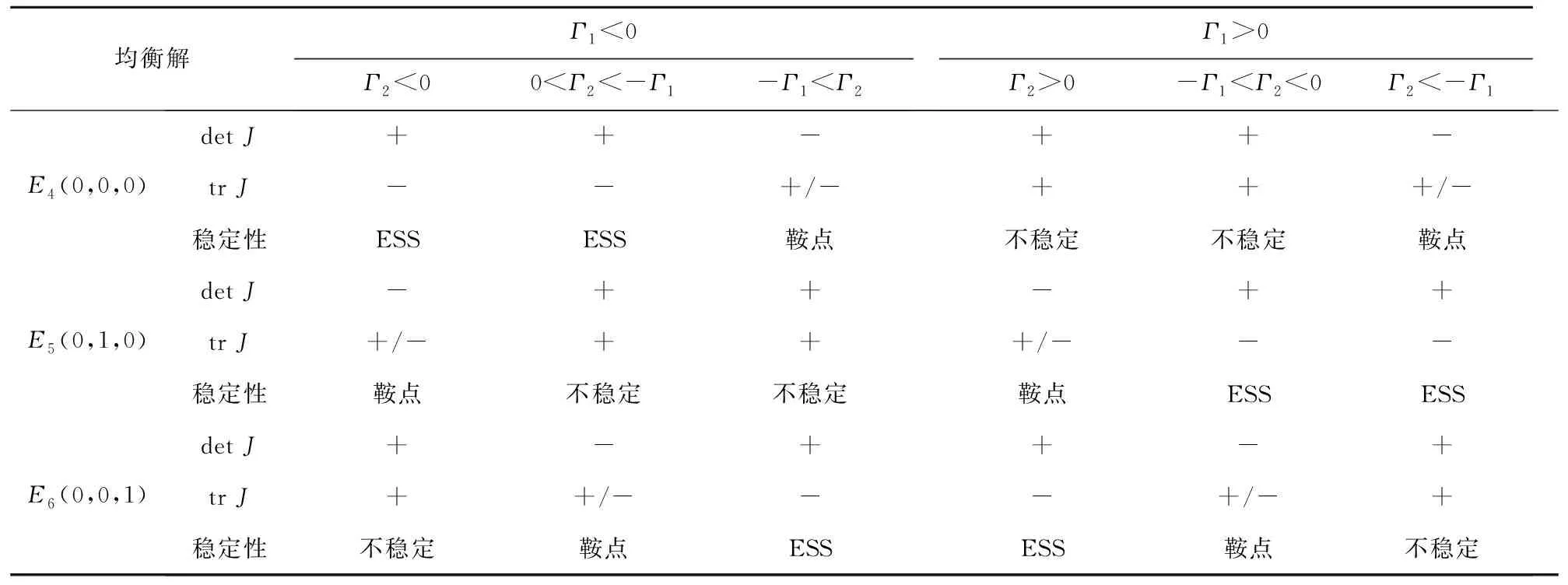
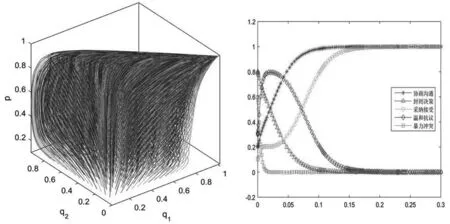
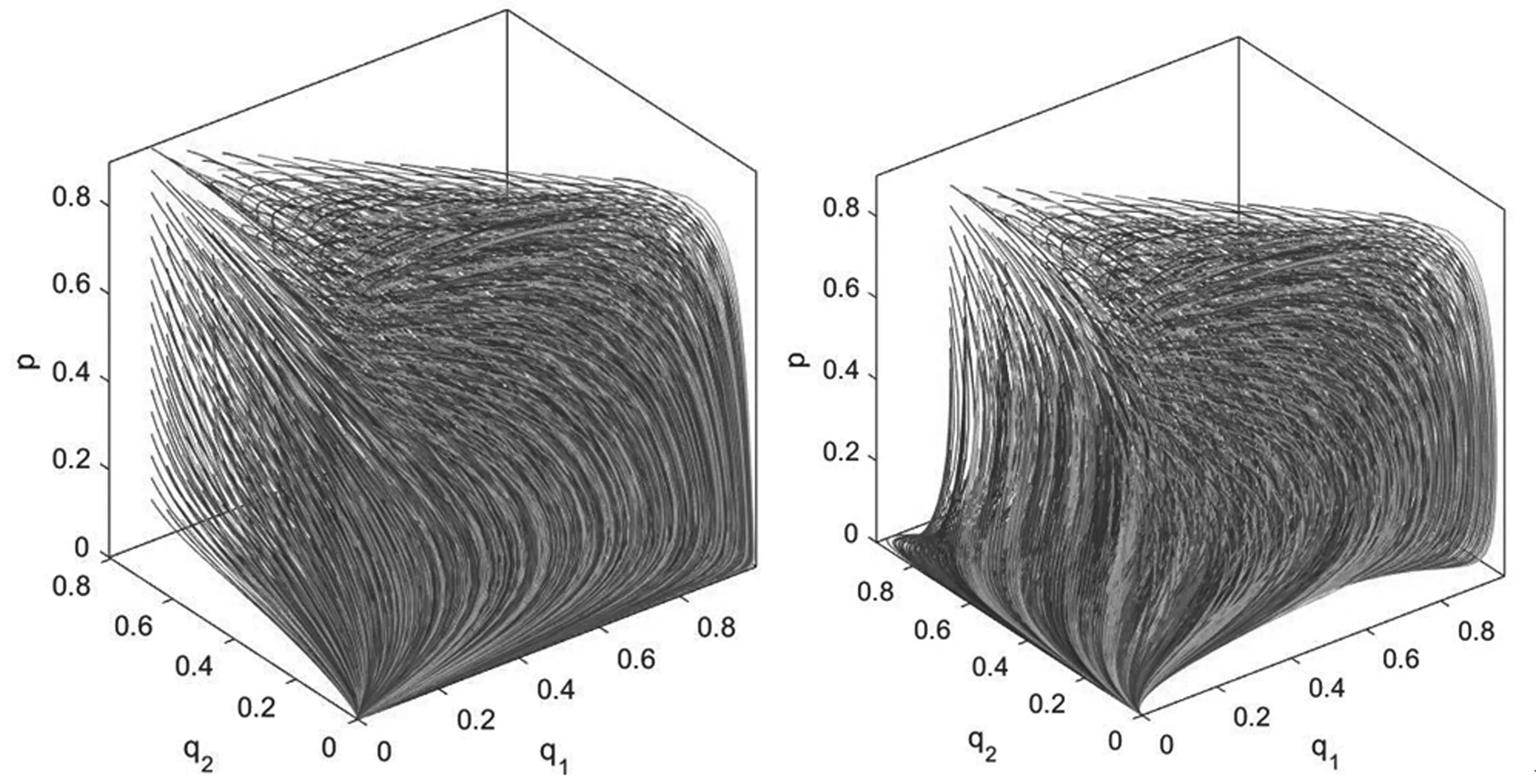
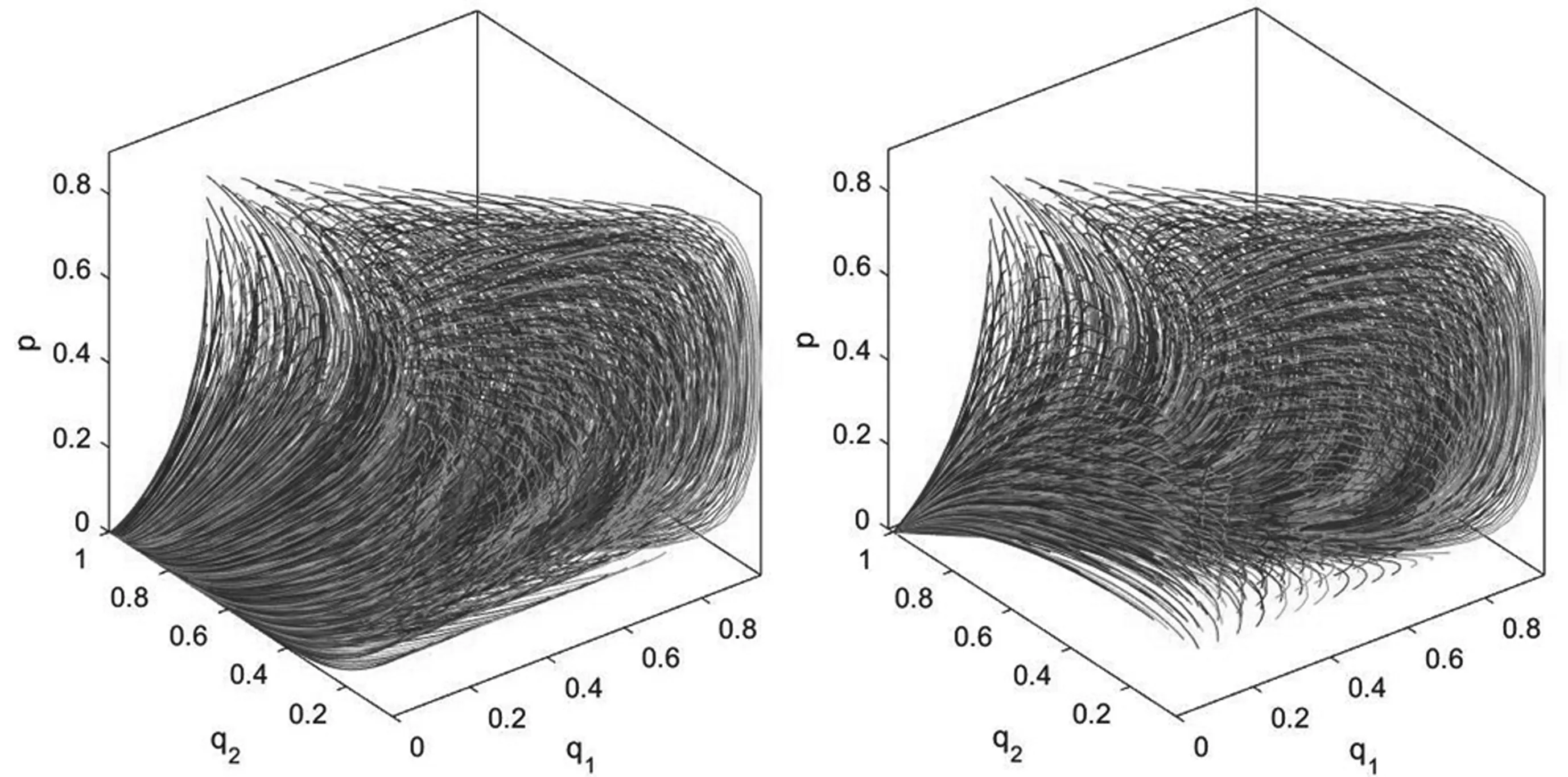
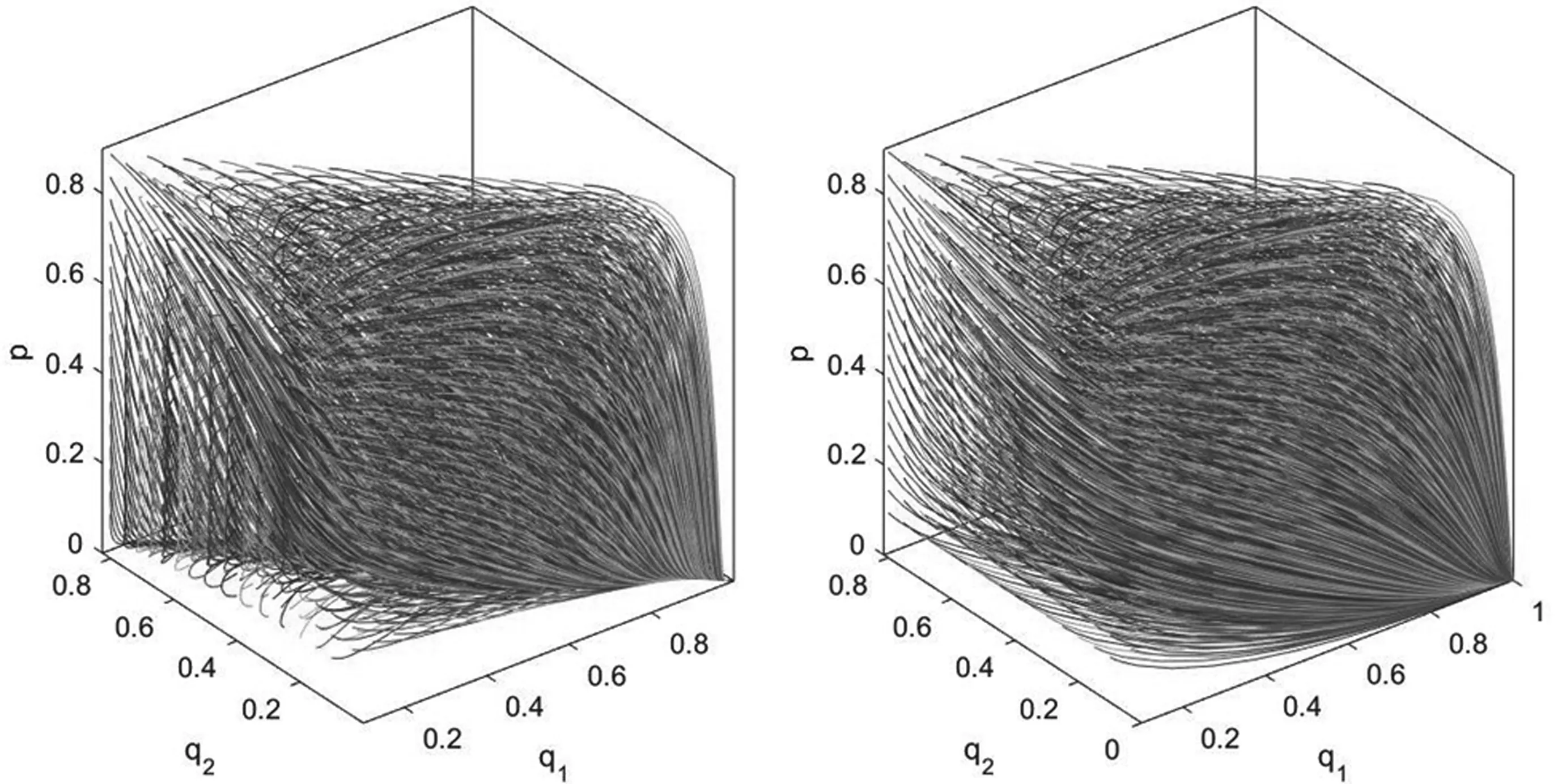
注:定理2给出了当0 由于博弈演化非纯策略均衡解情况众多,对于这些解的演化稳定性本文不去逐一分析。仅针对纯策略均衡解研究它们的演化稳定性。由于政府的纯策略为p=0或p=1,因此可以分两种情况分析。根据弗里德曼[22]提出的均衡点稳定性检验法,当雅可比矩阵J的行列式detJ和迹trJ同时满足detJ>0且trJ<0,说明该均衡点是演化稳定均衡策略解(ESS);如果行列式和迹同时满足detJ>0且trJ>0,表明对应的均衡点不稳定;如果矩阵行列式detJ<0,表明对应的均衡点为鞍点。由(9)、(10)两式得到雅可比矩阵J为: 首先,当C1<ω时,由Ω-C1-(q1+q2)(Ω-ω)>q3(Ω-ω)≥0可知dp/dt>0,所以此时必然有p*=1。而当p=1时,P1-P3=C3+V1,P2-P3=C3+V1-C2,代入上述雅可比矩阵J可得此时相应的纯策略均衡解的行列式与迹以及演化稳定性如表2所示: 表2 p=1时纯策略均衡解雅可比矩阵的行列式与迹及稳定性 其次,当C1>Ω时有Ω-C1-(q1+q2)(Ω-ω)<-(q1+q2)(Ω-ω)≤0,可知dp/dt<0,所以此时必然有p*=0。此时,P1-P3=C3+V2-B,P2-P3=A-C2+C3+V2-B;代入上述雅可比矩阵可得此时相应的纯策略均衡解的行列式与迹如表3所示: 表3 p=0时纯策略均衡解雅可比矩阵的行列式与迹 此时,行列式与迹的正负并不能够直接判断得到,因此需要分情况讨论如表4所示。为表示简洁起见,在表4中令Γ1=C3+V2-B,Γ2=A-C2。 表4 p=0时纯策略均衡解的稳定性 对于所构建模型的动态复制方程组(8)、(9)、(10),下面就纯策略演化均衡点是否都按前述稳定性分析所示渐进演化进行数值仿真。方程组所涉及参数按ESS点的不同分情况设定如下: (1)E2(1,1,0)为ESS点时:设其中的参数V1=400,V2=300,C1=100,C2=50,C3=150,A=100,B=100,Ω=300,ω=150。易知参数设置条件符合条件C1<ω,由表2可知此时E2(1,1,0)为ESS点,而E3(1,0,1)为鞍点。设(p,q1,q2)的初始值从0.1以步长0.05变化到0.9,且满足q1+q2≤1,利用Matlab R2015b对上述动态复制方程组进行求解,将解的演化进程绘制成图即为图1左图所示,无论初始概率如何,最终概率(p(t),q1(t),q2(t))都会稳定演化至E2(1,1,0),从图中还可以看到演化曲线在点E3(1,0,1)处呈现了鞍点效应。为对各项概率的变化情况有更清晰的认识,将(p,q1,q2)的初始值设为(0.2,0.1,0.3)后绘制各项概率随时间的演化过程如图1右图所示。民众采取温和抗议策略的概率先上升至0.8后再下降为0,表现出一种明显的鞍点效应。 图1 ESS为E2(1,1,0)时的仿真演化图 (2)E4(0,0,0)为ESS点:参数V1=400,V2=100,C1=400,C2=250,C3=350,A=200,B=650,Ω=300,ω=150,易知该组参数设置符合条件C1>Ω以及Γ1=C3+V2-B<0和Γ2=A-C2<0,因此由表3可知此时E4(0,0,0)为ESS点而E5(0,1,0)为鞍点。与(1)中同样方法设置(p,q1,q2)的初始值绘制演化曲线如图2左图所示。保持上述参数设置不变,仅重新设置A=350,可知此时0<Γ2=A-C2<-Γ1,此时E4(0,0,0)为ESS点而E6(0,0,1)为鞍点,同样绘制曲线图如图2右图所示。从图2中可以看出,无论初始概率如何,最终概率(p(t),q1(t),q2(t))都会稳定演化至(0,0,0)。 图2 ESS为E4(0,0,0)时的仿真演化图 (3)E6(0,0,1)为ESS点:设参数为V1=400,V2=100,C1=400,C2=250,C3=350,A=500,B=650,Ω=300,ω=150,易知该组参数设置符合条件C1>Ω以及Γ1=C3+V2-B<0,-Γ1<Γ2=A-C2,因此由表3可知此时E6(0,0,1)为ESS点而E4(0,0,0)为鞍点,其概率解的演化进程如图3左图所示。同样保持参数设置不变,仅重新设置B=100,可知此时符合条件Γ1>0,Γ2>0,由表3可知此时E6(0,0,1)为ESS点而E5(0,1,0)为鞍点,绘制演化图如图3右图所示。从图3中可以看出,无论初始概率如何,最终概率都会稳定演化至(0,0,1)。 图3 ESS为E6(0,0,1)时的仿真演化图 (4)E5(0,1,0)为ESS点:设参数为V1=400,V2=300,C1=400,C2=200,C3=350,A=180,B=550,Ω=300,ω=150,易知该组参数设置符合条件C1>Ω以及Γ1=C3+V2-B>0,-Γ1<Γ2=A-C2<0,因此由表3可知此时E5(0,1,0)为ESS点且E6(0,0,1)为鞍点,其概率解的演化进程如图4左图所示;同样保持参数设置不变,仅重新设置A=30可知此时Γ2=A-C2<-Γ1, 因而此时E5(0,1,0)为ESS点且E4(0,0,0)为鞍点,其概率解的演化进程如图4右图所示。 图4 ESS为E5(0,1,0)时的仿真演化图 杭州市中泰垃圾焚烧发电项目从2014年的邻避冲突事件到2017年的建成运营,同一项目在不同阶段呈现了不同的结果,为本文的博弈模型提供了一个极佳的案例。该项目发展过程实际上可按杭州市政府所采取的不同策略分别进行分析如下: (1)政府采取封闭决策策略 2012年8月,杭州市政府启动了中泰垃圾焚烧发电项目并于2013年10月论证了建设地点。2014年3月29日,中泰垃圾发电项目在杭州市政府官方网站进行了公示。2014年4月23日,媒体报道后引起了附近居民对于该项目污染情况的担忧,居民通过论坛、微博等网络平台表达不满情绪,并于4月24日向杭州市规划局递交了请愿书,但是并未获得官方回应。5月7日,垃圾焚烧厂单方面动工建设引发了当地居民的强烈抵抗。5月9日至10日当地民众采取高速堵路的激烈对抗方式并与特警发生冲突事件,随后杭州市政府官方承诺“在没有履行完法定程序和征得大家理解支持的情况下一定不开工”。 这一阶段,政府采取的策略是封闭决策,由于与社区民众的协商与沟通措施明显不足,导致附近居民直至媒体报道后才了解该项目的存在,从而滋生了对政府决策过程的不满情绪。从4月23日至5月6日,此时民众的不满情绪相对较低,可以视为民众的情绪宣泄效用处于温和宣泄阶段。在该阶段的参数具有Γ1>0,Γ2>0或是Γ1<0,Γ1+Γ2>0的特征,也即有C3+V2-B>0,A-C2>0或是C3+V2-B<0,A-C2+C3+V2-B>0这两个条件都意味对于社区民众而言,采取“温和抗议”的策略所获得的收益大于“采纳接受”与“暴力冲突”这两种策略相应的收益,因此社区民众所采取的策略是通过网络平台发声以及递交请愿书等相对平和的方式与政府进行博弈,此时演化结果如图3所示。自4月25日至5月6日,民众的情绪宣泄效用处于缓慢转变阶段,此时民众对于政府的不满情绪逐渐积累,更为激烈的抗议方式所带来的情绪宣泄效用逐渐增加。而从5月7日到5月10日,由于前阶段民众不满情绪的不断积累,同时政府单方面动工建设的行为使得民众的不满情绪达到高潮,因而民众的情绪宣泄效用进入激烈宣泄阶段。采取“暴力冲突”这一策略对于民众而言具有极大的情绪宣泄效用,亦即此时参数B的值大幅增加,这就导致A-C2+C3+V2-B<0,此时博弈条件变化为Γ1<0,0<Γ2<-Γ1,从而使得博弈演化至如图2右图所示,事件最终以邻避项目停建告一段落。 此次过程中民众从温和抗议发展到暴力冲突,在形式上表现出“中国式”邻避冲突演化过程中典型的螺旋式上升态势。而从博弈分析的观点来看,情绪宣泄效用起到了推动博弈均衡解从(封闭决策,温和抗议)向(封闭决策,暴力冲突)演化的作用,说明基于情绪宣泄效用的演化博弈模型可以有效地解释“中国式”邻避冲突螺旋式演进的内在原因。 (2)政府采取协商沟通策略 2014年7~9月,垃圾焚烧项目所属中泰街道在社区民众中组织了82批4000多人次赴外地考察先进垃圾焚烧厂;通过召开中泰垃圾焚烧项目答辩会,与社区民众进行充分的双向交流与沟通,以降低社区民众对于垃圾焚烧项目的风险感知;余杭区选调1000多名曾熟悉当地情况的机关干部,走访社区民众2.5万人次,搜集关于垃圾焚烧项目的意见建议500多条。杭州市拨给中泰街道1000亩土地指标,用于保障当地产业发展以弥补民众的利益损失;余杭区投资20.8亿元从环境补偿角度打造城郊休闲“慢村”,并投入1.4亿元实施117项改善环境的实事工程,对承担垃圾处理的区域设立环境改善专项资金进行补偿;成立群众监督小组赋与现场监督权,实时公布焚烧厂每天的排放指标,使项目真正公开透明。 这一阶段,政府与社区民众进行了多方面的协商沟通。一方面使社区民众对垃圾焚烧项目的认知更加科学,从降低了对该垃圾焚烧项目的风险感知偏差;另一方面通过诚恳的沟通协商过程,充分表达出地方政府倾听社区民众呼声、切实把人民利益放在心中的态度,从而有效地降低了社区民众对于政府行为的不满情绪。再通过切实可行的全方位补偿方案,使得社区民众进一步提升了接纳项目的主观意愿。这一系列的协商沟通措施,体现至本文模型中可以解释为使民众采用温和抗议及暴力冲突这两种策略在情绪上的宣泄效用A,B得以下降,同时使得原先民众感知的垃圾焚烧项目的价值V2转变为更大的V1,因而双方的均衡解演化至(协商沟通,采纳接受)。最终中泰垃圾焚烧项目于2015年4月在原址顺利开工建设,并于2017年9月投入试运营,使得中泰垃圾焚烧项目成功破解邻避困境,成为了一个双方共赢的惠民工程。 根据以上演化博弈以及案例研究结果,可得如下结论:(1)地方政府采取何种策略取决于各种策略所需成本以及与上级政府考核要求之间的权衡;(2)政府采取封闭决策的措施,虽然可以在前期提高邻避项目进展的速度,但是这种策略不但影响社区民众对于邻避项目风险的客观认知,而且还会使民众对于政府的决策态度滋生不满情绪,进而导致后续事态恶化,反过来又会影响整个项目的进程;(3)邻避冲突过程中,民众对于邻避项目的风险感知、不同抗议方式的成本等因素一般不会发生太大的变化,然而不同抗议方式的情绪宣泄效用却随着民众不满情绪的变化存在着很大的不同,为邻避冲突事件的螺旋式演化态势提供了一种合理的解释。 根据本文的演化博弈模型分析结论,目前我国污染类邻避事件的治理重点应该关注如下几方面:(1)首先,上级政府对于地方政府的考核机制不仅要从绩效指标着手,还应该考虑过程指标,明确在邻避事件过程中地方政府的策略选择必须要以服务人民为宗旨,以群众的满意度为目标。(2)政府采用协商沟通策略存在两方面作用,一是提高民众对于邻避项目的价值感知(降低风险感知偏差),二是提高民众对于采纳接受策略的情绪正向效用(对政府行为在情感上的认同感);因此邻避项目建设需要加强相应的协商沟通机制建设,降低民众对于邻避设施负外部性的过高认知,这一过程需要用多种方式(如利用书籍、宣传册、标语等传统方式以及利用实地考察等方式)对于邻避项目进行科学宣传,加强民众的主观感受与科学认知。在建设与运营过程中赋与群众充分的监督权,从而降低民众对项目建设与运营过程的忧虑情绪。(3)政府采取封闭决策同样存在着两方面影响,一是降低了民众对于邻避项目的价值感知(风险感知偏差增大),二是导致民众对政府决策行为的方式滋生不满,从而使得民众采取反对抗议策略(温和抗议与暴力冲突)带来的情绪宣泄效用增强。(4)为了促进邻避项目的顺利进行,对受影响的民众进行补偿在一定程度上可以降低民众的不满情绪。考虑到邻避项目对于社区民众存在多方面影响,政府应该采用多元的补偿形式(如经济补偿、环境补偿、生态补偿等)对民众从物质与精神等各方面提供必要的协助与补偿。 致谢:作者对匿名审稿专家所提的建设性意见表示衷心感谢!

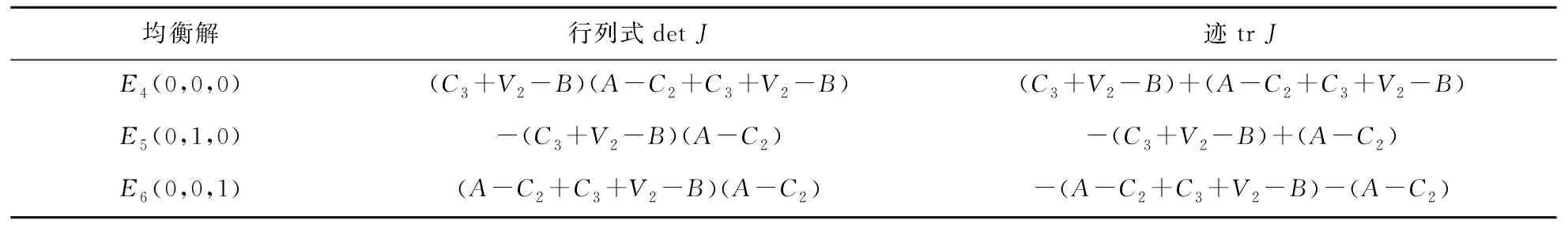
3 数值仿真分析
4 案例研究
5 总结
