基于直觉模糊化的广义模糊时间序列预测模型
2020-10-24田宗浩
王 鹏,田宗浩
(陆军炮兵防空兵学院 基础部,安徽 合肥 230031)
0 引言
模糊时间序列[1~5](Fuzzy Time Series, FTS)在含糊、不确定信息处理中广泛应用,并且具有良好的鲁棒性和泛化性。近年来,广义模糊时间序列预测模型被提出[6~9],其充分考虑样本数据对模糊集的隶属情况,把要考虑的隶属度值作为预测模型的权重,建立不同层次的模糊逻辑关系,提高了模型的可解释性和预测精度。但是,通过对广义模型的深入研究发现,只利用隶属度函数描述样本数据对模糊集的隶属情况,在数据模糊化过程中不能形象地反应信息的含糊、不确定性。随着人们对问题认识的不断深入,样本数据对模糊集的隶属情况会表现出一定的犹豫程度,如何更好的表达样本数据对模糊集的隶属状态成为一个研究的热点问题。
Zadeh教授提出的直觉模糊集[10](Intuitionistic Fuzzy Set, IFS)是模糊集理论的扩展和补充,通过增加一个非隶属度参数来描述事物“非此非彼”的模糊特性。直觉模糊集的数学描述更加符合事物的模糊本质,为处理不确定信息提供了新的研究思路。但是,如何确定IFS的隶属度和非隶属度函数呈现很大的复杂性,如何将样本数据直觉模糊化和描述样本数据对模糊集的隶属情况成为模型改进的一个瓶颈问题。为此,本文结合文献直觉模糊化的方法以及采用记分函数来描述样本数据对模糊集的隶属情况的思想,建立基于直觉模糊化的广义模糊时间序列模型,并通过仿真实验对模型的有效性和可行性进行验证。
1 基础理论
为建立模型需要,本节给出了IFS和FTS的相关定义:
定义1[10]Atanassov对直觉模糊集进行如下定义:A={
A为有限论域X上的直觉模糊集,如果A为正规直觉模糊集, 其满足下面三条性质:
(1)0≤μA(x)≤1,0≤γA(x)≤1;
(2)0≤μA(x)+γA(x)≤1,0≤πA(x)≤1;
(3)μA(x)+γA(x)+πA(x)=1。
定义2实数集R的一个子集Y(t),(t=1,2,…)表示论域,在论域Y(t)上定义n个模糊集Ai(i=1,2,…,n),其隶属函数为fAi(t),F(t)是fAi(t)的集合,则F(t)就定义为论域Y(t)上的一个模糊时间序列。
定义3假设状态F(t+1)由F(t)转移得到,则F(t+1)的一阶模型可以表示为F(t+1)=F(t)R(t,t+1),则称R(t,t+1)为F(t+1)和F(t)之间的模糊逻辑关系[13,14]。
根据上述FTS以及模糊逻辑关系的定义,广义模型中两个观测值之间的模糊逻辑关系可以描述为:
设论域U被划分为k个模糊子区间U={u1,u2,…,uk},相应的模糊集可以表示为A1,A2,…,Ak。则时刻观测样本数据xt对每个模糊集的隶属度可以表示为:
同理,t+1时刻观测样本数据xt+1的模糊状态表示为:


通过分析建立的k2个模糊逻辑关系,有些对模型的预测结果影响微乎其微,过多的考虑反而会引入一些冗余信息、增加模型的计算复杂度。为此,结合唯物辩证法中“突出主要矛盾”的思想给出定义4的特殊形式。

2 基于直觉模糊化的广义模糊时间序列预测模型
FTS的关键是挖掘历史数据内部的模糊变化和不确定特性,掌握序列数据随时间的变化规律,提高预测精度.IFS的“非此非彼”性,以及实际状态变换的不确定性。因此,本文从数据直觉模糊化以及记分函数的选取入手,以文献[6~8]建立的广义模糊时间序列模型为基础,构建基于直觉模糊化的模糊时间序列预测模型。
2.1 论域划分及序列数据直觉模糊化处理
笔者为简化建立模型的计算复杂度,采用等分论域划分方法对数据进行处理。假设U为论域,xmax和xmin分别为观测样本的最大值和最小值,则
U=[xmax-σ1,xmax+σ2]
(1)
其中,σ1和σ2为合适的正整数。
结合数据的实际含义,用自然语言能够表述的方法对论域U进行模糊划分,其相应的模糊概念为Ai。由于人认知的模糊性,对论域的划分不能够太细,因此设定划分的子区间个数为k,则子区间长度l为:
(2)
其中:D为论域范围。
由此得论域划分的结果为:
(3)
其中:u1=u2=…=uk=l,d1=xmin-σ1,dk+1=xmax+σ2,mi为第i个模糊子区间的中间值。
现实中给出的样本数据大多为实数集,为此需要对样本数据进行直觉模糊化处理以满足建模的需要,本文通过在隶属度和非隶属度函数中增加犹豫度因子δ来描述样本数据对模糊集的不确定性,如式(4)所示:
(4)
其中,xt为样本数据;l为等分论域区间间隔;mi为对应子区间的中间值;δ为犹豫度因子,表示数据隶属集合的不确定程度。结合定义2,可以证明式(4)为正规直觉模糊集。当δ=0时,πi=0,直觉模糊化就退化为普通模糊化。
在传统的数据模糊化过程中利用最大隶属度原则来确定样本数据所对应的模糊集,而在直觉模糊化过程中引入了非隶属度函数,并用直觉指数来描述数据的中立状态,极大地扩展了模糊集的表达能力,但是也就如何根据直觉模糊化的结果确定样本数据所对应的模糊集增加了难度。在一般的直觉模糊变换中采用最多的为“ ∨(取大)-∧(取小)”运算,其特点是突出主要因素,忽略一些次要信息,也正是其丢失了一些信息,从而影响了模型的预测精度,使问题偏离实际。为此,本文在如何评判数据的隶属问题时引入记分函数的概念,综合考虑直觉模糊集中支持、反对以及中立三者之间的关系,使评判结果更加合理。
文献[15~17]给出了大量有关记分函数的研究成果,其中李凡在文献[17]中给出了记分函数的一般形式,其它记分函数均为式(3)的特例。
L(Ai)=θ1μAi+θ2γAi+θ3πAi
(5)
理论上讲,式(5)充分考虑了直觉模糊集中支持、反对以及中立三个方面的信息,是很好的结果,但θ1,θ2,θ3三个系数的确定是一个难点,也制约了记分函数一般形式的推广应用。为了解决记分函数参数难以确定的问题,文献[15]给出了记分函数的特殊形式,并得到大量专家学者的认同。为此本文也拟采用式(6)为记分函数。
(6)
其中,式(6)的含义为:在直觉指数描述的中立状态中,支持和反对的程度处于均衡状态,该方法简单方便,易于处理,为问题的解决提供了新的思路。当πAi=0时,记分函数就退化隶属度函数。
2.2 确定记分函数值向量中要考虑的个数,并做归一化处理
利用公式4将数据直觉模糊化,结合公式6得到观测样本数据对每个模糊子集的记分函数值向量(LA1(t),LA2(t),…,LAk(t)),以此描述对各个模糊集的隶属程度。将观测样本对每个模糊集的记分函数值按照从大到小的顺序的排序。设定要考虑的最高记分函数值个数为p,Lp(t)为记分函数值向量中的第p高的记分函数值,引入式(7)对记分函数值向量标准化:
(7)
标准化后的记分函数值向量不仅包括最高记分函数值所对应的位置信息,还包括其它要考虑记分函数值的位置信息,这样对观测样本的初始信息的利用率较高。
根据标准化的记分函数值向量,利用公式(8)对记分函数值向量进行归一化,为预测确定权重。
(8)
其中,k为划分模糊概念个数,α为模糊参数,α∈(0,+∞)。
2.3 依据训练数据的先后建立模糊逻辑关系及关系矩阵
2.4 预测及去模糊化
根据要考虑的最高记分函数值的个数以及第p个最高记分函数值对应的模糊概念Ai,利用3.3节建立的关系矩阵R(p),分别得到第p个最高记分函数值对应的预测值Fvalp(t+1)
(9)
其中,R(p)为第p大隶属度对应的模糊逻辑关系矩阵。
利用得到P个预测值,结合式(8)归一化后的记分函数值向量作为第P个最高记分函数值Fvalp(t+1)对应的预测值的权重值,为此可以得到最终的预测值为:
(10)
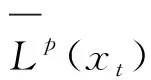
为了说明模型的有效性,利用均方误差RMSE和平均百分比相对误差MAPE来衡量模型的预测精度:
(11)
(12)
其中,xt为样本数据,Fval(t)为其对应的预测值。
3 算例分析
为验证本文建立模型的有效性和科学性,遵照上文建立模型的过程,利用典型的Alabama大学22年的入学人数为实验数据,分别以Chen和Lee模型模糊逻辑关系矩阵建立的方法,与普通模糊化的广义模型进行对比分析。
依据3.1节均等论域划分方法,将样本数据划分为7个模糊子区间,以1000为区间长度,则每个子区间为:u1=[13000,14000],…,u7=[19000,20000]。
由于Alabama大学22年的入学人数为实数集,而模型要求样本集为直觉模糊集,应用式(4)对样本数据直觉模糊化,当δ=0.2时,直觉模糊化结果如下所示:
通过喷嘴性能曲线(图2)和实际喷嘴雾化实验效果(图3)可以确定新喷嘴在雾化性能方面、喷射扇形角度和喷嘴流量线性比旧喷嘴优异。

依据样本数据的直觉模糊化结果,结合式(6)记分函数得到样本数据对各个模糊集的记分函数值,结果详见表1。
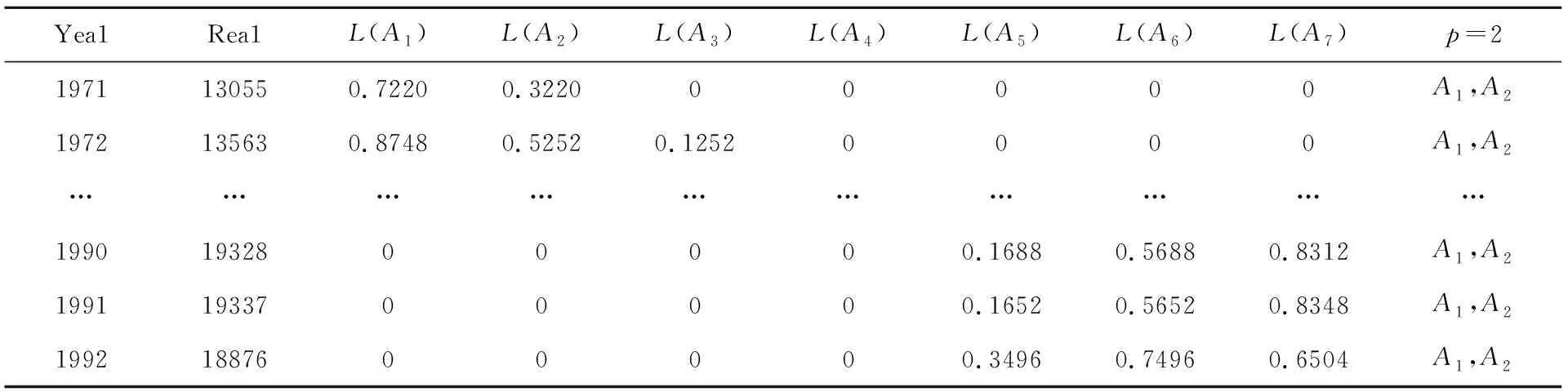
表1 样本数据的记分函数值
为与普通模糊化广义模糊时间序列模型对比分析的需要,假设p=2,α=1,依据表1中样本数据对各个模糊集的记分函数值,可以得到两个广义模糊逻辑关系组FLR(1,1)和FLR(2,1):
(1)FLR(1,1)
A1→A1,A1→A1,A1→A2,A2→A3,A3→A3,A3→A3,A3→A3,A3→A4,A4→A4,A4→A4,A4→A3
A3→A3,A3→A3,A3→A3,A3→A3,A3→A4,A4→A6,A6→A6,A6→A7,A7→A7,A7→A6
(2)FLR(2,1)
A2→A3,A2→A3,,A2→A3,A2→A3,A4→A4,A5→A6,A5→A6,A7→A7,A6→A7,A6→A6
依据上述最高记分函数值以及次高记分函数值对应的模糊逻辑关系集合FLR(1,1)和FLR(2,1),分别应用Chen和Lee三种模糊逻辑关系矩阵的确定方法,得到相应的模糊关系矩阵为:
3.1 Chen模糊关系矩阵
3.2 Lee模糊关系矩阵
结合样本数据隶属于各个模糊子集的记分函数值(表1)以及设置的需要考虑的记分函数值个数p,分别利用式(7)和(8)对记分函数值进行标准化和归一化,并将归一化后样本数据的记分函数值向量作为预测值的权重。参照Chen和Lee提出的预测规则,利用式(9)分别求出第p大记分函数值对应模糊子集对下一时刻的预测值Fvalp(t+1),然后采用式(10)求解出模型的最终预测结果。下面以Chen模型为例求解预测值,例如:1971年的样本数据对各个模糊集的记分函数值向量为(0.7220,0.3220,0,0,0,0,0),观测值对应的模糊集为A1和A2,归一化后的记分函数值向量为(0.6916,0.3084,0,0,0,0,0),最高记分函数值对应的模糊子集为A1,其预测主要用到的模糊关系对应于RC(1)的第一行,此时的预测值Fval1(1972)为14000;次高记分函数值对应的模糊子集为A2,用到的主要模糊关系为RC(2)的第二行,此时的预测值Fval2(1972)为14500,则1972年的最终预测值为0.6916×14000+0.3084×14500=14500=14154。类似的可以得到其它各年以及Lee模型的预测结果,表2为普通模糊化广义模型在p=2,α=1时预测结果和本文直觉模糊化广义模型分别在Chen和Lee模型上应用的预测结果,最后两行分别为对应模型的均方误差和平均百分比误差。

表2 p=2,α=1广义模型预测结果对比
其中,Model1为p=2,α=1时普通模糊化的广义Chen模型;Model2为p=2,α=1时普通模糊化的广义Lee模型;Model3为p=2,α=1时直觉模糊化的广义Chen模型;Model4为p=2,α=1时直觉模糊化的广义Lee模型。
糊集的隶属情况,其对应预测结果的精度得到提升。另外,图1中模型3和4的预测结果曲线更贴近真实值,尤其是1987年到1989年的预测精度更有了显著提升,进一步验证了本文建立的直觉模糊化的广义模型的有效性和可行性。
为研究犹豫度因子对样本数据直觉模糊化的影响,表3和表4给出了不同犹豫度的情况下Chen和Lee模型的预测精度变化情况。
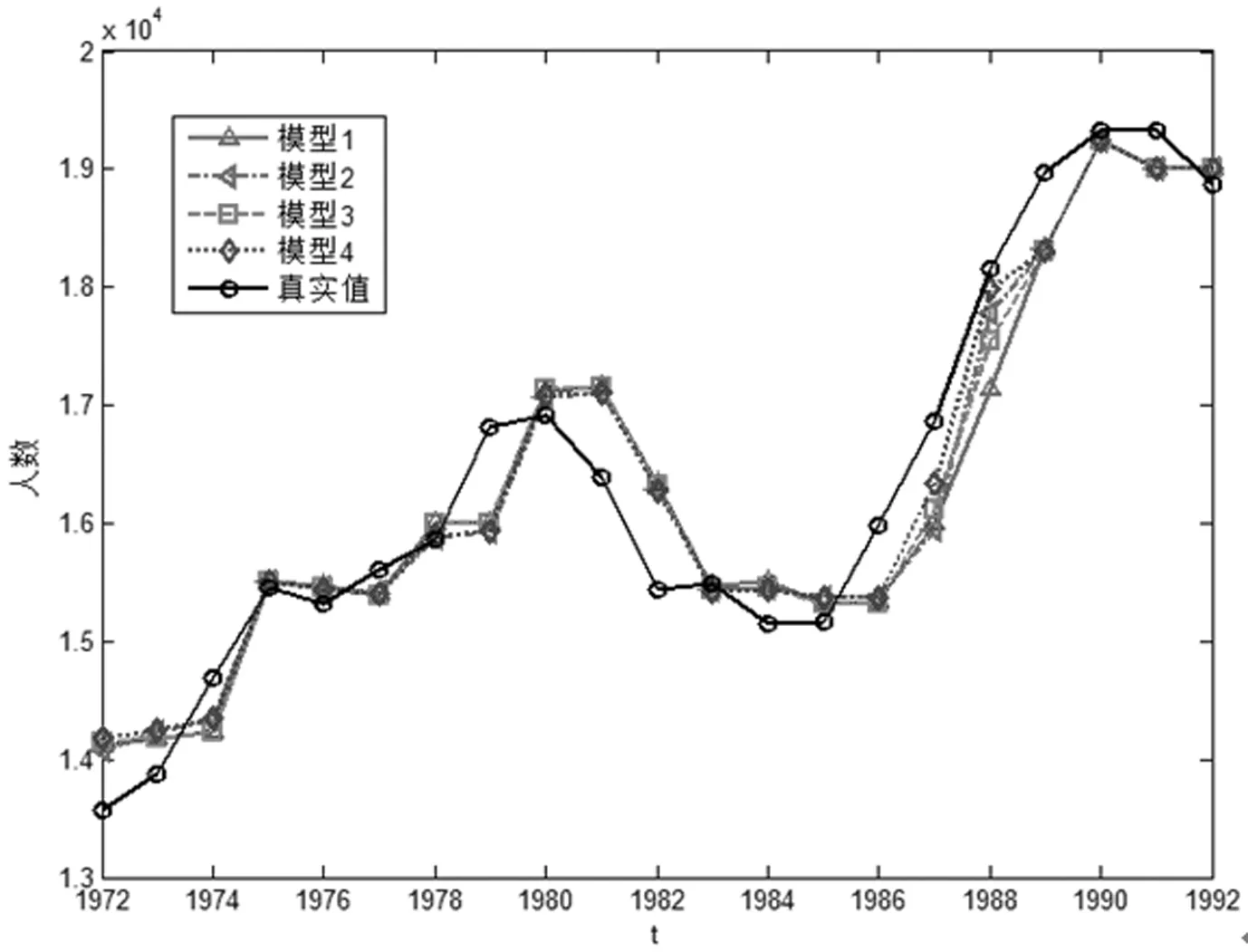
图1 p=2,α=1时四种广义模型预测结果对比

表3 不同犹豫度情况下Chen广义模型预测精度表

表4 不同犹豫度情况下Lee广义模型预测精度表

图2 不同犹豫度情况下模型预测精度变化曲线
对表3和4分析可知,犹豫度因子的选取影响着模型的预测精度,当δ=0.2时,本文模型取得最好的预测结果, 直觉模糊化的广义模型的可行性和有效性得到验证。
但是通过图1分析发现,每年的预测结果精度提高并不是很明显,这是由于式(6)记分函数在犹豫度所表达的中立状态中,支持和反对的程度均衡引起的。显然,当样本数据越接近中间值时,样本数据对相应模糊集的隶属情况越明确,支持程度越高;相反,反对的程度越高。为此,合理的确定样本数据对各个状态的记分函数影响着模型的预测精度,能够更加客观地描述样本数据“非此非彼”的模糊状态。
4 结论
文章分析了传统FTS的局限性,引入直觉模糊集对FTS进行扩展。通过样本数据直觉模糊化,加深了对数据模糊性的认识,较好的反映了数据“非此非彼”的不确定性本质;更加细腻的描述了模糊现象的本质。最后通过实例验证和对比分析,验证了本文所建立的模型有较好的预测性能。但是,文中也分析了本文建立模型存在的不足,指出犹豫度因子的选取影响着模型的预测精度。另外,本文用记分函数来描述样本数据对模糊集的隶属情况,如何合理的确定记分函数也是影响模型预测结果重要因素,这也将是今后研究的重点。
