考虑更新延长两阶段保修的二手产品维修策略优化
2020-10-23罗运鹏
董 克, 罗运鹏
(安徽广播电视大学 经济与管理学院,安徽 合肥 230022)
0 引言
近年来,随着人们环保意识的增强和节约成本的考虑,二手产品(如汽车、笔记本等)越来越受到人们的青睐。对于顾客而言,二手产品的价格固然低廉,但他们同样也关注于产品的性能。如何保证自己所购买的产品能在使用期限内完成所期望的任务,是他们最关心的问题。因此,二手产品维修问题已逐渐成为当前学者研究的热点。
针对产品保修和维修问题,一些学者进行了系统的研究,这方面的文章有[1~4]。通常地,为保证产品的正常运行,顾客在购买产品的同时,将选择经销商提供的某种保修策略。目前,基本的保修策略主要有两种:更新保修策略和非更新保修策略。所谓更新保修,是指当产品发生故障时,对产品进行更换,更换成本有两种分摊形式:一种是全部由经销商承担;另一种是由经销商和顾客依据设备已运行的年龄按比例分摊。在更换的同时,保修期限也进行更新。所谓非更新保修,是指制造商仅负责基本保修期内的产品维修服务,当产品发生故障时,保修期限不更新,一旦保修期满,保修终止。除上述两种保修策略之外,学者们还提出了其它保修策略模型[5~7],此外,还有一些将上述保修策略结合在一起进行研究的文章[8~11]。上述研究中,尽管经销商提供了多样的保修策略,但主要集中在基本保修方面,远远不能满足顾客的需求。因此,经销商又提供了各种延长保修策略供顾客选择。Lam等[12]提出了一个在免费保修策略下的延长保修策略模型;Wu等[13]从顾客的角度出发,研究了带有基本保修和延长保修策略的产品的生命周期成本优化问题;Bouguerra等[14]研究了在延长保修期间,对发生故障的产品进行免费小修的策略问题。但是,均没有考虑到当延长保修期满之后的产品维修问题;Jung等[15]以顾客维修总费用率最小为目标,研究了新产品的最优维修期问题;Park等[16]提出了带有维修时间限制的更新延长保修策略;文献[17]从顾客的角度出发,研究了当保修期满后对产品进行不完美维护,并且在产品的年龄达到某个值时进行更换的优化策略;Park等[18]还提出了基于二维保修期满的周期预防维护策略。文献[19]从制造商的角度出发,研究了带二维延长保修产品的两阶段维护优化问题;Yang等[20]研究了在二维保修策略下,通过考虑产品的使用率来预测其故障数的问题;文献[21]分别从顾客和制造商的角度,研究了带二维保修产品的周期预防维护优化问题;Wang等[22]研究了带维修时间限制的二维修保修期满后的最优延长保修策略。
目前,有关保修的研究已取得一定的进展,但多以新产品为研究对象。事实上,在全球提倡环境保护和节约成本的背景下,研究具有一定年龄的二手产品的维修问题更具有现实意义。然而,关于二手产品的研究很少[23]。Chattopadhyay等[24]研究了二手产品在免费更换或者按比例保修情况下的期望保修成本模型,但是没有考虑预防维修;Pongpech等[25]研究了在租赁前对设备进行升级,在租赁过程中,对设备进行预防维修以减少设备的故障成本的策略模型,但是此模型中待优化参数较多,且预防维护时间间隔不相等,在实际应用中是不易操作的;Shafiee等[26]研究了对二手产品进行升级的策略模型,但它是从出售方的角度来进行研究的,没有考虑到顾客的费用问题。
针对当前关于二手产品保修的研究较少,且缺乏从顾客视角考虑的问题,本文拟从顾客视角出发,构建年龄在确定区间内变化的二手产品更新延长保修期满的维修策略模型。该模型与其他已有研究的区别在于:(1)引进了二手产品生命周期的概念。二手产品的生命周期开始于一个二手产品的使用,终止于顾客对另一个二手产品购买的完成;(2)考虑了产品的年龄在确定区间内随机变化的情形;(3)以相关优化理论为依据,以维修期长度τ为决策变量,以顾客期望总费用率的值C(τ)最小作为优化目标。得到的期望总费用率的最小值C(τ*)及对应的最优维修期长度τ*,可为顾客进行产品维修决策提供理论依据。
本文的结构如下:第一部分为引言;第二部分为问题及策略描述;第三部分是数学模型;第四部分给出了模型最优化的相关理论及证明;第五部分是算例分析,并对参数的灵敏度进行了研究;最后是总结和展望。
2 问题及策略描述
经销商为了保证所售二手产品的有效运行和增加产品的市场竞争力,通常会在产品出售时,附带有一定的保修期限。二手产品的生命周期可分为三个阶段:(1)基本保修期w。基本保修期可分为两个互不相交的区间:更换保修期(replacement warranty,RW)和小修保修期(minimal repair warranty,MW),其区间长度可分别表示为:[0,θw]和(θw,w]。在更换保修期[0,θw]内,若产品发生故障,将用另外的产品进行更换。同时,产品的保修期将进行更新。在更换保修期内,由产品更换所产生的费用,有两种分摊方式:一种是全部由经销商承担;另一种是由经销商和顾客依据设备已运行的年龄按比例分摊。在产品进行更换时,将会给顾客造成生产相关的损失费用。在小修保修期(θw,w]内,若产品发生故障,则只进行小修;(2)延保期kδ(k≥1)。在基本保修期满后,顾客可以选择购买一定长度的延长保修期δ,当顾客重复购买k(k≥2)次延长保修期时,经销商会给予顾客一定的价格折扣φ,此段时间称之为延保期(extended warranty,EW)。在此期间,设备所产生的故障小修费用均由经销商来承担,顾客只需支付延保费用;(3)维修期τ。当延保期满后,产品的维修费用完全由顾客自己承担,此段时间称为维修期τ。当维修期终止时,顾客将对产品进行更换。图1为更新延长的两阶段保修模型示意图。
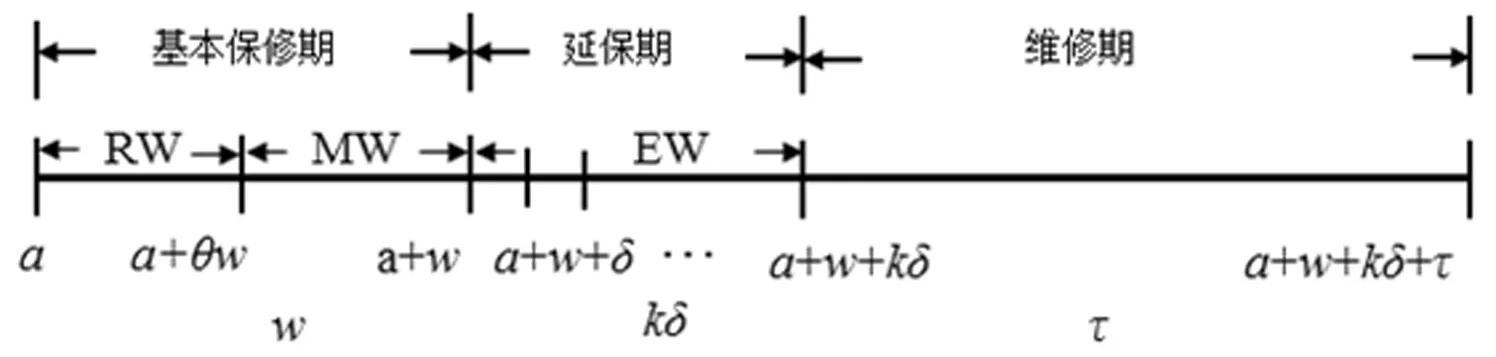
图1 更新延长两阶段保修模型示意图
由于延保期满后,维修期τ内的所有维修费用需由顾客承担。对顾客而言,如何确定最优的维修期τ,使得所购二手产品在整个生命周期内的期望总费用率最低,是其关注的核心问题。因此,本文拟从顾客的角度,综合考虑二手产品在生命周期内三个阶段的费用情况,建立了免费保修策略和按比例保修策略两种策略模型,以二手产品的维修期τ的长度作为决策变量,以整个生命周期内的期望总费用率的值C(τ)最小为优化目标,优化获得最优期望总费用率C(τ*)的值及对应的最优维修期τ*的值,从而为顾客进行产品维修计划提供指导。
3 基本模型
符号注记:
Free replacement/repair warranty(FRRW)免费更换/维修保修
Pro-rata replacement warranty(PRRW)按比例保修
Replacement warranty(RW)更换保修
Minimal repair warranty(MW)小修保修
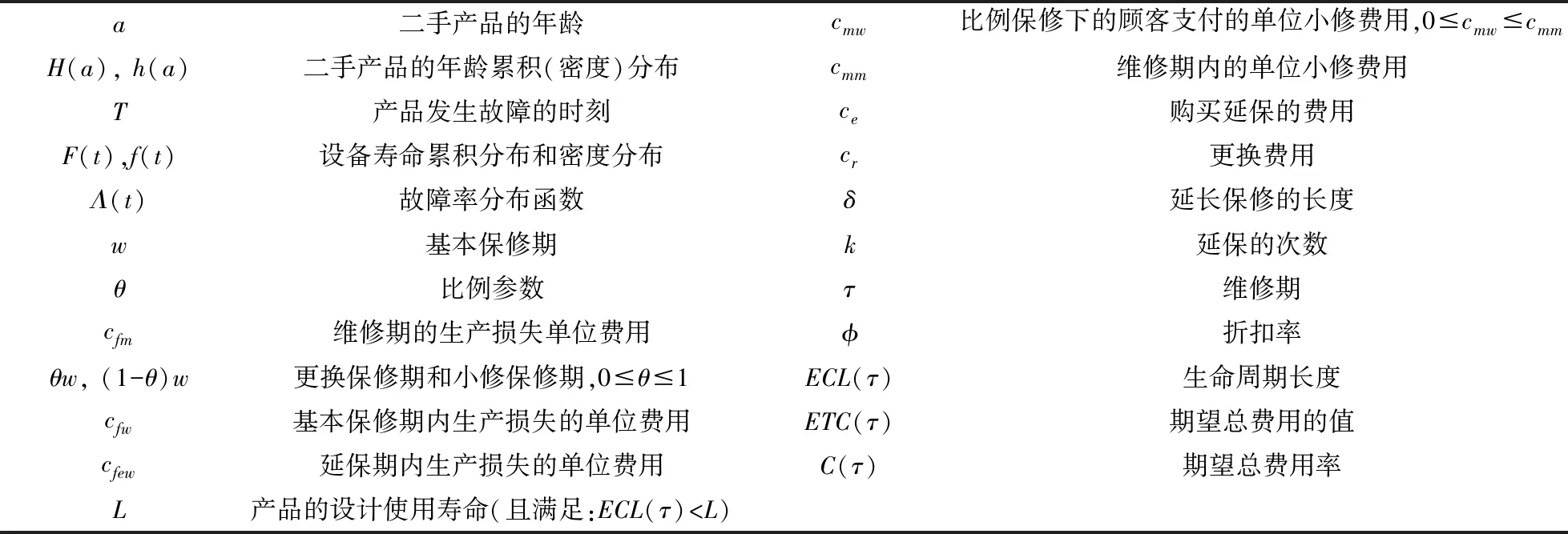
a二手产品的年龄cmw比例保修下的顾客支付的单位小修费用,0⩽cmw⩽cmmH(a), h(a)二手产品的年龄累积(密度)分布cmm维修期内的单位小修费用T产品发生故障的时刻ce购买延保的费用F(t),f(t)设备寿命累积分布和密度分布cr更换费用Λ(t)故障率分布函数δ延长保修的长度w基本保修期k延保的次数θ比例参数τ维修期cfm维修期的生产损失单位费用ϕ折扣率θw, (1-θ)w更换保修期和小修保修期,0⩽θ⩽1ECL(τ)生命周期长度cfw基本保修期内生产损失的单位费用ETC(τ)期望总费用的值cfew延保期内生产损失的单位费用C(τ)期望总费用率L产品的设计使用寿命(且满足:ECL(τ) 模型假设: (1)在基本保修期内,制造商提供的更换保修和小修维修服务的时间忽略不计; (2)在基本保修期和延保期内,二手产品的保修索赔时间忽略不计; (3)在延长保修期和维修期内,小修维修服务的时间忽略不计。 假定产品的寿命服从二参数的Weibull分布:f(t)=λβ(λt)β-1e-(λt)β,则产品的故障率函数分布为: (1) 其中参数λ>0,β>1。 若二手产品的年龄a是随机变量,其累积分布函数和密度函数分别为H(a)和h(a),假定密度函数h(a)的表达式为[27~30]: (2) 则累积分布函数H(a)为: (3) 其中,H(L)=0,H(U)=1。 则二手产品的平均年龄为: (4) (w+kδ+τ) (5) 产品在更换保修期[0,θw]内的故障数服从几何分布: (6) 公式(5)关于N=n求期望,则生命周期的期望值为: (7) 假定CBW,CEW,CM,Cr分别表示基本保修期费用,延保期费用,维修期费用和生命周期终止时的产品更换费用。则顾客期望总费用的值为: ETC(τ)=E(CBW)+E(CEW)+E(CM)+E(Cr) (8) 当系统在更换保修期(RW)内发生N=n次更换时,公式(8)右式中的每项含义如下: (1)基本保修期费用E(CBW)。基本保修期由更换保修期(RW)和小修保修期(MW)两阶段组成,当系统在更换期内发生N=n次更换时,在FRRW策略下,基本保修期费用由两部分构成:第一阶段保修内的生产损失费用和第二阶段保修期内的生产损失费用;而在PRRW策略下,基本保修期费用由四部分构成:更换保修期(RW)内的更换成本分摊、更换时的生产损失费用,小修保修期(MW)内的生产损失费用和需要顾客支付的小修费用。具体如下: (9) (2)延保期(EW)费用E(CEW)。在FRRW和PRRW两种策略下,延保期费用是相同的,为购买延保所支付的费用和延保期间的生产损失费用: (10) (3)维修期费用E(CM)。在FRRW和PRRW两种策略下,维修期费用是相同的,为设备的小修费用和生产损失费用构成: E(CM)=(cmm+cfm)M(τ) (11) (4)更换费用E(Cr)。当维修期满后,顾客将会对产品进行更换。因此,将产生更换费用: E(Cr)=cr (12) 由公式(9)~(12) ,可得当发生N=n次更换时的期望总费用为: (13) 对上述公式(13)关于N=n求期望,则得到期望总费用ETC(τ)的值为: (14) 根据以上分析,综合公式(7)、(14)和文献[27]的相关理论可得,在生命周期内的期望总费用率的值为: (15) (16) 公式(15)中的待优化决策变量为产品的维修期τ。则优化问题即转化为寻找τ*,满足: C(τ*)=min0≤τ<∞C(τ) (17) 为寻找维修期的最优值τ*,令: (18) 将公式(18)展开并整理,得到: =c0/(cmm+cfm) (19) 为证明公式(19)解的唯一性,可以使用函数的伪凸性[1]。若公式(15)具有伪凸性,则仅有一个局部最小值,因此也仅有一个全局最小值存在。给出一个引理: 引理1如果F(x)是一个严格递增的分布函数,则对于给定的k,C(τ)关于τ是伪凸的。 因此,函数Q(τ)是正的且是凸的。又函数ETC(τ)是线性的且是正的,所以函数C(τ)关于τ是伪凸的。 定理1给定k≥1,若F(x)是一个严格递增的分布函数,则: 证明利用伪凸性和公式(19),即可得证。 从定理1可知,满足公式(19)的τ的值,即为最优维修期τ*。此时,对应的C(τ*)的值即为最优期望总费用率。 经销商从市场购得大量二手汽车,经过归类整理,将同一型号且年龄在区间[L,U]上的二手汽车,进行统一制定销售价格。针对二手汽车的关键零部件,制定基本保修、延长保修维修策略。对顾客来说,如何确定最优的维修期τ,使得所购二手产品在整个生命周期内的期望总费用率最低,是其最关心的问题。部分参数的取值如表1所示。 表1 算例中参数的取值 图2 当参数β=2,3,4时,FRRW策略下的曲线图 图3 当参数β=2,3和4时,PRRW策略下的曲线图 图2,3为当其它参数取值不变,参数β分别取2,3和4时的两种维修策略下的顾客期望总费用率的值变化趋势图。图2为免费更换策略下的曲线图,从图中可以看出,当β=2时,期望总费用率的值曲线变化比较平缓,当β=4时,期望总费用率的值曲线变化较陡峭,即当产品的劣化速率加快时,顾客期望总费用率的值变化较大,且期望总费用率的值变大。经计算得出,当参数β=2时,顾客期望总费用率最优值为C(τ*)=1.8779,此时,最优维修期的值τ*=22.9594。当参数β取值为4时,顾客期望总费用率最优值在τ*=8.6960时取得,为C(τ*)=2.7938。通过比较,可以得出结论:当参数β的值增大时,产品劣化的速度加快,顾客期望费用率最优值变大,产品的最优维修期变小。相比较而言,对于顾客来说,购买故障率较高的产品,将要付出更多的维修费用。类似地,可以从图3得出相似的结论。 表2和3为其它参数取值保持不变,参数β更换费用cr和小修费用cmm分别取不同值时,对应的最优期望总费用率的值和最优维修期。从表2和3,可以得出如下结论: (1)当参数β的值增大时,产品的劣化速度加快,两种策略下的最优期望总费用率C(τ*)的值均增大,最优维修期τ*均变小; (2)当更换费用cr的值增大时,两种策略下的最优期望总费用率的值C(τ*)和最优维修期的值τ*均增大; (3)当小修费用Cmm的值增大时,两种策略下的最优期望总费用率的值C(τ*)均增大,最优维修期τ*均变小; (4)FRRW策略下的最优期望总费用率的值均比PRRW策略下的要低。 表2 当参数β,cr和cmm别取不同值时,FRRW策略下的最优值取值情况 表3 当参数β,cr和cmm分别取不同值时,PRRW策略下的最优值取值情况 本文针对二手产品的维修问题, 给出二手产品生命周期的定义,并从顾客的角度,提出考虑更新延长两阶段免费更换保修和按比例更换保修两种策略模型。本文结论可为顾客制定有效的产品维修计划提供了决策的理论依据。如何为二手产品设计合理的二维保修方案,是未来的研究方向。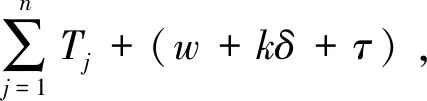

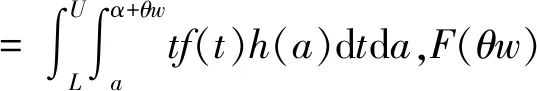
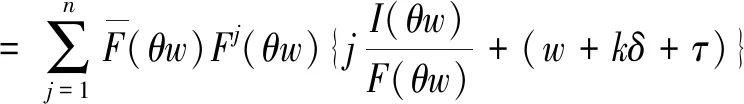

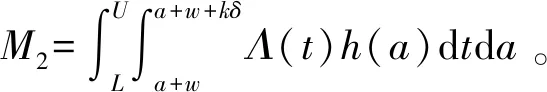
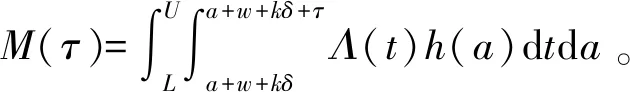
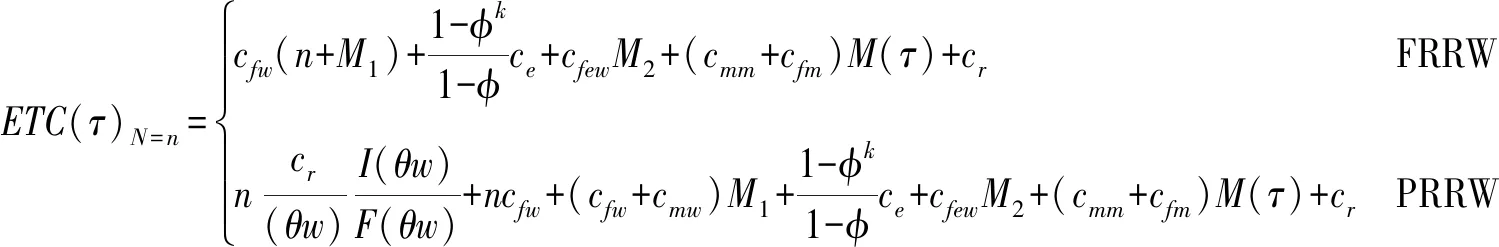
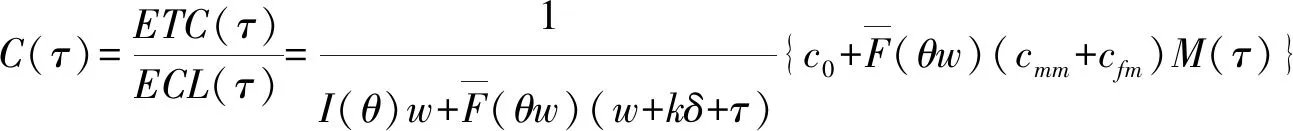
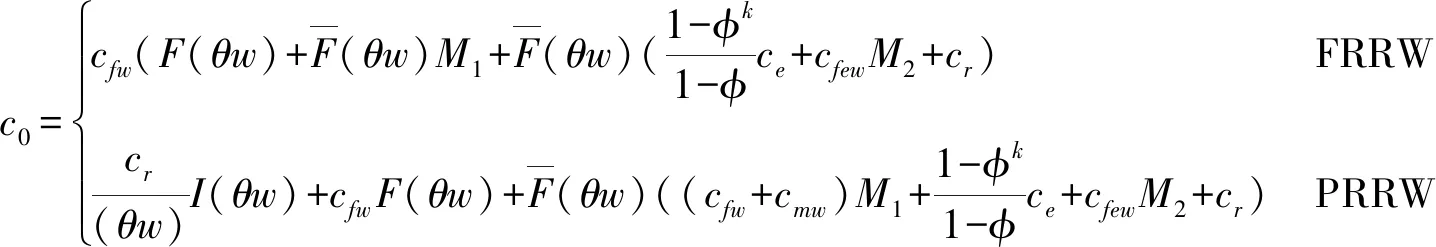
4 模型优化
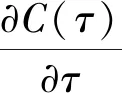
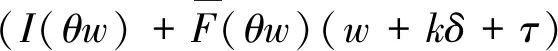
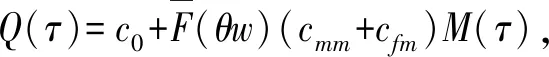
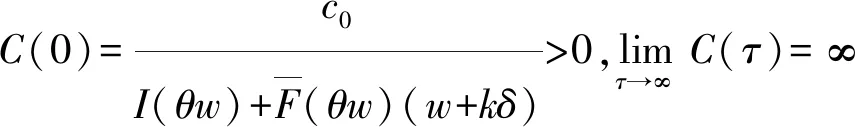
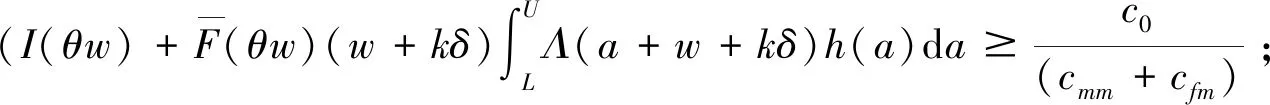
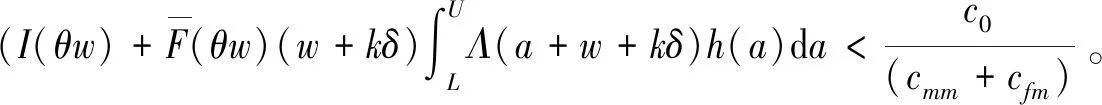
5 算例分析

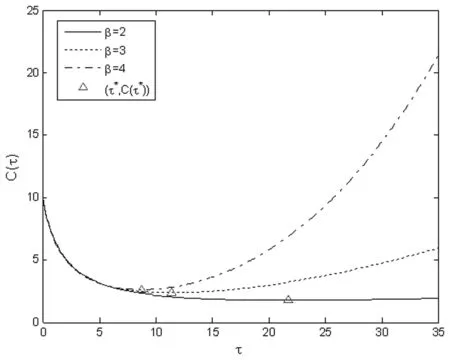
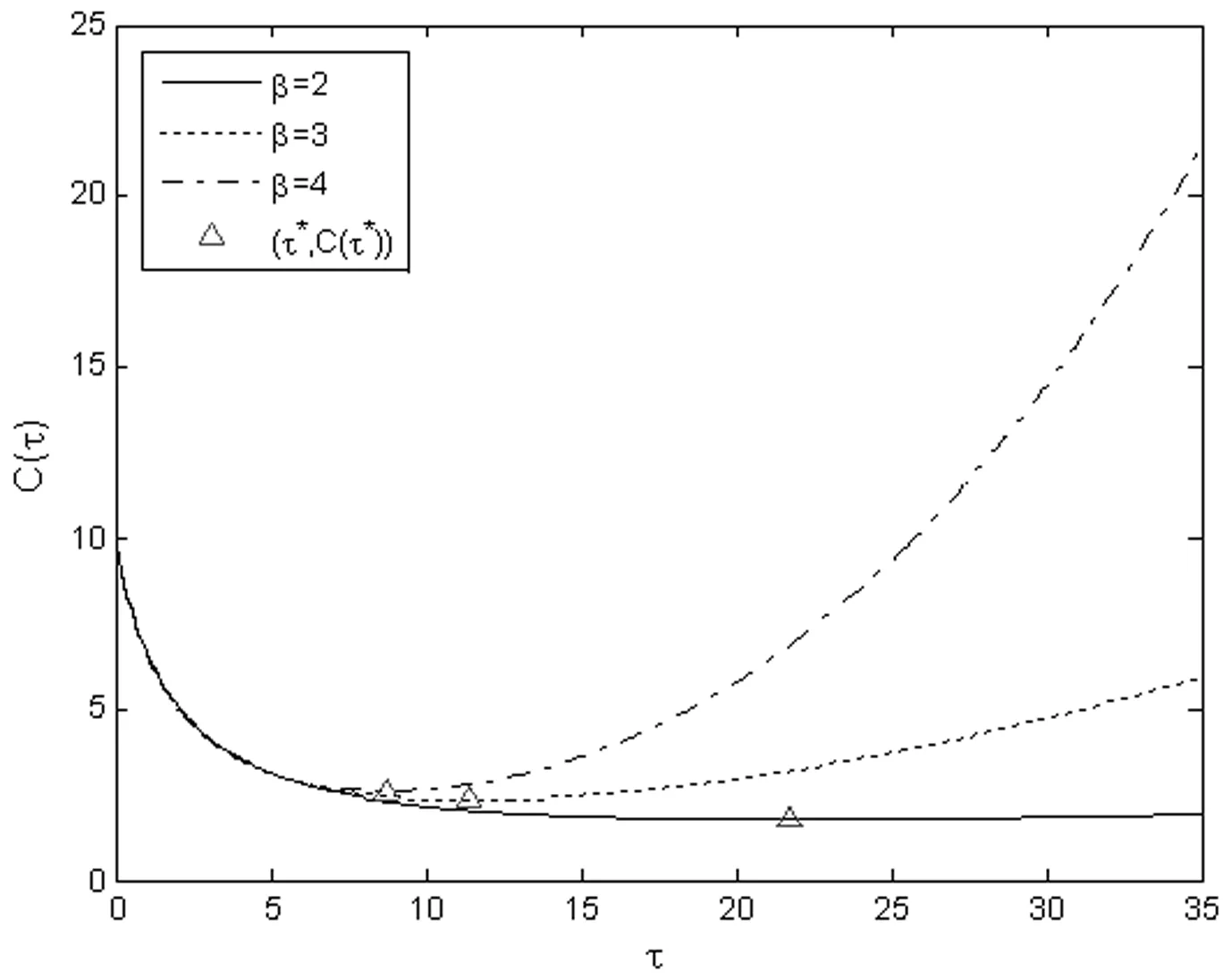
5.1 当参数β取不同值时顾客期望总费用率值的变化情况
5.2 两种策略下的期望总费用率比较
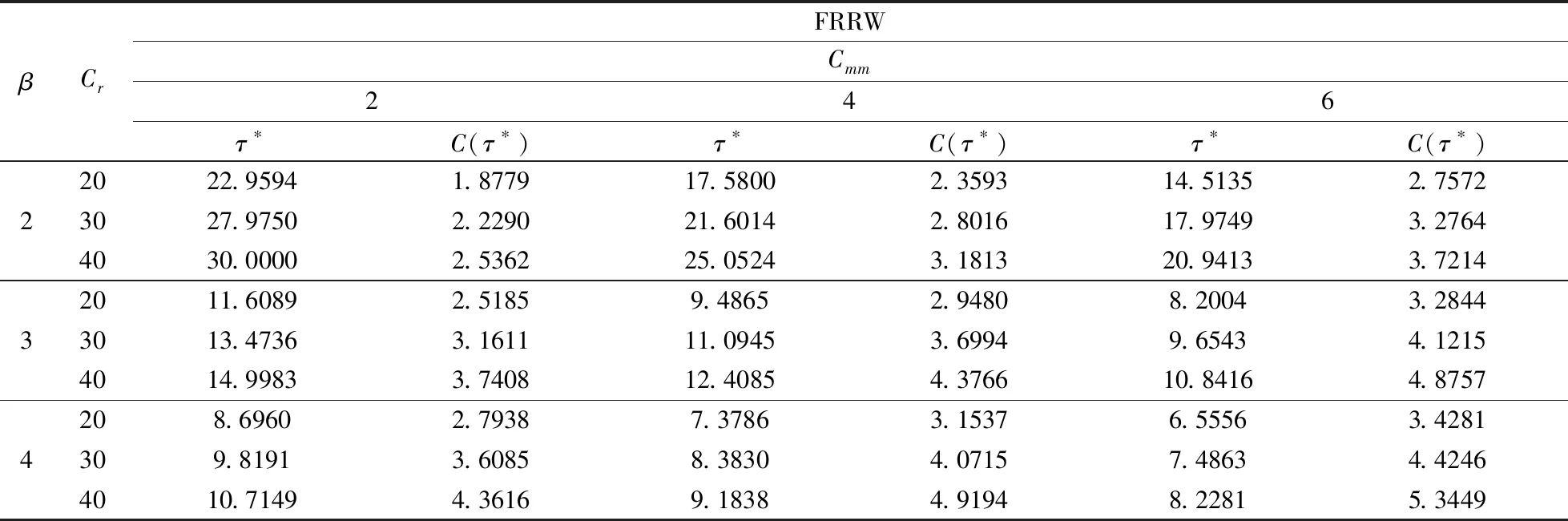
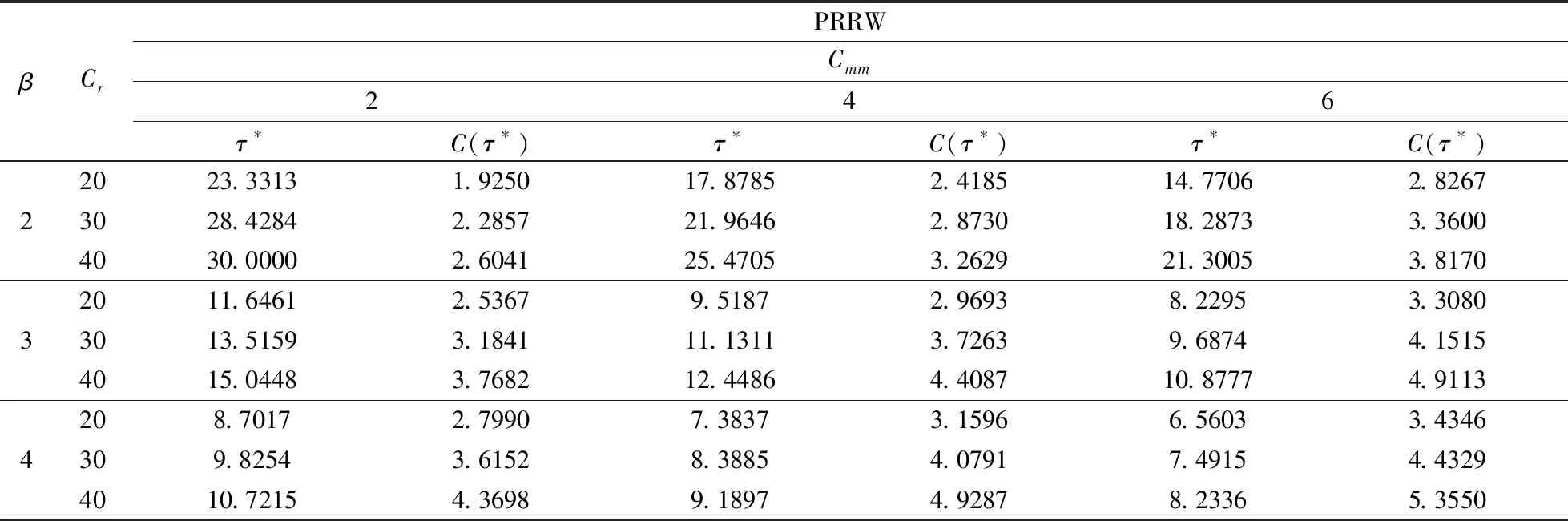
6 结论
