带交互效应的面板SVAR模型的估计

叶小青

(中南民族大学 数学与统计学学院,武汉430074)

面板SVAR模型不仅可测度内生变量间的动态影响机制，还能揭示即期关系，从而广泛应用于经济金融等各领域的动态分析[1,2].例如各省通胀水平波动的动力来源分解、即期冲击和长期冲击的效应等，在对这些经济问题进行分析时，常常发现各省通胀水平还会受到利率、外汇储备等外部因素的共同影响，这些因素是各省共同面对的，只随时间变化，且各省对利率、外汇储备的敏感程度存在差异.而传统的面板SVAR模型无法测度个体对共同影响因素的效应的差异性，因此需要在传统面板SVAR模型中引入时间效应与个体效应的交互项，研究带交互效应的面板SVAR模型就显得尤为必要.

现有文献对面板SVAR模型的理论与应用研究较少，HOLTZ-EAKIN最早将时间序列VAR模型扩展到面板数据模型，给出了基于工具变量的一致性估计量[3].BINDER对短面板VAR提出了差分GMM估计量[4].李娟伟和刚翠翠使用面板SVAR模型，从贸易增长的角度研究了经济发展质量和效益的动态影响机制[5].王小泳等基于1998～2009年1383家上市公司数据，运用面板SVAR模型研究了现金股利、投资效率和公司价值之间的关系[6].兰晓霞运用面板SVAR探讨了信息资源与高技术产业创新的动态关系和协调问题[7].

虽然学术界的相关研究成果对面板SVAR模型的研究进程，具有积极的推动作用，但是就研究内容来看，目前国内外对于面板SVAR模型的理论研究忽略了个体效应和时间效应的交互项，以至于模型存在偏误，动态机制的测度不准确，更无法度量个体对共同社会环境因子的不同效应.如在通胀研究中，各省通货膨胀对利率等货币政策的反应不一样，有必要考虑各省(个体)与利率的交互效应.因此，将面板SVAR和交互效应结合起来，建立带交互效应的面板SVAR模型(IEPSVAR)，不仅可以修正模型设定的偏误，而且能反映个体对社会环境共同因子的效应差异性，并给出一致性估计算法，编制估计程序，讨论有限样本性质，使得基于IEPSVAR模型的应用研究，能更准确地揭示经济关系的动态变化特征.

1 带交互效应的面板SVAR模型的设定

结合交互效应与面板SVAR模型，设定带交互效应的面板SVAR模型为：

Γ0Yi,t=Γ1Yi,t-1+Γ2Yi,t-2+…+ΓpYi,t-p+μi+Ξi,t,

Ξi,t=ΛiFt+ui,t,i=1,2,…,N,t=1,2,…,T,

(1)

其中，Y为r维向量，由内生变量组成.Γ0为即期结构参数矩阵，Γp为滞后系数矩阵，μi为个体效应.ΛiFt为交互项，Λi为因子载荷，Ft为共同因子，u为结构型冲击扰动项，因为模型(1)考虑了各内生变量之间的即期和动态影响，所以结构型冲击u不相关，简记为u～iid(0,Σr×r)，Σ为对角矩阵.带交互效应的面板SVAR模型(1)无法直接估计，需要先将其转化为诱导型模型——带交互效应的面板VAR模型(IEPVAR)：

(2)

令：

(3)

则诱导型模型(2)简化表述为：

Yi,t=H1Yi,t-1+H2Yi,t-2+…+HpYi,t-p+αi+

(4)

其中，Ω为非对角矩阵.模型(4)中每一个单方程都是带交互效应的动态面板数据模型，可通过迭代GMM方法进行估计[8]，然后根据诱导型模型(4)的参数与结构型模型(1)的参数之间的对应关系，实现交互效应面板SVAR模型(1)的估计.

2 带交互效应的面板VAR模型的系数估计

在估计带交互效应的面板SVAR模型(1)之前，需要先估计带交互效应的面板VAR模型(4).为表述方便，此部分考虑最简单的形式，滞后阶p=1，内生变量的个数r=2，因模型(4)每个单方程都是带交互效应的动态面板数据模型，在此仅以第一个方程为例：

y1i,t=β1y1i,t-1+β2y2i,t-1+α1i+ξi,t，ξi,t=λ1if1t+ε1i,t,

(5)

对于带交互效应动态的面板数据模型(5)，由于y1i,t-1和y2i,t-1与共同因子f1t和因子载荷λ1i相关[9]，若直接采用GMM估计，所得估计量是非一致的，因此提出迭代GMM估计方法，其估计思想为：给定β1，β2，α1i情况下，得到因子结构模型为：

(6)

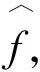
(7)

对式(7)进行差分运算，消除α1i，为Δy1i,t-1,Δy2i,t-1分别选取工具变量{y1i,1,…,y1i,T-2}，{y2i,1,…,y2i,T-2}，构造矩条件，利用差分GMM估计，可得β1，β2，α1i的一致性估计量.

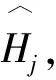
3 带交互效应的面板SVAR模型的参数识别和估计

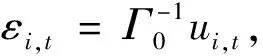
4 带交互效应的面板SVAR模型估计的有限样本性质

4.1 仿真数据生成

设带交互效应的面板SVAR模型生成过程为：

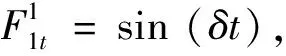
4.2 参数估计量的有限样本性质

4.2.1 参数估计量的偏误和有效性

为了考察带交互效应的面板SVAR模型估计量的偏误和有效性，给出各参数估计量的均值和标准差，结果如表1～表3所示.

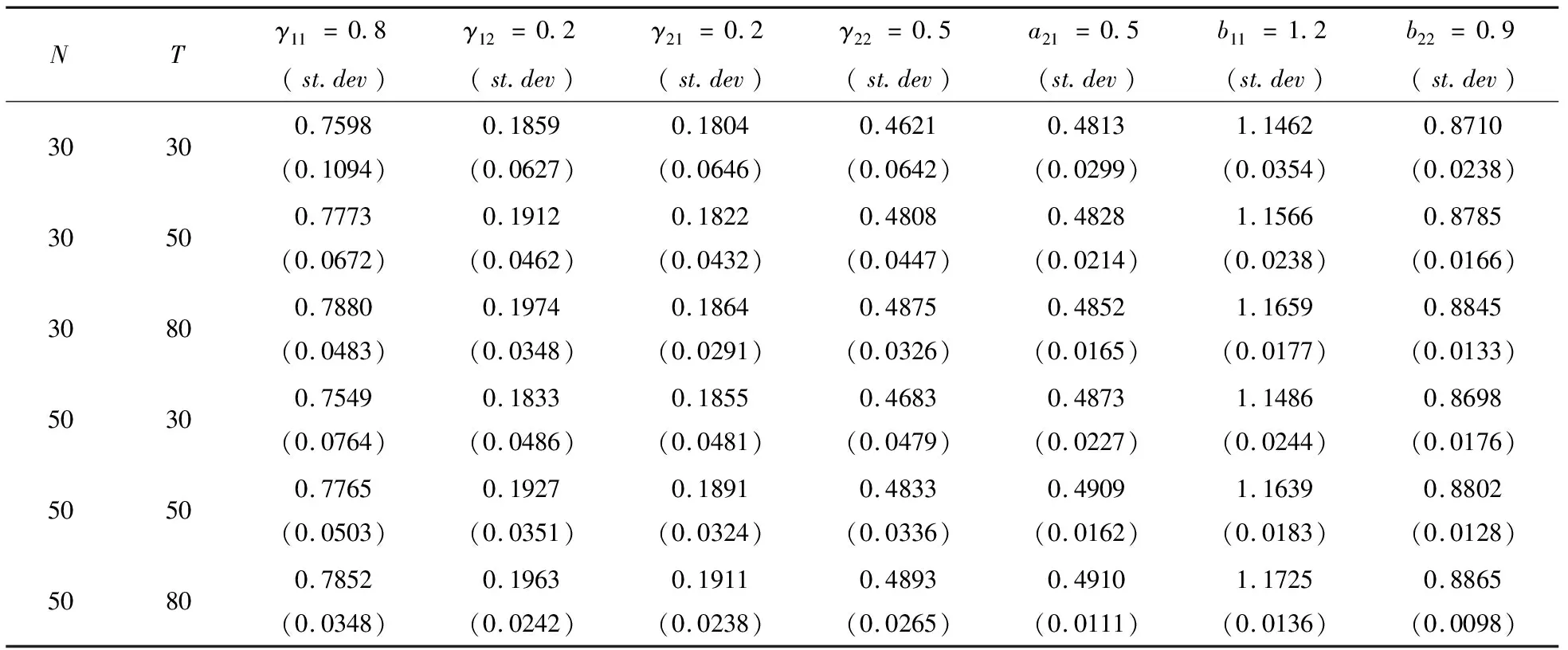
表1 IEPSVAR参数估计结果(周期型因子)

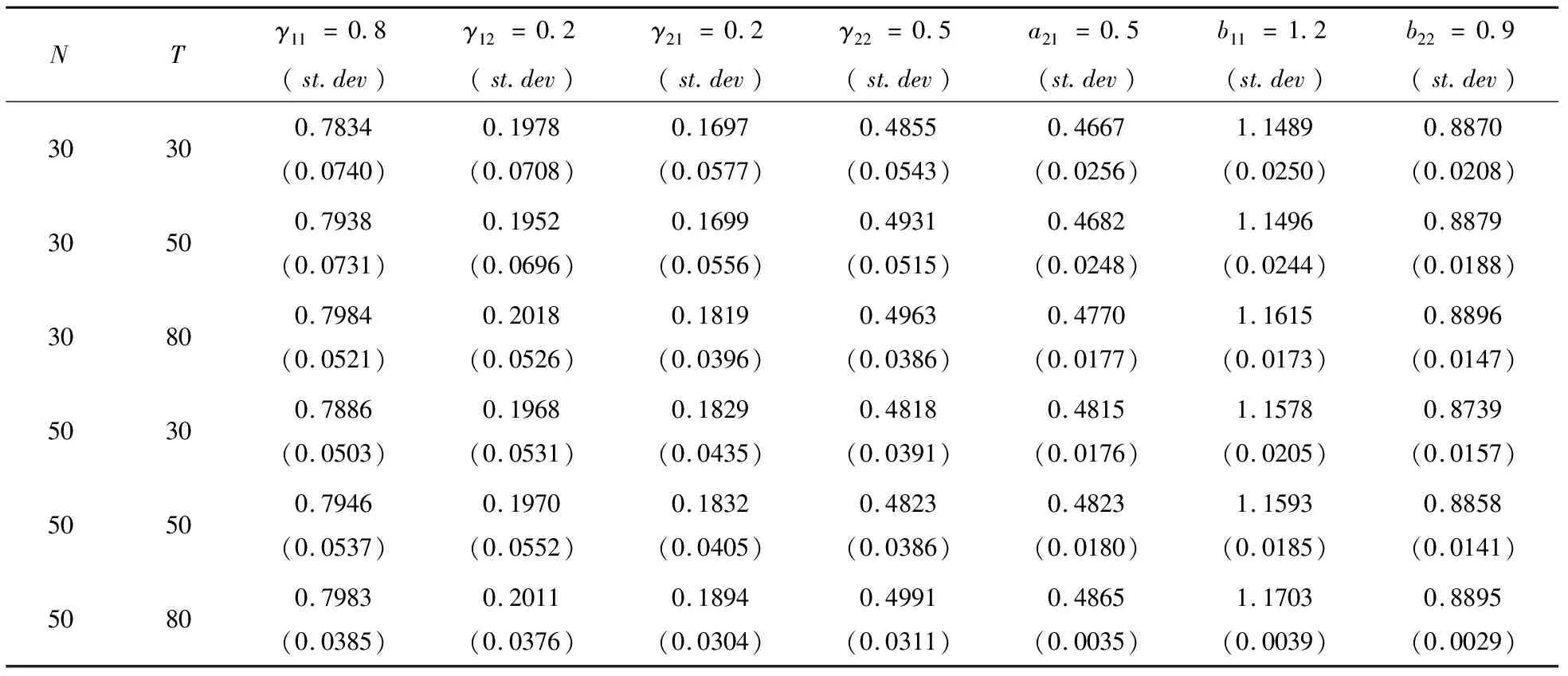
表2 IEPSVAR参数估计结果(阈值型因子)

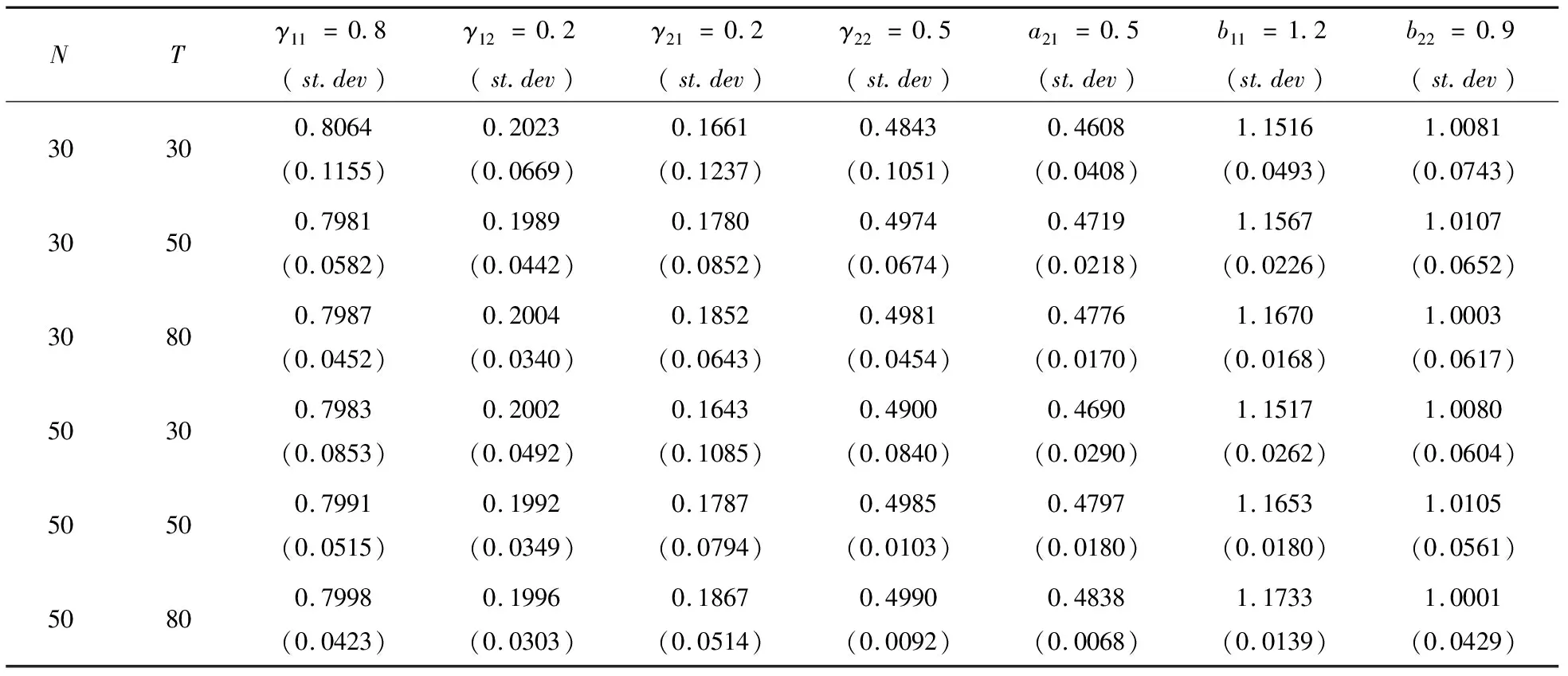
表3 IEPSVAR参数估计结果(随机型因子)

仿真实验结果显示：在3种共同因子的设定方式下，带交互效应的面板SVAR模型参数的估计值都非常接近真值.在给定N(T)的情况下，随着T(N)的增大，估计值和真值的偏差逐渐减小，并趋近于0；并且随着样本容量的不断增大，各估计量标准误均有逐渐减小的趋势，这表明带交互效应的面板SVAR模型的迭代GMM估计方法的有限样本性质表现良好.

4.2.2 因子载荷和共同因子的仿真结果

表4～表6中corrf1和corrf2分别为共同因子F1t,F2t估计值与真值的相关系数，corrlamuda1和corrlamuda2分别测度因子载荷λ1i,λ2i估计值与真值的相关系数，度量估计量与真值的逼近程度.

从表4～表6可以看出，在随机型共同因子设定形式下，共同因子的估计值与真值的相关系数，因子载荷的估计值与真值的相关系数绝大部分达到0.95以上，这说明共同因子和因子载荷都能被准确估计；在周期型共同因子的设定下，共同因子的估计值与真值的相关系数，因子载荷的估计值与真值的相关系数均能达到0.85以上，共同因子和因子载荷的估计值都能代表其真值的绝大部分信息；在阈值型设定下，无论是共同因子还是因子载荷，估计值与真值的相关性都弱于随机型和周期型，相关系数处于0.6～0.9之间.

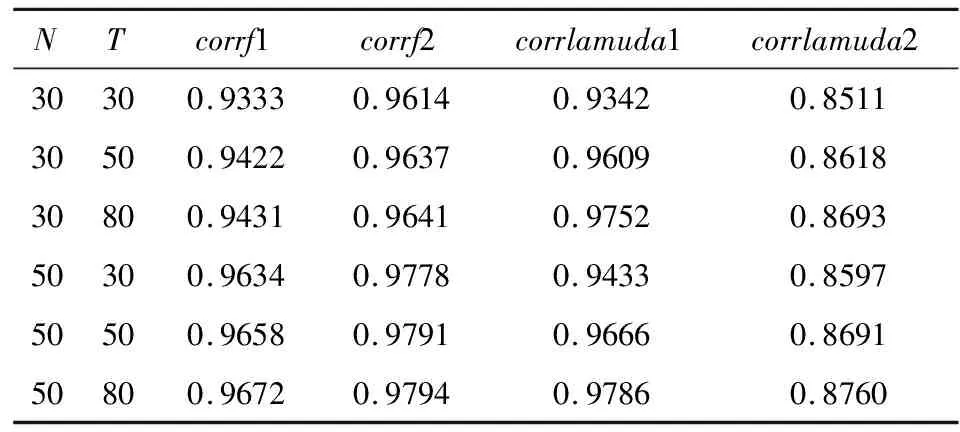
表4 共同因子和因子载荷的估计(周期型因子)

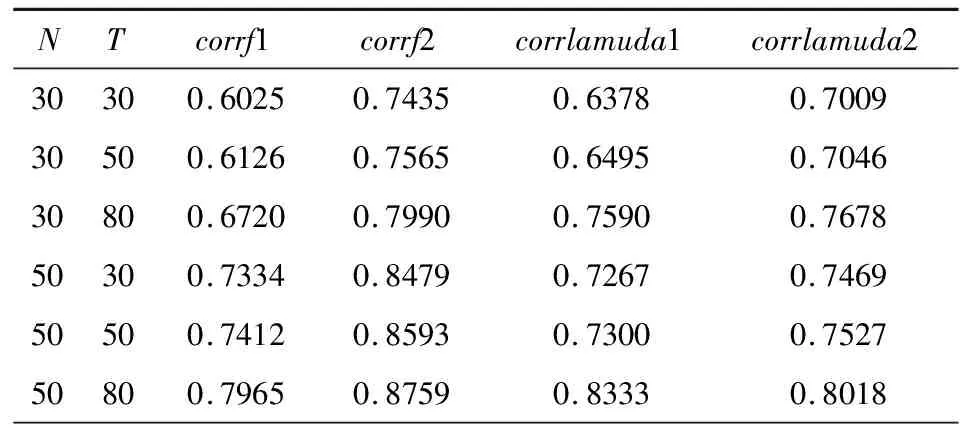
表5 共同因子和因子载荷的估计(阈值型因子)

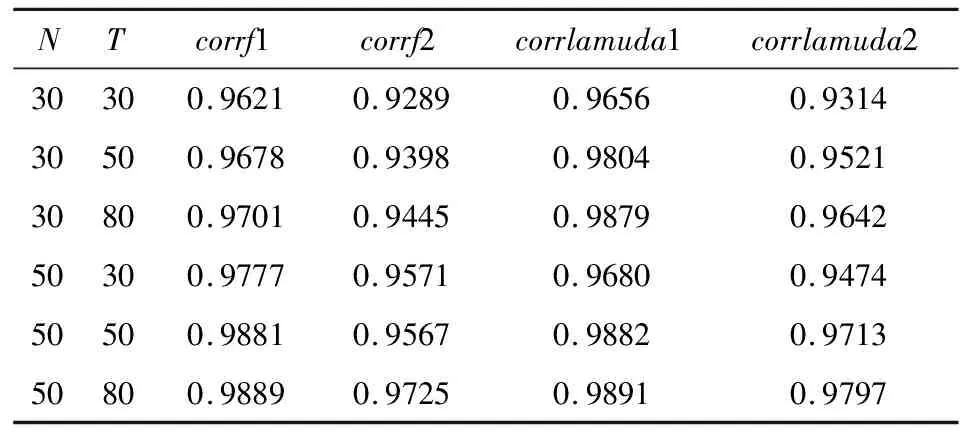
表6 共同因子和因子载荷的估计(随机型因子)

5 结论

带交互效应的面板SVAR模型不仅能够测度经济系统中变量之间的即期和动态关系，而且还可充分发挥交互效应的优点，测度不同个体对共同影响因素的效应的差异性，在宏观经济分析中具有不可忽略的、独特的地位.本文构建了带交互效应的面板SVAR模型，提出一致性估计量，仿真模拟有限样本性质，研究结果表明：在3种共同因子的设定方式下，随着样本容量的增加，参数估计量的偏误和标准误逐渐减小，并趋近于0.在随机型共同因子的设定形式下，共同因子、因子载荷的估计值与真值相关系数达到0.95以上，在周期型共同因子的设定形式下，共同因子、因子载荷的估计值与真值相关系数达到0.85以上.