基于优化ADRC的单臂机器人轨迹跟踪研究

陈 壮，王宪伦，陈 闪

(1.芯恩(青岛)集成电路有限公司，山东 青岛 266000;2.青岛科技大学机电工程学院，山东 青岛 266061;3.青岛滨海学院机电工程学院，山东 青岛 266555)

0 引言

机器人抓取物体的工作看似简单，实际上是多耦合的非线性轨迹解算过程[1]。对于机器人末端执行器的轨迹规划，一般将末端执行器的笛卡尔坐标系由运动学算法映射到关节空间中，解算并拟合得到理想的抓取角位移轨迹和角加速度，将关节变量转换成脉冲值发送给伺服电机完成各轴的协同动作。但是实际上机器人常处于微振动的环境中，不可避免地受到自身共振和地面振动的不确定挠动，导致抓取轨迹与拟合的轨迹偏离。为了使机器人高精度跟踪抓取轨迹，需要在已知机器人的运动学和动力学模型的前提下构造轨迹跟踪控制系统。

Yu等[2]为了减轻内外部的干扰耦合对无人直升机螺旋桨操控的影响，建立了ADRC自抗挠模型，对比PID控制算法，提高了系统的动态稳定性。Wang等[3]将自抗挠模型应用于交流电，估计逆变器的周期性负载扰动。廖薇等[4]构造了ADRC模型使得海洋绞车适用于不同线缆直径和重量的工况，即使当环境变化时，控制器也能保持良好的动态性能，对比了PID控制器，证明了ADRC有较快的响应速度和抗干扰能力。

自抗扰控制(ADRC)算法是在PID控制理论基础上延伸发展而来的[5]，能自主抵抗机器人内外部的各类干扰，具备高精度的轨迹跟踪能力，并且其关键参数也可以根据实际跟踪能力进一步优化。

1 关节空间动力学模型

实验用的是加拿大Kinova公司研发的MICO2仿人六轴串联机器人，在关节空间下对应位置和时间的拉格朗日动力学方程的一般形式为

(1)

(2)

(3)

2 建立ADRC模型

标准二阶ADRC由微分跟踪器(TD)、非线性状态误差反馈(NLSEF)和扩张状态观测器(ESO)独立的3部分组成，如图1所示。变量q为机器人各关节轴输出的角位移，设定变量qc为机器人关节拟合轨迹的任意位置，变量qc1为输入轨迹qc的跟踪信号，qc2为输入轨迹qc微分后速度的跟踪信号，它们由ESO实时提取跟踪值qc1和qc2，从而确保跟踪值的稳定性。κ为系统内外的不确定干扰；τ为考虑内外干扰引入的系统补偿量。

图1 二阶ADRC框架模型

跟踪值qc1和qc2的二阶非线性跟踪微分器TD函数形式为

(4)

k=fh(qc1-q，qc2,r0,μ),r为跟踪速度控制因子，一般|k|≤r；r0为r的整数倍，一般按实际控制需求选择合适的倍数；h为轨迹采样周期，μ为噪声滤波控制因子，一般为h的20倍；fh为控制反馈跟踪函数。

ESO是自抗扰控制器的核心，用于跟踪变量，估计并补偿不确定挠动以消除系统噪声，这也是PID没有的功能。设变量z1为qc1的估计值，变量z2为qc2的估计值，变量z3为扩张变态变量。β1、β2、β3为ESO内部参数，构建ESO算法为

(5)

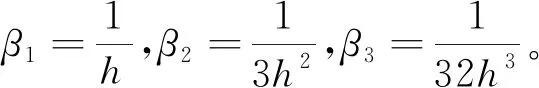
至此，已经通过ESO估计了机器人内外不确定挠动，为了使挠动的抵消变得可控，引入非线性状态误差反馈(NLSEF)。NLSEF是自抗扰控制器特有的组成部分，流程如图2所示，用于调整增益限制系统挠动，调节速度在较小的范围内波动从而避免超调。已知TD跟踪得到的角位移qc1和速度qc2，以及ESO得到轨迹估计值z1和速度估计值z2。对应数值做差法运算得到跟踪误差e1和e2。结合控制反馈跟踪函数fh，得到NLSEF表达式为

(6)

c为阻尼系数。

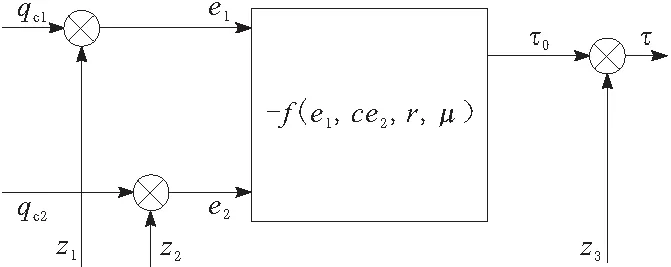
图2 NLSEF计算流程

3 轨迹跟踪仿真

外部干扰对轨迹的影响，主要体现在末端执行器角位移变量的瞬时幅值存在噪声且角加速度响应延迟[6-7]。选择Kinova MICO2的第3关节轴跟踪已规划的关节角位移变量q为例，验证二阶ADRC设计的可行性。ADRC跟踪结果如图3所示。由图3可知，当存在干扰时，第3关节轴反馈的实际关节角位移受噪声干扰的影响较明显，明显偏离理想的规划轨迹，而经过ADRC估计并补偿扰动后使得跟踪控制的角位移能够近似向规划的轨迹趋近。

图3 第3关节关节角位移轨迹

4 ADRC参数优化

ADRC算法在运算效率和跟踪干扰等方面都优于PID算法，甚至不依赖于数学模型。各部分参数的优化起着至关重要的作用。考虑到闭环系统的动态特性，为了避免因数据量较大而造成误差信号时滞现象，需要根据误差补偿值动态微调ESO的内部参数β1、β2、β3以及NLSEF的参数kp。参数kp的选取影响着目标值跟踪精度，过大会出现超调现象，因此需要从非线性控制率层面抑制系统超调，减小振荡。

进一步解算kp的最优解，设计了一种基于遗传算法优化径向基网络算法(GA-RBF)实时优化ADRC。RBF神经网络能精准快速逼近设定值，同时由遗传算法(GA)的强鲁棒性并行搜索优化径向基函数(RBF)的网络权值并避免局部极小值，尽可能完善RBF神经网络[8-9]。RBF高斯逼近激活函数为

(7)

隐含层激活函数φ(‖x-ui‖)一般为

φ(‖x-ui‖)=exp(-‖x-ui‖2/σ2)

(8)

‖x-ui‖为基函数与输入矩阵的差向量；g矩阵为权值；σ为函数宽度阈值参数，影响RBF径向范围；p为神经元数量；ui为第i个节点的聚类中心。

通常采用GA并行全局搜索RBF的最优解。GA优化RBF网络的权值流程如图4所示。设定二进制编码，迭代种群规模为N，借鉴生物繁殖理念，选择过程则以评价染色体的方式择优交叉组合产生新的后代，交叉概率和变异概率则跟随适应度改变。当满足迭代阈值时，停止迭代并输出此时种群中最大适应度的个体作为最优权值。网络权值预测数值变化情况如图5所示。

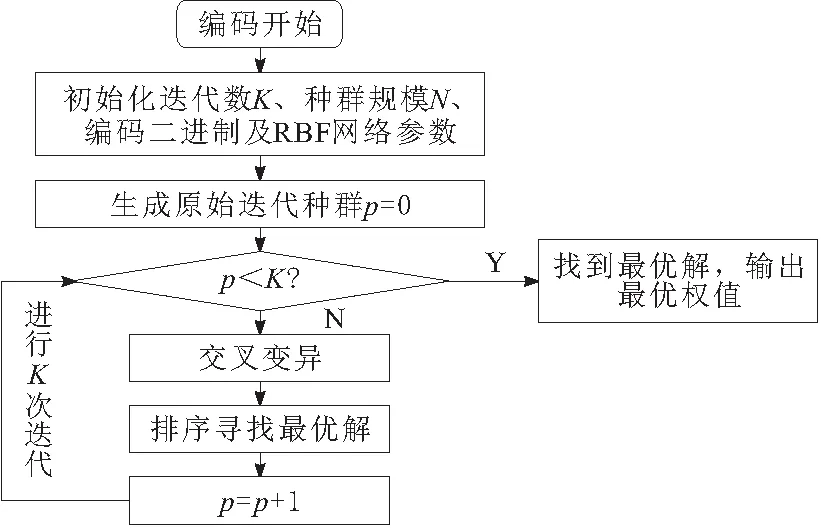
图4 GA优化RBF网络的权值流程

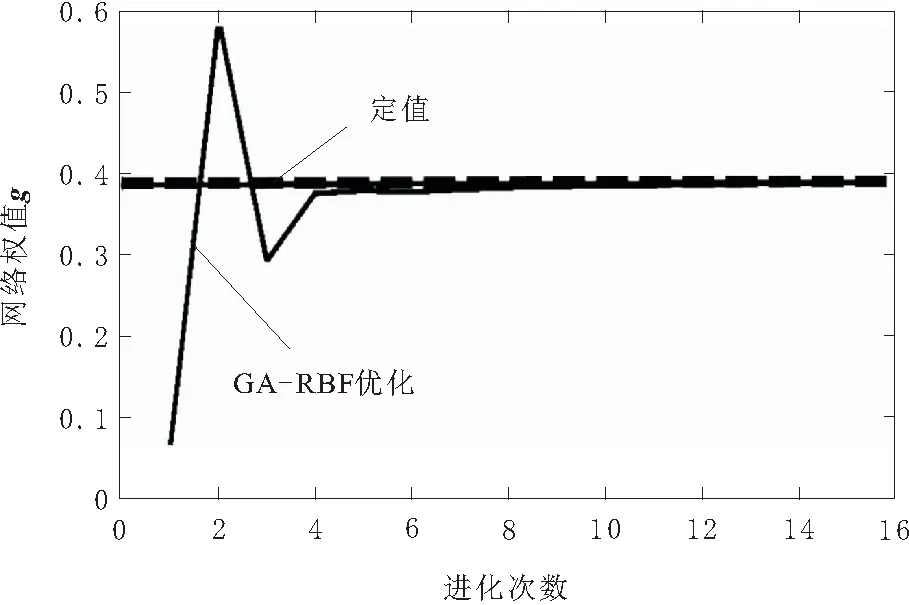
图5 网络权值预测数值变化

由图5可知，在迭代初期，RBF的网络权值g有较大的波动，使得预测值不可靠，随着迭代进化次数的增加使得权值预测值逐步趋于稳定。这也意味着GA预测的最小误差也跟随迭代进化次数的增加逐步收敛至0。使得在当前ADRC跟踪模型下，预测了合适的RBF网络权值g，通过RBF网络优化了NLSEF，微调参数kp，最终实现更高的逼近精度。

5 实验误差分析

第3关节角位移变量q由GA-RBF优化后的ADRC跟踪结果与规划轨迹作差，得到绝对误差偏移量δ，如图6所示。通过偏移幅值清楚地看出该关节的各离散点的跟踪误差临界波动较小，角位移绝对误差偏移量δ基本上能控制在-0.25～0.25 rad范围内，且误差可控。从而将算法映射到机器人的6个关节轴，各轴协同工作使得机器人末端执行器实时跟随已规划的轨迹工作。

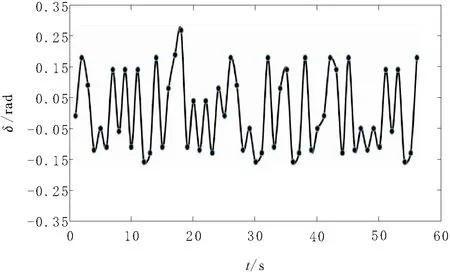
图6 ADRC跟踪误差

6 结束语

机器人普遍存在来自内外界的不确定性干扰，为了使得机器人更好地遵循规划好的轨迹运行。本文以Kinova MICO2为例，在关节空间下建立了ADRC关节角位移跟踪模型。为了确保ADRC适用于各类复杂环境，保证其闭环误差跟踪稳定性。建立GA-RBF网络进一步优化了NLSEF参数kp，控制角位移跟踪误差在一定时间内稳定在可接受的范围内，表明GA-RBF优化的ADRC使机器人实际工作轨迹向着规划轨迹收敛。