双轮式抛投机器人仿富勒烯轮毂结构设计
2020-10-22董洋洋左堃罡韩少杰张子建
董洋洋,左堃罡,韩少杰,张子建
(南京航空航天大学航天学院,江苏 南京 210016)
0 引言
双轮式抛投机器人因其体积小、结构紧凑、运动能力强等特性,广泛应用于探测与救援领域,然而由于工况需要常导致其轮毂发生高冲击过载。常见的抛投式双轮机器人轮毂形式为轮辐式、整球壳式及条幅式等,卡内基梅隆大学的Halloran等[1]设计了一种能承受高冲击载荷的两轮移动机器人 ,采用轮辐式轮毂形式,结构简单、成本低,同时配备悬架系统能够有效吸收冲击的能量;Teeranoot等[2]设计并开发了一种基于柔性件的条幅式轮毂减震机器人,腿的刚度不仅是满足行走需求,同时具有一定的缓冲效果,减小冲击过程中的冲击载荷;北航研发了一种新型的可变结构微型抛掷机器人的机械设计方案[3-4],其轮毂形式采用整球壳式结构,当机器人下落时候保持球形,保证良好的冲击状态;北京理工大学设计了一种双轮式抛掷式半自主侦察机器人[5-6],在与地面冲击时利用橡胶轮胎的弹性形变进行缓冲吸能,并通过有限元仿真分析和冲击实验证明该机器人具有良好的抗冲击能力。
双轮式抛投机器人轮毂的承载能力对于机器人的安全性十分重要,由于抛投机器人在抛投坠落过程中无姿态控制,因此与地面碰撞方向存在随机性,采用球形轮毂以确保与地面撞击接触时各向的同一;抛投机器人的接触力大小与撞击速度以及机器人整体质量有关,因此轮毂的设计采用多孔结构可以有效降低轮毂质量及刚度,在冲击过程中轮毂具有较大形变能力,增大冲击缓冲距离以得到更好的缓冲性能。C60分子是一种由60个碳原子构成的分子,具有较好的力学性能及空间稳定性[7],它为本文新型双轮式抛投机器人轮毂设计提供了思路。
本文基于C60结构的承载优势,设计双轮式抛投机器人的轮毂结构的最优参数,同时根据结构载荷分布情况,以张拉结构为载荷分布优化单元对C60结构载荷分布进行优化,在实现双轮式抛投机器人的轮毂结构功能的基础上改善其力学性能,提高结构强度和稳定性。
1 C60模型建立
C60分子具有较好的力学性能及空间稳定性,根据C60的空间In对称性可对C60分子结构进行数学建模[8]。
取正二十面体体心为坐标原点O,坐标轴z为正二十面体的一个五重轴,且过点F及F1;取与F和F1相邻的顶点分别为A、B、C、D、E和A1、B1、C1、D1、E1;取x轴与AF棱在同一平面,即AF棱在xOz平面上,同时取A点坐标为[a,0,c];并根据x轴和z轴确定y轴方向,坐标系如图1所示。
根据正二十面体与C60的几何特点可得到
(1)

图1 C60分子个点坐标计算示意
R为正二十面体外包络球半径,由于z轴是正二十面体的五重轴,因此绕z轴对A进行旋转操作On,可得与A等价的4个点B,C,D,E的坐标值为:
(2)
(3)
根据正二十面体的结构特点,利用空间反演法得到
(4)
刘红等[9-10]在C60分子中原子坐标的计算中引入调节参数λ并定义λ=截去棱长/原棱长。截去A、F、B3个角,在AF棱上得到2个顶点,在AB棱上得到2个顶点,AD1和BD1上各得到1个点,其坐标向量表示为
(5)
绕z轴按On进行旋转,则可得到30个节点坐标,剩余30个点坐标根据空间反演法获得。同时根据C60结构形式,将棱按其几何特征按已定坐标系由上至下分为13层进行表示,以xOz平面为基准面,逆时针标定棱长标号分别为1,2,3,…,n,则可得到13层杆件编号。
2 C60框架结构静力学分析
2.1 C60框架刚度矩阵建立
C60框架结构的结构强度及整体刚度与其调节参数λ有关,为了得到其强度及刚度与调节参数λ的关系,将C60框架结构模型看作是一种刚架结构,利用刚度及阵法计算各杆件的最大等效力及整体结构的力-位移曲线。本文对C60框架结构性能的研究针对外载荷指向结构几何中心,分别作用于五边形节点和六边形节点2种情况下进行,如图2所示。空间刚架单元每个节点具有6个自由度(ux,uy,uz,θx,θy,θz),对于有n个节点的刚架结构,则其整体刚度矩阵K为6n×6n的矩阵。由图2可知,C60框架结构具有60个节点,因此该结构的整体刚度矩阵K为360×360。
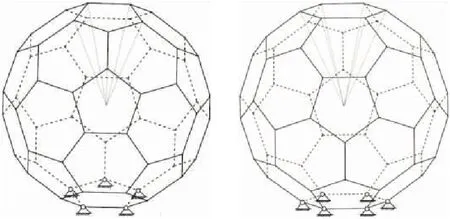
图2 C60刚架结构模型及约束
2.1.1 单元刚度矩阵建立
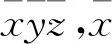
(6)
坐标转换矩阵为:
(7)
(8)
矩阵r的9个元素分别为局部坐标系坐标轴与整体坐标系坐标轴之间的夹角余弦值[12]。利用坐标转换,则可将杆单元在局部坐标系下的单元刚度矩阵转化为整体坐标系下的单元刚度矩阵,即
(9)
2.1.2 C60框架整体刚度矩阵构造
(10)
由式(10)C60结构的整体刚度矩阵,计算节点受力与节点位移之间的关系为
K360×360Δ360×1=P360×1
(11)
Δ360×1为节点位移;P360×1为节点外力矩阵。K360×360一般为奇异矩阵,考虑刚体模型实际约束情况,对于编号为i的固定支座约束,采用主对角元置1法,同时将总刚度矩阵K360×360中第6i~6i-5行及列的元素置0[16]。
2.2 杆的内力分析
对C60框架中杆件内力及节点受力进行分析为
(12)
其中uij中的向量参数可由式(11)解得Δ中的参数取得,从而得到节点受力的大小。根据Von.Mises准则,假设C60刚架结构中所有杆件单元均为理想单元,当忽略杆件单元的弯曲及扭转影响时,对于节点等效应力则确定为
(13)
σ和τ分别为杆件所受拉应力及剪应力,同时根据之前假设,其杆件单元为理想杆件,杆件截面处应力处处相等,则对式(13)左右两端同乘单元截面积则可得到杆单元节点等效力表达式为
(14)
3 结构载荷优化及仿真
3.1 最优截取比例λ
由于截取比例对C60刚架结构的整体受力影响较大,因此针对正二十面体截取比例λ对C60刚架结构的承载能力影响进行分析,以HP3DHR-PA12尼龙为例,建立C60刚架结构的MATLAB数学模型,设置材料参数:E=1 800 MPa;G=643 MPa;μ=0.4;ρ=1.15 g/cm3;正二十面体外接球半径R=200 mm;杆件单元截面为圆,截面半径r=3 mm;载荷P=30 N,指向结构几何中心。仿真分析结果如图3所示,在上述仿真条件的基础上同时分析研究C60刚架结构刚度与截取比例之间的关系,如图4所示。
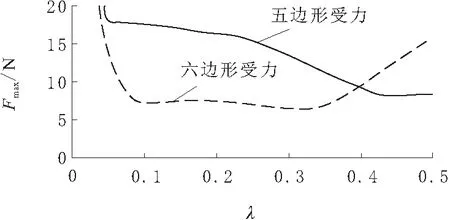
图3 λ对整体结构受等效力最大值Fmax影响
由图3可知:C60在五边形受力时,杆件单元等效力随λ增大逐渐减小,而六边形受力时杆件单元等效力随λ先减后增,当λ在0.100至0.350之间几乎恒定,且2条曲线相交于λ=0.395。

图4 截取比例λ对F-s曲线影响
由图4可看出:当五边形受力时,C60刚架结构的F-s曲线在λ=0.300处整体刚度最小;六边形受力时,C60刚架结构的F-s曲线在λ=0.350处整体刚度最小。由于C60刚架整体刚度近似呈定刚度趋势,因此在计算中可由K=F/s近似计算C60刚架整体刚度。截取比例λ对结构整体刚度影响情况如图5所示。

图5 截取比例λ对结构整体刚度影响
由图5可分析,当截取比例λ取0~0.150时,C60刚架结构整体刚度呈指数级递减,λ变化对结构整体刚度影响较大;当截取比例λ取0.150~0.450时,其对结构整体刚度几乎无影响;而当截取比例λ取0.450~0.500时,其刚度呈递增趋势。根据结构功能要求,抛投机器人在冲击过程中其轮毂需具有较高强度,同时还需满足较小刚度,对比分析图3~图5,当截取比例λ=0.395时,其C60钢架结构的整体承载能力最好,同时整体结构刚度较低。
3.2 C60框架外载荷分布优化
抛投机器人在与地面发生撞击时,其轮毂与轮胎之间的接触方式一般有3种情况:轮毂某一节点与轮胎之间接触挤压;轮毂某条棱(某两节点)与轮胎之间接触挤压;轮毂某一多边形所有棱(所有节点)与轮胎之间挤压接触。在最优λ取值下,对以上3种情况进行分析。当截取比例λ=0.395时,对五边形和六边形轮毂与轮胎之间的3种接触方式不同截荷分布条件下C60刚架受力散点情况如图6所示。

图6 最优截取比例下不同载荷分布条件下
对比图6a、图6b和图6c可知,当载荷分布于五边形单个节点时,其杆件单元等效力最大值为22.7 N,载荷分布于五边形某2个节点时,杆件单元等效力最大值为15.2 N,载荷均布于五边形5个节点时,其载荷最大值为8 N,同时载荷均布于五边形5个节点时相对于其他两种情况,各杆件单元等效力分布较为均匀,因此结构整体承载能力较前两者有较大提升;对比图6d、图6e和图6f,其载荷分布状况与五边形承载相似,当载荷均布于六边形6个节点时,其杆件单元最大值为9.4 N,相对于其他2种承载方式,杆件单元等效力最大值较小,同时各杆件单元等效力分布均匀,具有较好的承载能力。
根据图7所示的ABAQUS仿真应力云图可知,较单点或2点受力情况,载荷均布于五边形或六边形所有节点的应力云图具有较好的对称性,受力均匀,结构稳定性好,同时根据图8对比最优截取比例下C60刚架结构ABAQUS与MATLAB仿真结果基本一致,可证明理论计算的可靠性与正确性,由于MATLAB与ABAQUS仿真在节点处理方式上有所不同,MATLAB中节点为理想刚性节点,不具备材料参数,而ABAQUS建模中对节点进行材料填充,致使两者F-s图之间存在微小误差。
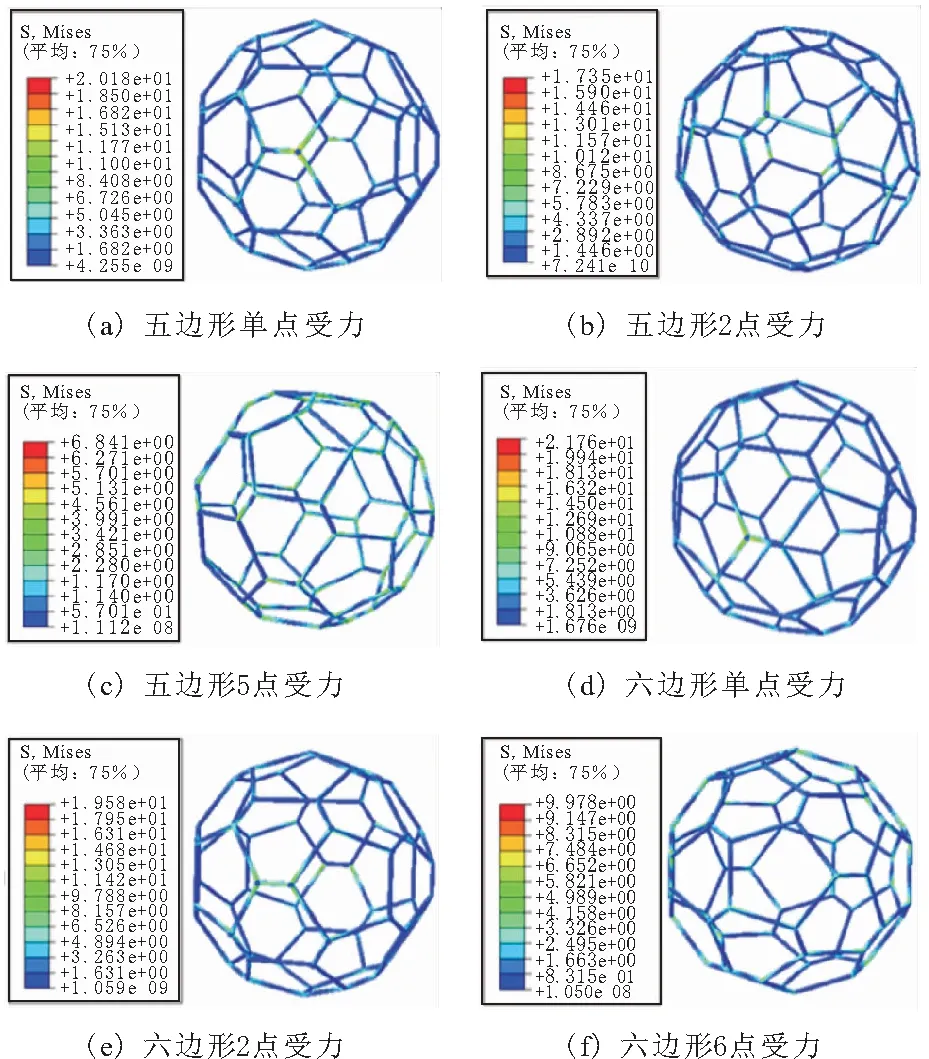
图7 最优截取比例下不同载荷分布条件下C60刚架ABAQUS仿真应力云图

图8 C60刚架结构ABAQUS与MATLAB仿真F-s对比
3.3 C60张拉轮毂横向对比仿真分析
为了改善富勒烯框架结构的受力条件,同时根据图7及图8的仿真结果,本文提出在轮毂框架结构孔洞处设计张拉结构,结构简单,其张拉形式具有较好的承载与散力性能,同时在张拉中心节点上可放置阻尼块,将轮毂与轮胎之间的挤压力转换为沿张拉绳方向的拉伸力,可将作用于阻尼块上的作用力有效地均匀分配在C60框架多边形节点上,其结构示意如图9所示。

图9 张拉结构承载示意
本文对比同外轮廓体积、同质量、不同形式的轮毂,并进行力学仿真分析,仿真模型如图10所示。仿真条件:外轮廓直径D=350 mm;轮毂材料为HP3DHR-PA12高性能尼龙;轮毂质量m=135 g;载荷大小P=30 N,载荷方向取轮毂轴向及侧向。

图10 不同轮毂形式相同条件下模型对比
不同轮毂形式轴向承载ABAQUS仿真应力云图如图11所示。不同轮毂形式轴向承载F-s曲线如图12所示。
由图11及图12可知:轮辐式轮毂结构轴向刚度小,变形量大,对冲击方向性要求较高;条幅式轮毂,具有较好的轴向承载性能,受力易变形,有利于冲击过程中的变形缓冲,但在受侧向力作用时由于结构限制,整体稳定性较差;球壳式轮毂整体承载能力相对较差,应力较为集中,不利于结构的整体承载,同时其刚度相对于其他3种较大,易使得冲击过程中抛投机器人内部机械结构及电子器件过载过大而失效; 相对于上述3种轮毂承载的力学特点,本文提出的仿C60张拉结构轮毂具有较好的强度及刚度特性,整体承载性能较优,轴向承载最大等效应力σa,max=6.23 MPa,侧向承载最大等效应力σl,max=8.68 MPa,张拉形式具有较好的承载与散力特性,应力分布较为均匀,同时具有较好的承载全向性,结构受力整体性好且不易失稳。综合考虑刚度及强度要求,本文提出的仿C60张拉结构轮毂具有较好的实用性。
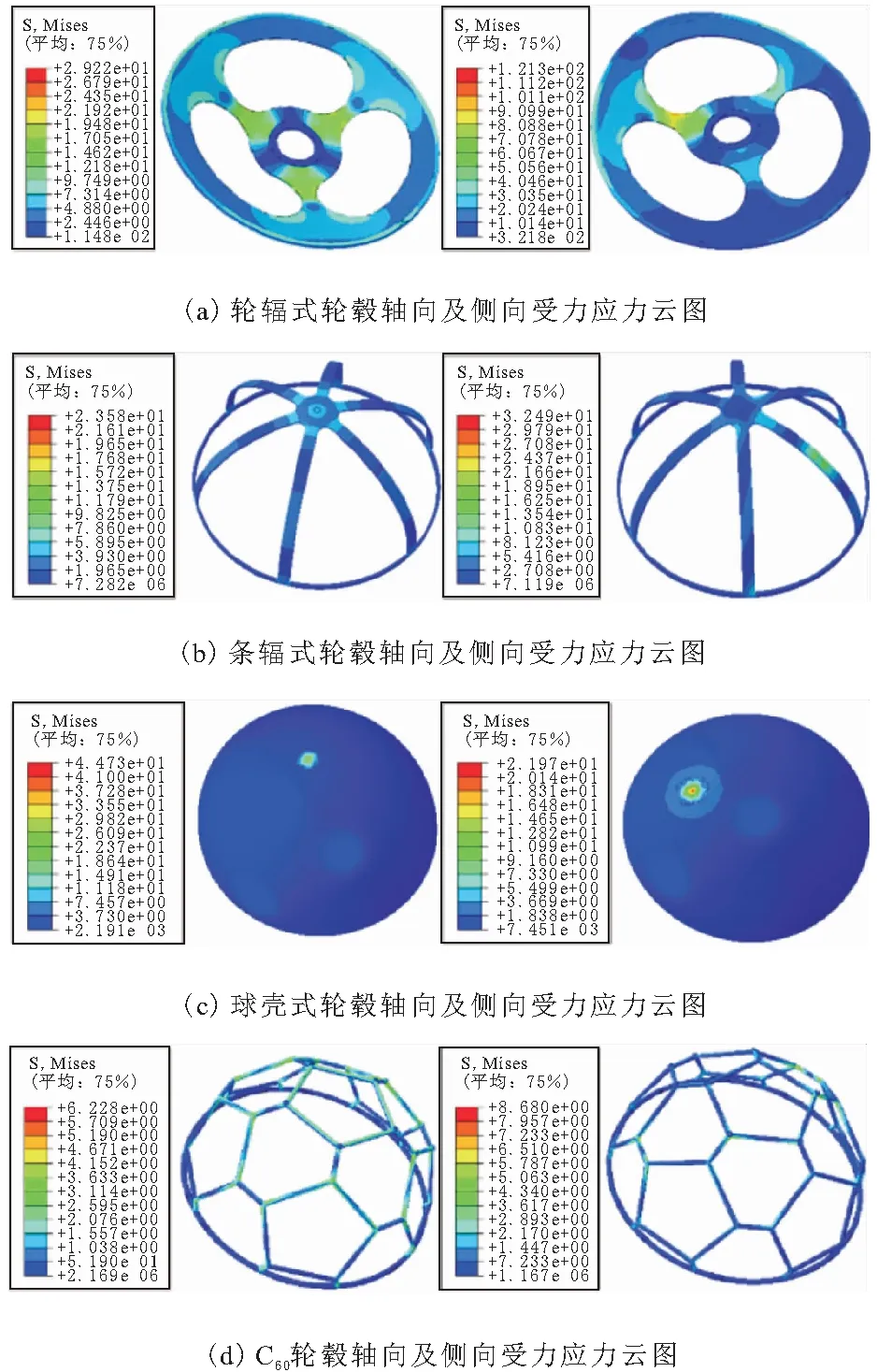
图11 不同轮毂形式轴向承载ABAQUS仿真应力云图
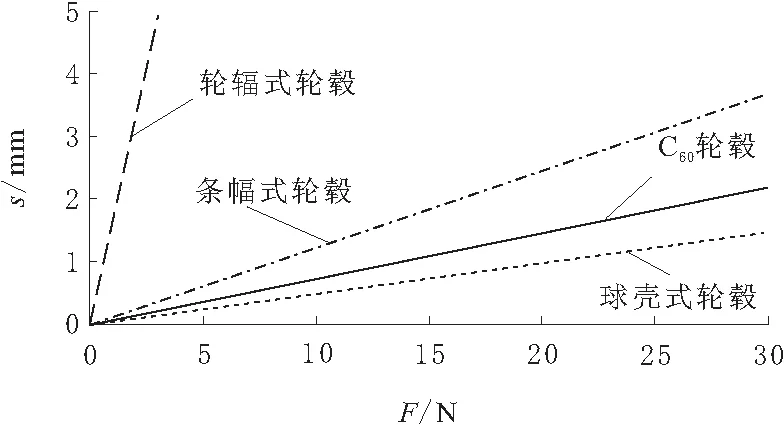
图12 不同轮毂形式轴向承载F-s曲线
4 结束语
本文基于C60模型提出了一种以多边形张拉结构为载荷分布优化单元的双轮式抛投机器人仿富勒烯张拉结构轮毂,通过理论及仿真分析,表明该轮毂具有较好的刚度特性与承载特性,其力学性能优于传统双轮式抛投机器人轮毂。
