基于随机模型的动车组制动模块稳健优化设计

殷 浩，李永华，杜 江

(大连交通大学机车车辆工程学院，辽宁 大连 116028)

0 引言

动车组制动模块受加工制造、老化、疲劳等因素的影响，质量特性均在其目标值附近随机波动，严重影响了制动模块的结构性能。因此，有必要对制动模块的质量特性进行研究，而稳健优化设计是提高质量特性的一种有效方法。

传统的优化设计，往往建立在确定性模型的基础上，没有考虑设计变量在实际运用中的随机性，不能反映产品制造、运营环境等客观因素的随机性对产品质量特性产生的影响[1]。针对这一问题，学者们提出了一种充分考虑设计变量随机性的数学模型来克服传统优化模型的不足。在随机模型提出后，国内外学者开始对基于随机模型的稳健优化问题展开研究。其中，Kanamori[2]通过对损失函数进行改进，提出一种改进的对数损失函数，该函数可以较好地应用于产品的稳健优化设计。Gharib等[3]通过将最小二乘法与损失函数结合，分析了系统的随机误差对计算结果稳健性的影响，提高了系统对随机变量的稳健性。谭晓兰等[4]结合损失函数与可行性准则，研究了随机因素对连杆机构稳健性的影响，获得了更合理的设计变量容差。李丰等[5]结合损失函数，完成了对微机电系统电压的随机稳健优化设计，使得系统运行误差率明显减小。王丽群等[6]结合不合格概率，研究了随机因素对火炮射击密集度的影响，确定出符合指标要求的随机因素的参数区间。以上工作均是针对设计参数或环境因素的随机性而进行的结构稳健优化设计，但这些设计在分析计算过程中，计算复杂，收敛慢。且灵敏度指数作为稳健优化中一个重要的设计指标，很少有学者在对产品进行稳健设计时考虑灵敏度指数对于产品稳健性的影响。灵敏度指数具有考虑因素全面、计算原理简单等特点，可以较好地反映设计变量的变异对产品质量特性的影响。

本文在考虑动车组制动模块设计变量随机性的同时，结合稳健设计的思路，综合考虑灵敏度指数与损失函数对产品稳健性的影响，提出了一种基于随机模型的动车组制动模块稳健优化设计方法。应用Monte Carlo法进行实验设计，从而根据设计变量的概率分布特征建立目标函数与约束条件，构建动车组制动模块的随机稳健优化模型，并结合改进的遗传算法对优化模型进行求解，得到最佳的设计参数，使得动车组制动模块性能更加稳健。

1 基于随机模型的稳健设计

1.1 随机模型

随机模型与其他模型的不同之处在于，随机模型充分考虑了可控因素与不可控因素的随机性，通过调整设计变量并控制其容差来获得最优解[7-8]。为评价产品质量特性的稳健性，共设置了多个产品质量设计准则，其中灵敏度指数与损失函数是2个重要的设计准则[9]。

a.灵敏度指数S。在工程实际中，为了保证产品的优质性，总是希望每一个质量特性的实际值yj与目标值yoj的差异尽量小，为此引入灵敏度指数S来衡量质量特性的优质性，其表达式为

(1)

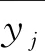
b.损失函数L。损失函数也是检验产品质量特性稳健性的一个重要指标，为保证产品的优质性，不仅希望yj与yoj的差异尽量小，而且希望质量特性的方差尽可能小。为此引入了损失函数L来评价产品质量特性的优质性，其表达式为

(2)

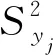
1.2 考虑灵敏度与损失函数的稳健优化模型

为了更好地控制产品的质量，提高产品的优质性。本次研究将综合考虑灵敏度指数与损失函数对产品质量特性的影响，将二者加权整合作为稳健优化的目标，并以设计变量的容差作为约束条件，建立的随机稳健优化模型为

(3)

X为设计变量；F(X)为目标函数；ζ1与ζ2为权重系数；gj(X)≤0为不等式约束。

2 改进的遗传算法

为了提高优化计算效率，通常会结合遗传算法对优化模型进行求解。遗传算法作为一种全局最优搜索算法，具有计算精度高，计算效率快、稳健性好等优点[10-11]，广泛应用于多种领域。

但是，传统的遗传算法只是在某一个种群内对个体进行优化选择，种群单一，且进化过程会出现一些不满足设计要求的个体，导致进化效率较低。因此，对遗传算法做出如下改进：

a.建立多个种群，打破种群单一性。从各种群内随机选择某个个体作为“移民”因子，将其引入其他种群，实现各种群之间的“基因”交流、协同进化，加快进化的效率。再从各种群中选择出优良的个体组成“精英”种群，通过多代进化，选择出整体适应性最优良的个体。

b.改进控制参数。在遗传算法中交叉因子Pc与变异因子Pm都是固定值，虽然可以实现种群的进化寻优，但是极其依赖二者的取值。通过将每个种群的Pc与Pm改为随机值，保证每个种群进化的差异性，使得遗传进化中的新个体更具有随机性，整个遗传算法更具有全局寻优性，其表达式为：

Pc=a+(b-a)×rand(1,Mp)

(4)

Pm=c+(d-c)×rand(1,Mp)

(5)

a和b分别为Pc的上下限；c和d分别为Pm的上下限；Mp为种群数目。

c.增加“惩罚”因子。运用遗传算法进行求解时，过程中会产生一些不满足设计要求的个体，为了避免这些个体对算法的求解效率产生影响，在遗传算法中增添“惩罚”因子，对不满足要求的个体目标函数乘以一个较大的惩罚系数，使其在种群进化中被自动剔除，保证种群内的个体的优良性，减小优化求解过程中的误差，提高求解效率，其表达式为

(6)

c0为惩罚系数；x为种群内的个体；Fobj(x)为个体的目标函数；Ω为设计域。

3 考虑灵敏度与损失函数的稳健优化流程

综合上述分析，考虑灵敏度指数与损失函数的稳健优化设计流程如图1所示。其主要步骤如下：

a.确定设计变量。确定影响产品稳健性的设计变量，并将其分为可控因素与不可控因素，根据各变量的特点确定其分布类型。

b.确定设计准则。在本次稳健优化设计中，选择随机模型中的灵敏度指数与损失函数作为优化准则，进一步研究设计变量的随机性对产品质量特性稳健性的影响。

c.建立随机稳健优化模型。应用Monte Carlo法对设计变量进行模拟抽样，根据抽样结果计算得到设计变量的均值与方差，从而确定灵敏度指数与质量损失函数，并将二者的加权函数作为优化目标，以设计变量的容差作为约束条件，构建随机稳健优化模型。

d.优化求解。对遗传算法进行相应改进，采用改进的遗传算法对稳健优化模型进行求解，得到优化模型的全局稳健最优解。

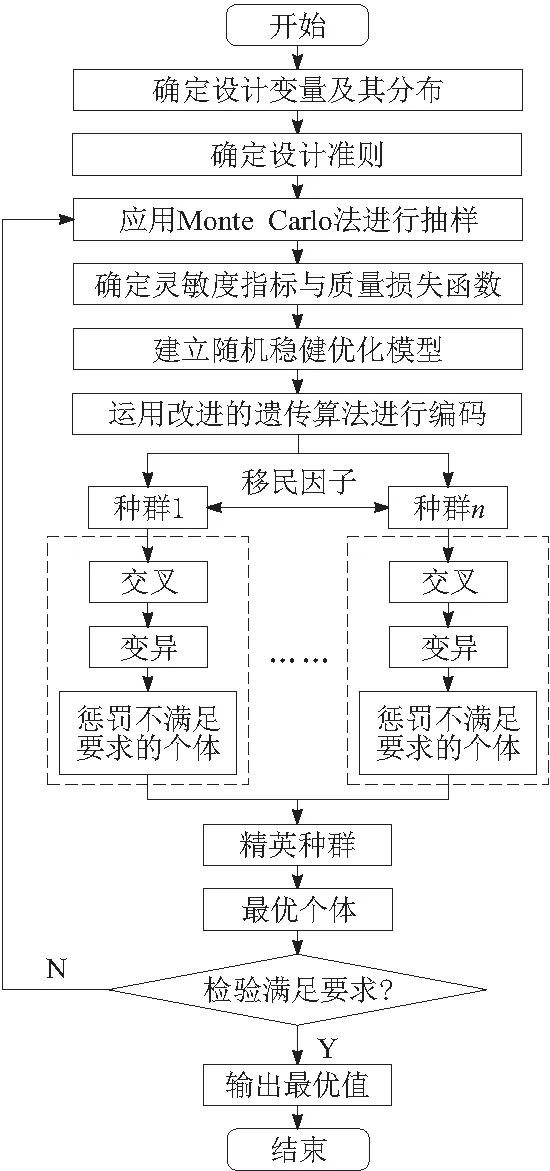
图1 基于随机模型稳健优化流程

4 实例分析

4.1 动车组制动模块模型

动车组制动模块通过螺栓与车体底架相连，其结构主要由吊架与车载电源箱组成，结构如图2所示，整体质量为0.299 t。吊架作为整个结构的承重部件，其材料为低碳钢，车载电源箱为制动模块的电气控制装置提供安装空间，其材料为00Cr17Ni17不锈钢，具体材料参数如表1所示。由于列车在线路运行时，会受到不同载荷冲击，这会对制动模块的结构性能产生相应的影响。考虑制动模块在正常运行过程中受到的载荷情况，选择对其施加的工况为：横向加速度为-1g；纵向加速度为+3g；垂向加速度为+1.5g，其中g=9.81 m/s2。综合考虑该工况下制动模块的结构性能，完成对制动模块的稳健设计。

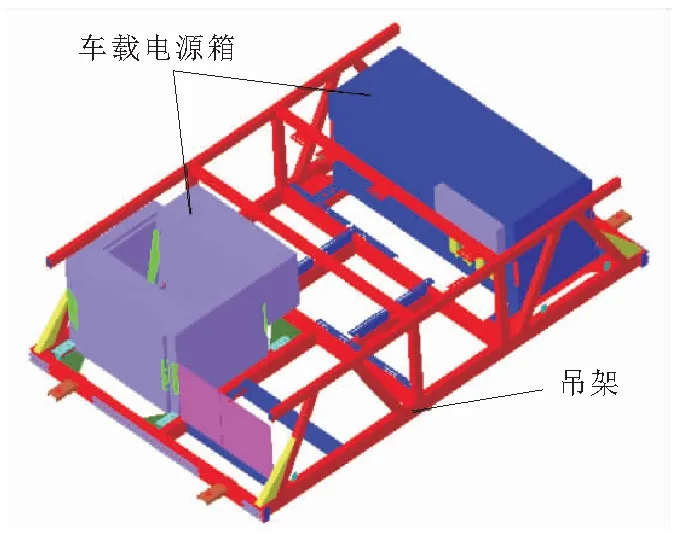
图2 动车组制动模块结构示意

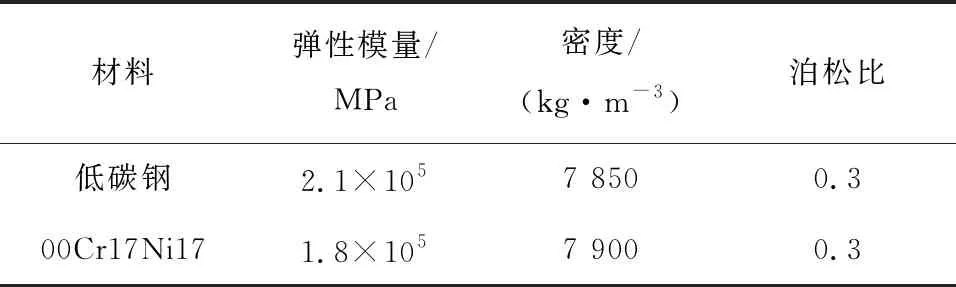
表1 制动模块材料参数

4.2 确定设计变量

动车组制动模块吊架是整个制动模块的主要承重结构，但在实际生产及运用过程中，吊架结构的板材厚度与材料特性并不能达到设计的目标值，而是在目标值附近随机波动。为了保证该结构的稳健性，选择制动模块吊架的板材厚度与材料特性为设计变量。其中，制动模块吊架共有5种厚度的板材(T1～T5)，将各板材厚度作为可控因素，将材料的性能参数(弹性模量E、泊松比μ、密度ρ)作为不可控因素，假设材料密度服从均匀分布，其余设计变量服从正态分布，各参数如表2所示。

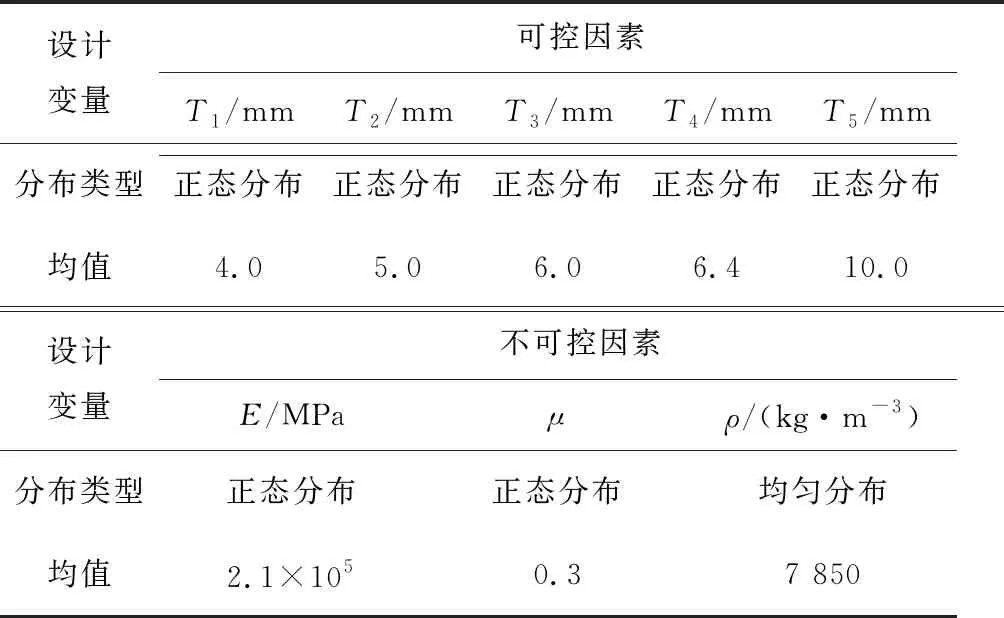
表2 制动模块的主要参数

采用Monte Carlo法对设计变量的可控因素与不可控因素进行500次的简单随机抽样，各设计变量抽样结果的随机分布如图3所示。

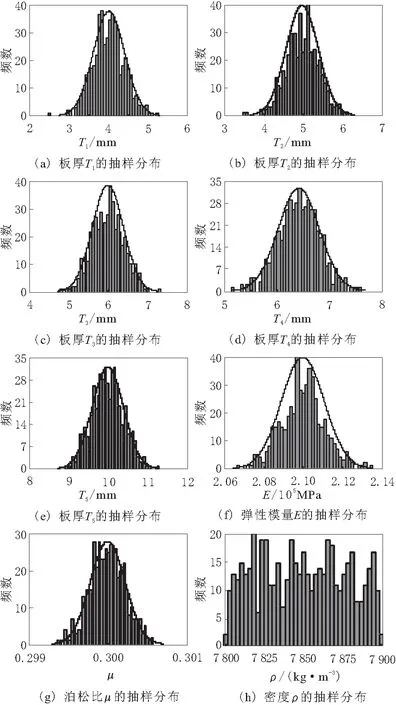
图3 设计变量的Monte Carlo抽样结果

4.3 确定稳健优化设计模型

在考虑随机因素的影响下，为减小制动模块各设计变量的灵敏度指数以及制动模块质量的实际值与目标值的差异，减少质量波动，实现稳健优化设计。综合运用随机模型稳健设计中灵敏度指数与质量损失函数2个设计准则，将其加权整合作为稳健优化目标，进行优化，实现制动模块的稳健设计。

将Monte Carlo抽样所得数据代入式(1)，得到制动模块的灵敏度指数为

S=|4.003-xT1|×|4.967-xT2|×|5.995-xT3|×

|6.4-xT4|×|9.985-xT5|×5×|2.1-xE|×

2 000×|0.3-xμ|×3.333×|7.849-xρ|

(7)

xT1，xT2，xT3，xT4，xT5，xE，xμ，xρ为各设计变量。

将Monte Carlo抽样所得数据代入式(2)得质量的损失函数为：

(8)

(9)

通过权重系数将灵敏度指数和质量损失函数进行整合，作为稳健优化的目标函数，即

F(X)=ζ1×S+ζ2×L→min

(10)

ζ1和ζ2为权重系数。本次研究侧重考虑了灵敏度指数对制动模块的影响情况，因此取ζ1=0.7，ζ2=0.3。

考虑到各设计变量的随机性，在稳健设计时要保证设计变量中可控因素不超过规定的容差范围，其表达式为

(11)

因此，建立以制动模块吊架板材厚度与材料参数为随机设计变量，以可控设计变量的容差为约束条件，灵敏度指数与质量损失函数的加权函数为优化目标的制动模块的稳健优化设计模型为

(12)

X为设计变量；F(X)为目标函数；xTn(n=1,…,5)为设计变量的可控因素；Δx为各设计变量所允许的容差。

4.4 稳健优化设计

运用MATLAB软件对优化模型进行求解，其中，结合改进的遗传算法对稳健优化模型进行求解时，共设置了10个种群，交叉因子Pc∈[0.7，0.9]，变异因子Pm∈[0.01,0.05]，经过多代进化后结果趋于收敛，改进前后的算法优化过程曲线如图4所示。

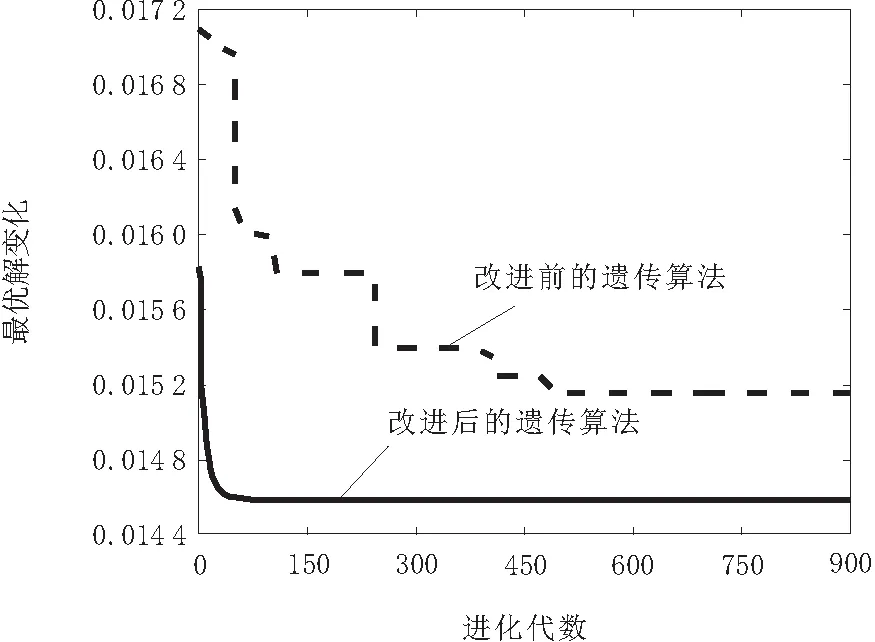
图4 优化求解过程

由图4可知，改进前的遗传算法需要近500代进化才可得到最优解，而改进后的遗传算法仅需100代进化就得到了最优解，求解效率有较大的提高，且求解结果更优。各优化方案的优化结果对比如表3所示。

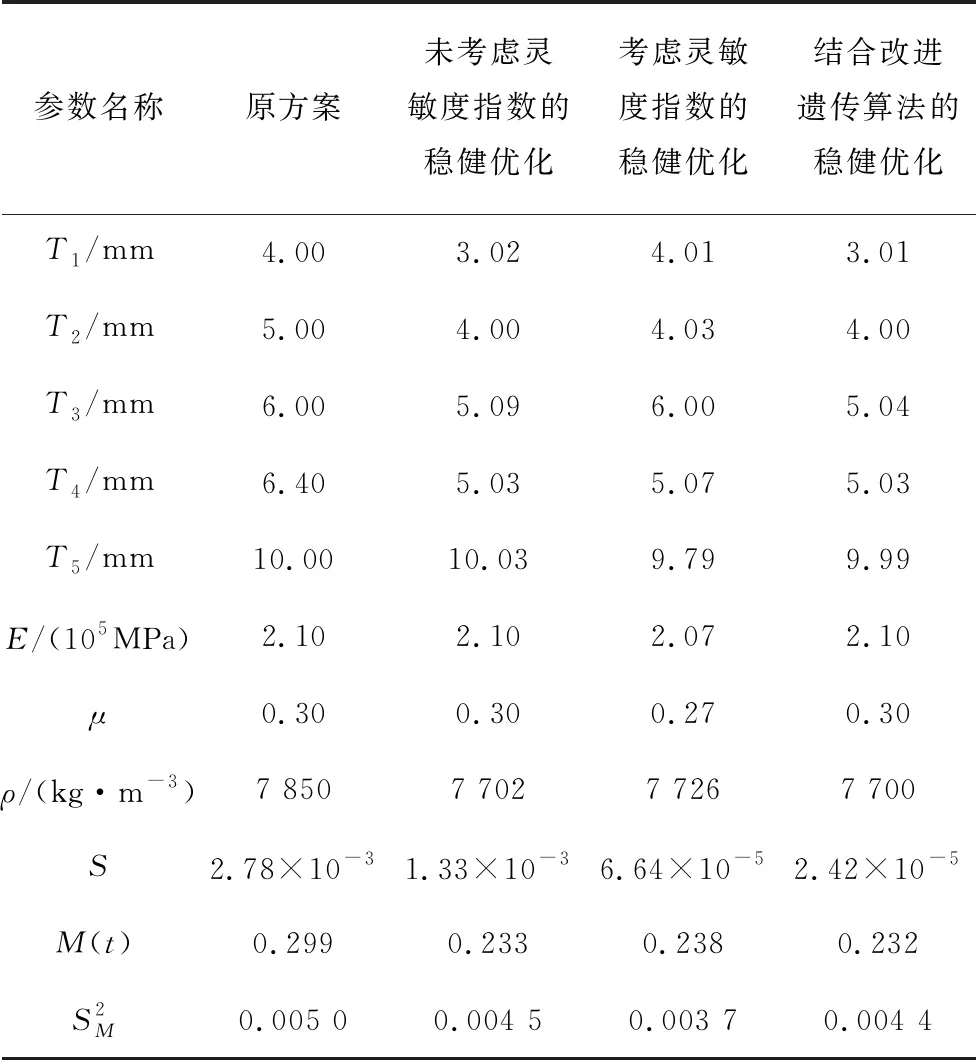
表3 稳健优化设计方案结果对比

由表3可看出，经稳健优化后，制动模块结构质量的方差减小，且结构质量减轻，说明设计变量的随机性对结构质量的影响减小。相较未考虑灵敏度指数的稳健优化方案，在考虑了灵敏度指数之后，制动模块设计变量对结构的灵敏度得到极大改善，结果更加稳健，提高了制动模块的抗干扰能力，进而有效地保证了制动模块各质量性能的稳健性。此外，经过对比可以发现，改进后遗传算法的求解效率有所提升，且求解结果更优。

5 结束语

在考虑了动车组制动模块设计变量随机性的基础上，提出了一种综合考虑灵敏度指数与质量损失函数的稳健优化方法。

通过结合随机模型和改进的遗传算法对动车组制动模块进行稳健优化设计，得到优化模型的全局稳健最优解。使制动模块的结构灵敏度减小，结构质量方差较小，说明设计变量的随机变差对制动模块稳健性的影响减小，提高了制动模块的抗干扰能力。而且改进的遗传算法求解效率明显提高，优化结果更加优良。

对动车组制动模块的稳健优化实例表明，本文的方法具有可行性，可为动车组其他部件的稳健优化设计提供一定的参考，具有一定的实际意义。