船用仓储新型链式传动离合装置的受力分析与优化设计

于文超，吴金波

(华中科技大学船舶与海洋工程学院，湖北 武汉 430074)

0 引言

传动离合装置广泛应用于印刷机、压力机、纺纱机、焊机和切割机等机械设备[1]。离合装置按其传动原理不同，可分为摩擦式和嵌合式。摩擦式离合装置主、从动件通过接合面间摩擦力传递动力；嵌合式离合装置主、从动件通过相互配套的嵌合结构传递动力。常见摩擦式离合装置有片式和圆锥式。摩擦接触片间相对滑动导致其易发热、磨损快、寿命短。圆锥式结构尺寸大，轴向移动困难[2-3]。常见嵌合式离合装置有牙嵌式、齿式和转键式。牙嵌式对接合位置精度要求高，若有偏差，其牙形结构极易损坏。齿式嵌合结构制造成本高，且接合过程中易出现打齿现象。转键式最多有2个转键，接合难度大，且单键式只可单向转动[4-5]。

为解决上述问题，本文提出了一种新型链式传动离合装置。该装置由主动链条传递动力给从动链轮。主动链条采用三排链形式，其对接部分采用长滚子结构，即使链条与链轮对接位置存在偏差时，仍可正确啮合，降低对接难度。链节间由销轴连接可相对转动，因此链条有一定的顺应能力，可减弱接合部分刚性碰撞导致的磨损，提高装置的使用寿命。

1 船用仓储系统及新型链式传动离合装置

自动化仓储系统以人力成本低、仓库密集度高和运输效率高等优点，广泛应用于汽车、烟草、医药、白酒和食品等行业[6-7]。陆用自动仓储系统一般采用高层多巷道单元储位式立体仓库以提高货物存储量。由于船用自动仓储系统仓库形状受到船体结构尺寸制约，为提高仓库密集度，通常采用低层单巷道多元储位式(即：单个货位纵深方向可存储多个托盘)立体仓库。本文涉及的船用自动仓储系统如图1所示，船体右舷到左舷为X轴方向，艉部到艏部为Z轴方向。移载设备可沿X轴和Y轴方向移动与仓库内任意货位对接，并通过链式传动离合装置将动力传递给货架上的输送链，完成货物沿Z方向的转运。而传动离合装置位于移载设备上，货架输送链无需单独设置动力源，因此提高了设备的空间利用率。船用货架如图2所示。

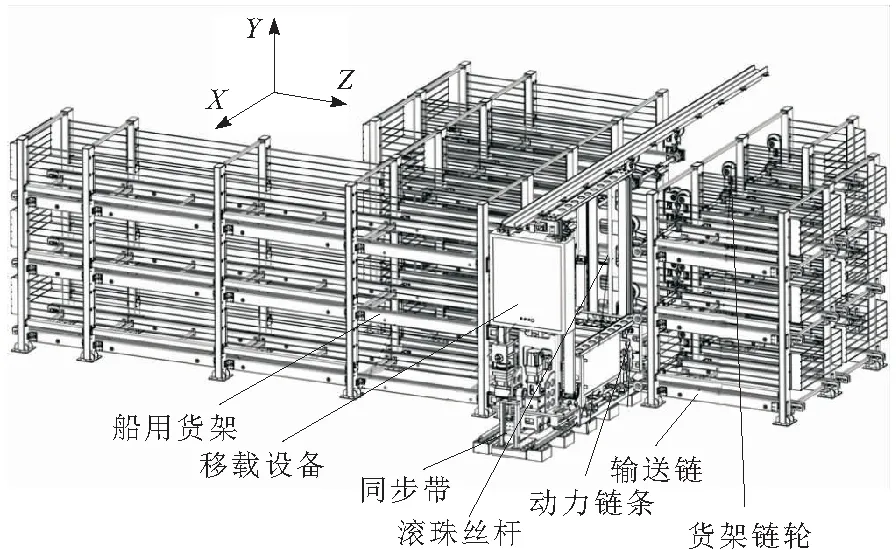
图1 船用自动仓储系统示意

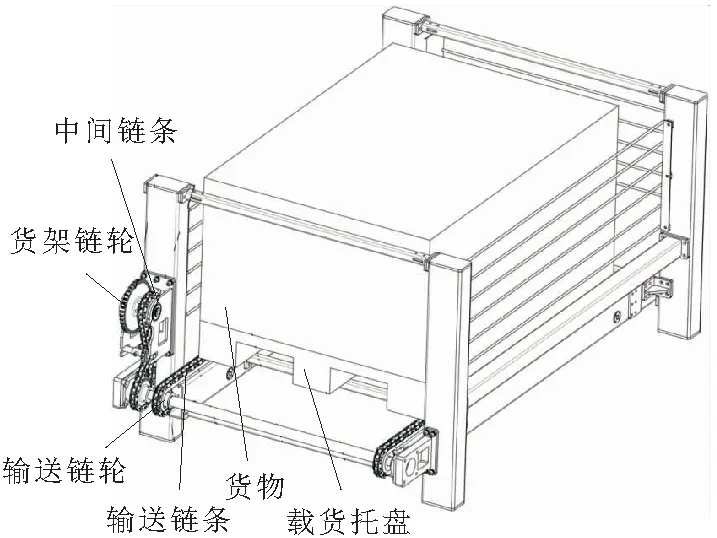
图2 船用货架示意

本文研究的新型链式传动离合装置如图3所示。传动离合装置可在电动推杆的作用下沿导轨左右移动与巷道两侧货位对接。动力链条为三排滚子链结构，其两侧滚子链与电机驱动轮啮合，中间链采用长滚子结构，即使对接位置稍有偏差，仍可顺利与货架链轮啮合。对接过程中，链轮齿和链条滚子不断啮合，链条内部张力增大，推动张紧轮沿滑槽上移。装置移动到指定位置后，挡块触发限位开关，推杆停止运动，链条与链轮接合完毕。电机驱动轮通过动力链条驱动货架链轮，并经由中间链条传递动力给输送链，实现货物的存入或取出。装置内部结构以及链条-链轮接合前后对比情况如图4所示。

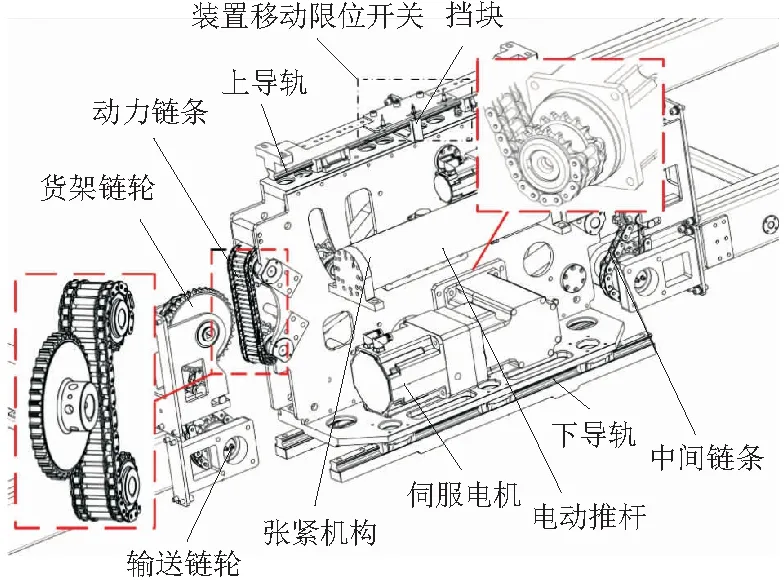
图3 新型链式传动离合装置

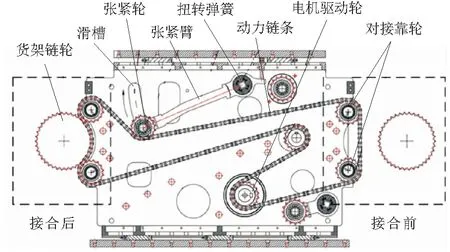
图4 装置内部以及链条-链轮接合前后对比

然而，动力链条可能出现滚子跳齿现象导致其无法传递动力给输送链。跳齿是一种常见的链传动失效现象。跳齿瞬间，参与啮合的链条滚子所受载荷激增，严重时可拉断链节。因此新型链式传动离合装置转运货物需避免链条滚子跳齿现象以保证转运过程稳定可靠。

2 链传动原理及跳齿

链传动出现滚子跳齿现象与其传动原理有关，链传动简化原理如图5所示。主动轮逆时针旋转，链条a边链节张力逐渐增大。当a、b边张力差产生的驱动扭矩大于从动轮的负载扭矩时，从动轮逆时针旋转。由于链条a边链节张力大于链条b边链节张力，称a边为紧边，b边为松边。链条紧边对链轮的作用力Tt称为紧边张力，链条松边对链轮的作用力Ts称为松边张力[8]。

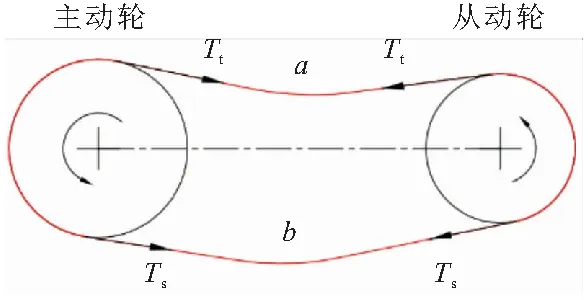
图5 链传动原理

部分链条滚子与链轮齿啮合情况简化示意如图6所示。

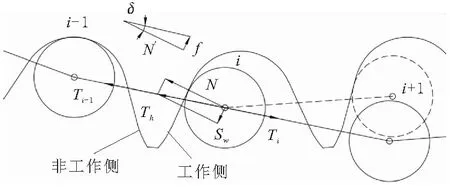
图6 链条滚子与链轮齿啮合

第i个滚子两侧链节张力Ti与Ti-1的合力为Th。当Th沿轮齿工作侧方向的分力Sw大于轮齿能提供的最大静摩擦力f时，滚子沿链轮齿移动。若滚子与轮齿滑动摩擦系数较小，则滚子沿齿面滑动；若滚子与链节衬套滚动摩擦系数较小，则滚子沿齿面滚动。当其移动超出链轮工作侧齿面，滚子产生跳齿现象。

3 链传动受力分析

链条提供给从动轮的有效圆周力为从动轮两侧链条紧边和松边张力之差。由于滚子跳齿现象主要发生在从动轮的松边，因此为保证链传动过程稳定可靠，链条松边应有一定的预紧力[9-11]。扭转弹簧通过张紧轮给链条施加压力，使链条保持张紧状态。张紧轮两侧链条张力的合力与该压力大小相等，方向相反。初始状态下，张紧轮两侧链条夹角一定，故张紧轮对链条压力越大，链条内部预紧力越大，其初始松边张力值越大。

为研究传动过程中链条紧边张力与松边张力的关系，作出以下假设：链条节距与链轮弦节距相等，无加工和安装误差；链传动处于低速级，忽略滚子所受离心力；链条滚子质量较小，忽略其重力影响。考虑摩擦力和不计摩擦力时滚子受力情况对比如图7所示。

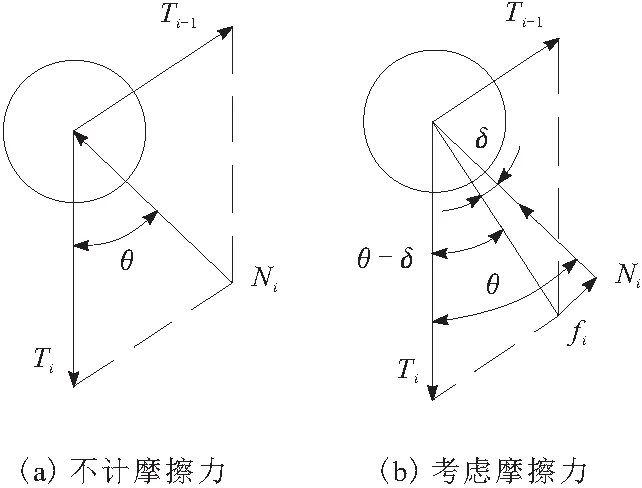
图7 滚子受力对比

考虑摩擦力时，滚子所受摩擦力和接触力的合力与其相邻两链节间张力产生了新的受力平衡。因此将摩擦力的影响转化为滚子压力角的变化。此时，滚子所受相邻链节间张力为：

(1)

(2)

Ti为第i个链节的张力；Ti-1为第i-1个链节的张力；θ为滚子与链轮齿的平均接触角；δ为滚子与链轮齿的平均摩擦角；α为链轮的节距角；Zh为货架链轮齿数。由参与啮合的第一个滚子1递推到参与啮合的最后一个滚子n，可得从动链轮两端紧边张力Tt和松边张力Ts的关系为：

(3)

(4)

n为链条与链轮啮合的滚子数;β为链条包络链轮的围角。

输送链转运货物时，货架链轮两侧链条松紧边分布情况与其转向有关。当链条松边靠近电机驱动轮侧时，链条无法形变故不易产生跳齿现象；而链条松边靠近张紧轮侧时，其松边张力与张紧轮对链条的压力有关。若压力过小，链条松边张力值较小，紧边张力与式(3)右侧的乘积远大于松边张力值。此时，滚子所受合力沿轮齿工作侧方向分量大于最大静摩擦力，产生滚子跳齿现象。因此传动过程中，为确保链条滚子不发生跳齿现象，需满足

(5)

由图7可知，摩擦力的影响使滚子所受两侧链节张力比增大，在松边张力一定的情况下，更不易发生跳齿。因摩擦角在实际系统中较难测定，根据系统设计的保守性，忽略摩擦力的影响，从而估计出传动离合装置能够传递的最大圆周力为

(6)

由式(2)～式(6)可知，松边张力、包络角、链轮齿数和滚子与链轮的接触角共同决定了装置可传递的最大圆周力。其中，包络角和链轮齿数共同决定了参与啮合的链条滚子数n。相同链轮齿数下，包络角越大，啮合滚子数越多，越不易产生跳齿；相同包络角下，链轮齿数越多，啮合滚子数越多，越不易产生跳齿。

4 优化设计

由图2可知，动力链与输送链的链速比等于货架链轮与输送链轮的半径比。因此输送链运输载荷一定时，货架链轮直径越大所需动力链提供的圆周力越小，动力链滚子越不易产生跳齿。但船用仓库空间宝贵，货架链轮直径过大，降低了空间利用率。结合式(6)可知，若选择较小的链轮直径，链条所需松边张力过大难以实现。因此为保证系统转运过程安全可靠并降低张紧机构的实现难度，以最小货架链轮直径和最小松边张力为设计目标，选择动力链条链速和链条节距值作为约束条件并采用遗传算法求解。

4.1 目标函数

根据线性权重系数法[12]，把多目标优化问题转化为单目标优化问题并无量纲化为

(7)

f1(x)和f2(x)分别为货架链轮直径和松边张力值的目标函数；α1和α2分别为f1(x)以及f2(x)的权重系数；f10和f20分别为货架链轮直径和松边张力的预估初值。

(8)

dh为货架链轮直径；Zh为货架链轮齿数；p为链条节距。

结合式(6)和式(8)可知，当链条传递最大圆周力与货架链轮所需圆周力相等时，其松边张力值为

(9)

Fm为转运货物时输送链条所需的总输送力；dc为输送链轮的直径；η2和η3分别为中间链和输送链的机械效率。

由上文可知，链条不发生跳齿现象其松边张力值始终大于式(9)右侧表达式，故最小松边张力值应等于式(9)右侧表达式的最大值。因此松边张力值的目标函数为

f2(x)=-Ts

(10)

由图1可知，船体横摇时，输送链转运货物需克服其与导轨侧板之间的额外摩擦力Fh；船体纵摇时，输送链转运货物需克服爬坡运动重力沿输送链分量带来的额外阻力Fz；货物加减速时，输送链需克服惯性力来转运货物。

Fm=Fss+Fh+Fz+ma

(11)

Fss=Csmg

(12)

Fh=Ccmgsinξ

(13)

Fz=mgsinσ

(14)

Fss为船体无倾角时，转运货物所需输送力；m为货物、托盘以及输送链条的质量总和；a为货物加速度；Cs为输送链条与直线导轨的滑动摩擦系数；Cc为输送链条与导轨侧板的摩擦系数；ξ为船体的横倾角；σ为船体的纵倾角；g为重力加速度。

4.2 参数选择

选择货架链轮齿数Zh、链条节距p、链轮包络角β作为设计变量，其取值范围如表1所示。

x=[x1,x2,x3]T=[Zh,p,β]T

(15)

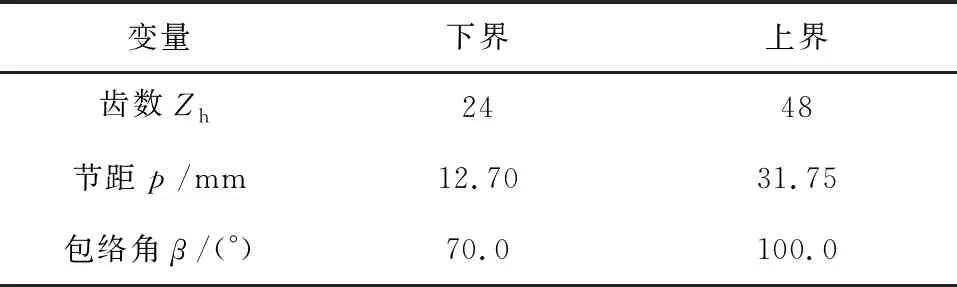
表1 设计变量取值范围

4.3 约束条件

传动离合装置的多级链传动为减速传动，为减弱多边形效应影响，将动力链条链速设为低速级，其表达式为

(16)

vs为输送链条运输货物的速度；v0为低速级链传动的链速上限。

为保证系统可靠运行，链传动其传递的计算功率[P]必须小于其许用功率Ps：

h2(x)=KAP-kzkikaknP0≤0

(17)

[P]=KAP

(18)

Ps=kzkikaknP0

(19)

(20)

P0为单列链可传递功率；KA为链条工况系数；kz为小链轮齿数系数；ki为传动比系数；ka为中心距系数；kn为多排链系数；η1为动力链的机械效率。链传动设计中，使用图表较多，为方便计算，对其系数公式化[13]为：

(21)

(22)

ka=0.713 32+0.008 5×(al/p)-

0.000 1×(al/p)2/3

(23)

(24)

(25)

(26)

Zm为电机驱动轮齿数；al为电机驱动轮与货架链轮中心距；nl为链条排数；nm为电机驱动轮转速。

采用外点惩罚函数法，将有约束的优化问题转化为无约束的优化问题[14]，此时新的目标函数变为：

(27)

(28)

r为惩罚因子；k为当前迭代次数。其余系统参数如表2所示，其中Cs和Cc通过实验测得。

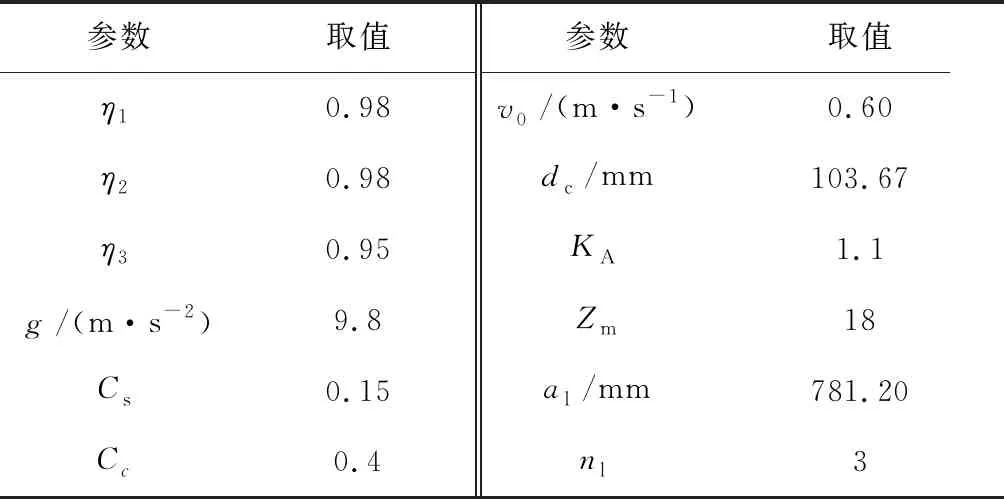
表2 系统参数

4.4 遗传算法

链轮齿数为正整数，故选择适用于离散问题的遗传算法进行求解[15]。遗传算法流程如图8所示。选择群体规模N=60，交叉概率pc=0.6，变异概率pm=0.01，迭代次数Dn=2 000，根据设计变量的上、下限和其离散精度进行编码得到含有不同基因的染色体。采用轮盘赌的方式计算种群个体适应度占种群总适应度的百分比，从而更新种群。

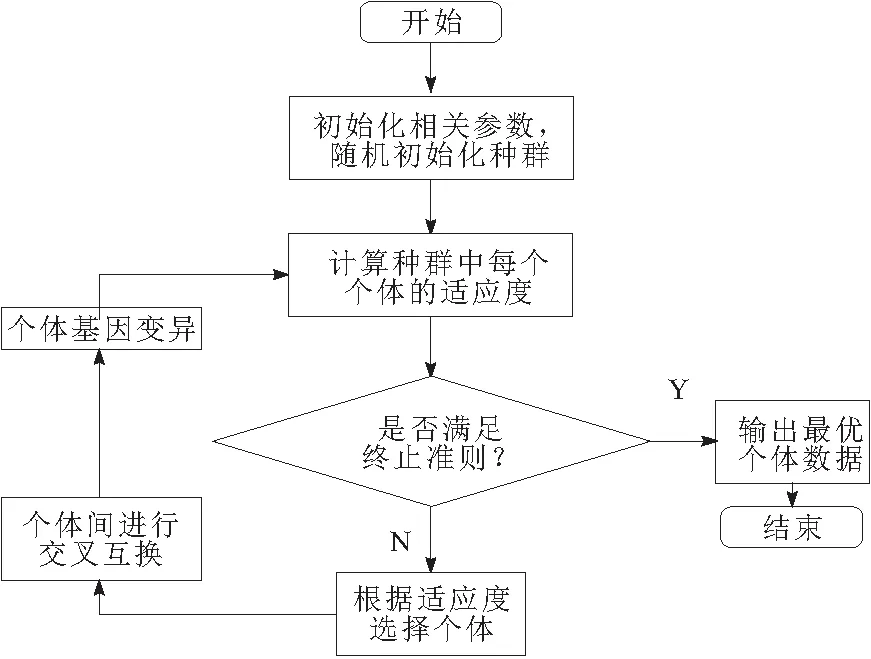
图8 遗传算法流程

5 验证与结论

本文涉及的船用仓储系统单个货位纵深方向最多布置7个托盘，单个托盘和其承载货物质量和最大为1 000 kg。因此计算质量为7个载货托盘与输送链质量总和。输入输送链转运速度、船体横纵摇最大倾角，货物加速度和滚子接触角并优化求解，输入参数如表3所示，优化结果为：货架链轮齿数Zh为38；链条节距p为18.92 mm；链轮包铬角β为95.2°。

表3 输入参数

查机械手册，选取与优化结果最相近的链条型号12 A，其节距值为19.05 mm。经计算可知，该包络角度下，链轮参与啮合传动齿数为10.05个。四舍五入得其啮合传动齿数为10个，此时新的包络角度β=94.7°。最终确定各个设计变量的值：货架链轮齿数Zh=38；链条节距p=19.05 mm；链轮包络角β=94.7°。此时，链轮直径dh=230.7 mm、松边张力Ts=0.531 kN。

将优化结果代入式(6)，可得出动力链条不发生跳齿所允许的最大载荷，并通过仿真实例模拟输送链的转运过程。输送链运输货物过程中横纵摇附加载荷、加减速载荷以及运输所需总载荷与时间关系曲线如图9所示。

由图9可知，转运货物所需运输力始终小于不发生跳齿所允许的最大载荷，故系统转运货物过程中不会出现滚子跳齿。由于篇幅所限，本文只得出了链条所需最小松边张力值和货架链轮最小直径，而未介绍系统建模过程和张紧机构的设计，直接给出数值计算结果以证明优化设计的有效性。

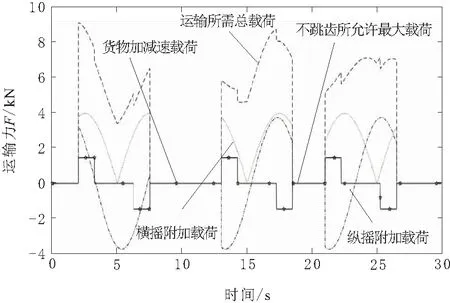
图9 载荷与时间关系曲线

6 结束语

研究了一种新型链式传动离合装置，根据链传动原理分析了链条滚子跳齿的力学因素。为提高系统的空间利用率，综合考虑了链轮直径与松边张力的关系，利用优化设计方法得出了装置的关键设计参数。并通过数值计算验证了设计的有效性。