GPT2w 对流层延迟模型在中国区域的精度分析
2020-10-22张永林
张永林,李 磊
(中国电建集团 昆明勘测设计研究院有限公司,昆明 650033)
0 引言
全球卫星导航系统(global navigation satellite system, GNSS)信号从太空端到达地面时,会受到电离层误差和对流层误差的影响。由于电离层误差和GNSS 的信号频率相关,通常可以通过不同频率的信号组合削弱其影响。而对流层对于GNSS信号而言是1 种中性介质,其造成的误差与信号频率无关,通常只能将其作为未知参数估计或者通过外部模型进行削弱,许多学者对对流层误差模型进行了深入研究。如果能获得观测时刻的气压和温度等气象元素,可以通过萨斯塔莫伊宁(Saastamoinen)模型或者霍普菲尔德(Hopfield)模型等进行改正[1-2]。文献[3]系统分析了不同对流层模型在中国区域的精度情况,统计结果表明,由数值天气模型输出的再分析资料计算的对流层延迟精度最高,但考虑到数据实时性以及模型的复杂程度,Saastamoinen 模型最符合要求。一般在实际的观测中很少有实测的气压数据,因此许多学者利用再分析资料建立了覆盖全球的对流层延迟模型,这些模型仅需要提供观测时刻的大致坐标以及时间就能获得对应的对流层延迟结果,比较典型的有:文献[4]利用欧洲中期天气预报中心(European Centre for Medium-Range Weather Forecasts, ECMWF)提供的再分析资料ERA-Interim 建立的经验对流层延迟模型GPT2w;文献[5-6]利用ERA-Interim建立的对流层延迟模型ITG,其全球精度大致在50 mm 以内。考虑到全球模型往往在局部区域的精度不是最优,因此有许多区域使用本地的对流层延迟模型,比较典型的有:美国在其广域星基增强系统(wide area augmentation system, WAAS)中使用的新不伦瑞克大学(University of New Brunswick, UNB3)模型;欧盟在其星基增强系统中使用的欧洲静地轨道导航重叠服务(European geostationary navigation overlay service, EGNOS)模型等,在不需要实测气象元素的前提下都可以达到厘米级的改正精度[3,7]。此外,许多学者还尝试利用区域连续运行参考站网络建立对流层延迟模型,例如文献[8]利用主成分分析的方法建立的对流层延迟模型,其精度可以达到20 mm,明显高于Saastamoine 等模型。考虑到人工神经网络对非线性特征具有非常好的拟合效果,因此有学者也尝试利用神经网络建立区域对流层模型。文献[9]利用改进的反向传播(back propagation, BP)神经网络建立的区域模型,其精度可以达到10 mm 以内;文献[10-11]中利用神经网络也得到类似的结果。
中国区域地形及气候条件变化多样,例如海拔从东部平原地区的几米向西过渡到平均高度超过3 000 m 的青藏高原,年降水量从东南沿海超过1 000 mm 逐渐向西北递减至不足50 mm;虽然GPT2w 模型计算的对流层延迟在全球的精度可以达到比较高的精度,但是在中国区域却没有1 个很好的评估结果。本文利用中国大陆构造环境监测网络(陆态网)提供的26 个GNSS 测站在2017 年全年的对流层延迟产品对该模型进行了评估。
1 GPT2w 模型简介
GPT2w 模型是GPT2 模型的延伸,可以提供地面上任意位置的气压、温度、水汽分压以及加权平均温度等参数。这些参数利用1 个包含年平均值、年变化振幅以及半年变化振幅的公式计算,公式的系数利用再分析资料ERA-Interim 的月平均气压层数据拟合而出[4,12]。当利用该模型获得测站所在位置的气象参数时,首先利用Saastamoine 模型计算出该点的天顶干延迟(zenith hydrostatic delay, ZHD),即
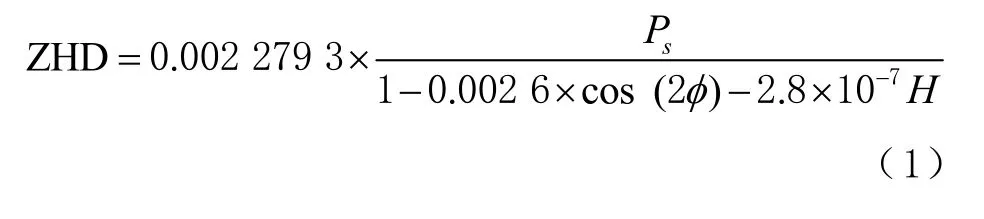
式中:Ps为地面的气压观测值,单位为hPa;φ 为GNSS 测站的纬度,单位为rad;H 为GNSS 测站的高程,单位为km。
然后利用阿斯克涅(Askne)模型计算出该点的天顶湿延迟(zenith wet delay, ZWD)即:
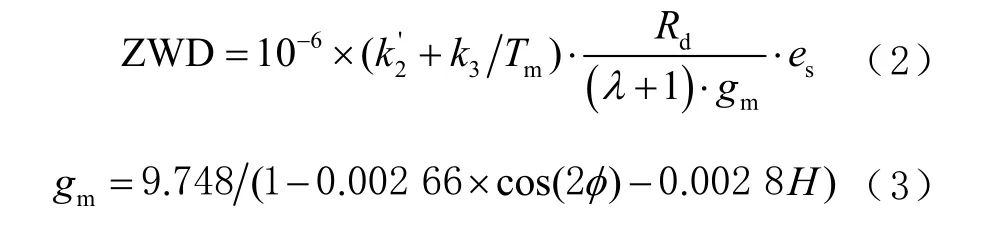
式中:Tm为加权平均温度,单位为℃;k2’=16.52 K/ hPa;k3=(3.776±0.004)×105K2/hPa;Rd=28.964 4 g/ mol,为干空气分量常数;λ 表示水汽递减因子;gm为测站位置的重力加速度,单位为m/s2;es为水汽分压,单位为hPa[13]。
2 者之和即为天顶对流层总延迟(zenith tropospheric delay, ZTD)[4],即
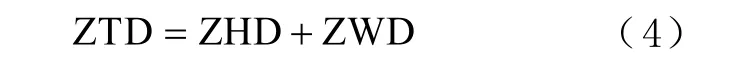
2 实验与结果分析
本文采用来自于陆态网的对流层延迟产品,该产品利用GAMIT/GLOBK 软件进行解算,对流层投影函数为全球投影函数(global mapping function,GMF),卫星截止高度角为10°,每隔1 h 估计 1 次天顶对流层延迟[14]。本文从陆态网中选择分布比较均匀的26 个测站在2017 年全年的对流层延迟数据用于评价GPT2w 对流层延迟模型的精度,其测站位置如图1 所示。
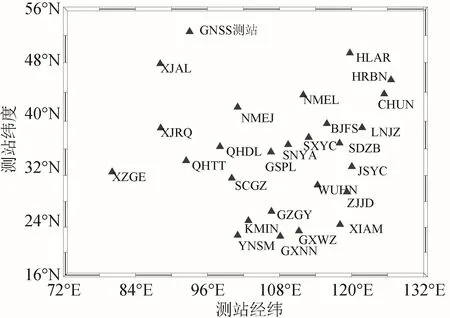
图1 选择的GNSS 站点分布
分别从图1 中选择WUHN、BJFS、NMEJ、XZGE 4 个测站分析GNSS 和GPT2w 计算的天顶对流层延迟全年变化。这4 个测站分别位于中国的南方地区、北方地区、西北地区和青藏高原,分别代表着中国不同的气候类型和地形特征。图2 展现了4 个测站GPT2w 模型和GNSS 计算的对流层延迟变化趋势,2 者具有比较好的一致性。从图2中可以非常明显地看到,对流层延迟随着季节的变化呈现出逐渐升高然后又缓慢降低的趋势,这与我国的季风气候存在明显的相关关系。夏季时太阳直射点北移,东亚地区盛行的东南风携带大量水汽从海洋进入中国大陆,造成对流层湿延迟部分增大,故在图2 中的5 月—10 月出现对流层延迟峰值。此外,从图2 中可以看到XZGE 站的对流层延迟 明显小于其余3 个测站,这与该站海拔较高有关。
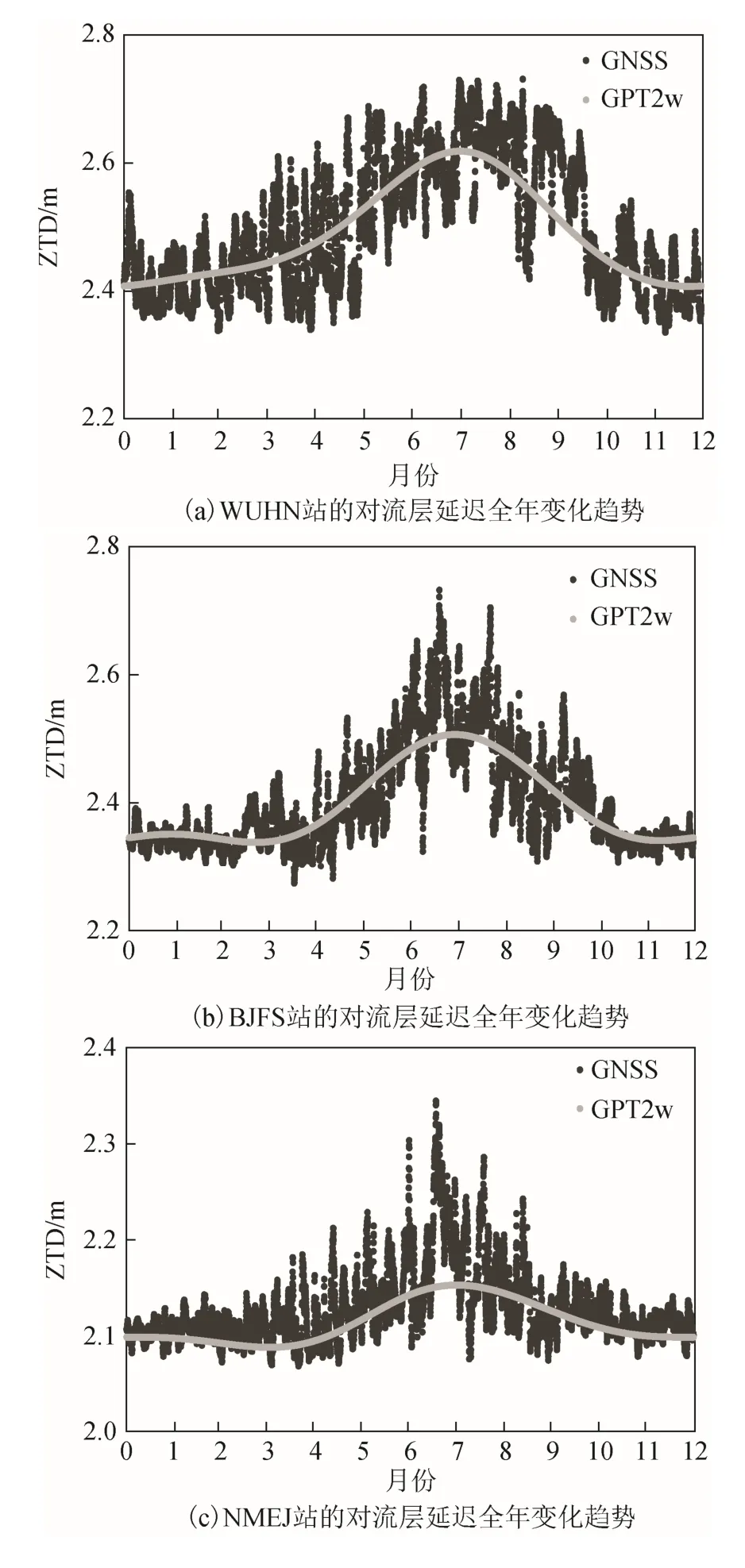
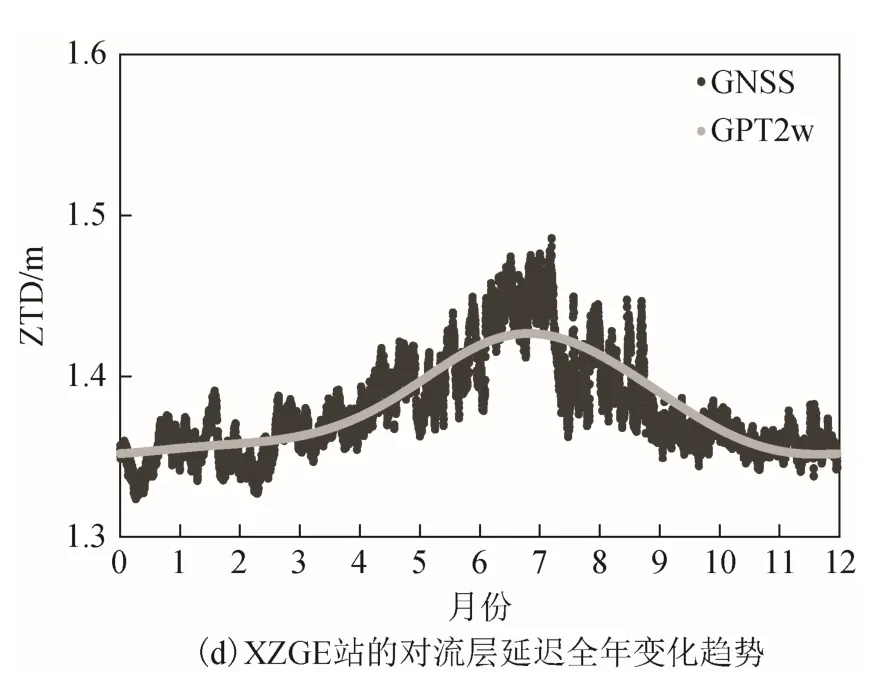
图2 不同测站GNSS 和GPT2w 模型计算的对流层延迟全年变化趋势
图3 显示了GPT2w 模型计算的对流层延迟相对于GNSS 对流层延迟的偏差分布结果。从图3 可以看到4 个测站的偏差基本都在零值上下波动,说明GPT2w 模型没有明显的系统偏差存在。此外,可以发现WUHN 和BJFS 站的偏差变化幅度明显大于其余2 站,因为2 个测站更靠近东部沿海,大气中更为剧烈的水汽变化造成GPT2w 模型精度偏低;而位于青藏高原的XZGE 站,因为当地海拔高,气候寒冷干燥的原因,使得GPT2w 模型的精度明显高于其他3 站。
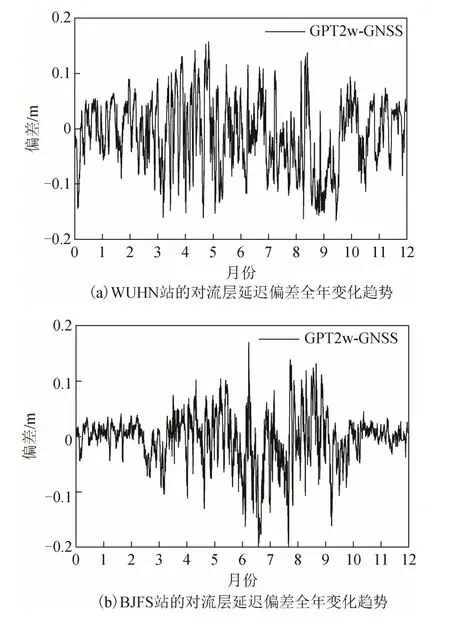
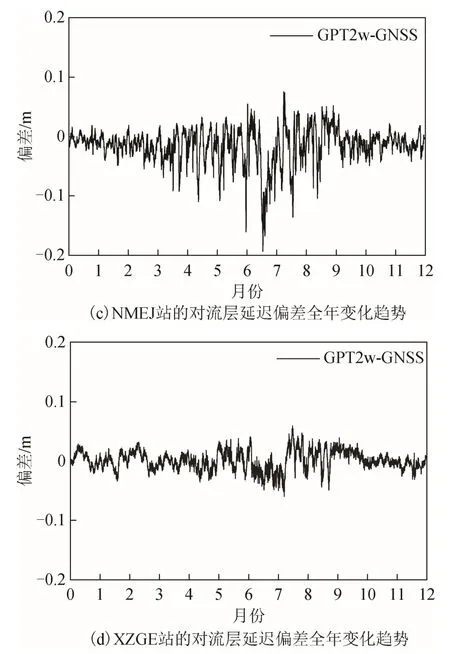
图3 不同测站GPT2w 计算的对流层延迟相对于GNSS 的偏差全年变化趋势
本文选择使用平均偏差(Bias)和均方根误差(root mean square error, RMS)进行GPT2w 模型的精度统计,其计算公式为:
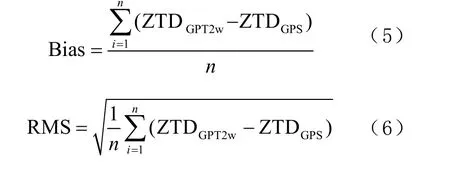
图4 为按照高程由低到高依次排列的所有测站全年的平均偏差和RMS 值的统计结果。从图4(a)中可以看到所有测站的平均偏差都在3 cm 以内,并且偏差随测站高程增加没有明显的函数关系;此外,从图4(a)中可以看到,大部分测站的平均偏差都是负值,与文献[4]中的统计结果类似。从图4(b)可以看到,所有测站的RMS值都在8 cm 以下,而且RMS 值随着高程的增加呈现出逐渐变小的特点。
图5 展示了GPT2w 模型计算的对流层延迟误差在中国区域的分布情况。从图5(a)可知,除了东北地区的4 个测站呈现出比较大的正偏差外,其余地区的平均偏差都趋向为负,特别是南方地区的几个测站。图5(b)显示了RMS 值的分布情 况,误差分布呈现出从东南沿海向西北内陆逐渐递减的规律,这与我国的气候类型从东南沿海炎热潮湿的季风气候向西北内陆干旱少雨的大陆性气候过渡有很好的一致性。

图4 按照高程由低到高依次排列的所有测站GPT2w模型平均偏差和RMS 值统计结果
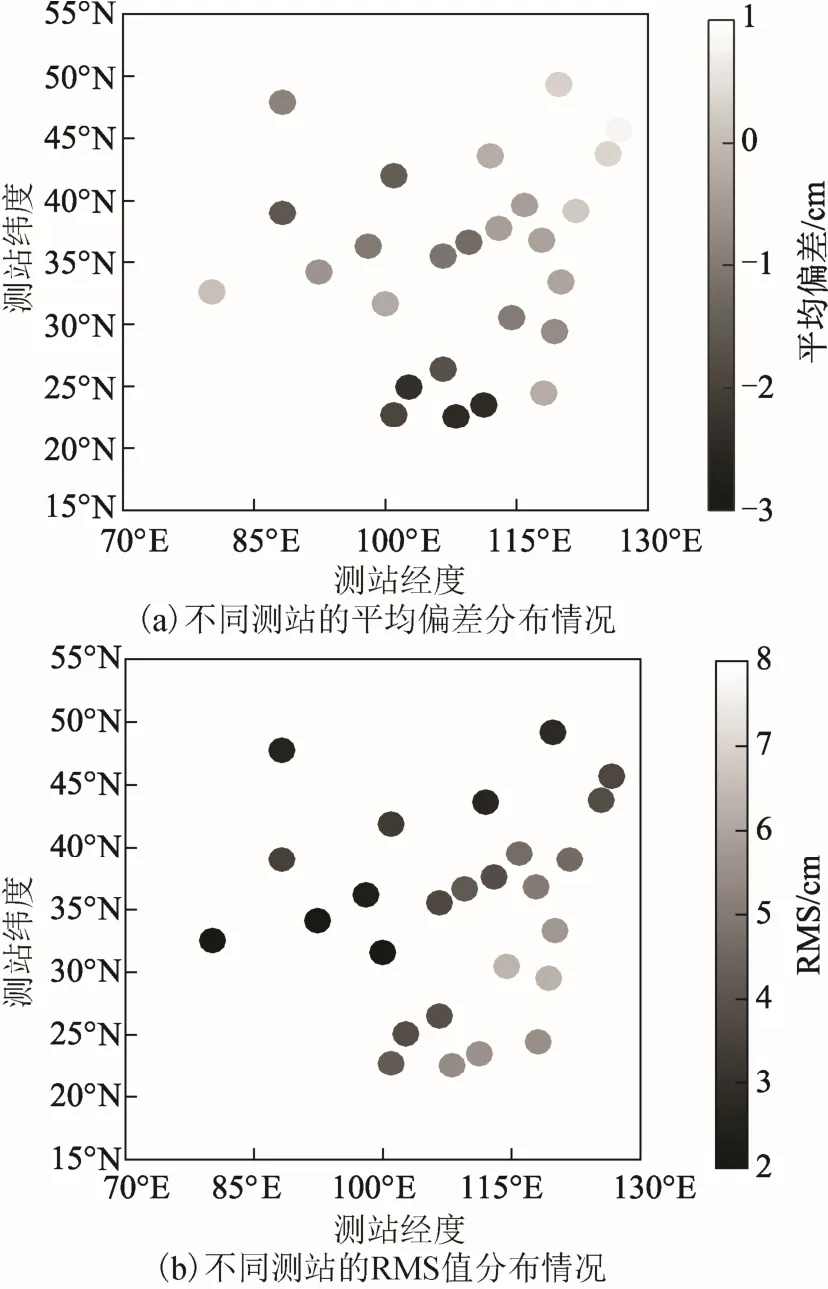
图5 GPT2w 模型计算的对流层延迟平均偏差和RMS值的分布情况
3 结束语
本文利用大陆构造环境监测网络提供的26 个GNSS 测站在2017 年全年的对流层延迟产品详细评估了GPT2w 模型计算的对流层延迟在中国的精度情况,得出了以下结论:
1)GPT2w 模型在中国区域的平均偏差在3 cm 以内,偏差随着测站高程的增加没有明显的函数关系,此外,除了东北地区的偏差趋向于正值外,其余地区的偏差趋向于负值。
2)GPT2w 模型在中国区域的RMS 值在8 cm以内,并且RMS 值随着测站高程的增加有逐渐减小的规律,此外,RMS 值也表现出从东南沿海逐渐向西北内陆递减的规律。
