国产SOHM-4 型氢钟长期性能分析
2020-10-22刘峰宇王宇谱李锡瑞
刘峰宇,王宇谱,2,李锡瑞
(1. 北京卫星导航中心,北京 100094;2. 武汉大学 卫星导航定位技术研究中心,武汉 430079; 3. 中国科学院 上海天文台,上海 200030)
0 引言
原子钟作为高精度时频信号产生装置,是各时间系统的核心部件,其性能好坏直接影响时间的精度和预报准确度。多年来,对原子钟性能的评估,从时域到频域均提出多种理论和方法[1-2]。对时差比对测量数据产生的各种粗差、间断点、跳变点、无数据段等的预处理方法也形成了较完善的理论[3]。随着卫星导航领域的发展,相继开展了对导航卫星原子钟性能评估和钟差预报的研究[4-5]。对于北斗卫星导航系统(BeiDou navigation satellite system, BDS)的卫星钟,更是进行了长期性能的分析研究[6]。针对目前对国产氢钟性能评估,尤其是对国产氢钟长期在线运行性能评估相对缺乏的现状,本文提出基于国产SOHM-4 型氢钟连续相位比对数据对其性能进行评估的方法,论述了由频率准确度、频率漂移率和频率稳定度指标组成的评估模型,以达到对国产氢钟长期在线运行性能进行精确评估的目的。
1 原子钟性能指标
氢钟性能指标有很多,最常用的有频率准确度、频率漂移率及频率稳定度、本文以频率准确度、频率漂移率和频率稳定度为指标,对氢钟长期运行性能进行精确评估。
1.1 频率准确度
频率准确度描述被测频率或计算频率与频率源标称频率的一致程度。其计算公式为
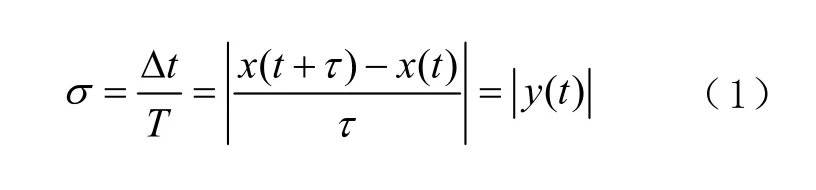
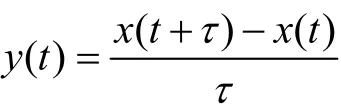
1.2 频率漂移率
频率漂移率描述了原子钟频率随时间发生的单方向变化,其最小二乘法的计算公式为
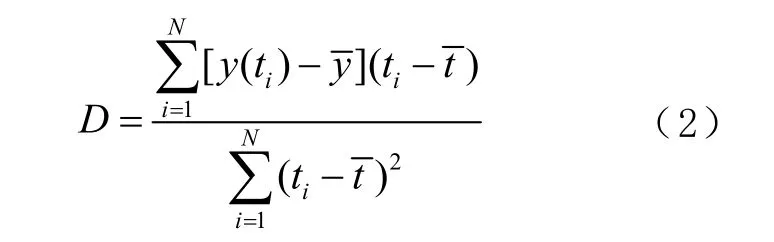
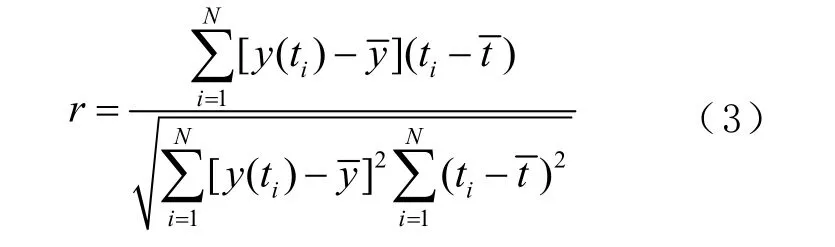
1.3 频率稳定度
频率稳定度是频标输出信号频率不稳定性的衡量标准,一般用阿伦(Allan)方差表征,通过频率数据计算阿伦方差的公式为
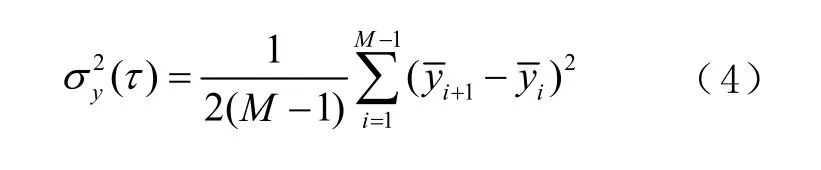
式中:M 为样本总数; τ = mτ0为平滑时间,m 为平滑因子,τ0为基本测量区间;为第i 个平滑时间内m 个频差数据的平均值。
2 评估原理
本文利用2 台国产SOHM-4 型氢原子钟连续运行2 a 多的相位比对数据,对其进行性能评估。在评估过程中,按月对测量数据分组,并利用每组比对数据计算当月原子钟的频率准确度、频率漂移率及频率稳定度数值,最后形成原子钟长期运行的性能评估结果。评估流程如图1 所示,图1 中MAD(median)为中位数。
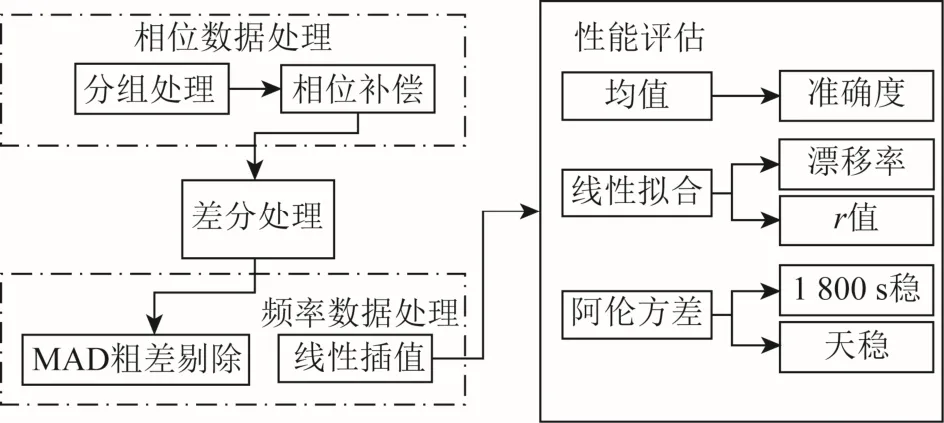
图1 评估流程
2.1 相位数据处理
系统直接测得的氢钟相位比对数据,即时差测量数据,不仅时间跨度较大,而且在长期运行中对原子钟有相位调整操作,测量得到的原始数据并非原子钟在自由运行状态下的比对数据;因此需要进行相位数据处理。
对测量数据按月分组,可以解决时间跨度较大的问题,对于相位调整操作,则可对原始测量数据进行相位补偿操作,其基本原理就是将运行过程中每次相位调整量的负值,补偿回相位调整后所有的时差测量值内。处理流程如图2所示。
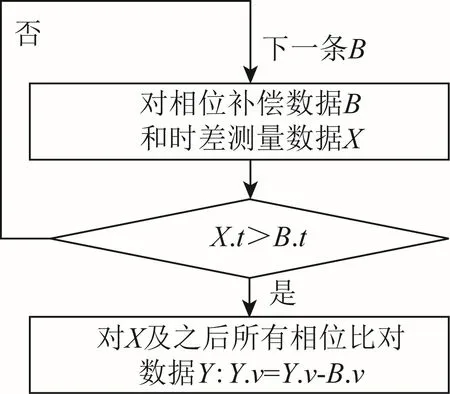
图2 相位补偿流程
图2 中每条相位调整数据B 包含2 个分量:时刻t 和相位调整值v,每条时差测量数据X 也包含2 个分量:时刻t 和相位比对测量值v。B.t 表示取数据B 的t 分量。
2.2 频率数据处理
对时差测量数据进行1 次差分可以得到相对频率偏差数据,也就是钟速。但差分直接得到的频差数据不仅包含无数据段、间断点等测量断点,还可能包含粗差、野值等异常点,无法直接进行评估,因此需要对频率数据进行处理。
对于无数据段,考虑到数据量充足的情况,直接取每月当中连续最长的测量数据段作为当月评估数据。对于粗差、野值等异常点,采用MAD 法[3,7]进行探测,并对探测到的异常点予以剔除。对于间断点和粗差剔除点,采用线性插值法插入。
所谓MAD 粗差探测法,即当频差值满足
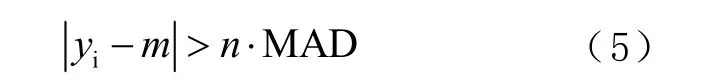
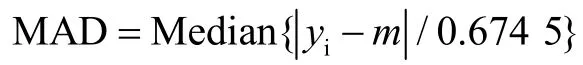
2.3 性能评估
经过频率数据处理,得到连续无间断的频差数据,进一步计算频率准确度、频率漂移率和频率稳定度,得到当月氢钟评估数据。对所有分组进行评估,即得到氢钟长期运行的性能评估结果。
对于频率准确度,采用当月频率偏差绝对值的平均值作为评估值。对于频率漂移率,采用最小二乘法计算,并辅以相关性系数r 表征线性关系强度。对于频率稳定度,分别计算氢钟阿伦方差的1 800 s 稳和天稳作为评估结果。
3 评估结果
待评估氢钟2 a多原始相位比对数据如图3所示。
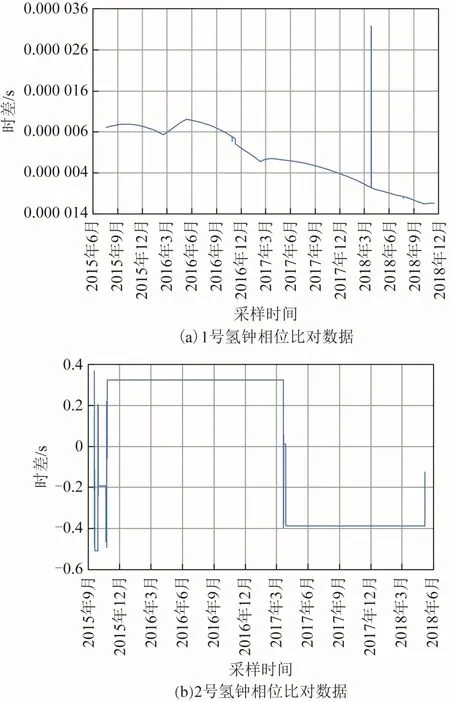
图3 原始相位比对数据
从图3(a)中可以看到,1 号氢钟在2 a 多的长期运行中,除在2016 年上半年出现近4 个月的趋势逆转外,时差测量的变化趋势基本没有较大变化,相位跳变也只在2016 年下半年出现1 次,氢钟性能基本保持稳定。
反观图3(b),2 号氢钟在运行初期即发生部件异常,表现在测量数据上就是2015 年9 月—11 月间时差值发生较剧烈的变化。同时在2017 年上半年,又出现1 次部件异常导致更换部件后零值发生变化,表现在图上就是时差测量值发生较大跳变,导致观测数据分为2 段。这说明2 号氢钟性能相对较差。
3.1 频率准确度评估
2 台氢钟频率准确度计算结果如图4 所示。图4显示,1 号氢钟在长期运行过程中,除3 个月的准确度保持在5.5×10-13左右外,其余时间基本保持在5×10-13之内。而2 号氢钟除运行前5 个月因为部件异常导致频率准确度较大外,在运行近2 a 后,频率准确度亦有所下降,达到1×10-12量级,而中间近1 a 多的长期运行中,频率准确度也基本保持在5×10-13之内。
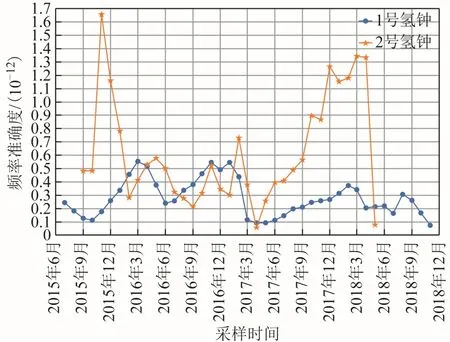
图4 频率准确度评估结果
综合来看,虽然2 号氢钟在整体运行期间,频率准确度数据表现差于1 号氢钟,但长期来看, 2 台氢钟的频率准确度基本优于5×10-13。
3.2 频率漂移率评估
2 台氢钟频率漂移率和相关系数r 的计算结果如图5 所示。
图5 频率漂移率评估结果
图5(a)显示,除2 号氢钟在运行初期的5 个月有异常值外,2 台氢钟的频率漂移率基本处于1×10-14/d 以内,同时1 号氢钟的频率漂移率明显低于2 号氢钟,基本处于0.5×10-14/d 以内,因此可认为氢原子钟长期运行的频率漂移率优于1×10-14/d。
图5(b)显示,2 台氢钟在评估期间的相关系数r 基本处于0.6 以内,这说明氢原子钟的频率漂移率在评估期间并没有呈现明显的线性关系。
3.3 频率稳定度评估
由于测量周期是1 800 s,因此分别计算了1 800 和86 400 s 的Allan 方差,作为对氢钟频率稳定度的评估,计算结果如图6 所示。
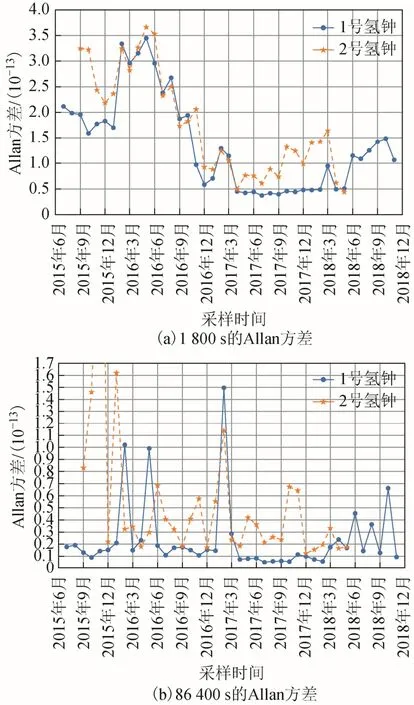
图6 频率稳定度评估
图6(a)显示,2 台氢钟在评估期间的1 800 s稳基本处在5×10-14以上,并且运行初期1 a 内的频率稳定度计算结果明显偏大,1 a 之后则相对稳定,同时明显看出2 号氢钟稳定度差于1 号氢钟。
图6(b)显示,2 台氢钟的天稳在评估期间基本处于1×10-14~2×10-14之间,1 号氢钟除中间3 个异常点外,总体保持在天稳2×10-14以内,且天稳数据上下浮动不大。而2 号氢钟,运行初期的5 个月由于部件异常,频率稳定度计算结果很差,最高甚至超过5×10-13量级(图6(b)中被截断部分),总体天稳数据也明显差于1 号氢钟,但基本在2×10-14以内。
从运行环境来看,导致频率稳定度下降的因素主要有2 个:1)环境温度影响,氢钟标称的工作环境要求温差在±0.5℃内,而实验氢钟所处的实际环境温差变化在±2.5℃左右,温差变化范围扩大,会导致频率稳定度下降;2)相位调整影响,虽然通过补偿算法对调相操作的相位影响作以补偿,但调相操作本身破坏了氢钟自由运行的状态,也会导致氢钟频率稳定度下降。
为进一步分析氢钟的频率稳定性,分别计算了2 台氢钟阿伦方差、重叠阿伦方差、哈德玛方差和重叠哈德玛方差[3]的1 800 s 稳和天稳数据,结果如图7 和图8 所示。
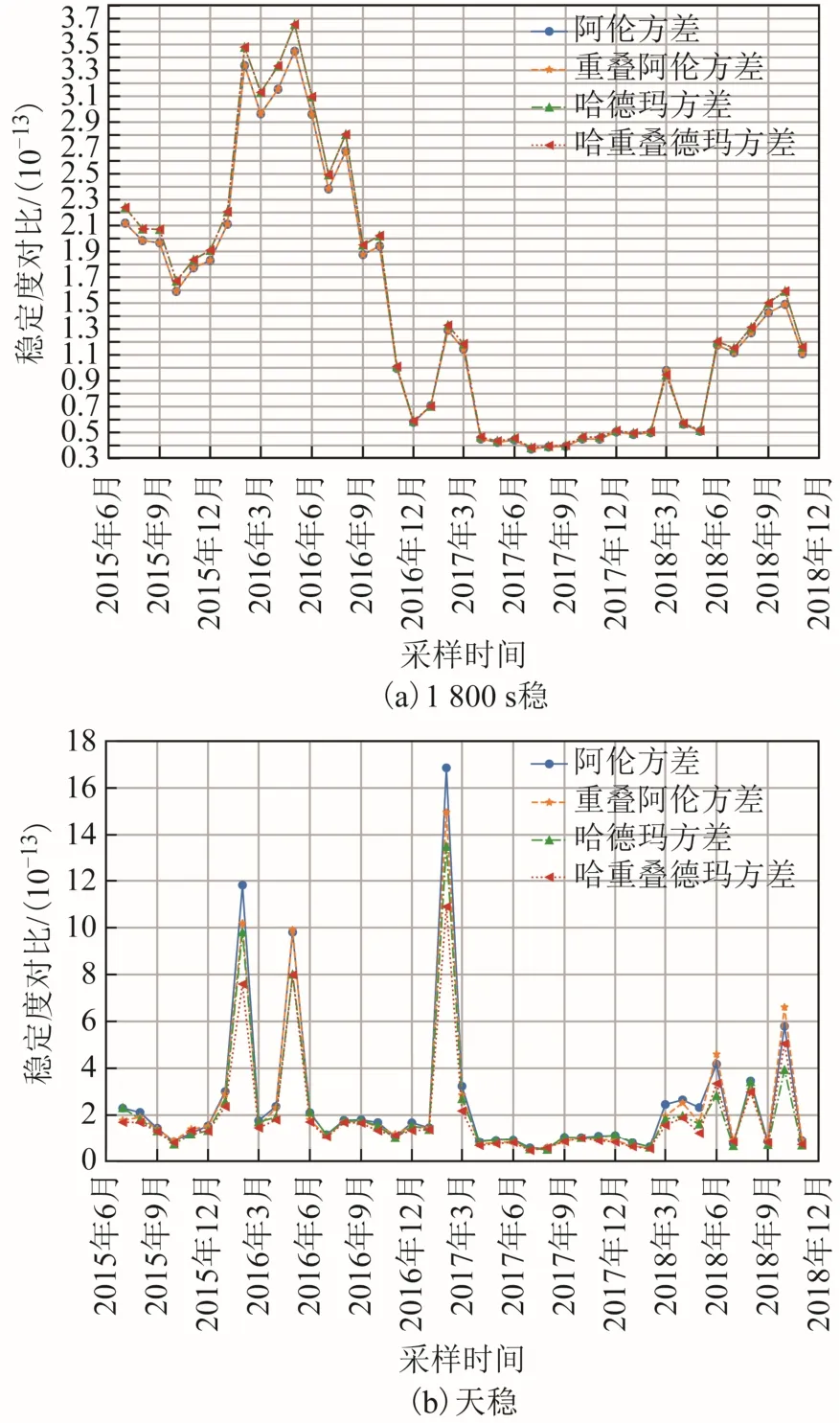
图7 1 号氢钟频率稳定度分析
从图7、图8 的计算结果来看,总体上阿伦方差、重叠阿伦方差、哈德玛方差和重叠哈德玛方差的趋势基本一致,其中阿伦方差和重叠阿伦方差,哈德玛方差和重叠哈德玛方差在大部分的时间范围内数值也基本重合。但是阿伦系方差和哈德玛系方差的趋和程度在时间范围上呈现一定的变化,具体而言,在2 台氢钟运行初期的1 a,氢钟运行的状态尚未固化,阿伦系方差和哈德玛系方差呈现出分离的趋势,而氢钟运行1 a,进入相对稳定的运行状态后,阿伦系方差和哈德玛系方差 又呈现出重合的趋势;从平滑时间来看,1 800 s 稳的重合程度略优于天稳的重合程度,而天稳在分离的趋势上则更明显一些。
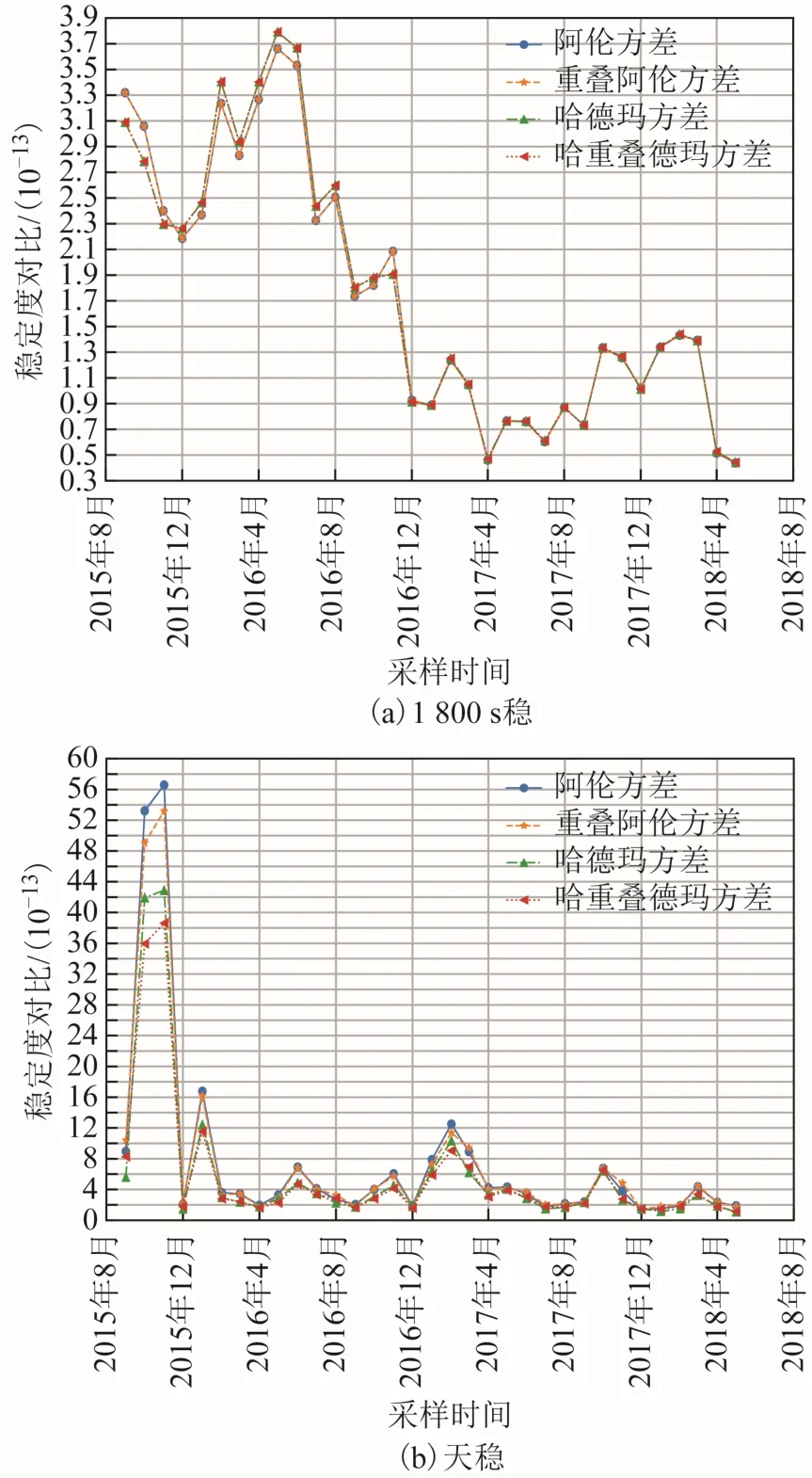
图8 2 号氢钟频率稳定度分析
4 结束语
通过对2 台氢钟长期在线运行性能的评估,可以得到以下结论:
1)在长期连续运行条件下,国产氢钟的频率准确度基本优于5×10-13,频率漂移率优于1×10-14/d且线性关系不明显;
2)氢钟的频率稳定度以天稳计算,由于受到环境温度变化和相位调整的影响,计算结果大概率处于1×10-14~2×10-14之间,并且环境温度的稳定性和自由运行状态的保持性是影响氢钟频率稳定性的重要因素;
3)氢钟在运行初期的1 a 内,频率稳定度计 算结果相对较大,阿伦系方差和哈德玛系方差呈现出分离的趋势,而运行1 a 状态相对固化之后,频率稳定度计算结果变小,且阿伦系方差和哈德玛系方差呈现出重合的趋势。
