GPS 数据处理软件中基线选取方式对解算精度的影响
2020-10-22佟雪佳李建章刘彦军刘江涛
佟雪佳,李建章,刘彦军,刘江涛
(兰州交通大学 测绘与地理信息学院/地理国情监测技术应用国家地方联合工程研究中心/甘肃省地理国情监测工程实验室,兰州 730070)
0 引言
全球定位系统(global positioning system, GPS)广泛应用于控制测量、摄影测量、军事、民用交通导航等各个领域[1]。随着GPS 技术的发展,各种 GPS 数据处理商用软件陆续发布。如天宝(Trimble)公司的TGO、TBC,徕卡(Leica)公司的LGO,华测公司的CGO 以及南方公司的南方GNSS 数据处理软件等。
基线不仅用于后续的网平差,同时可用于检验观测数据的质量以及准确评估GPS 网平差的精度可靠性,因此基线向量的选取很大程度影响着最后的平差精度[2]。
GPS 数据处理软件是否具有自动选取独立基 线的功能,若选取全部基线作为独立基线参与平差计算是否对平差结果有影响,均是研究热点。在以往的数据处理中,大部分用户直接导入全部基线向量进行网平差,但GPS 数据处理软件使用手册并未说明如何选取基线向量。因此,基线向量的选取方式就具有一定的研究价值。
文献[2]通过算例证明,GPS 网平差中的独立基线构网方式解算精度较为真实准确,全部基线网平差的解算精度虚高。在高精度GPS 网平差中,应选择独立基线向量参与平差。文献[3]从理论上证明了在高精度GPS 网平差中,应选择由各同步图形中的独立基线向量构网并作为参与平差的观测量。文献[4]通过2 种选取基线向量方法的对比分析,得出GPS 网平差应选取全部合格基线构网方式,但独立基线构网方式的解算精度较为准确。文献[5]通过实验证明了选取全部的基线作为独立基线,增大了自由度,表面上提高了网平差的精度,造成1 种高精度的假象。
为了保证结果的准确性,本文使用南方全球卫星导航系统(global navigation satellite system, GNSS)等多款数据处理软件进行大量的实验,通过点位精度、中误差、单位权中误差等判断指标来证明进行网平差时,应选取构成闭合图形的独立基线向量作为平差数据。
1 GPS 网平差模型
1.1 3 维无约束平差模型
3 维无约束平差中,GPS 网所采用的观测值均为基线向量(即GPS 基线起点到终点的坐标差)[6]。当有n 台接收机时,1 次同步观测可得n( n- 1)/2条基线向量,其中独立基线( n- 1)条[7-8]。如图1 所示。

图1 GPS 网示意图
假设GPS 网由6 台接收机构成,则全部基线为15 条,独立基线为5 条。令起点Ai和终点Aj的坐标分别为( Xi, Yi,Zi)T、( Xj, Yj,Zj)T,采用Ai、Aj作为观测值列出1 组误差方程为
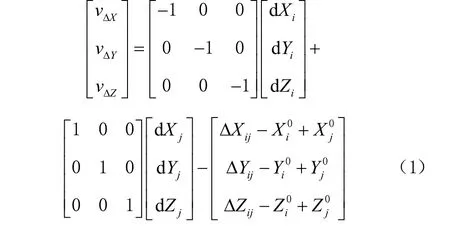

假设在GPS 网中共有n 台接收机,通过观测得到m 条独立基线向量,总的误差方程可写为如下形式(假定第m1条基线向量的2 个端点分别为n1(起点)和n2(终点)),即


在图1 所示的GPS 网中选取其中1 个点作为起算点进行平差计算。基线向量的权阵通常由各基线向量的方差-协方差阵来确定[9]。
按照最小二乘原理进行平差,得到平差结果为
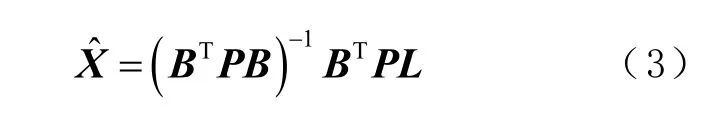
1.2 2 维约束平差模型

若GPS 网由n 台按收机m 条独立基线向量所构成,总的误差方程为

1.3 控制网平差精度指标[7-11]
1)单位权方差为
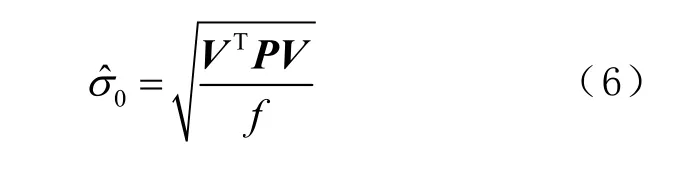
式中:V 为观测值的残差;P 为观测值的权;f 为多余基线数量。观测值的权阵确定时,单位权方差的数值取决于观测值的残差,残差越大,其数值也越大。
2)均方根误差(root mean square, RMS)为

式中:n 为观测值的总数。RMS 为内符合精度指标,其数值小,内符合精度高,反之,则内符合精度差。
3)点位精度
①2 维点位精度为

②3 维点位精度为

式中:Mx、My和Mz分别表示x、y、z 轴的误差。
点位精度就是x 轴和y 轴方向(或x 轴、y 轴和z 轴)的误差平方和的平方根。点位精度用来评定点的离散程度,数值越小说明点的离散程度越小,精度越高。
2 实验与结果分析
为了保证结果的准确性,本文采用以下3 种基线选取方式进行验证:
1)选取全部基线向量;
2)选取独立闭合基线向量(构成闭合图形的独立基线向量);
3)选取独立不闭合基线向量(不构成闭合图形的独立基线向量)。
本文以南方GNSS 数据处理软件和华测CGO数据处理软件为例进行验证。
2.1 南方GNSS 数据处理软件中基线选取方式对解算精度的影响
采用南方GNSS 数据处理软件结合某GPS 控制网(称为控制网1)9 个时段,采样间隔均为30 s 的基线观测数据进行验证。某GPS 控制网每个时段由4 台接收机构成,共有22 台接收机,全部基线54 条,独立基线27 条。
2.1.1 不同基线选取方式对3 维无约束平差精度的影响
1)点位精度对比。点位精度是用来评定点的离散程度,数值越小说明点的离散程度越小,精度越高。点位精度是通过网平差来体现的[12],如图2、表1 为南方GNSS 数据处理软件通过3 维无约束平差解算得到的点位精度。

图2 控制网1 的点位精度统计

表1 控制网1 的点位精度统计
从图2、表1 中可以得到以下结论:
①独立基线与全部基线点位精度相差较大,仅从点位精度可以看出,全部基线网平差后的点位精度要优于独立基线的点位精度,但在对坐标值影响不大的情况下,可以得出全部基线网平差的精度偏高;
②由于独立不闭合基线的点位精度较差,在进行网平差时应选取构成闭合图形的独立基线向量。
2)中误差对比。中误差是在进行基线检验时需要用到的1 个重要参数[13]。图3、表2 为南方GNSS 数据处理软件通过3 维无约束平差解算得到的中误差。

图3 控制网1 的中误差统计

表2 控制网1 的中误差统计
从表2 和图3 可以看出,虽然3 种选取方式得到的中误差差异较小,但是选取全部基线方式的中误差数值最小,选取独立不闭合基线方式的中误差数值最大,由此可得到以下结论:
①由于对坐标值影响不大,选取全部基线向量进行网平差时,精度是偏高的;
②由于选取独立不闭合基线方式的中误差精度较差,在选取独立基线的前提下,应选取构成闭合图形的独立基线向量。
3)单位权中误差对比。当观测值的权阵确定时,单位权中误差的数值取决于观测值的残差,总体上看,残差越大,其数值也越大[14]。表3 为南方GNSS 数据处理软件通过3 维无约束平差解算得到的单位权中误差。

表3 控制网1 的单位权中误差统计表 单位:m
从表3 可以看出独立基线的网精度较低,方差值偏小。
4)基线向量残差对比。基线向量残差是1 项评定基线解算结果质量的重要控制指标[15]。表4、图4 为南方GNSS 数据处理软件通过3 维无约束平差解算得到的基线向量残差。

表4 残差对比统计表

图4 控制网1 的不同方向残差统计
从表4 和图4 可以看出,选取全部基线方式下的改正数绝对值几乎全部大于独立闭合基线,所以应选取独立基线向量进行网平差。因没有检核条件,独立不闭合基线改正数大部分为0,不具有可靠性。因此,在选取独立基线时,应选取构成闭合图形的独立基线向量。
2.1.2 不同基线选取方式对2 维约束平差精度的影响
RMS 主要是用来反映观测值质量的优劣,即观测值与参数估值间的符合程度,RMS 小,内符合精度高,反之,内符合精度差[16]。表5、图5 为南方GNSS 数据处理软件通过2 维约束平差解算得到的RMS 和点位精度。
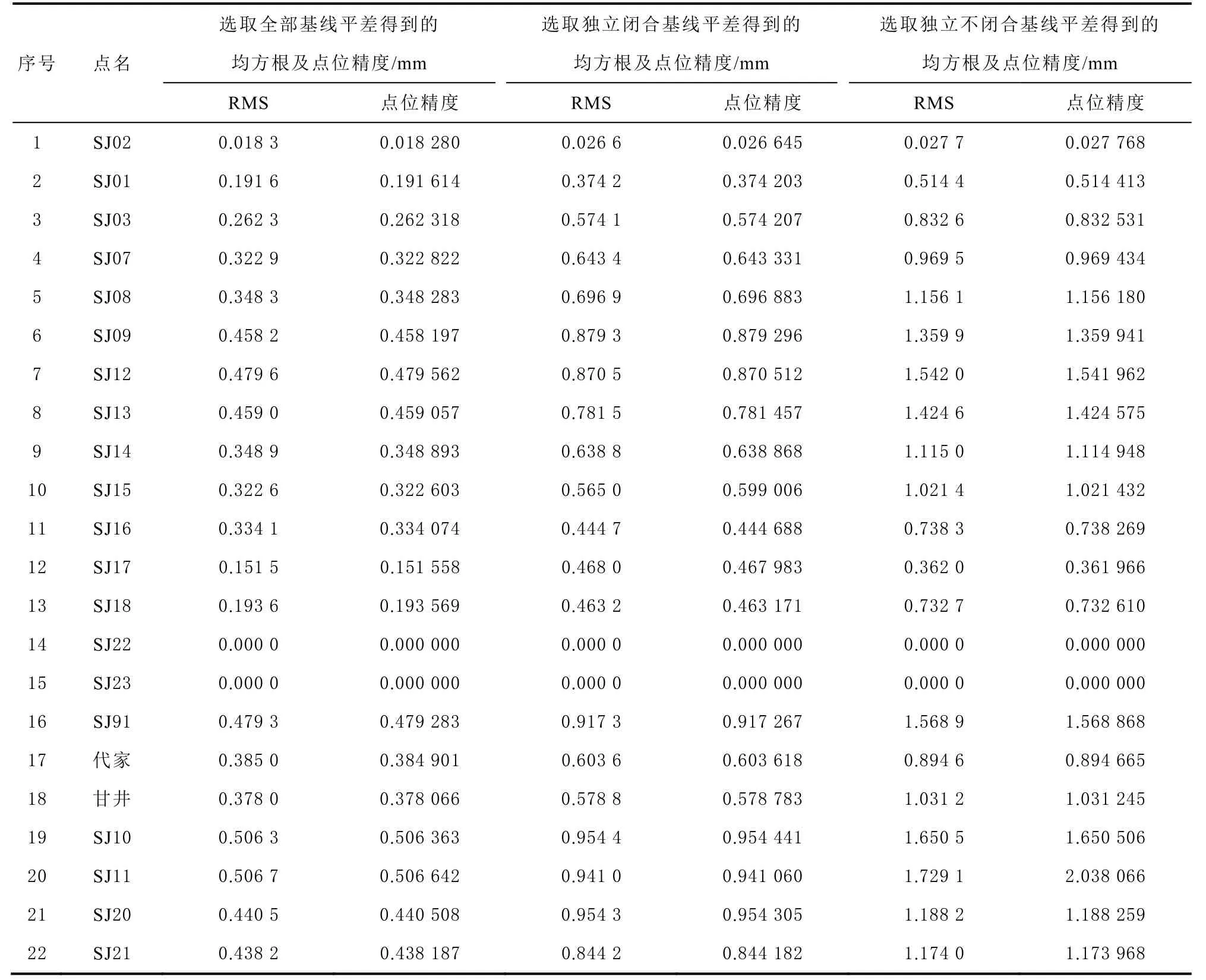
表5 控制网1 的RMS、点位精度统计表

图5 控制网1 的RMS、点位精度统计
从表5 和图5 可以看出,3 种基线向量选取方式进行2 维约束平差后,得到的解算精度差异明显,从图5 可以得出以下结论:
1)由于对坐标值影响不大,选取全部基线向量进行网平差时,精度是偏高的;
2)由于独立不闭合基线平差后的精度较差,应选取构成闭合图形(如大地四边形、三角形)的独立基线进行网平差[17]。
2.2 华测CGO 数据处理软件中基线选取方式对解算精度的影响
CGO 数据处理软件结合神木某铁路4 个时段且采样间隔均为30 s 的基线观测数据(称为控制网2)进行验证。神木某铁路每个时段由4 台接收机构成,共有10 台接收机,全部基线24 条,独立基线12 条。
2.2.1 不同基线选取方式对3 维无约束平差精度的影响
1)点位精度对比。图6、表6 为华测CGO 数据处理软件通过3 维无约束平差解算得到的点位精度。

图6 控制网2 的点位精度统计图
从图6 中可以得到以下结论:
①全部基线网平差后的点位精度优于独立基线的点位精度,但在对坐标值影响不大的情况下,可以得出全部基线网平差的精度偏高;②由于独立不闭合基线的点位精度较差,在进行网平差时应选取构成闭合图形的独立基线向量。 2)单位权中误差对比。表7 为华测CGO 数据处理软件通过3 维无约束平差解算得到的单位权中误差。
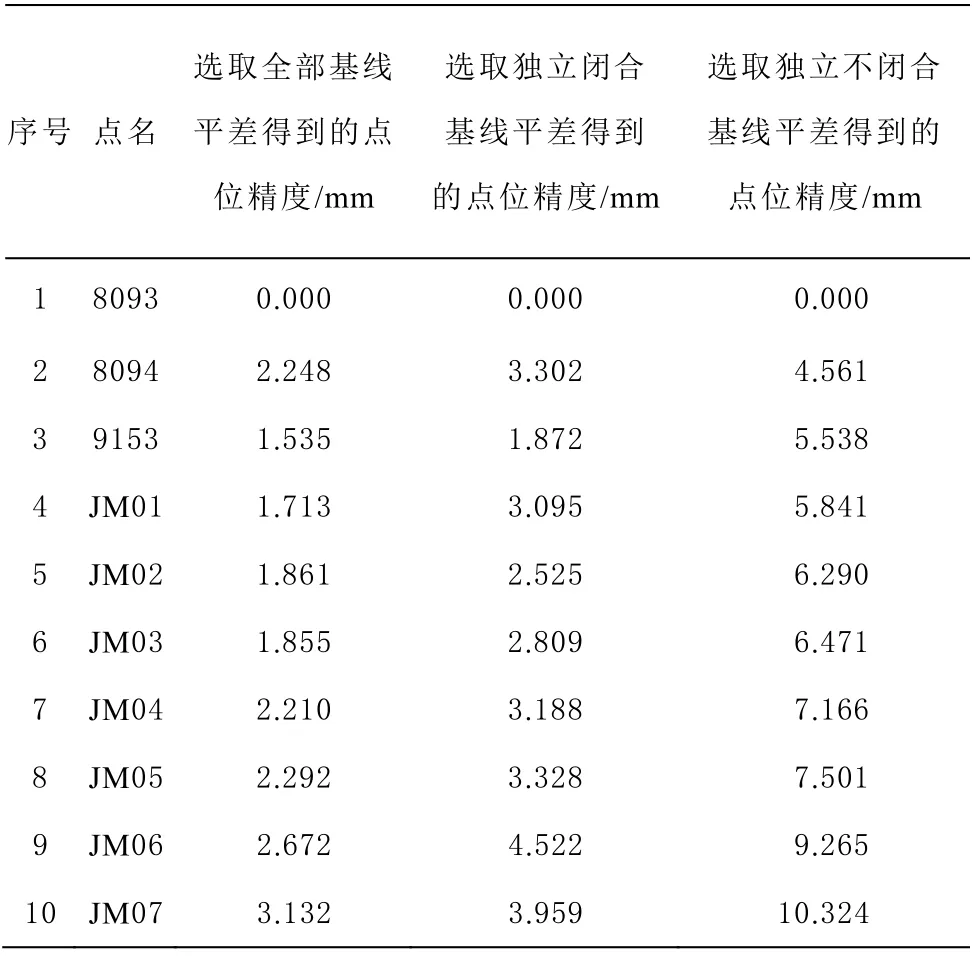
表6 控制网2 的点位精度统计

表7 控制网2 的单位权中误差统计 单位:mm
从表7 可以看出独立闭合基线的网精度较低,方差值偏小。
3)基线向量残差对比。表8、图7 为华测CGO数据处理软件通过3 维无约束平差解算得到的基线向量残差。根据表8 和图7 可以看出,选取全部基线方式下的改正数绝对值几乎全部大于独立闭合基线,所以应选取独立基线向量进行网平差。因没有检核条件,独立不闭合基线改正数大部分为0,不具有可靠性。因此,在选取独立基线时,应选取构成 闭合图形的独立基线向量。
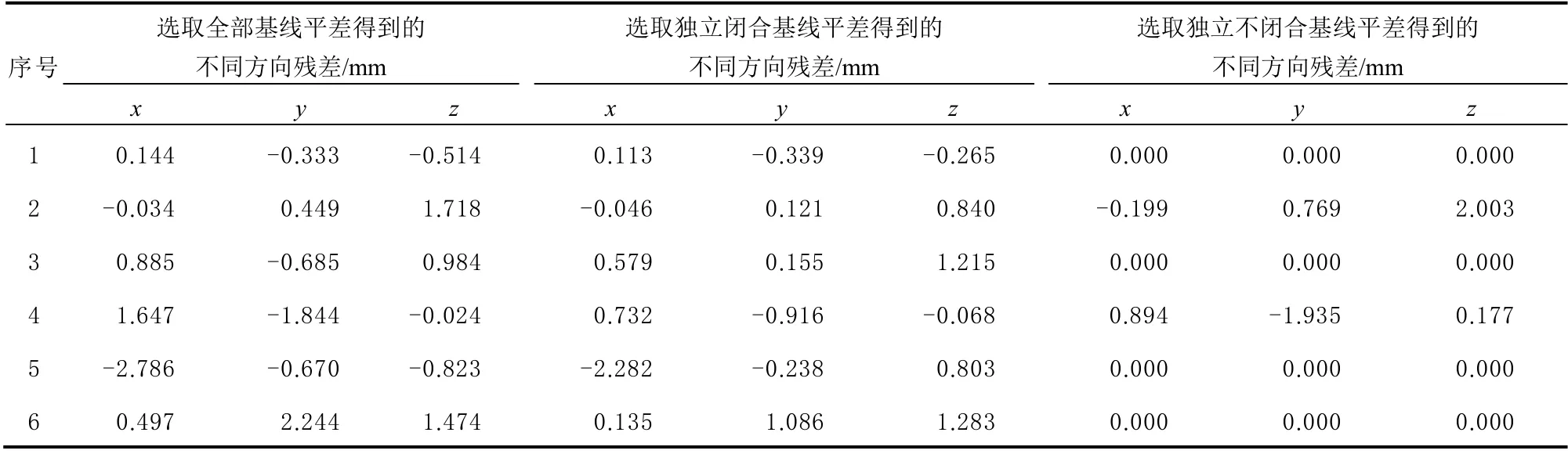
表8 控制网2 的残差对比统计

图7 控制网2 的不同方向残差统计
2.2.2 不同基线选取方式对2 维约束平差精度的影响
表9、图8 为华测CGO 数据处理软件通过2 维约束平差解算得到的点位精度。

表9 控制网2 的点位精度统计表
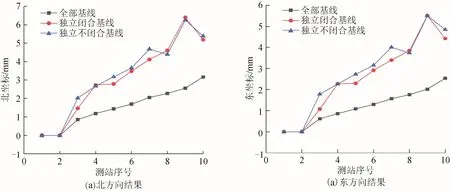
图8 控制网2 的不同方向点位精度统计
表9 和图8 与表5、图5 类似,结论一致。通过以上的实验说明,虽然独立基线向量的网平差精度较差,方差值偏小,但是选取独立基线向量构网方式反映的 GPS 网平差精度较为真实准确。由此可得出,全部基线向量参与网平差时精度虚高,存在失真现象。因此,在GPS 规范中特别强调选取独立基线向量进行网平差。
3 结束语
本文基于多组实测数据,通过网平差解算精度,分析比较了南方GNSS 数据处理软件和CGO 软件3 种不同基线选取方式之间的差异,由实验可知:
1)现有的工程数据处理软件没有自动选取独立基线的功能,必须采用人工构网方式;
2)GPS 控制网内部精度高低,不仅受基线质量的影响,同时受多余基线数量的影响。因此,在GPS 网平差中,独立基线向量构网方式的观测精度较为准确,全部基线向量构网方式的平差精度,只是造成了高精度的假象;
3)南方GNSS 数据处理软件和CGO 软件进行网平差时应选取构成闭合图形(如大地四边形、三角形)的独立基线向量;
4)在粗差存在的情况下,由于全部基线向量网平差解算精度虚高,会导致误判。
