契合点 落脚点 生长点
——数学教学“错误”资源运用策略探析
2020-10-21许素玉
许素玉
(华安县第二实验小学,福建 华安 363800)
“在数学教学活动中,‘错误’往往是教师在教学中和学生在学习过程中,反映在各方面,出现违反教学结论或数学方法的现象。”[1]当学生出现错误时,有些教师不知所措,甚至以一个“错”字叫停学生,殊不知这样既打断学生的思维,也浪费了难得的课堂生成资源。《义务教育数学课程标准(2011 年版)》明确指出:在数学教学过程中恰当地使用“错误”资源,将在很大程度上提高学生从事数学活动的水平和教师从事教学活动的质量。
一、发现“错误”,架设新旧知识契合点
在数学学习中,新旧知识之间的联系是密切的。正因为数学知识的连贯性,教学时,大多教师都会把教学设计的重心放在新旧知识的沟通关联上,让学生通过与教材、教师、同伴的一次次对话发现错误,进而分析错误、纠偏错误,实现对所学新知识的获取,充分体验“错误中往往孕育着比正确更丰富的发现和创造因素”。例如,教学人教版小学数学五年级上册“平行四边形的面积计算”这一课时,学生已经理解并能熟练计算长方形和正方形的面积,不管是长乘宽,还是边长乘边长,学生印象中构建的是“两条邻边长度相乘的积”这一数学模型。上课伊始,教师用课件展示一块平行四边形菜地(如图1),要求学生尝试计算菜地的面积。

图1
受之前的面积计算的影响,有的学生脱口而出:5×4=20(平方米);有的学生发现多了3.2m,认为答案应该没有那么简单。这时,要求学生拿出课前制作好的长5cm、宽4cm 的可拉伸长方形学具。通过拉动对角,长方形慢慢变成了平行四边形,并且越拉越扁,即高越来越小,面积也跟着变小了。但是在这个拉动过程中,相邻两条边的长度始终没有发生变化。显然,拉动之后所得到的平行四边形的面积一定比长方形的面积小,那么面积到底是多大呢?学生展开合作学习:一割补:把平行四边形沿着高剪开,平移转化成一个长方形;二观察:发现平行四边形与转化后的长方形面积相等,长方形的长与平行四边形的底相等,长方形的宽与平行四边形的高相等;三推导:得到“平行四边形的面积=底×高”这一计算方法。
教师及时捕捉到关键性的错误,重新整合出新的学习资源回馈给学生,并让学生在自主探究、合作交流中找寻“错误”与“正确”之间的内在联系,构建起牢固的知识体系,为学生深度探究注入强大动力。[2]教师若在导入过程中发现“错误”资源,架设新旧知识契合点,既能提升学生知识与技能的转化能力,又能培养学生自主合作探索知识的能力。
二、挖掘“错误”,夯实生成知识落脚点
布鲁纳说:“学生的错误都是有价值的。”面对学生在学习中所暴露出来的错误,教师应予以宽容,并以独到的视角对其价值进行重新定位,进而引领学生深入挖掘错误价值,在试错中充分地探究、思考。[1]例如,教学人教版小学数学二年级上册“两位数加减两位数(不进位)”例1:35+2=?后,学生已经理解掌握“个位要和个位对齐”的计算道理,接着出示例2:35+32=?,似乎没有难度,“十位也要和十位对齐,也就是相同数位要对齐。”这一计算法则水到渠成。可是真正落实到计算时,很多学生又茫然无措。当教师要求学生计算6+32=?时,出现两种不同答案:①6+32=92,②6+32=38。
生1:用小棒摆,先摆6 根小棒表示6 个一,加上32就是摆3 捆又2 根小棒,表示3 个十和2 个一,合起来就是3 个十和8 个一,得38。(如图2)
生2:用计数器拨珠,在个位上拨上6,接着加上32,3 个十就要在十位上拨3,个位上拨2,也得38。(如图3)
生3:6+32,6 表示6 个一,2 也表示2 个一,表示6个一的6 不能和表示3 个十的3 相加,所以个位上的6应该和个位上的2 对齐,也得38。

图2
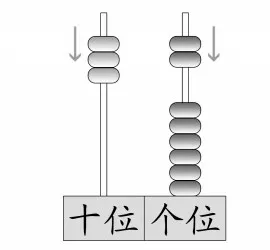
图3
教师为学生提供争论的时间和空间,引导他们从正反不同角度去修正错误,让学生在争论中分析,在争论中明理,在争论中内化知识,在聆听与思考中轻松突破计算两位数加一位数时,首先要注意“相同数位对齐”这个知识难点,提升逻辑思维与推理能力、抽象与运用能力。
三、诱发“错误”,拓宽运用知识生长点
课标指出,数学知识的教学是一个整体,而不是“碎片化”的单一的一节课的教学,教师要关注知识的“生长点”与“延伸点”,要处理好局部知识与整体知识的关系。为此,可以打破传统的课后巩固模式,设置一些操作性强、富有挑战性的问题,诱发“错误”,引领学生在大胆猜测、动手验证、交流分享的过程中,化“错误”为“正确”,感受从不同角度、不同层次理解思考问题的价值。
例如,教学人教版小学数学六年级下册“圆柱的表面积”一课后,教师在延伸环节设计一道题:给圆柱形切一刀,会有什么变化?受本课知识点的暗示,有学生说:“表面积减少了。”教师要求学生动手试一试,拿出课前准备的各种“道具”:圆柱形的萝卜、地瓜、卡纸做的模型、罐子等。学生有独自动手,有三五扎堆,或剪或切,接着表达自己的发现:①平行于底面切一刀,表面积增加了,增加的是两个底面积之和(如图4);②垂直于底面切一刀,表面积增加了,增加的是两个长方形的面积之和,其中每个长方形的长相当于圆柱底面直径,宽相当于圆柱的高(如图5);③用剪刀垂直与圆柱的底面剪一刀,再把侧面剪开,展开后得到一个长方形,长方形的长与圆柱的底面周长相等,宽与圆柱的高相等,长方形的面积就是圆柱的侧面积(如图6);④用剪刀在圆柱的侧面斜着剪一刀,展开后得到一个平行四边形,平行四边形的底正好等于圆柱的底面周长,高正好等于圆柱的高,平行四边形的面积正好等于圆柱的侧面积(如图7)。

通过学生的动手操作、用心思考,以及教师适时点拨,把师生的有效互动引向纵深,使数学课堂成为思维碰撞和交锋的舞台,促进数学课堂教学的不断生成和发展。[3]若教师常在知识运用生长点诱发“错误”,拓宽知识运用渠道,则学生开放性思维、逻辑推理思维、空间想象思维等都能得到锻炼与培养。
