基于信息匹配度的混合推荐算法

任静霞，武志峰

（天津职业技术师范大学信息技术工程学院，天津 3002222）

推荐系统[1]是大数据背景下，降低信息过载、帮助服务商精准提供用户所需信息的一种解决方案，被广泛应用于各大电子商务网站。推荐系统利用收集到的用户喜好或者物品信息特性等进行训练，得到用户-物品推荐模型，从而预测用户未来可能会感兴趣或者需要的物品，为用户提供定制化服务。实现推荐系统的推荐算法有协同过滤推荐算法、基于内容的推荐算法、基于知识的推荐算法、基于关联规则的推荐算法等，其中协同过滤算法（collaborative filtering，CF）使用最为广泛，但是冷启动问题无法得到解决，在稀疏矩阵中性能下降，可扩展性差；基于内容的推荐算法要求内容能够容易抽取成有意义的特征，并且要求特征内容有良好的结构性，但其可解释性差；而基于知识的推荐算法存在知识难以获取的问题，要求用户需求明确且需求具有可推荐性。正因为以上算法均有不足之处，所以研究者们一直致力于追求适应性更强、推荐质量更高的推荐算法。

为提高推荐质量获得较好的推荐结果，前人做了大量研究。如冷亚军等[2]对协同过滤技术进行了总结；饶钰等[3]通过融合评分向量间余弦值和均方差值改进协同过滤算法；Koren 等[4]对推荐系统中现有的矩阵分解技术进行了分析综述；王娟等[5]提出将矩阵分解的结果应用于基于用户的最近邻推荐；刘沛文等[6]将不同用户对于不同物品的个性化行为特征指数引入相似度的计算中；李鹏飞等[7]将物品属性相似性和改进的修正余弦相似性线性组合作为相似性度量方法；苏晓云等[8]提出一种基于动态加权的混合协同过滤算法，考虑了项目近邻和隐藏特征这2 个因子并进行权重计算，提高推荐精度。本文在传统推荐方法的基础上，提出了一种新的基于推荐信息匹配度的协同过滤和矩阵分解的动态权重混合算法（UIBCF-MF），该算法根据某一用户和物品的近邻推荐与已有信息的不匹配度动态调整权重，与传统单个算法相比，既能发挥各算法优势，又能改善其准确性和可扩展性。

1 协同过滤算法

协同过滤算法[9]采用 K 近邻（k-nearest neighbor，KNN）技术，从用户角度出发，通过用户的历史喜好信息分析各个用户之间的相似度或者物品之间的相似度，然后利用目标用户的最近邻用户，或是目标物品的最近邻物品，以其对商品评价的加权评价值来预测用户对特定商品的喜好程度，系统根据这一喜好程度进行推荐。协同过滤算法依赖于准确的用户评分，计算过程中热门商品被推荐几率更大，存在冷启动问题，无法对新用户或物品进行处理，不适用于生存周期短的物品。协同过滤算法分为基于用户的协同过滤（user-based CF）和基于物品的协同过滤（item-based CF）[10]2 种。

1.1 基于用户的协同过滤

user-based CF 适用于用户交互性强或者用户数量相较物品数量变化较稳定的情况。定义推荐系统中，U={u1，u2，…，um}为 m 个用户的集合，I={i1，i2，…，in}为n 个物品的集合，R[m×n]为用户-物品评分矩阵，rui为用户 u 对物品 i 原始评分值为用户 u 对物品 i预测评分值，user-based CF 所得预测评分为

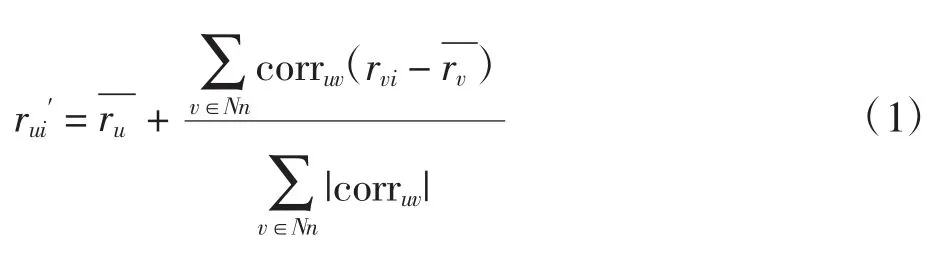
1.2 基于物品的协同过滤

item-based CF 适用于物品数量变化明显小于用户数量变化的情况。定义推荐系统中，U={u1，u2，…，um}为 m 个用户的集合，I={i1，i2，…，in}为 n 个物品的集合，R[m ×n]为用户-物品评分矩阵，rui为用户 u 对物品i 原始评分值为用户u 对物品i 预测评分值，item-based CF 所得预测评分为

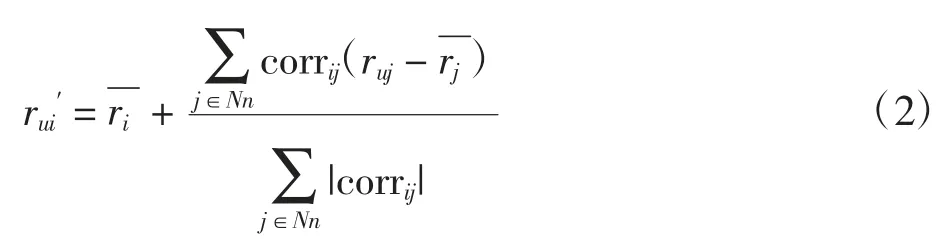
1.3 相似度计算

适用于推荐系统的相似性度量方法有很多，使用较多的有皮尔逊相关系数、余弦相似度和欧式距离等。

1.3.1 皮尔逊相关系数

计算公式

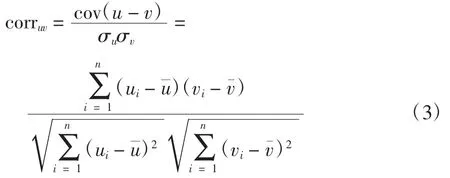
式中：corr 为相关系数，值在[-1，1]，corr=0 时，u、v 不相关；|corr|越大，u、v 相关性越强。

1.3.2 余弦相似度

计算公式

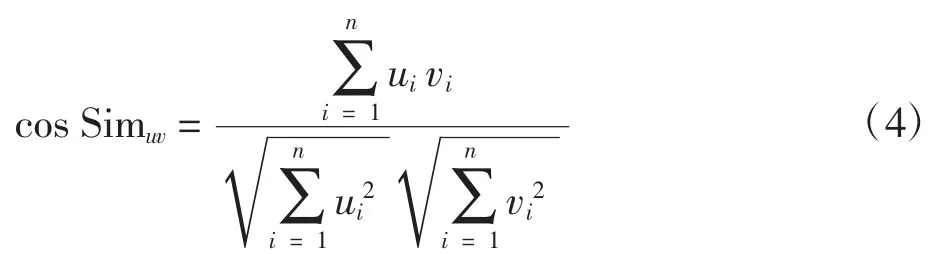
式中：cos Sim 为 u、v 间相似度。

1.3.3 欧氏距离

计算公式

式中：d 为 u、v 间欧氏距离。

2 矩阵分解算法

矩阵分解算法（matrix factorization，MF）[11-12]是基于模型的推荐算法中的一种，通过将历史用户-物品信息矩阵进行分解，再用分解后的矩阵预测未知评分，从而完成推荐。矩阵分解很好地解决了评分数据稀疏性问题，易于编程实现，具有可扩展性，但其模型训练过程耗时较长且解释性不强。

2.1 矩阵分解模型

定义推荐系统中，U={u1，u2，…，um}为 m 个用户的集合，I={i1，i2，…，in}为 n 个物品的集合，R[m × n]为用户-物品评分矩阵，将矩阵R 分解为2 个矩阵Pm×k和Qk×n的乘积，Rm×n≈Pm×k× Qk×n=R′，其中，矩阵 P 为用户隐含特征矩阵；矩阵Q 为物品隐含特征矩阵为用户u 对i 物品预测评分值。MF 所得预测评分为

式中：p、q 分别由矩阵 P、Q 经随机梯度下降算法得到。

2.2 随机梯度下降算法

随机梯度下降算法是机器学习较常见的一种优化算法。将原始评分矩阵R 和重新构建的评分矩阵R′之间误差的平方作为损失函数[13]，利用梯度下降法求解损失函数最小值，为了获得较好的泛化能力，在损失函数中加入正则项，得到损失函数

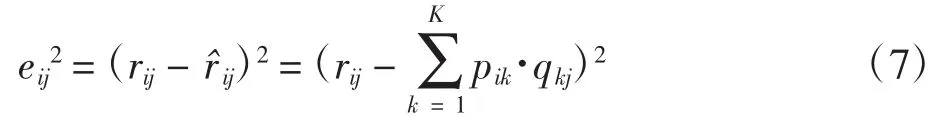
损失函数负梯度为

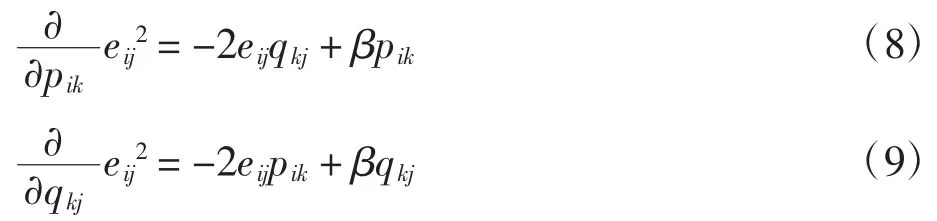
得到更新变量公式

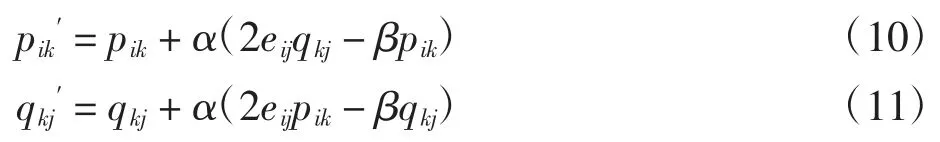
通过迭代，直到算法收敛，得到p、q。

3 UIBCF-MF 算法

算法首先采用单一传统user-based CF、item-based CF 和MF 推荐算法进行评分预测，再根据3 种算法所得预测评分与历史数据间不匹配度动态调整各算法权重从而实现最终评分预测，针对冷启动问题采用二次矩阵分解办法。算法分为3 个部分：①通过KNN计算预测评分时提出的一种新的主观评分规范化方法；②针对不同情况下的3 种推荐算法进行加权混合；③当新用户或新物品出现时采用冷启动处理方法。

3.1 主观评分规范化

在进行传统user-based CF 和item-based CF 评分预测时，考虑到邻居用户或物品与目标用户或物品的评分习惯不同造成的评分差异，在使用皮尔逊相关系数计算相似性，通过最近邻进行评分预测时，提出一种适用于不同评分区间的评分规范化方法。以基于用户的最近邻为例，定义用户v 对用户u 影响因子为fv，则 user-based CF 所得预测评分 rui′为

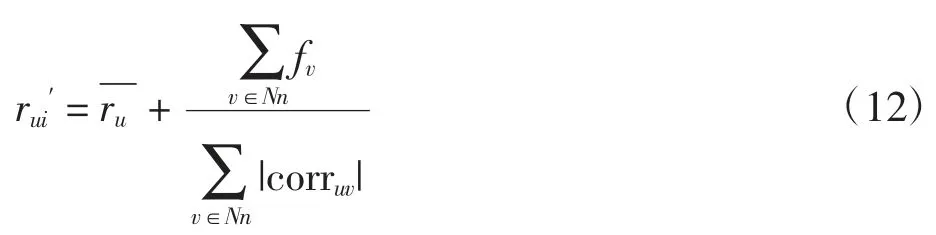
进行评分规范化的评分预测步骤如下。

输入：原始用户-物品评分rui，用户或物品近邻列表。

输出：用户v 对用户u 影响因子fv。

步骤1 评分区间为[rmin，rmax]，计算用户u 与近邻用户v 间相关系数corruv。

步骤 2 若 corruv＞ 0，则为正相关，fv值由式（13）求得；反之，若 corruv＜ 0，则为负相关，fv值由式（14）求得

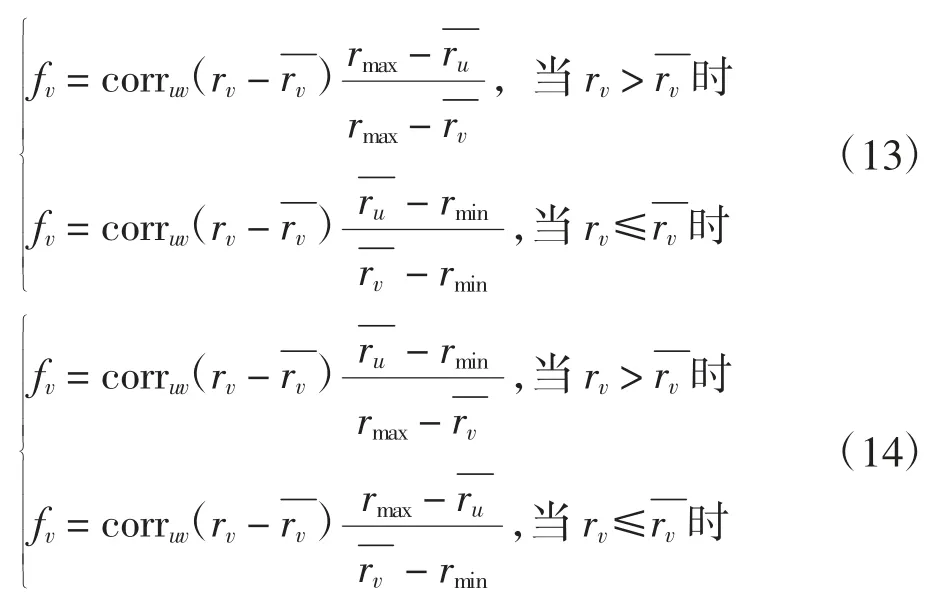
3.2 加权混合预测

定义R[m×n]为原始用户-物品评分矩阵，rui为用户u 对物品i 原始评分值，由user-based CF、item-based CF 和MF 算法得到预测评分矩阵R1[m×n]、R2[m×n]和 R3[m × n]、r1ui、r2ui、r3ui分别为矩阵 R1、R2、R3 中用户u 对物品i 评分，经加权混合算法得到最终评分预测矩阵R4[m × n]，其中用户u 对物品i 评分值为r4ui。

算法思想：对于评分矩阵中每一个评分r，计算user-based CF，item-based CF 和 MF 3 种算法所得预测评分r 与原始评分rui匹配度，从而动态调整权重。若原始评分rui不为空而某一算法预测评分为空，则认为该算法推荐不合理，调整各算法对该评分值影响，降低该算法影响度；若存在多个合理推荐值，则根据匹配度择优选择。

混合算法步骤如下。

输入：原始用户-物品评分rui，基于用户的协同过滤预测评分r1ui，基于物品的协同过滤预测评分r2ui，矩阵分解预测评分r3ui。

输出：加权混合预测评分r4ui。

步骤1 根据输入的评分，定义w1、w2、w3 为加权因子，len为物品数，当rui值不为空时，统计r1ui空值个数 a，r2ui空值个数 b。

步骤2 若rui值为空，执行步骤3，否则执行步骤6。

步骤3 若r1ui值为空，执行步骤4，否则执行步骤5。

步骤4 若r2ui值为空，r4ui=r3ui，结束算法。否则w1r1ui+w2r2ui+w3r3ui，结束算法。

步骤5 若r2ui值为空结束算法。否则结束算法。

步骤6 若r1ui值为空，执行步骤7，否则执行步骤8。

步骤7 若r2ui值为空，r4ui= r3ui，结束算法。否则选择 |r2ui-rui|与|r3ui-rui|较小值赋给r4ui，结束算法。

步骤 8 若 r2ui值为空，选择|r1ui-rui|与|r3ui-rui|较小值赋给r4ui，结束算法。否则选择|r1ui-rui|、|r2ui-rui|与|r3ui-rui|较小值赋给r4ui，结束算法。

3.3 冷启动问题

在推荐系统中，传统user-based CF 和item-based CF 算法利用已有历史数据构建推荐模型，故当新用户或新物品出现时，算法无法给出相应推荐，冷启动问题无法解决。UIBCF-MF 算法利用MF 算法能有效解决冷启动问题这一思路解决上述问题，解决方式如下。

对于用户冷启动，提出新用户，对提取后剩余的待测数据 R[m′× n]使用 user-based CF、item-based CF和MF 算法进行评分预测分别得到评分矩阵R1[m′×n]、R2[m′× n]和 R3[m′× n]，通过 UIBCF-MF 算法中混合加权方法得到预测结果矩阵R4[m′× n]，添加已提出新用户数据到该矩阵得到矩阵R4′[m×n]，并使用MF 算法进行二次矩阵分解得到最终预测结果矩阵R4[m × n]。

对于物品冷启动，提出新物品，对提取后剩余的待测数据 R[m × n′]使用 user-based CF、item-based CF和MF 算法进行评分预测分别得到评分矩阵R1[m×n′]、R2[m × n′]和 R3[m × n′]，使用 UIBCF-MF 算法中混合加权方法得到预测结果矩阵R4[m×n′]，添加已提出新用户数据到预测结果矩阵得到矩阵 R4′′[m × n]，使用MF算法进行二次矩阵分解得到最终预测结果矩阵R4[m × n]。

算法冷启动解决伪代码如下。

Begin

输入 待测数据A，训练数据B

IF A 中用户或物品集a∈B 中用户或物品集b 执行

Step1：将测试数据进行UIBCF-MF 加权混合预测ELSE执行

Step2：提出 A 中满足 a[i]∉b 冷数据

Step3：将提出后的待测数据进行UIBCF-MF 加权混合预测

Step4：添加已提出数据a[i]到预测结果矩阵，使用MF 算法进行评分预测

End

4 结果与分析

4.1 评价标准

实验使用均方根误差（rootmeansquareerror，RMSE）和平均绝对误差（mean absolute error ，MAE）[13-14]作为算法评价指标。计算公式为

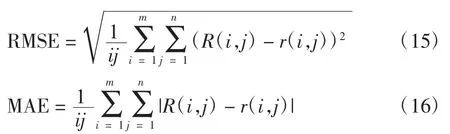
4.2 实验结果

实验所用数据集为Grouplens 提供的MovieLens数据集中943 位用户对1 682 部电影的最新评分，共计100 000 条，评分范围为0~5 分，其中每位用户至少拥有20 条评分，数据集极其稀疏，稀疏度为0.936 9。实验将数据集按照8 ∶2 分为训练集和测试集[15]。

本文设置了3 组对比实验，第1 组实验为固定MF 算法所得预测矩阵，当近邻数Nn 不同时，传统单一的user-based CF 算法、item-based CF 算法与本文提出的UIBCF-MF 算法的实验结果对比，user-based CF、item-based 与 UIBCF-MF 的 RMSE 及 MAE 比较分别如图 1 和图 2 所示[16]。

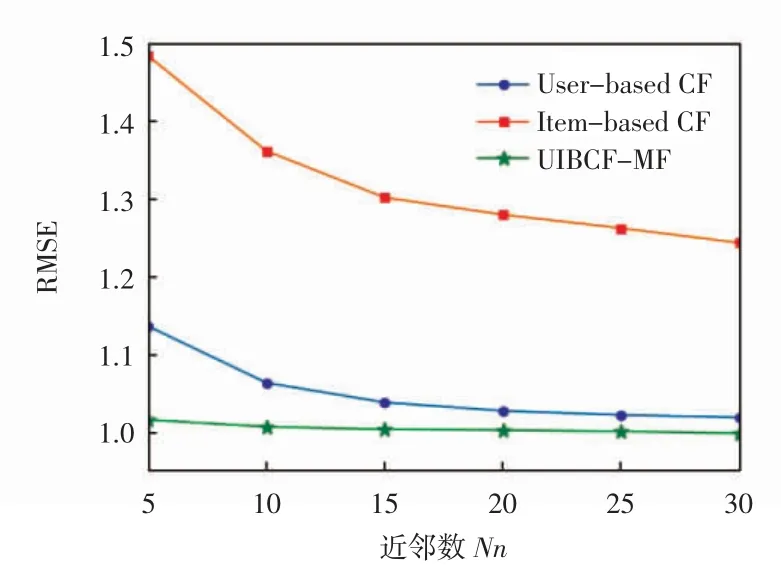
图 1 user-based CF、item-based 与 UIBCF-MF 的RMSE 比较

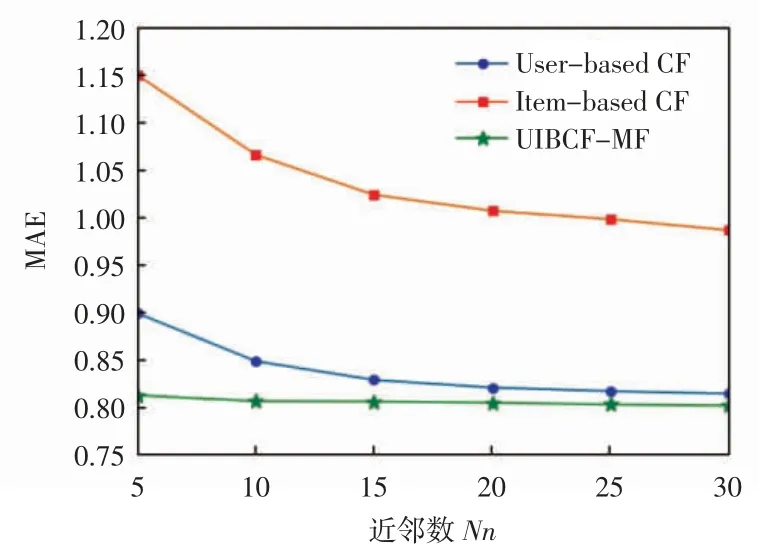
图 2 user-based CF、item-based 与 UIBCF-MF 的MAE 比较

由图1、图2 可知，当近邻数逐渐增大到接近30时，user-based CF、item-based CF 的 RMSE、MAE 值均趋于稳定，而UIBCF-MF 算法受近邻数影响较小，RMSE、MAE 值随着近邻数增大稳定减小，相较单一user-based CF、item-based CF 算法，在利用近邻用户或物品进行评分预测的同时，考虑到近邻用户或物品较少时会造成推荐不准确，故适当降低该算法比重，提高其他2 种算法权重因子，结果表明UIBCF-MF 算法始终获得较好的推荐结果。

第2 组实验为固定user-based CF、item-based CF算法所得预测矩阵，当隐藏矩阵因子不同时，传统单一的MF 算法与本文提出的UIBCF-MF 算法的实验结果对比，MF 与 UIBCF-MF 的 RMSE 与 MAE 比较如图3 所示。

由图3 可知，隐藏矩阵因子逐渐增大时，MF 所得推荐误差RMSE、MAE 均增大，而UIBCF-MF 算法受隐藏矩阵因子影响较小，RMSE、MAE 值随着隐藏矩阵因子增大稳定增大，值为2 时，误差最小。单一的MF算法解释性不强，故考虑物品和用户喜好信息，使得预测评分更加合理准确，结果表明UIBCF-MF 算法始终获得较好的推荐结果。

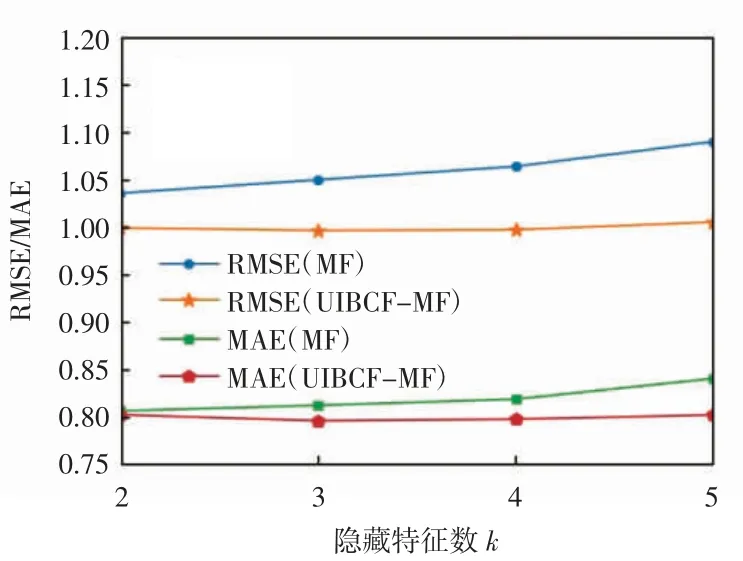
图 3 MF 与 UIBCF-MF 的 RMSE 与 MAE 比较

第3 组实验为固定user-based CF 算法所得预测矩阵，当近邻数不同时，文献[8]中IACF 算法在隐藏因子不同时与本文提出的UIBCF-MF 算法的实验结果对比，IACF 与 UIBCF-MF 的 RMSE 比较如图 4 所示，IACF 与 UIBCF-MF 的 MAE 比较如图 5 所示。

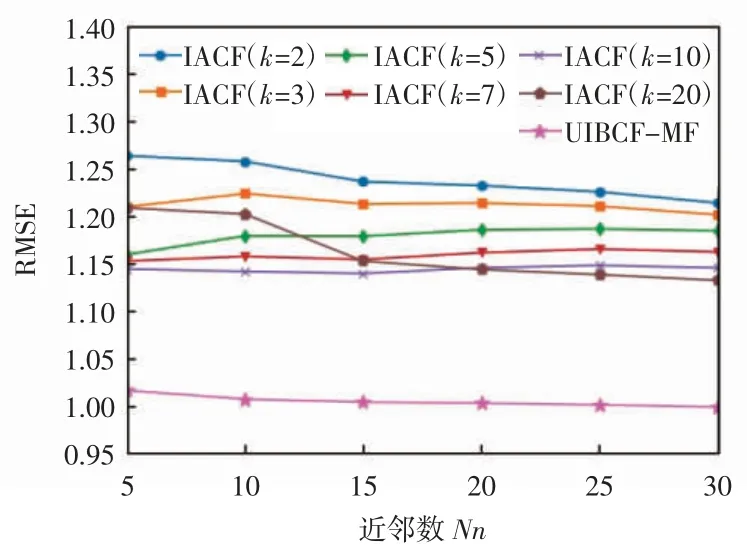
图 4 IACF 与 UIBCF-MF 的 RMSE 比较

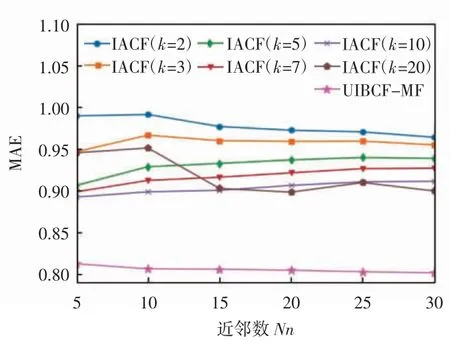
图 5 IACF 与 UIBCF-MF 的 MAE 比较

由图4、图5 可知，随着近邻数增大，文献[8]中IACF 算法RMSE、MAE 值变化较小，本文提出的UIBCF-MF 算法RMSE、MAE 值稳定减小，在隐藏因子不同的情况下，本文提出的UIBCF-MF 算法在item-based CF、MF 算法的基础上考虑基于用户的信息，采用匹配度进行度量动态调整权重，对每1 个评分值都考虑到了其用户和物品特性，并进行权值调整，结果表明UIBCF-MF 算法误差值远小于IACF 算法，始终获得较好的推荐结果。

5 结 语

本文提出了一种基于信息匹配度的混合推荐算法，采用新的评分规范化方法进行评分预测，使得评分数据更为规范，近邻影响更加合理，结合基于用户协同过滤、基于物品协同过滤和矩阵分解推荐方法各自的优点，得出某一用户-物品的预测评分，根据3 种算法与历史信息匹配度进行动态加权混合求得，不仅数据集稀疏问题得到了解决，也使得推荐结果更加准确并具有可解释性，使用Grouplens 提供的MovieLens数据集进行实验，结果表明，相较于传统的推荐方法，该算法推荐误差更低，适应性更强，稀疏矩阵中也能取得较好的推荐结果，冷启动问题得以解决。