改进Dijkstra 机器人路径规划算法研究

陈智康 ，刘 佳 ，2，王丹丹 ，张运喜 ，2

（1.天津职业技术师范大学天津市信息传感与智能控制重点实验室，天津 300222；2.天津职业技术师范大学自动化与电气工程学院，天津 300222；3.青岛市技师学院，青岛 266229）

自从1959 年恩格尔伯格发明了第一台机器人并用于生产之后，机器人这一新事物就逐渐成为科研人员研究的焦点。随着科学技术以及新兴技术在人工智能领域不断发展，机器人的相关开发成为其中的一个小分支。多类型的机器人出现在科学行业中，如类人机器人、移动机器人、水下机器人等。目前相关领域研究者的研究集于陆地移动机器人方面，该研究被细分为3 个方面：构建地图的机器人环境、路径规划以及机器人寻路导航。20 世纪60 年代末，斯坦福研究院研制了自主移动机器人，提出了路径规划问题是移动机器人的关键问题。移动机器人路径规划是指根据某种优化标准（劳作代价小、路径最少、耗时最短），在机器人的工作空间中探求一条从起始位置到目的位置的无碰撞最优，也可能是次优路径[1-2]。现今路径规划算法主要分为传统路径规划算法和智能路径规划算法2 大类。He 等[3]针对路径规划问题，提出了栅格法用于解决机器人路径规划问题，此方法对机器人的运行环境进行了栅格表示，简化了规划工作。Sariff 等[4]针对未知环境的路径规划问题，提出了人工势场法用于移动机器人路径规划，虽然收敛速度快，但存在死锁现象。马丽莎[5]提出了一种用矩形表示不规则障碍物的可视图法，简化了路径规划中构建环境地图的工作。文献[6]提出将路径规划中的路段描述成一系列中途点，能够根据规划要求完成解空间的搜索，输出最优个体，但是存在算法编码较长的问题，导致收敛速度慢，计算量大。Ammar 等[7]针对移动机器人在已知环境中的路径规划问题，提出了一种松弛Dijkstra 算法，但是其结果中存在多余的路径折损，有时出现较大误差。经典的Dijkstra 算法使用在机器人自主构思路径中所产生的路径，存在少许冗杂的点，在很多情况下整个运算过程运算次数过多且容易陷入局部最优解，所以导致整个寻路过程会走很多弯路。因此，为了将Dijkstra 算法能够应用于机器人路径规划且获得较好的规划效果，对Dijkstra 算法进行改进十分必要。本文将蚁群算法中信息素的计算方法引入原Dijkstra 算法中，完成算法优化。

1 经典Dijkstra 算法

1.1 可视图建模

可视图地图是构建移动机器人环境地图的一种方法，这种算法将环境中的障碍物抽象为几何图形，可以理解为图中所看到的是事物的俯视图，在平面上能够反映障碍物所占的面积。在路径规划领域，考虑求解方便，可把移动的任何机器人抽象成一个点，暂时计算这些障碍物的大小，这时障碍物等效成一个任意形状的图形。后期分别把地图中的出发点、障碍物以及所要到达目的地通过线段或是曲线连接起来，每条连接线不能从障碍物上面穿过且不能和边界有接触，这样得到一张环境地图，这张图被称为可视图。该可视图中所有的线段端点是可见的，从起始点到目标点可以通过线段到达。利用可视图建立机器人路径规划的环境地图和建立的栅格图相比，可视图建立的环境地图更接近于真实的环境实景。栅格图的优点是能够在环境中放置很多障碍物，增加机器人路径规划的难度，用来检验算法的抗干扰能力，但栅格图在很多情况下不能表达复杂的障碍物信息。可视图的原理比较简单，且比较容易实现，在大部分应用场景中，涉及静态的全局路径规划一般会使用可视图进行环境建模[8]。

虽然可视图比较好实现，如果障碍物增加得很多并达到一定程度的话，或者说是在障碍物外形轮廓十分复杂时，在可视图中会出现很多的连线，这就增大了算法的工作量，影响真正的路径规划结果[9]。构建复杂的环境地图时，先不要使用可视图法，可以在简化环境地图形状后再进行路径规划，这样就能够节省很多规划上所耗费的不必要的计算。环境可视图如图1所示。

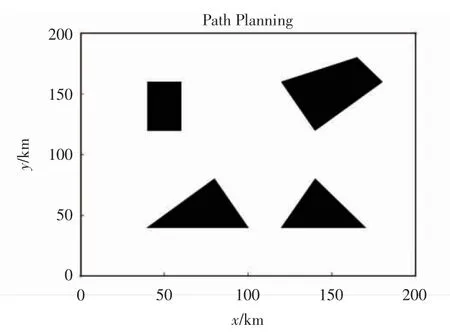
图1 环境可视图

1.2 传统Dijkstra算法步骤

Dijkstra 算法是一种经典的求解最短路径的算法，用于计算一个节点去往其他各个不相关节点的最小移动代价[10]。本思想是把在图中无论如何出现的所有节点分离为2 组，第1 组包含被准确认定是最短路径的节点，第2 组存放待检查的不确定的节点。根据最小移动代价逐渐增大的顺序，逐个将第2 组需要检查的节点加入到第1 组中，一直到从起始点出发可以到达的所有节点都包含在第1 组中。Dijkstra 算法运行的主要特征是以机器人抽象的出发点为中心向外层层延伸，直到延伸到整个区域的末端为止。Dijkstra 算法一般能够在最终得到最优的路径，但是这个路径偶尔会出现冗余拐点，由于其遍历节点多，所以有时算法的效率不高[11]。Dijkstra 算法流程如图2 所示。

分别创建 2 个表，为：START 与 FINISH。START表中存放环境中已经生成存在但是未经计算的节点，FINISH 表中存放所有经过计算考察的节点。

（1）观测寻找在环境路网中离起始源点近而且是没有被计算过的点，把满足调节的点放在START 数组中等待检查。

（2）从START 表中找出距离起始点最小的点，然后把该点放进FINISH 表中。

（3）遍历去寻找考察当前此点的子节点，计算出起始源点到这些子节点的距离值，将值存入数组中用来排序，将子节点放在START 表中。

（4）重复（2）和（3），直到把 START 表中的点全部清空，或者找到真正要去的目标点。

1.3 Dijkstra算法的思想

（1）将环境可视图中出现的节点或是顶点分别加入2 个组，其中一组存放经过求解验证为最短路径所经过的顶点，该集合用FINISH 表示，刚开始时START表中只有1 个起始点，在后面的运算过程中每得到1条最短路径，就把相关节点加入到集合FINISH 中。如果全部的顶点都加入到FINISH 后，此算法运算完成。另一组存放未经过考察且还未被认定为最短路径的顶点，用START 表示。

（2）在将顶点逐渐加入到FINISH 表的过程中，在运行算法期间总保持从出发点到FINISH 表中各个点的最短路径的长度不超过出发点到START 表中任何顶点的最短路径长度。

典型的Dijkstra 算法在寻找最优路径的准则上较为单一，以某一个点为中心向外层层扩展就类似于画圆，随着搜索半径的逐渐增大，最后总能找到想要的目标点，但同时最优路径会出现一些无关的冗余点，这样在一定程度上给实际的移动机器人造成寻找路径的困难[12]。如果能够对经典算法的计算准则进行优化，达到减少路径中拐点的目的，就可以减少一大部分机器人寻路所耗费的时间。在大面积环境中使用Dijkstra 算法时，由于每次都要从START 列表中挑选离原始点最近的点，这样导致规划效率不高，在排序过程消耗很多不必要的工作时间[13-14]。

2 改进Dijkstra 算法

在经典的Dijkstra 算法中，用来判断最优路径点的方法就是从源点找到最短欧式距离的点，作为合适的最短路径所经过的点，这样所找出的路径往往会有一些冗余的点。优化就是在寻找节点的过程中做仔细筛选，遵循原经典算法寻优准则有时会陷入局部最优，本文所做的改进是在原Dijkstra 算法的基础上，增加了一部分寻优准则函数，在原本判断为最优路径点之中利用相关路径的信息素或是密集程度做排除，在确定放入FINISH 表中之前做好删减，这样在最后就可以从终点到起点再回溯到起点。

2.1 环境地图构建

在真实平面环境中，建立用于机器人路径规划的环境地图模型一般有2 种选择：栅格法和可视图法。栅格法就是将障碍物模拟成小方格的集合，相当于将场景的所有事物进行二值化替代，障碍物为1，非障碍物为0。可视图法就是将环境中的障碍物抽象成俯视图，连接起点和障碍物各个顶点，再加上和周围边界的连接生成带链接线的环境地图，这样做出地图之后能够为运行寻路算法减少很多工作量。带链接线可视图如图3 所示。从图3 中可以看出，机器人所走的无碰撞最优路径需要依靠算法实现[15]。

图3 带链接线可视图

2.2 Dijkstra算法改进步骤

经典的Dijkstra 算法得到的路径存在冗余杂点，本文所做的工作就是减少在原最短路径上存在的冗余杂点[16-18]。在原来算法基础上加上类似于蚁群算法中的信息素概念的判别因子，相关步骤加入了带信息素因子的算式并进行判别，为原先的算法添加了一些计算公式。

2.2.1 信息素因子

本文所添加的信息素因子类似于蚁群算法中的信息素浓度。蚁群算法是由Dorigo M 等在20 世纪90年代构思出的一种属于生物启发式智能优化算法，它来自人们对蚂蚁寻找路径方法的研究[19]。人们在观测蚂蚁搜索食物时候发现，蚂蚁在寻找食物时，总在路过的道路上留下一种被叫做信息素的生物性物质，信息素可以在原来的地点保留一段时间，使得在附近区域内的其他蚂蚁能够发现该信息素的存留，后面过来的蚂蚁在选择要走的路时，会挑选信息素比较大的路径，每个蚂蚁经过路径都会留下自身的信息素，随着信息素不断增强，之后最优的路径就会逐渐显现出来[20]。信息素寻路示意图如图4 所示。

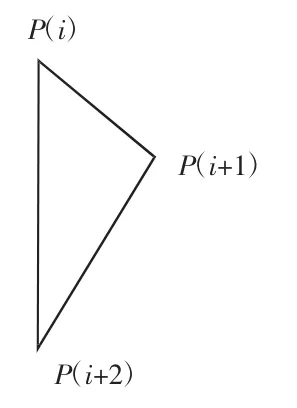
图4 信息素寻路示意图

假设机器人从 P（i）到 P（i+2），P（i）、P（i+1）、P（i+2）3 个点是经过经典Dijkstra 算法运算得到的3个机器人经过的最短路径点。这3 个点会被放在FINISH 表中，算法的运行结果会认为经过这3 个点是最优的路径。但显然直接从 P（i）到 P（i+2）比先从 P（i）到P（i+1）再到P（i+2）机器人行走的移动代价要小很多，也就是说从 P（i）到 P（i+2）留下的信息素会比较多。本文所做的改进是添加了信息因子作为判断准则，用来做进一步筛选。

信息素因子计算公式为

式中：（xs，ys）为起始点坐标；（xt，yt）为终点坐标；（xi，yi）为路径中第i 个节点；cmn为信息素因子。

信息素因子计算公式的分子是点与点之间移动欧式距离的叠加，其分母是起点到终点的曼哈顿距离的叠加。该因子越小说明经过这几个节点的路径越接近最优路径。信息素因子运用示意图如图5 所示。

在图5 中运用上述公式计算，假若从P（i）到P′（i+1）再到P（i+2）计算出信息素因子为C1，从P（i）到 P（i+1）再到 P（i+2）计算出的信息素因子为C2。如果C1＜C2，那么C2 所代表的路径除了和C1 所代表路径的共有的点外，其他的点被删除，不再存放在FINISH 表中。通过这种方法将经典Dijkstra 算法得到的路径点中冗余的点删除，剩下的点便可存放在FINISH 表中。

2.2.2 改进Dijkstra算法设计

在上述经典Dijkstra 算法步骤3 中，如果得到的新节点数≥2，先不放入FINISH 表中，计算经过这些节点且有相同移动效果路径的信息素因子的值，将信息素因子较大的值所代表的路径上的节点（除了共有节点外）删除后，剩下的节点再加入FINISH 表中。在对新节点进行排序之后，不断运用这种准则进行判断，直到完成对所有节点的遍历。最后得到的FINISH表中，从终点依次按照节点序号递减到到达起点就得到一条最短路径。在原始的Dijkstra 算法中，每次得到2 个以上新节点时，运用信息素因子判断准则，判断这些新得到的最短路径节点是否可以存到FINISH 表中。这样在FINISH 表中存放的节点可以减少很大一部分冗余[21-22]。

蚁群算法本身就是一种在图中寻找优化路径的概率性算法。其求解模式可以将问题求解的快速性、全局优化特征以及有限时间内答案的合理性相结合。正反馈式的信息传递和积累保证了蚁群算法寻优的快速性。而算法的早熟性收敛又能够通过其分布式的计算来避免。同时，具有贪婪启发式搜索特征的蚁群系统又能在搜索过程中尽早找到可以接受的解去解决相应问题。本文的信息素因子来源于蚁群算法，通过将其加入经典Dijkstra 算法，对Dijkstra 算法中的路径节点进行寻优，加快了算法的运算速度。经过改进后的算法能够根据解的分布情况自适应地进行信息素更新，从而动态地调整了各路径上的信息素强度，增加了解空间的多样性，增加了在全局规划上的搜索能力，有效规避了局部收敛和早熟现象。因此，通过使用蚁群算法优化经典Dijkstra 算法，能够获得较好的规划效果，方法切实可行。

3 实验结果

本文改进的Dijkstra 算法采用可视图法构建地图，将得到的新节点在加入到FINISH 表之前进行筛选，对模拟可视图的带有障碍物机器人的运行环境进行路径规划，得到最优路径点的同时也增加了寻路的速度。

3.1 程序设计

为验证本文算法改进的有效性，在Windows 7 系统下的Matlab 2014a 开发平台上，通过Matlab 程序脚本首先实现传统Dijkstra 路径规划算法，然后再实现改进后的算法，最后将实际运行后的2 个效果图进行对比。程序设计流程图如图6 所示。

图6 程序设计流程图

3.2 结果分析

在程序设计中，对经典Dijkstra 算法、改进后的Dijkstra 算法进行运行测试，并将得到的运行结果进行对比分析。算法仿真程序运行环境为windows 7 的64位操作系统，处理器为IntelCorei5CPU、16G 运行内存，算法仿真运行结果如图7 所示。

在图7 中，断续实心点轨迹代表经典Dijkstra 算法路径规划的运行结果，虚线轨迹代表改进后Dijkstra算法运行结果。在原始算法规划的轨迹中存在一些多余的拐点，在添加信息素因子判断准则优化后的算法，生成的轨迹比之前的轨迹少了一些多余的拐点。运算次数如图8 所示。

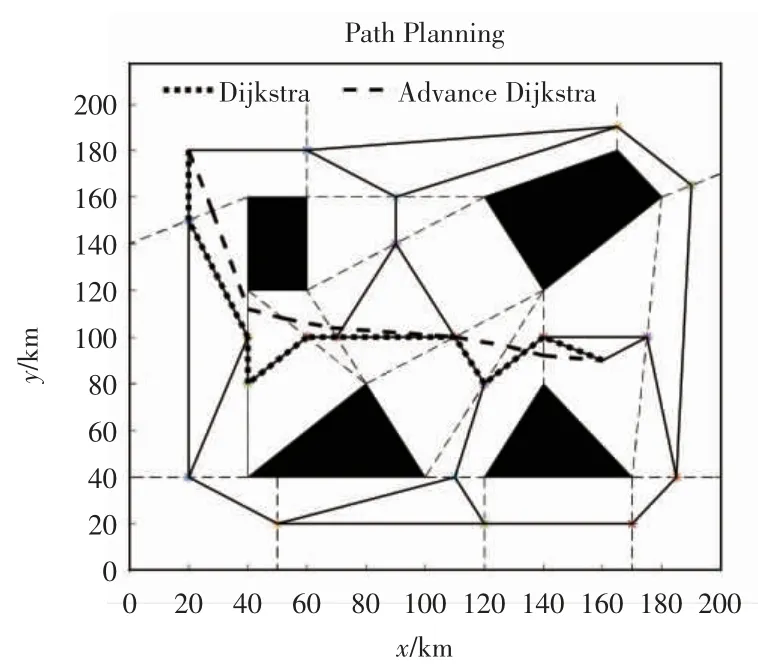
图7 仿真运行结果

图8 运算次数

从图8 可知，在110 左右的运算次数之后便基本上完成路径规划的任务，迭代次数少。在运行效率上，改进后的Dijkstra 算法能够实现更加快速地搜索，在一定程度上减少了搜索时间。

4 结 语

本文针对陆地移动机器人路径规划问题，提出了一种改进Dijkstra 算法，该算法能够在可视图地图上实现平面路径规划，将蚁群算法中信息素因子加入原Dijkstra 算法的寻优准则中，在一定程度上避免路径规划中出现冗余点，提高机器人路径规划效率。仿真结果表明，经过改进的Dijkstra 算法能够更高效地完成路径规划任务。如果将此算法运用到现实中的机器人路径规划，能够在一定程度上使机器人所走的路径尽可能平滑。在引入了改进Dijkstra 算法后，使陆地移动机器人在获得周边环境信息进行地图建模后能够顺利找到适合移动的最佳路径。改进算法对于家庭、军事、医疗等服务型机器人路径规划的研究具有一定的现实意义。