葡萄酒消费者偏好度调查研究

郭梦笛，赵小山

（天津职业技术师范大学理学院，天津300222）

“回归”统计方法最初由英国生物学家、统计学家高尔顿提出，经过一段时间的发展，出现了最小二乘回归、分位数回归、定序回归等一系列回归方法。其中，定序回归模型从提出到现在也经过了一定时期的发展。陈素敬[1]采用均值比较、相关分析与定序Logit回归的方法探讨了残疾人福利三角与主观幸福感存在群类型分化；王晨[2]采用单因素影响分析、定序回归方法对二手车保值率进行分析；杨蕊岚[3]运用因子分析和定序回归模型对云端用户行为可信性进行了评估，进一步确保云端平台的安全；缪宇环[4]采用非参数检验与定序回归对我国过度教育现状及其影响因素进行了分析，发现学历、公司规模等对教育过度现象有着显著影响；王存同等[5]运用Tobit 模型与定序回归探究了退休是导致个体健康水平降低的重要因素；姚萱等[6]运用多因素logistic 回归分析探究了社会人口、健康状况、知晓情况是居民社区服务利用的重要影响因素；杨威等[7]运用回归分析方法为在体育社会学中的应用提供方法指导。目前，在国际上Sader 等[8]提出以排名的形式合并相关的评价可以增强定序回归模型的有效性；Zhu 等[9]提出了合成少数类过采样技术处理非平衡定序回归问题，该方法在平均绝对误差方面优于典型的过采样算法；Wu 等[10]得到了不同的影响煤炭事故发生的因素会产生不同程度的煤炭事故，而管理因素导致更高水平的煤炭事故的结论；Juliana 等[11]通过定序回归模型发现在相同实验条件下，不同菌株的生物膜阶段存在差异，序列回归模型可以用于预测肠道链球菌生物膜阶段与温度等因素相互作用的关系。汪宏玲[12]运用方差分析、logistic 定序回归研究了年龄等因素对消费者口感偏好的影响，可在获取了消费者年龄等信息的条件下预测消费者的口感偏好。在进行消费者意愿的研究过程中，左妹华等[13]通过建立logistic 预测模型，发现将属性与具体产品进行匹配并推荐给消费者可扩大在线平台的购买转化率；胡琴心[14]利用K-means 聚类方法和logistic 回归发现离退休人员的生态消费水平最高。本文采用消费者对于某一种类型的葡萄酒的打分累计得分来判断消费者的偏好度，运用赤池信息量准则（AIC 信息准则）对数据进行定序化处理，采用统计学中的经典回归模型——定序回归模型对实际案例进行分析，研究消费者喜好程度的主要影响因素，得出相应的结论，从而可以引导实际的商品销售过程。

1 商品的数据特征

在进行研究时，选取的数据一般有2 种：实际的交易过程中产生的数据和实验数据。在交易过程中，为了解消费者满意度，通常根据一线客服人员的直接询问和经验来进行判断，在一线客服人员进行询问时，会发现这种方式消耗大量的时间成本和精力，市场的庞大、数据的复杂性、各种环境之间的干扰因素使研究难以开展，所以研究人员研究出了另一种方式来控制变量的干扰因素，即实验数据。实验数据就是在一定的环境下控制其他的变量因素，只研究所需要的因变量指标的一种数据。实验数据发现与因变量相关的关系一般是因果关系，在实验数据的收集过程中存在不足，那就是有时实验数据的获取是高度简化的过程，控制了无关变量的影响，但有时却与实际环境相去甚远。在数据的选取过程中，运用八爪鱼数据收集器在京东官网上收集数据，选取200 个关于葡萄酒类型的数据。在浏览数据时发现数据当中有许多缺失数据，其中葡萄酒口味的缺失数据45 个，葡萄酒容量的缺失数据40 个，进出口的缺失数据26 个，葡萄酒类别的缺失数据32 个，葡萄酒包装的缺失数据32 个，所以样本中平均缺失数据35 个，因此删除35 个缺失多的数据，得到了本文所需的165 个数据。由于数据有缺失，需要填补缺失数据。填补缺失数据的方法为在网页上查询葡萄酒的类型，再填上所需填补的内容。

在数据的收集过程中，为了了解消费者是否满意商家生产出的商品，从而促使企业生产出更能让消费者满意的商品，在这里让消费者对商品的满意程度进行打分，对于一般的线性模型来说，需要消费者对产品的偏好度打出一个连贯的得分，最好得分的分布应是正态分布。但这在实际操作过程中是不可实现的，在实际操作过程中，如果对消费者的调查是复杂的，那么长时间的询问会让消费者失去配合的兴趣，从而导致调查数据的失真。所以在这里采用消费者对于某一种类型的葡萄酒的累计得分来进行判断。在观察消费者的累计打分时，由于分数的复杂性和多变性，不易看出消费者对哪一种类的葡萄酒偏好比较多，所以本文把累计得分划分为5 个区间，相应地对应喜欢的5 个等级，分别为：无所谓、一般喜欢、比较喜欢、十分喜欢、最喜欢。而由于葡萄酒的种类特别多，在这里进行研究时可以把葡萄酒分为3 大类，分别为：红葡萄酒、白葡萄酒和其他类型的葡萄酒。

在逻辑回归中，所要求的指标取值也是只有2 个可能，不适用于目前所要研究的数据，所以需要一种专门的模型。而定序回归分析是解决消费者偏好度这一实际问题的常用方法。在使用定序回归模型时，常用的因变量的取值已经不适用，这时需要一种特殊的、专门为定序模型所设置的因变量的取值，即定序指标。

在进行定序回归分析前首先要对搜集的数据进行定序处理。定序尺度常用几个自然数表示数据的等级，虽然定序数据仅仅代表不同的等级，不能表现出各个等级与等级间的“空间距离”，但是通过进行定序数据的处理，可以把离散的随机数据转化为定序的潜变量数据。在本文中采集的影响消费者偏好度的因素有葡萄酒的类别、价格、商品毛重、商品容量、进出口、口味与包装这 7 个因素，分别定义为 X1、X2、X3、X4、X5、X6、X7。通过观察这些因素可以有以下的划分：由于红葡萄酒与白葡萄酒的数量多，其他种类的葡萄酒数目少，所以定义红葡萄酒为0，白葡萄酒为1，其他为2；在进出口类型中划分为进口葡萄酒与国产葡萄酒，定义进口为0，国产为1；将商品毛重分为4 个区域：0~3 kg 为1，3~6 kg 为 2，6~9 kg 为 3，9 kg 以上为 4；葡萄酒的价格定义为：0~150 元为 1，150~300 元为 2，300~450 元为 3，450~600 元为 4，600 元以上为 5；葡萄酒的容量定义为：750 mL 为1，其他为0；葡萄酒的口味定义为：半干型为1，半甜型为2，干型为3，甜型为4，其他为5；葡萄酒的包装定义为：瓶装为1，礼盒装为2，箱装为3，其他为4。在挑取自变量时运用AIC 信息准则对自变量进行分析与选择。

在进行变量选择时，首先对数据进行多元线性回归分析。通过R 程序对数据进行分析，可得到回归方程的系数没有通过显著性检验。接下来用逐步回归的方法进行变量的选择。在逐步回归过程中，运用AIC信息准则，当 X1、X2、X3、X4、X5、X6、X7作为回归方程的系数时，AIC 的值为170.66。去掉X6时回归方程的AIC 为167.68，去掉X7时回归方程的AIC 为167.71。由于去掉X6使得AIC 达到最小，而且去掉X6之后AIC 的值均增加，逐步回归分析终止，得到最优的回归方程。去掉X6进行回归分析，发现回归系数的显著性水平有所提高，X3、X7的显著性水平仍然不理想，再进行逐步回归分析优化。去掉X7后AIC 的值从167.68增加到了167.82，是所有变量中AIC 的值增加最少的。去掉X7进行多元分析发现所有的检验均为显著。由此自变量选取了 X1、X2、X3、X4、X5。

本文消费者的累计评价得分可以用喜欢程度的等级来进行表示，将喜欢程度等级划分为5 个等级，第1 等级为无所谓，用1 表示；第2 等级为一般喜欢，用2 表示；第3 等级为比较喜欢，用3 表示；第4 等级为十分喜欢，用 4 表示；第 5 等级为最喜欢，用 5表示。这里表示的消费者喜欢程度的等级为所需的因变量。在数据选择完毕后，需标准化处理数据，并进行简单的分析整理。评价指标对消费者偏好度的影响如表1 所示。

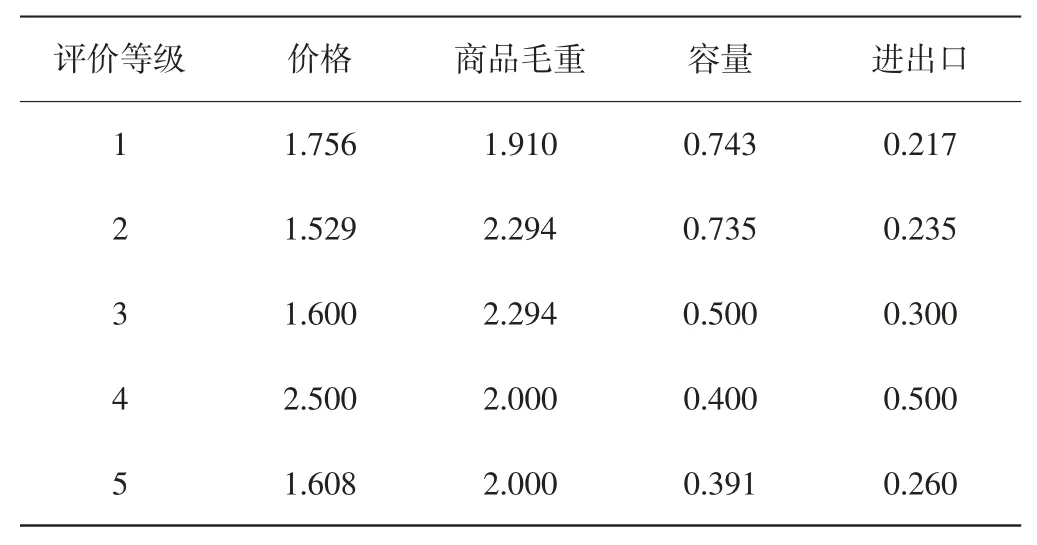
表1 评价指标对消费者偏好度的影响

在每个评价等级的类别上对每个影响因素的均值进行分析。由表1 可以看出，随着评价等级的增加，也就是随着人们对商品喜好程度的增加，每种影响因素的均值都稳定在一定范围之内。对于商品容量这一影响因素来说，随着喜好程度的增加，商品的容量逐步减小，这一现象估计是在现实商品销售过程中，商人为了增加利润，对消费者满意的商品进行饥饿营销；在进出口的均值中可以看出“十分喜欢”的进出口的均值最大，在价格的均值中也可看出对于“十分喜欢”等级的商品的价格最高，这一现象从侧面反映出了价格也是影响喜欢程度的重要因素。

2 模型介绍

定序数据的回归分析模型多采用多特质多方法模型，这种模型多运用于心理学研究。然而这种方法在运用时只考虑了个体判断阈值的等级之间的差别，在运用过程中忽略了不同个体之间的动机。因此，本文采用一种能够分析定量数据的统计模型——定序回归模型。

在数据分析时，首先要进行模型的选取。为此选取一般的定序因变量回归模型[15]。解释变量X =（1，X11，X12，X13，X2，…，X5）′，对应的的回归系数为 β =（β0，β11，β12，β13，β2，…，β5）′，其中 β0是截距项。然后再定义：X′β=β0+β11X11+β12X12+β13X13+β2X2+…+β5X5。同0-1 逻辑回归一样，直接定义Y=X′β+ε 是不适用的，因为X′β+ε 为任意取值的数值，而Y 为离散型的定性的指标，因变量Y 为消费者对于商品的偏好程度，而在消费者对产品进行打分时，内心会有一个更加精确的产品的偏好，该偏好在进行偏好度调查时没有被直观显示，是潜在的一种喜好程度，而且这种喜好是连续的。消费者对于不同类型的相近产品喜好度是相近的，当消费者进行产品的选择购买时就会出现左右为难的情况。最后假设用M 来表示消费者潜在的偏好，可以由分数显示出来。当消费者对某一产品更加喜欢时，累计得分就会越高。对应地，当M 取值特别低时，消费者对某一产品的偏好度就会低。在数学上，可以假设

式中：c1-c4为4 个喜好程度划分的的阈值，需要根据数据进行分析，然后预测评估，c1= 1 500；c2=3 000；c3=4 500；c4=6 000。

若潜在变量M 为连续变量，则假设M 为一个普通的线性模型：M=X′β+ε。假设ε 服从一个均值为0，方差为1 的标准正态分布，方差为σ 时，则重新定义一个新的残差得到回归系数为潜在变量为因此 var=1 则回归系数 β 是不成立的。因此选取方差为1 的模型进行求解。

假设 ε~N（0，1），能够得出的各个取值 Y 的条件概率。假如Y = 2 时

P（Y = 2|X）= P（c1≤M ＜ c2）= P（c1-X′β≤ε ＜c2-X′β）= Φ（c2-X′β）- Φ（c1-X′β）；

假如Y = 3 时

P（Y = 3|X）= P（c2≤M ＜ c3）= P（c2-X′β≤ε ＜c3-X′β）= Φ（c3-X′β）- Φ（c2-X′β），……，能够得到Y 的条件概率如下

其中Φ（t）代表的是一个标准正态分布的分布函数，式（2）即为 PROBIT 回归模型。

同0-1 变量逻辑回归与普通的线性回归类似，对于PROBIT 回归模型来说研究的是回归系数β。对于一个给定的解释变量Xj，βj=0，在给定其余解释变量的条件下，该指标对于解释条件概率pk（X′β）没有影响，因此对于解释变量条件概率pk（X′β）没有帮助，对于解释定序变量Y 也就没有任何帮助。若βj＞0，在给定其余解释变量数值恒定时，指标Xj的上升就会带来条件概率的下降，也就是说，因为Y 值取值偏小的可能性小，Y 的取值有可能变得更大。从一方面看，Y 的取值与指标是“正相关”的关系。若βj＜0，在给定其他解释变量不变的情况下，指标Xj的增加会带来解释变量条件概率pk（X′β）的增加。因而Y 取值偏小的可能性升高，也就是说Y 的取值有可能变得更小。从另一方面看，Y 的取值与指标是“负相关”的关系。

用（Yj，Xj）代表第j 个个体的数据，其中Yj是因变量，Xj=（Xj1，Xj2，…，Xjp）′是对应的解释变量，那么 Yj与Xj的联合似然函数为β，c）}I(Yj=k)，c=（c1，c2，c3，c4）′，对公式做对数变换后，得到对数似然函数为极大化对数似然函数得到极大似然估计，为该估计量是相合一致的无偏估计，而且该估计是极限正态。为每个系数的估计差做判断，计算与系数相对应的 p-值，假设检验 H0：βj=0，H1：βj≠0。

单独检验多水平因素，对比以下模型。

模型 1 X′β=β0+β11X11+β12X12+β13X13+β2X2+… +β5X5

模型 2 X′β=β0+β2X2+… +β5X5

把模型1 与模型2 的离差分别记作DEV1、DEV2。模型1 比模型2 灵活，因此DEV1＜DEV2。若原假设= 0 为真，DEV2-DEV1的值不会特别大。在样本量足够大的情况下，服从自由度为df=3 的卡方分布。因此可近似计算出模型全局检验的p-值，并以此为依据，对葡萄酒品牌这个因素的显著性有所判断。

评价指标的极大似然估计如表2 所示。在表2中，商品毛重、白葡萄酒和其他类别的葡萄酒的参数估计为正，高度显著，白葡萄酒的极大似然估计最大，说明白葡萄酒在葡萄酒消费市场中所占的比例最高，具有明显的产品优势；5 个解释变量的标准误差均在0～0.3，其中价格的标准误差最小，这也说明价格的数据分析更贴合实际。T 统计量在-4～4 之间取值；葡萄酒类别、价格、容量、进出口、商品毛重的p-value 均小于 0.05，所以拒绝原假设，因此 X1、X2、价格、容量、进出口、商品毛重均对消费者对于葡萄酒偏好度的影响是显著的。价格（X2）是最重要的，因为它对应的极大似然估计最大（0.6），这说明了价格对于消费者的重要性。

表2 评价指标的极大似然估计

3 预测评估

Yi为消费者的未知偏好，Xi为某一葡萄酒的各种属性，分析数据建立定序回归模型，计算得到极大似然估计将此估计用于未来数据，对其因变量的各种取值的概率估计为

此概率量化了消费者各种偏好的可能，若偏好程度k 可能性越大，预测= k。由此定义预测=把消费者偏好概率预测pk为最大，定序变量只有 2 个取值的条件下，定义极小化判断错误概率

考虑加权错误判断概率WMCR，对稀有样本给予更大权重，丰富样本给予更小权重，定义WMCR =以加权错误判断概率为标准，产生的预测为

极小化MCR 的预测结果如表3所示。

表3 极小化MCR 的预测结果

表3 中，完全准确的预测样本量为80；总预测样本为165；相应的整体错误判断率MCR =（165-80）/165=0.52。

4 结 语

定量数据在指标评价体系中比较常见，在消费者模型中通常建立定序回归模型，并对解释变量及响应变量作出解释，对消费者偏好度作出预测。本文研究了葡萄酒的类别、价格、容量、商品毛重、进出口对于葡萄酒消费者偏好度的影响程度，可以看出价格与喜好程度有很大的关联，商品的价格很大程度上影响了消费者的喜好。消费者更倾向于价格在450～600 元之间的葡萄酒。由于数据来源于京东商城，消费者群体年龄、性别等影响消费者购买力的数据对于本文来说是未知的，而且消费者的偏好度与消费者的购买水平无法等同，接下来的工作会更详细地考虑评价指标，如年龄、性别以及消费者对葡萄酒的了解程度等。因此，完善理论研究进而进行实际意义的指导是下一步研究的重点。