次序L1 惩罚估计在高维数据分析中的应用

郭依菏，訾雪旻

（天津职业技术师范大学理学院，天津300222）

随着生物信息学、生物医学、计量经济学和机器学习等领域的迅猛发展，高维数据在实际应用中越来越受到关注。为了能够全面地分析数据，研究者总是尽可能地收集与研究问题相关的变量。如医学研究人员在研究哪些基因变异会导致某种病变时，需要同时追踪成千上万的基因序列的表达。但是基于检测成本等客观因素，研究人员往往只能得到很小的样本量。对于变量的数量远远大于观测值的数量这种情况，寻找合适的变量选择方法，提高变量筛选的效率及正确率，成为近年来统计学界的热点问题之一。Foster 等[1]提出风险膨胀准则（risk inflation criterion，RIC），使用L0范数作为惩罚项，但对于高维情况，此方法通常会导致模型中包含很多不相关的变量，特别是在稀疏情况下，预测能力表现相当差。Tibshirani[2]提出套索算法（least absolute shrinkage and selection operator，LASSO），其通过使用L1范数作为惩罚项，克服了传统方法在变量选择上的不足，成为较流行的处理高维模型中变量选择的方法。Bogdan 等[3]受 Benjamini-Hochberg 多重检验校正方法的启发，在LASSO 方法的基础上，提出了一种新的变量选择方法——次序L1惩罚估计（Sorted L1Penalized Estimation，SLOPE）方法[4]。本文利用数值模拟方法分析比较了SLOPE 和LASSO 方法，结果表明SLOPE 方法对一般稀疏回归模型有很好的筛选效果，同时利用实证分析研究了SLOPE 方法的有效性。

1 次序L1 惩罚估计算法

设n 维响应向量y 是由一个简单的线性模型生成的

式中：Xn×p为设计阵；β 为 p 维向量回归系数；Z 为 n×1的随机误差项。

首先考虑在正交设计下，令X′X=Ip，且随机误差项Z 独立同分布于正态分布即N（0，σ2In）。此时不需考虑交互效应，定义˜为响应变量y 和设计阵X 的乘积，则回归模型可以改写为

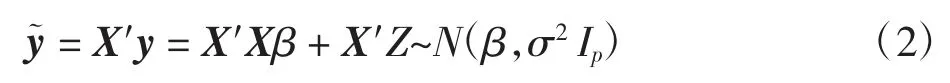
为了控制错误发现率水平在q∈[0，1]，首先采用BH方法对响应变量以降序排序，即令与之对应的假设检验分别为 H(1)，…，H(p)，定义参数iBH如下

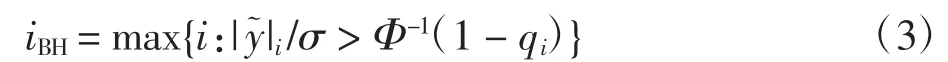
当i≤iBH时，拒绝原假设H(i)。集合i 为空时，定义iBH=0。与传统的Bonferroni 校正方法相比，BH 方法是一种自适应过程，因为拒绝的阈值iBH由数据直接驱动。SLOPE 方法选取λBH（i）=Φ-1（1-q）作为阈值，即标准正态分布第（i·q/2p）百分位数，其中 qi= i·q/2p。由于打破了传统的单一惩罚，通过BH 方法确定的自适应阈值，对真实信号的稀疏性具有敏感性及适应性，且具有渐进最优性质。

类似于LASSO 方法，SLOPE 方法的解可以转化为如下优化问题

由式（4）得到的b 项是由相应的λi确定的，满足|b|(1)≥|b|(2)≥…≥|b|(p)，b 项相当于次序 L1范数。文献[10-12]中讨论了次序L1范数的凸性，相关的应用参见文献[13-15]。正如次序L1范数相当于L1范数的扩展，SLOPE 方法可以看作LASSO 方法的扩展。不同之处在于SLOPE 方法中不同的变量根据其相对重要性受到不同程度的惩罚，即对值较大的系数的惩罚比对值较小的系数的惩罚更大。在式（4）中，虽然SLOPE 方法在建立过程中借鉴了BH 方法的思想，但SLOPE 方法不是使用一个标量阈值来求解，因此即使在正交变量的情况下，这些过程也不是完全等价的。

2 在一般稀疏回归模型中的应用

2.1 在多重检验中的应用

本节展示了在一个具有特定相关结构的多重检验问题中，如何将SLOPE 作为一个有效的多重比较控制程序。考虑以下情况，医学家在5 个随机选择的实验室中各进行了1 000 个实验，得出的观察结果可以建模为

其中实验室处理效应τj独立同分布于正态分布随机误差项 zi，j独立同分布于正态分布且 τ 和 z 序列之间相互独立。相应的假设检验原假设为 H0，j：μj=0，则双边备择假设为 H1，j：μj≠0。对所有 5 个实验室的分数进行平均，结果是

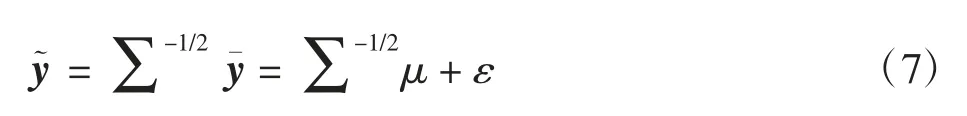
其中 ε～N（0，Ip），问题转换为经典的变量选择问题：识别回归系数向量μ 的非零组成部分，注意到Σ不是对角对阵，而Σ-1/2是对角占优的。如当σ2=1，ρ=0.5 时，解得通过选择Σ-1/2作为设计阵，可以将强正相关多重检验问题近似于正交设计下变量选择的问题，此时可以运用SLOPE 进行变量选择。

2.2 λ的选取

当设计阵的列是随机的相互独立的观测数据时，给变量选择的回归模型中引入了一系列复杂的因素，由于其具有随机性，列之间的内积不等于0。而偏离正交的情况会影响L1惩罚估计结果的一致性。SLOPE通过BH 方法确定的自适应阈值λ 是递减序列，类似于一个逐步下降过程，可以通过逐步修改合并λ 序列，削减由于相关变量收缩而产生的额外干扰。

类似于LASSO 方法中λ 序列的选择，假设X 的列有一个单位范数，且Z～N（0，1）。首先给出了LASSO方法的最优性条件

由 y=Xβ +Z 得

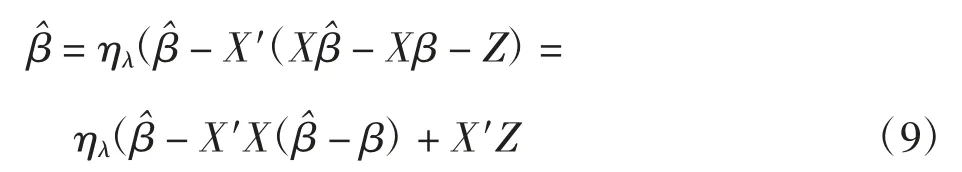
式中：ηλ为软阈值算子，ηλ（t）=sgn（t）（|t|-λ）+。记vi=则

记 S 为 βi的支撑集，XS为满足 βi≠0 的相关变量的子集，βS表示相应系数的值。根据式（10），为了找到Xi与非零集合之间的相关关系，考虑表达式假设βS和λ 的值的大小满足对任意正整数在不失一般性的条件下，进一步假设βj≥0。由于LASSO 方法中满足 KKT 条件

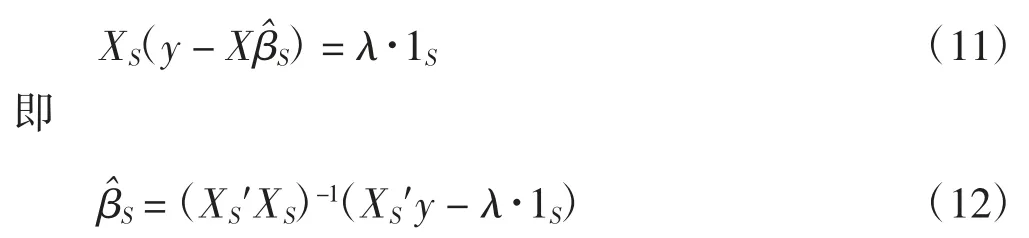
而对于 SLOPE 方法，λ 是一个非增序列（λ1，…，λp），而不是一个定值。将λ 序列代入上式，非零部分的估计值为

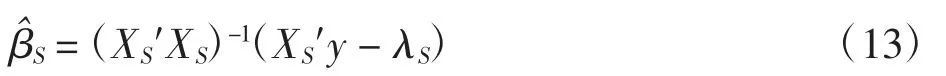
式中：λS=（λ1，…，λk）′，故由式（13）可得

在高斯设计下，设X 独立同分布于标准正态分布N（0，1/n），i∉S，则

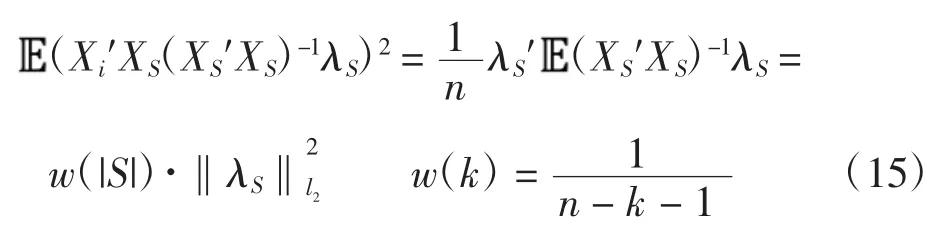
在 SLOPE 方法中，λ 是一个递减序列，其中 λBH（1）可以简单看作用于选取第一个进入模型的变量，选取λBH（1）=λG（1），而在下一步，由于选取λG（1）造成了回归系数的轻微收缩，需要考虑方差的轻微增加，故使用λG（2）代替λBH（2）

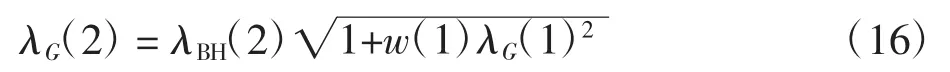
类似的，接下来选取λ3时需要考虑选取λG（2）和λG（2）造成回归系数的收缩，得到递推公式为

3 SLOPE 方法与LASSO 方法的比较

LASSO 方法通过使用L1范数作惩罚项，其本质是在最小二乘估计中简单地应用软阈值规则，选择的是一个固定的标量阈值。这相当于将所有p 值与一个固定的阈值λ 进行比较，转化为如下优化问题

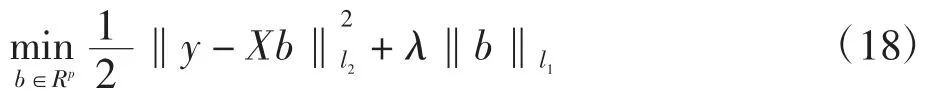
利用L1正则化项在零点的奇异性，将一部分不重要的变量系数的回归系数压缩到0。但由于使用L1范数造成的收缩，使得预测效果存在一定的偏差且预测精确度较低。

SLOPE 方法用排序后的L1范数作为惩罚项，相当于一个凸优化程序，在对回归参数进行估计的同时也实现了对变量的筛选，而且对参数估计比较大的变量回归系数也趋于增大。 但SLOPE 方法的思想与LASSO 完全不同，SLOPE 方法通过BH 方法得到的自适应的阈值对数据的稀疏性和大小很敏感，在控制FDR 达到名义水平的同时可以适应未知数据的稀疏性。同时通过修正λ 序列来平衡偏离正交性带来的影响，并可以运用到一般稀疏回归模型中进行变量选择。

接下来利用数值模拟方法分析比较SLOPE 和LASSO 方法拟合稀疏回归模型。首先，生成 X1000×1000为稀疏设计阵，其中设置非零变量数k 分别为10，20，…，50，令FDR 名义水平为q=0.1 时，运用R 程序分别使用SLOPE 和LASSO 方法进行变量选择，得到Lasso 和SLOPE 比较结果如表1 所示。

表1 LASSO 和SLOPE 比较结果

由表1 可以看出，SLOPE 和LASSO 方法都可以控制FDR 在名义水平下。其中对于非零特征数较少的情况，SLOPE 方法可以把所有非零元素准确识别出来，在非零元素个数增加时，在近百次的实验中分别出现了少数误判的情况，此时TPR 为0.98，预测效果较好，有较高的准确率。而LASSO 方法只有在非零元素较少时表现良好，随着非零元素的增多，无法适应数据的稀疏性，如非零元素为50 的情况，其平均只识别出14 个元素，控制FDR 在名义水平下，但TPR 只有0.28，无法在错误发现率和正确发现率中达到平衡，预测效果存在一定的偏差。相比之下，在一般情况下SLOPE 方法拟合稀疏回归模型效果更好，是一种准确且有效的变量选择方法。

4 实证分析

本文从Broad Institute 癌症项目数据集中选取了149 名乳腺癌患者，筛选出1 213 种与乳腺癌相关的基因表达数据作为样本①。记n=149，1 213 种基因分别记为 V1，V2，…，V1213，此时变量的数量远远大于观测值的数量，需要采取变量选择方法进行降维。分别运用SLOPE 和LASSO 方法来筛选数据，将一些无意义或者意义极小自变量的回归系数压缩至0，进行变量选择。设置FDR 名义水平为q=0.1，通过SLOPE 和LASSO 方法分别得到了46 和19 个非零回归系数，相应筛选出SLOPE 和LASSO 方法得到的显著基因变量如表2 所示。

为验证这2 种变量选择方法的有效性，通过主成分分析对数据集进行降维处理，得到的碎石图如图1所示。从图1 可以看出，折线图在43 个成分之后趋于平缓，即至少需要43 个变量才能包含90%以上的信息。

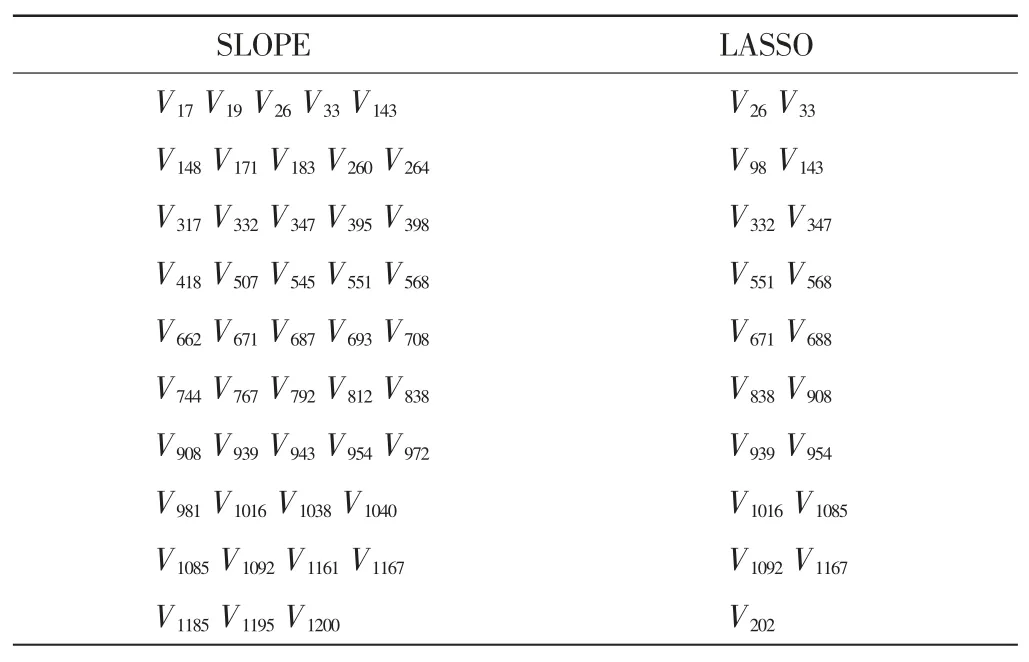
表2 SLOPE 和LASSO 方法得到的显著基因变量

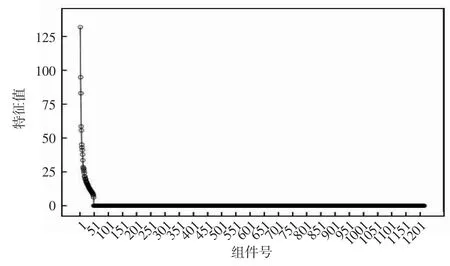
图1 主成分分析得到的碎石图

由表2 可知，LASSO 方法筛选出19 个显著变量，SLOPE 方法筛选出46 个显著变量，通过这2 种方法选择出来的相同变量有15 个。结合主成分分析结果，选取19 个变量最多只能包含原始变量65%左右的信息，选取46 个变量可以保留原始变量95%以上的信息。因此，可以推出相较于LASSO 方法过度压缩数据，SLOPE 方法可以更好地适应未知数据的稀疏性，有较高的预测准确性。控制q=0.1 时，SLOPE 方法得到的回归系数估计结果如表3 所示，其中对于相对更为显著的变量加上更大的回归系数。

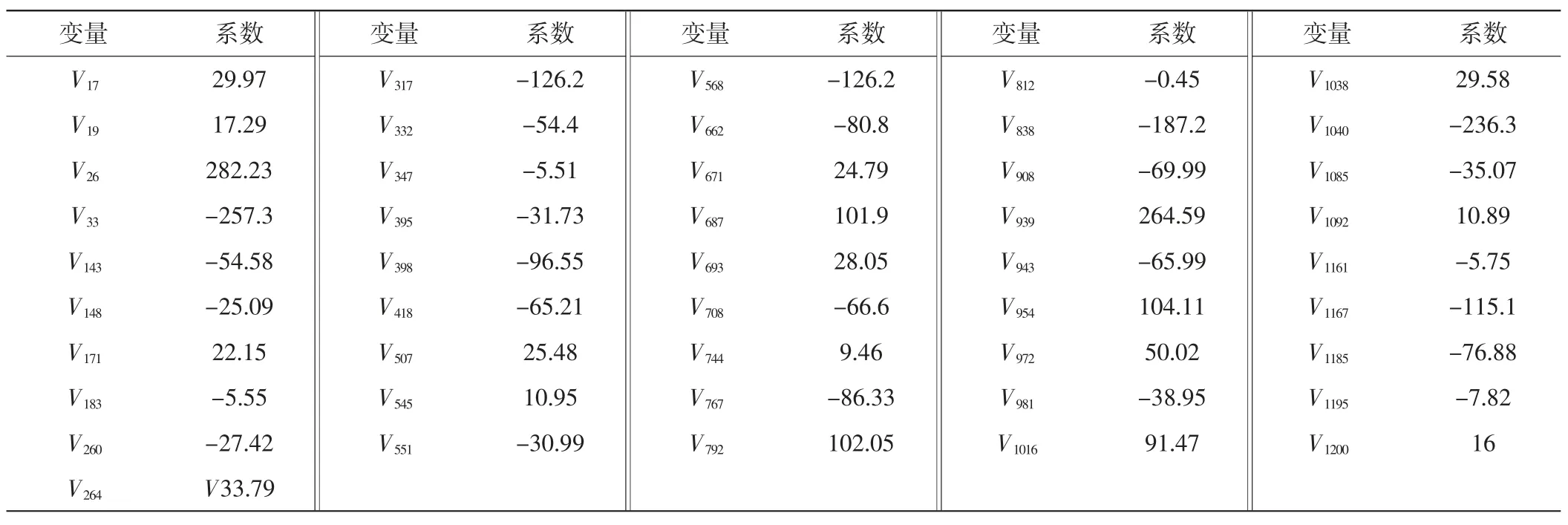
表3 SLOPE 方法得到的回归系数估计结果

表3 中回归系数的均值μ=-15.76，标准差σ=99.84，因此得到的回归系数具有显著性差异。且在SLOPE 方法选择出的46 个变量中，与LASSO 方法选择出的相同变量有15 个，此15 个变量用SLOPE 方法得到的相应的回归系数均为较大的值。由于SLOPE 方法对于更为显著的变量回归系数更大这一特性，可知在控制FDR 在名义水平q=0.1 时，LASSO 方法过于保守，只能筛选出较为显著的一部分变量，由于使用的是一个固定的阈值，无法很好地适应未知数据的稀疏性，导致了过度压缩数据。而SLOPE 方法使用的是基于BH 方法选择的自适应的序列，可以适应数据的未知稀疏性，在控制整体的错误发现率的同时，达到了增加势、控制第一类错误概率的目的，有更好的筛选效果。

5 结 语

本文基于SLOPE 方法研究对于高维数据的变量选择效果，通过数值模拟表明，相对于传统的变量选择方法，SLOPE 可以在控制整体的错误发现率的同时，适应未知数据的稀疏性。但使用SLOPE 分析超高维数据时仍存在算法运行缓慢、结果不够精确等问题，今后的工作可以结合交叉验证或样本拆分等方法提高方法的准确性和运行效率。

注 释：

① 数据来源 http：//portals.broadinstitute.org/cgi-bin/cancer/datasets.cgi。