二维正方晶格钨-硅橡胶声子晶体的带隙特性研究
2020-10-21郭翔鹰孙向洋朱雨男
郭翔鹰,孙向洋,朱雨男
(北京工业大学机械工程学院,机械结构非线性振动与强度北京市重点实验室,北京 100124)
0 引 言
声子晶体,是指由两种或者两种以上不同力学性能的材料构成的周期结构功能材料。此类材料存在声子带隙[1-3],某些特定范围频率的弹性波无法在其中传播。声子带隙的存在使得声子晶体结构具有广阔的应用前景,例如用于隔振减振、隔声降噪、制作声波滤波器、隔振器、波导装置等[4-9]。
国内外学者也对声子晶体结构进行了大量研究,主要集中在研究弹性波在声子晶体结构中的传播情况。例如,Sorokin 等[10]研究了自由平面波在无限长声子晶体结构中的传播。Romeo等[11-12]通过传递矩阵方法研究了一般三耦合声子晶体结构的自由波传播模式,讨论了当耦合参数趋于消失时波传播特性的演变。李建宝等[13]利用有限元法研究了微腔结构对二维声子晶体能带结构的影响。Huang等[14]研究了复杂声子晶体结构中波传播及其在智能结构半主动控制和健康监测中的应用。Shan等[15]研究了多孔声子晶体结构中弹性波的传播。黄海龙等[16]采用时域有限差分(FDTD)方法计算了铝梯度声子晶体结构复合木材的电磁波吸收特性。张昭等[17]采用平面波展开法研究了薄板型声子晶体的带隙及其减振特性。
对于声子晶体结构,重要的研究内容之一是其能带结构的计算,目前已经发展出了很多种计算方法,例如转递矩阵法、平面波展开法、时域有限差分方法、多重散射法、有限元法等[18-21]。这些方法各有利弊,传递矩阵法适用于一维声子晶体的研究[22],对于二维和三维较为复杂的模型则不太适用;平面波展开法思路清晰,计算效率高,可以用来计算二维声子晶体的能带结构[23];时域有限差分方法可计算较为复杂的模型[24],但其计算量较大;多重散射法理论推导较为复杂,且只能用于简单的圆柱及球形散射体单元结构的声子晶体[25];有限元法不但能直接计算声子晶体的能带结构[26],也可快速计算其传递损失。综上所述,本文采用平面波展开法和有限元法相结合计算二维正方晶格固/固型声子晶体的能带结构与传递损失,并对于在能带结构中出现的特殊现象进行分析。
1 模型介绍
由于晶体的周期性,对于理想的无限周期的声子晶体只需要研究一个单胞即可[23],如图1(a)所示,这个二维正方晶格单胞由圆形散射体和正方形基体组成,材料分别为钨和硅橡胶,晶格常数为a,散射体半径为r, 散射体的填充率为f=πr2/a2。利用有限元软件Comsol中的平面应变单元进行网格划分。然后根据Bloch定理,在单胞的上下左右四个边界分别应用Bloch周期性边界条件如图1(b),其边界位移满足ui(x+a,y+a)=ui(x,y)e-i(kxa+kya)(i=x,y),其中u为位移,k为波矢。当波矢沿着第一布里渊区的边界取值时,即沿着Γ-X-M-Γ方向扫描如图1(c),通过求解本征值问题,得到结构的特征频率,进而得到声子晶体能带图。
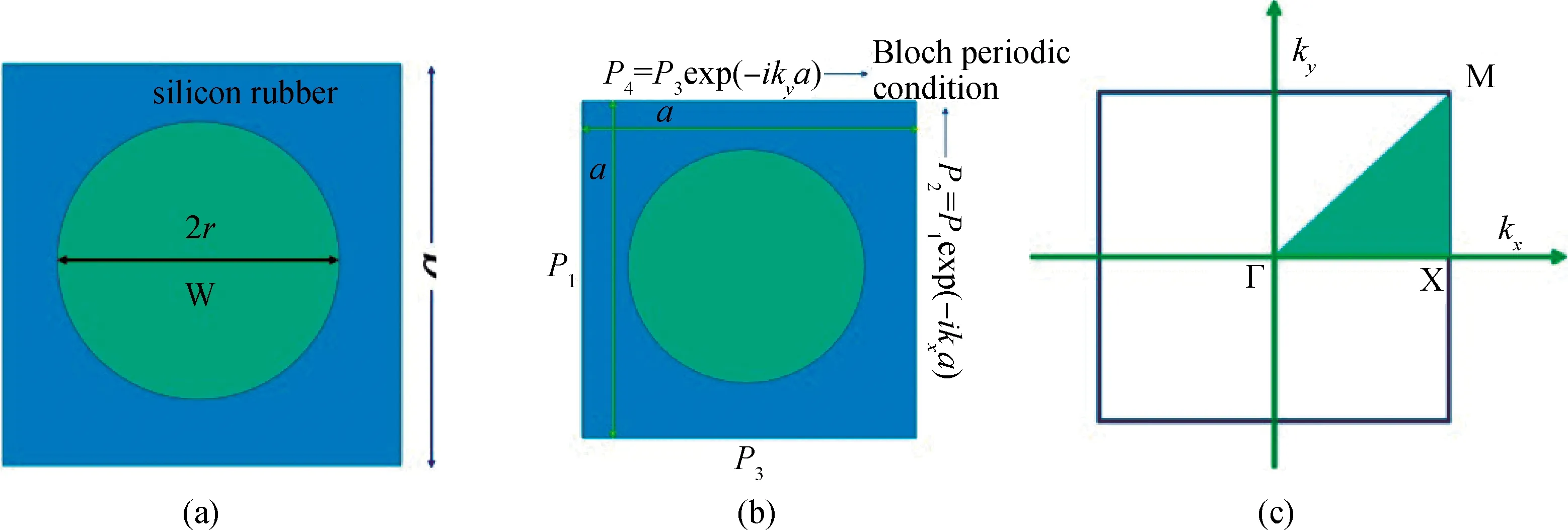
图1 (a)单胞示意图;(b)边界条件关系;(c)第一布里渊区Fig.1 (a)A cell diagram;(b)a boundary condition relationship;(c)the first Brillouin region
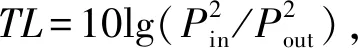
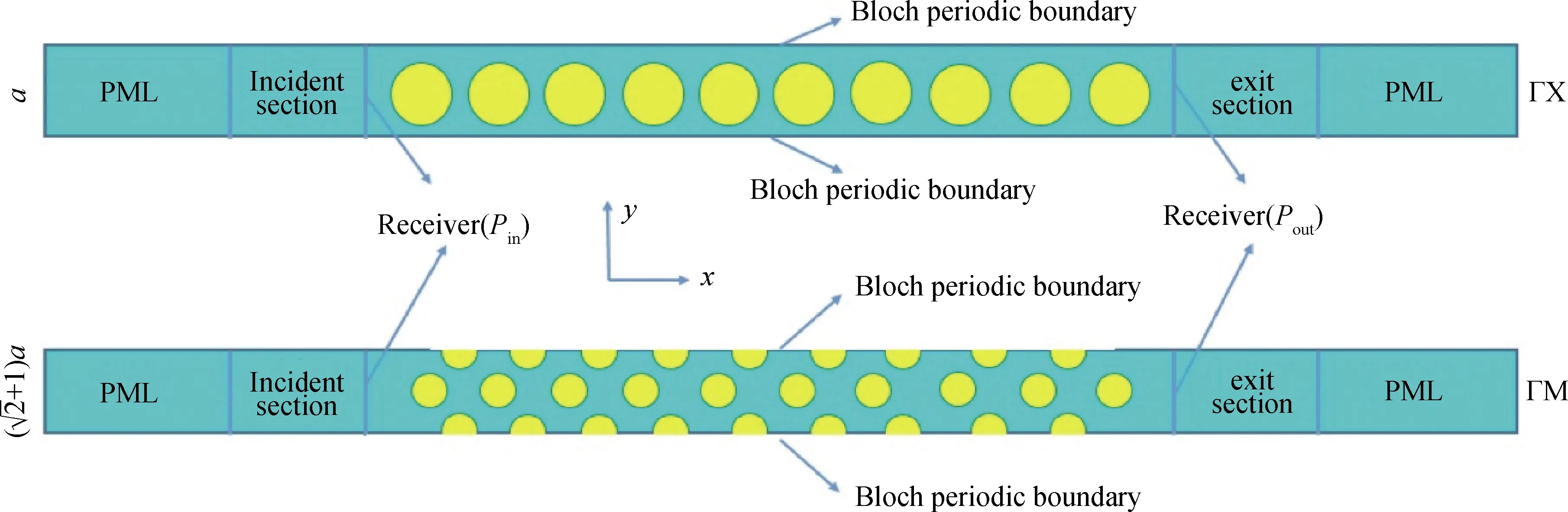
图2 用于计算传递损失的包含10行单元的有限结构Fig.2 A finite structure containing 10-line elements for calculating transfer losses
2 平面波展开法简介
平面波展开法是声子晶体研究中最常用的方法之一,能够用于不同维数声子晶体的弹性波带隙计算,并且其概念清晰,计算量小。它的基本思想是利用声子晶体结构的周期性,将声子晶体的材料参数和结构参数按照傅里叶级数展开,再在倒格矢空间进行平面波叠加,通过求解近似值,从而得到其能带结构。由于声子晶体的结构周期性,拉梅常数λ和μ以及密度ρ都是空间r=(x,y)的周期函数,拉梅常数与杨氏模量E和剪切模量G之间的关系为

(1)
各参数均可按照傅里叶级数展开。为叙述方便,统一使用h来表示这三个参量
(2)
式中,G为倒格矢,进一步的通过在倒格矢空间进行平面波叠加,选取钨和硅橡胶声子晶体的结构函数,结合Bloch定理,求出此类周期结构的本征方程如下:
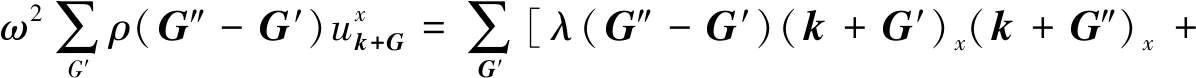
(3)
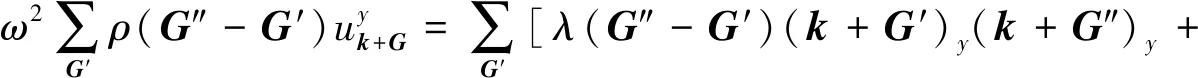
(4)
方程式(3,4)为无限阶复数矩阵的特征值问题,其中G′取遍整个倒格矢空间,ω为周期性结构的角频率,k为波矢量。下面基于得到的本征方程式进行Matlab编程,选取441个平面波波数,通过求解近似值,从而得到钨-硅橡胶声子晶体的能带结构。
3 结果与讨论
3.1 能带结构计算
取单胞结构的散射体半径为4 mm,晶格常数为10 mm。材料参数如下表1所示。

表1 材料参数Table 1 Material parameters
计算得出二维钨-硅橡胶声子晶体的单胞能带结果如图3所示。从计算的结果可得,平面波展开法计算的第一完全带隙范围为382~997 Hz,带宽为:615 Hz,其中心频率为689.5 Hz。同时,利用有限元法计算得出上述模型的第一完全带隙范围为396.9~1 009.4 Hz,带宽为:639.5 Hz,其中心频率为703.15 Hz,因此两种方法计算得出的结果基本吻合,验证了本文采用平面波展开法计算结果的正确性。
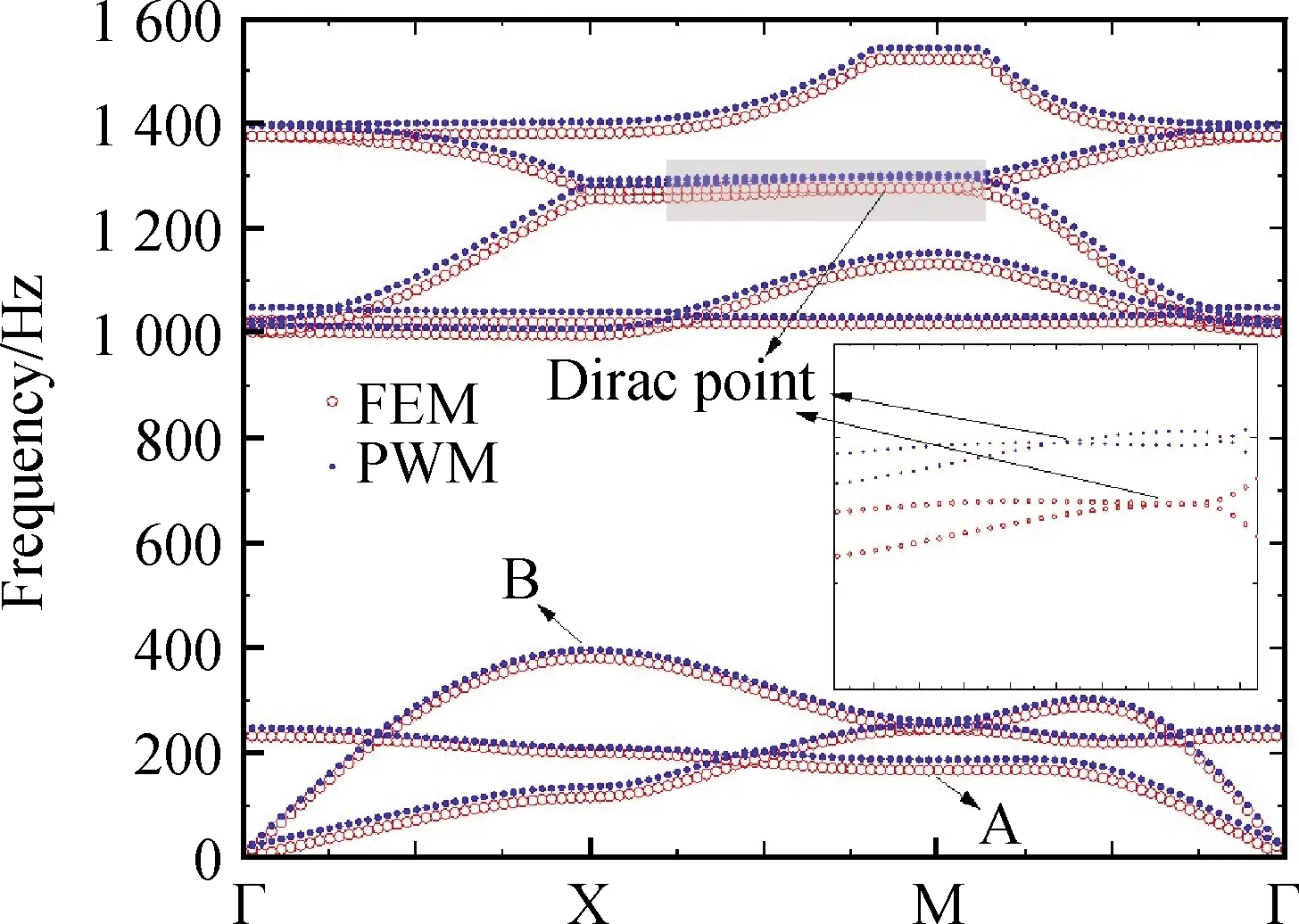
图3 二维钨-硅橡胶周期性结构能带图Fig.3 Two-dimensional energy band diagram of periodic structure of tungsten-silicone rubber
从图3得出的带隙频率范围发现,由硅橡胶-钨组成的正方晶格的声子晶体在第一布里渊区存在多条不完全带隙,同时在中低频的范围能出现声子禁带,对工程上的中低频隔振器的设计有一定的理论指导作用。并且在布里渊区边界XM方向,第六条和第七条能带相交,并且形成了一个两重简并的狄拉克点。同时在XM方向之外,其他方向都是以禁带的方式存在。为了清楚的看出狄拉克点的存在,局部放大阴影部分,可看出无论是平面波展开法还是有限元法都存在狄拉克点,只是位置稍有不同。
为了进一步分析在能带结构中出现狄拉克点的原因,图4中计算了二维钨-硅橡胶声子晶体在狄拉克点频率下的双重简并态的本征场图,图4(a)表示的是偶极子态,图4(b)表示的是四极子态,而偶极子态和四极子态都是双重简并态,因此本征场显示的结果与能带图是吻合的,这种双重简并导致了狄拉克点的出现。
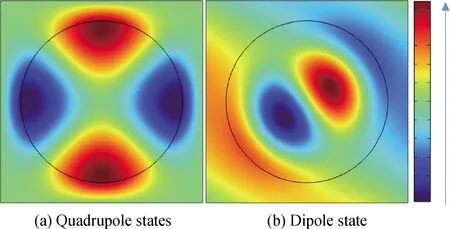
图4 结构的本征态压力场Fig.4 Eigenstate pressure field of structure
前面已经得出二维钨-硅橡胶声子晶体的单胞能带结构,为了验证对于有限个单胞组合的超胞结构是否具有同样的声子禁带,应用了如图2所示的含10个单胞的钨-硅橡胶声子晶体超胞模型,用于其传递谱的计算,得出该结构的传递损失如图5所示,a区域为禁带,此禁带范围为475~1 000 Hz,带宽为525 Hz,中心频率为737.5 Hz,与之前得到的单胞能带计算结果基本吻合。证明对于二维钨-硅橡胶声子晶体,其单胞与超胞的禁带范围是一致的,对于单胞的研究情况可以推广到超胞结构,这对于简化计算过程极为有利。

图5 超胞结构的传递损失Fig.5 Transfer loss of supercellular structure
为了能够更加直观呈现频率与波矢之间的关系,图6计算了二维钨-硅橡胶声子晶体的第一能带三维图及其二维云图,得到在高对称点的位置,波矢的频率为0,而在XM方向上波矢则存在较大的频率。
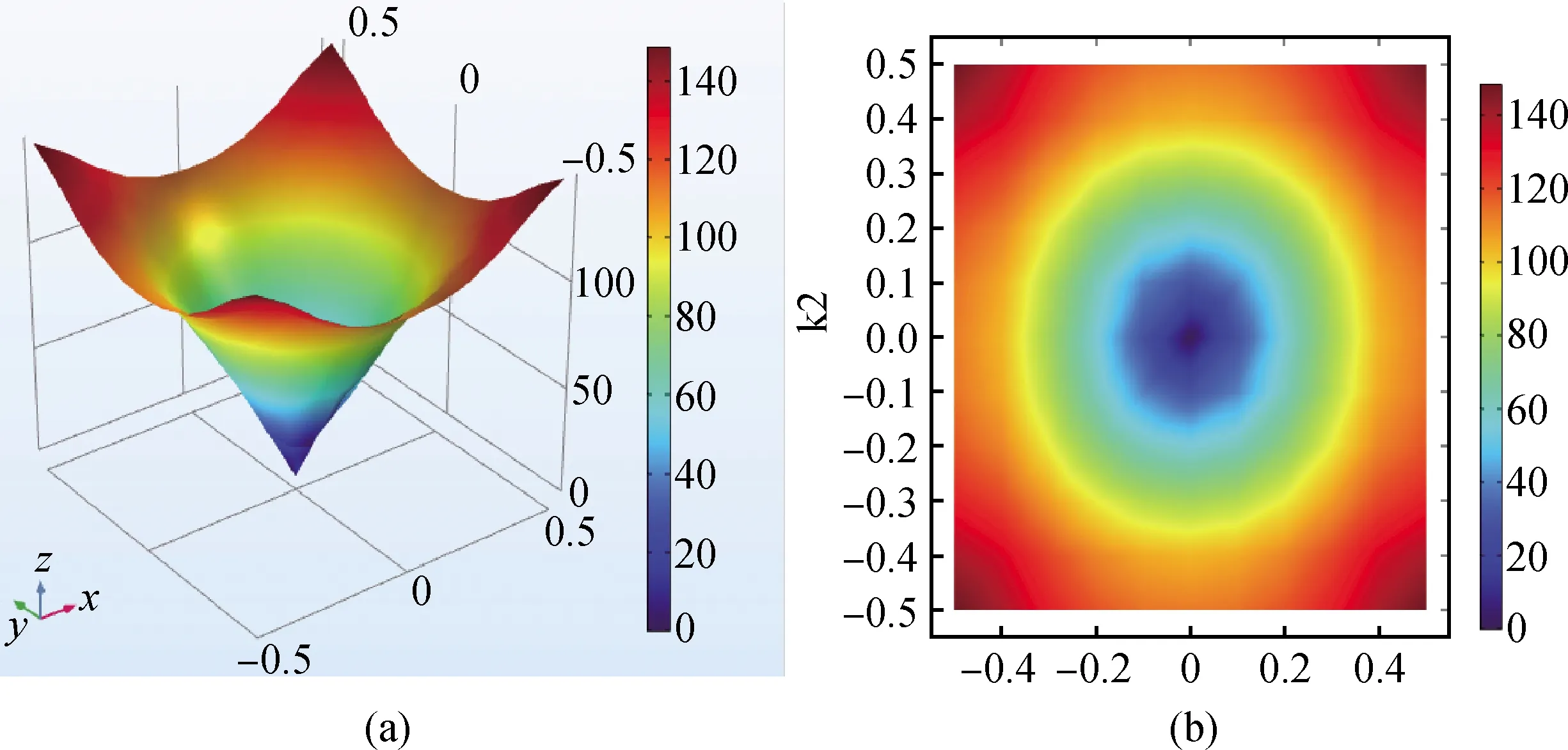
图6 第一能带三维图(a)及其二维云图(b)Fig.6 Three-dimensional map(a) of the first energy band and its two-dimensional cloud map(b)
进一步研究在不同的模态下二维正方晶格钨-硅橡胶声子晶体结构的变形趋势,图7(a)和图7(b)分别计算单胞的模态A总位移变化趋势图和模态B的总位移变化趋势图(对应于图3中的模态A和模态B),发现模态A主要发生扭转变形,模态B主要发生剪切变形。从云图的计算得出对于模态A,其单胞的中心位置与四个边角位置变形较小,而散射体与基体的连接处变形较大。对于模态B,其单胞的四个边角位置变形较大,而散射体整体的变形较为均匀。因此,对于扭转变形而言,散射体与基体相连接处为应力集中区,而剪切变形对散射体的影响则不明显,因此工程应用中散射体与基体的连接部位则需要加固设计。

图7 总位移的变化云图Fig.7 Change of total displacement nephogram
3.2 材料参数对带隙的影响
对于声子晶体结构而言,其材料参数对声子带隙的影响非常重要,所以下面选取了10种不同的散射体材料(表2给出了各种材料的参数)研究二组元声子晶体结构中材料参数对其带隙特性的影响,包括散射体与基体的密度比、杨氏模量比对第一完全带隙的影响,以及两者之间的关系。
图8研究了不同密度比对二维正方晶格固/固型声子晶体的第一完全带隙的影响情况,从图8可以看出,随着密度比(散射体密度与基体密度的比值)的增大,第一完全带隙的起始频率逐渐增加,但是截止频率变化较小,带宽逐渐减小。对于工程上的低频隔振结构来讲,通过选取合适的材料,使得材料间的密度比减小,可获得较低的隔振频率以及较大的隔振带宽。图9显示了二维固/固型声子晶体的第一完全带隙与杨氏模量比(散射体的杨氏模量与基体的杨氏模量的比值)没有明确的关系,随着杨氏模量比的增大,第一完全带隙有增有减,不呈现出特定的规律。通过密度比与杨氏模量比对第一完全带隙的影响分析,得出:密度是影响带隙特性的决定性因素之一,调整两组分材料的密度比能改变二维固/固型声子晶体的带隙特性。
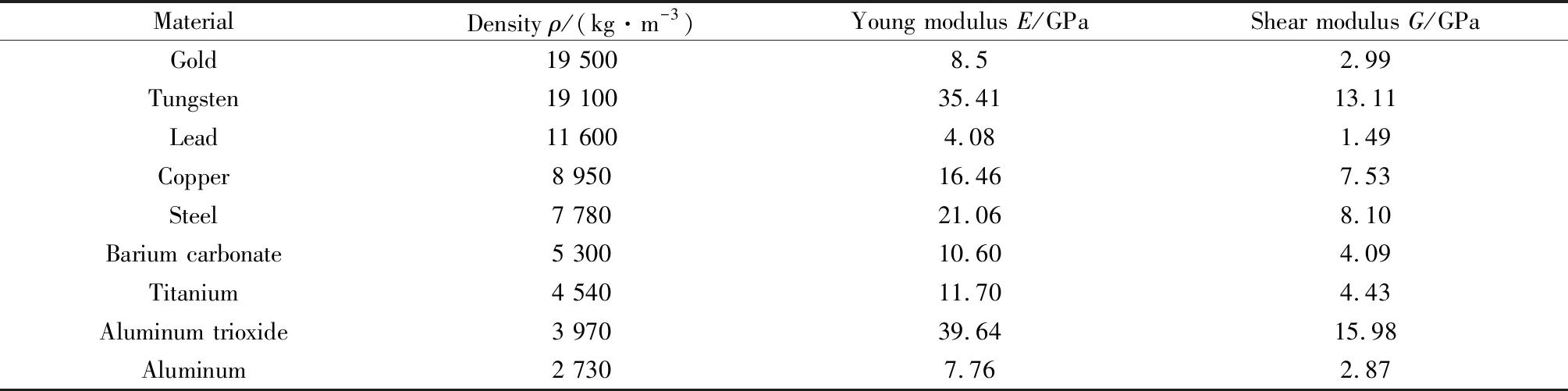
表2 不同散射体材料的各项参数Table 2 Various parameters of different scatterer materials
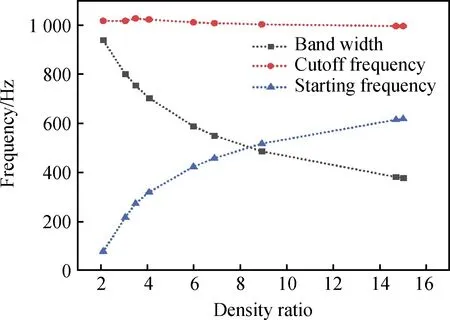
图8 第一完全带隙与密度比的关系Fig.8 Relationship between the first complete band gap and density ratio

图9 第一完全带隙与杨氏模量比的关系Fig.9 Relationship between the first complete band gap and Young’s modulus ratio
4 结 论
本文计算了二维正方晶格钨-硅橡胶声子晶体的能带结构,并对其中出现的特殊现象进行分析,研究了出现狄拉克点的原因,同时分析了材料参数对该能带的影响情况。综合以上研究,得出以下结论:
(1)由钨-硅橡胶组成的声子晶体结构在中低频的范围能出现声子禁带。
(2)散射体与基体相连接处容易出现应力集中现象,工程应用中散射体与基体的连接部位需加固设计。
(3)随着密度比的增大,二维钨-硅橡胶声子晶体的第一完全带隙的起始频率逐渐增加,但是截止频率变化较小,带宽逐渐减小,通过调整材料的密度比将显著地改变声子晶体结构的带隙特性。同时,第一完全带隙与杨氏模量比没有明确的关系。
