预判指引 事半功倍
2020-10-20常建伟
常建伟
[摘 要] 平面解析几何综合题综合性强,运算过程复杂,方法灵活多变. 有的学生在解题过程出现思路受堵,运算烦琐. 学会借助预判思维指引解题,通过目标预判,明确解题方向;通过方法预判 优化解题策略;通过结果预判,修正解题过程,从而有助于既快又准地解题.
[关键词] 解析几何;预判思维;圆锥曲线
平面解析几何综合题可与函数、方程、不等式、三角、向量、平面几何等知识交汇考查,往往题目综合性强,运算过程复杂,方法灵活多变. 解此类题型时,有的学生思维方向容易迷失,无从下手;有的学生方法选择不当、运算准确性不够. 若在解题过程中能合理运用预判思维,有助于引领思路,优化解题过程,甚至达到事半功倍的效果. 下面就以解答平面解析几何综合题为例,从三个方面谈谈预判思维在解题中如何合理使用,希望对学生的解题有所启示.
目标预判,明确解题方向
在解决存在性、探索性等问题时题目未明确给出结论时,我们要充分挖掘题目条件,整体建构好解题思路,采用特殊化、极端化等方法预判出可能结论,将不确定性问题进行目标明确化,再进行结果验证.
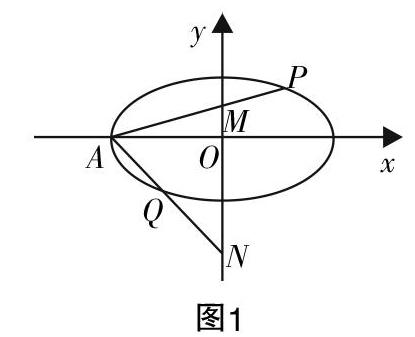
例1:在平面直角坐标系xOy中,椭圆C:■+■=1的左顶点为A,点P,Q是椭圆C上的两个动点.
(1)如图1,当P,O,Q共线时,直线PA,QA分别与y轴交于M,N两点,求证:■·■为定值;
(2)设直线AP,AQ的斜率分别为k1,k2,当k1k2=-1时,证明:直线PQ经过定点R.
试题分析:本题第一问求■·■是定值,可以通过特殊法先预判出定值结果,由于P,Q两点的运动变化性,不妨取P,Q两点为短轴的两端点,则P,Q两点即为M,N两点,得■·■=1. 具体写解题过程时可设点P(x0,y0),Q(-x0,-y0),再将M,N两点坐标求出,可得■·■=4+■=1. 第二问若采用一般性解法,先设斜参求出直線PQ的方程,然后化简方程,结合直线系的思想与参数无关进行求解定点,不少学生解题时往往在最后求定点时“卡壳”,因方程复杂,目标定点不明确,无从下手,少数学生的运算基本功扎实、式子处理能力强也能求解.若能结合预判思维,问题便能迎刃而解.由椭圆的对称性可预判直线PQ过定点,在x轴上,采用特值探求,可令xp=xq或令k1=1,k2=-1,则可求出直线PQ与x轴交点坐标,既直线PQ过定点-■,0,最后用一般化方法验证. 验证的过程便体现了解析几何的思想:用代数的方法研究几何问题.
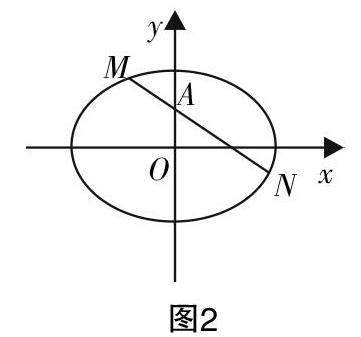
例2:如图2,过椭圆C:■+■=1内一点A(0,1)的动直线l与椭圆相交于M,N两点,是否存在与点A不同的定点B,使得对任意过点A(0,1)的动直线l都满足■·■=■·■?若存在,求出定点B的坐标;若不存在,请说明理由.
试题分析:本题是探索性问题,按常规思路设点直接求解,参数较多,运算复杂,解题很难走到最后.若能打开思维,充分挖掘条件中蕴含的几何特征,便能预判出可能的结论. 假设点B存在,先取直线l平行于x轴时,由几何特征知点B在线段MN的垂直平分线即y轴上,再取直线l垂直于x轴,可得点B的坐标只可能是(0,2),然后进行一般性验证.本题中的一般问题特殊化是破题的关键,也是解析几何直观性的体现.
方法预判,优化解题策略
解答解析几何综合题时为优化解题,降低运算难度,常会面临着点参、斜参、角参的选择. 学生在解题时要掌握解析几何的思维特征和基本思想,根据题设的几何特征,灵活运用曲线的有关定义、性质,结合自身已有方法经验选择合适的参变量、公式、坐标系进行解题预判,从而做出更合理的解题策略选择.
例3:在平面直角坐标系xOy中,已知椭圆C:■+■=1,过椭圆的左顶点A作直线l⊥x轴,点M为直线l上的动点(点M与点A不重合),点B为椭圆右顶点,直线BM交椭圆C于点P,求证:AP⊥OM.
试题分析:问题中要证明AP⊥OM,斜率积和向量数量积两个角度都可以刻画垂直关系,但都需求出点P和点M的坐标,此处涉及参数的选择的问题,可直接设点参求解,也可设斜率参数表示点的坐标. 本题解题方法比较多,如何选择相对能优化解题过程,减少运算?可做出以下解题方向预判. 若设点参解题,则选择点M较好,由于点M横坐标已知,然后求出直线BM与椭圆交点P;若设斜率参解题,则直接将点P通过斜率参表示出来求解;若能进一步发现A,B两点关于原点对称,由圆锥曲线“第三定义”知kPA·kMB=kPA·kPB=-■,可直接将直线AP,BM用同一个参数k表示,则本题可得到快速求解.不过还是要提醒学生注意,一旦解题目标确定,预判方法可行,就要坚持算下去,有时坚持比方法更重要.
例4:已知椭圆■+■=1,设直线l:y=kx+m(k≤■)与椭圆C相交于A,B两点,以线段OA,OB为邻边作平行四边形OAPB,其中顶点P在椭圆C上,O为坐标原点,求|OP|的取值范围.
试题分析:本题是直线与椭圆的综合问题,求OP的取值范围需将点P的坐标表示出来. 在平行四边形OAPB中,■=■+■,则点P坐标为(xA+xB,yA+yB). 将直线代入椭圆方程得到关于x的一元二次方程,再结合条件列出|OP|关于k,m的函数,进行求解处理时发现再消参困难,运算烦琐,容易出错,甚至解题受阻. 那用设点法能不能处理呢?做出以下预判,将题目条件重新组合,通过点P与点A、点B的坐标关系,联想到点差法,可将点P的坐标与斜率k的关系找出来,再结合椭圆方程即可求解点P的坐标. 本题答案:■≤OP≤■.
结果预判,验证解题过程
对解题过程中的一些阶段性结果的准确性进行预判,若与解题目标不符,则及时修正调整.
例5:已知圆A的方程为(x+1)2+(y-2)2=20,过点B(-2,0)的动直线l与圆A相交于M,N两点,Q是MN的中点,直线l与l1相交于点P,直线l1的方程为x+2y+7=0.(1)当MN=2■时,求直线l的方程. (2)■·■是否为定值?如果是,求出其定值;如果不是,请说明理由.
试题分析:有的学生在第一问出现少解情况,错误的原因是设直线方程时未考虑斜率不存在的情况. 其实解题过程中通过结果预判可及时发现错误.因为点B在圆内部,而弦MN不是直径,所以这样的直线肯定有两条. 我们平时在解题时需要适当停顿,借助几何直观,明确算理,多一点思考,便会少出错.本题的第二问可以采用特殊法进行结果预判检验运算的准确性. 本题答案: (1)x=-2或3x-4y+6=0;(2)■·■为定值-5.
例6:在平面直角坐标系xOy中,已知椭圆■+y2=1,左、右两个顶点分别为A1,A2. 过点D(1,0)的直线交椭圆于M,N两点,直线A1M与NA2的交点为G,求证:点G在一条定直线上.
试题分析:本题首先可以进行解题目标预判,若过点D的直线交椭圆于M,N关于x轴对称的M′,N′两点,则直线A1M′与A2N′的交点为G′,由椭圆的对称性,可得GG′所在定直线应是与x轴垂直的直线. 由于A1,A2是椭圆左、右顶点,可分别设直线A1M与A2N的方程,并与椭圆联立方程组求出M,N的坐标,利用M,D,N三点共线写出两斜率关系,进一步得到点G的纵坐标是定值.为了验证运算结果的准确性,可取MN垂直于x轴时将点G的坐标求出验证. 本题也可以采用先特殊再一般的方法求解,由椭圆的对称性先预判定直线为x=4,然后设直线MN的方程为x=my+1. 再证明对于任意的实数m,直线A1M与直线A2N的交点G均在直线x=4上.
综上所述,预判思维在解答解析几何综合题的过程中有着显著的作用,当然预判的结论不一定都是对的,学生需要平时加强知识经验的积累和方法的总结,以便做出相对准确合理的预判,从而有助于指引解题的方向,优化解题的策略,修正解题的结果,实现既准又快地解题.
