提升数学作业设计有效性的策略研究
2020-10-20杨西梅
杨西梅
[摘 要] 文章以高中数学作业设计这一环节为切入点,从作业设计的趣味性、典型性、层次性、实践性和开放性五个方面着手,为提升作业有效性和教学质量探索出一条有效途径.
[关键词] 数学作业;有效性;创新
数学作业是整个数学教学中的重要一环,也是教师十分关注的教学问题,更是提升教学效果的关键所在. 但在我们平时的教学中,存在着很多“乱”象,一些内容重复、毫无新意、超载负荷的作业占据着整个课堂,这样的作业设计不仅缺乏教学责任心,而且会消耗学生的精力和兴趣,与新形势下的“减负”背道而驰. 因此,要提升作业的有效性首先就需要提升作业设计的有效性. 笔者在多年的数学教学中,对数学作业的有效性有了一定的策略思考,并作以下整理.
增添趣味性,激趣探索重创新
兴趣是最好的老师,课堂教学需要激趣,作业设计亦是如此. 新课程理念下的数学作业设计需要更多地关注学生的具体学情,不能仅仅停留在机械记忆或是重复模仿上,我们可以在设计的过程中针对不同的教学内容去设计不同形式的作业,尽可能地选择一些与学生实际联系密切的或富有创造性的题目,这样的荤素搭配能打破传统的作业模式,为学生的探究增添一丝趣味. 这样一来,即可摆脱枷锁繁重和枯燥乏味的“囚笼”,让学生产生好奇、乐于探究,让作业过程趣味横生,并迸发创新思维火花.
案例1:以“集合”这一章节的作业设计为例
作业1:尝试写一篇拟题为“空集的自白”的数学周记,或尝试出一份以“空集”为主题的手抄报,又或是以本章内容为主要内容制作多媒体演示文稿等.
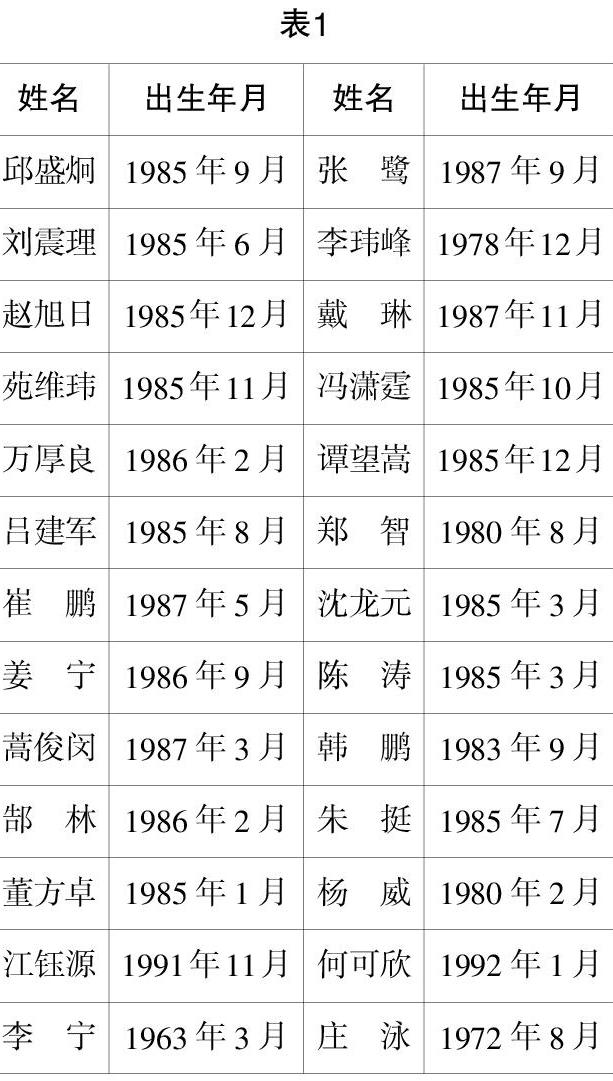
作业2:表1为部分国家级运动员的个人信息:
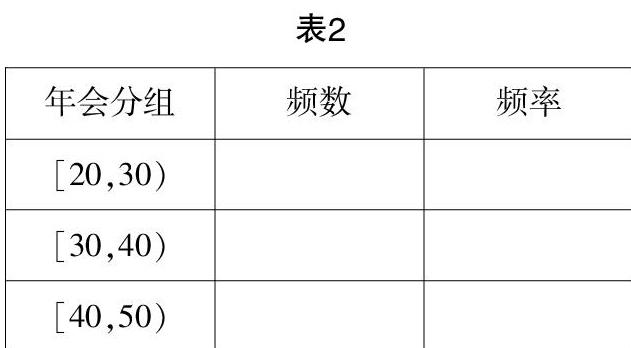
(1)试根据表1中的信息,填写以下频率分布表(见表2):
(2)估一估以上运动员中年龄在25岁以下的约占百分之几;
(3)尝试绘制以上26名运动员的年龄频率分布直方图.
这样的作业增加了形式的多样化,提升了内容的趣味性和灵活性,这样的作业比机械答题更有趣,同时助长了学生思维的主动性,丰富了学习体验,进一步提升了思维层次和数学素养.
彰显典型性,事半功倍提效率
不少教师处于功利性目的的需要,数学作业总是安排一道又一道的习题,以此推广一种又一种的解题方法,并不关注是否有效. 事实上,相较于小学与初中学习,高中由于学科变多,一切时间都显得十分宝贵,显然以上这样的题海战术是不适用的,也是低效的、无奈的. 因此,在设计作业时,需本着减负增效的理念,在选题和编题上狠下功夫,确保彰显作业的典型性和代表性,进而事半功倍地提高效率.
案例2:以“均值不等式”这一内容的作业设计为例
作业1:已知实数a,b,x,y满足a2+b2=1,x2+y2=1,试求出ax+by的最大值.
作业2:已知实数a,b,x,y满足a2+b2=16,x2+y2=36,试求出ax+by的最大值.
评析:作业1与作业2是两道具有较大深意的数学问题,虽然看似简单、类似,却令人回味无穷. 作业1是一道“一题多解”的题型,若能把握问题本质,则可探究得出多种解法;再来解决作业2,不少学生感觉其与作业1相同,于是接近半数以上的学生将答案错解成26,其具体的解题过程为:因为ax≤■,by≤■,所以ax+by≤■=26. 这样的解题思路显然是错误的,通过典型错误即可激发学生的深思熟虑.
以上作业中的两个典型例题是教师精心选择的,两个例题都在纵向复习的过程中加深了知识的横向沟通,能激励学生积极探索,获取隐含的知识内蕴,以达到磨砺思维、发展智力、刺激求知欲望的多重目的,这也是创新教育实施的良好措施,提升课堂效率的有效手段.
体现层次性,因人而异促发展
一个班级的学生人数众多,由于受到智力或非智力因素的影响,每个学生在学习水平上也会参差不齐. 对于不同水平的学生,日常的学习任务需要有所区别,作业自然也不能采用“一刀切”来造成学习负担,而需充分考虑不同层次学生的实际需求设计分层作业,可以深化对知识的理解,促进不同层次学生的发展,同时也有助于“低负、高效”的有效实现.
案例3:以“一元二次不等式解法”的作业设计为例
作业:(A层)解以下不等式:
(1)4x2-4x>15;
(2)14-4x2≥x;
(3)x(x+2) (4)-x2-2x+8≥0. (B层)求以下函数的定义域: (1)y=■; (2)y=■; (3)y=■. (C层)已知不等式kx2-2x+6k<0(k≠0). (1)若不等式的解集为{xx<-3或x> -2},试求出k的值; (2)若不等式的解集为R,试求出k的值. 评析:对于A层的学生,以上问题的设计主要在于基础性问题的训练,使其在适当难度问题的反复训练中梳理答题思路,尽量使他们“吃得下”;对于B层的学生,以上问题的设计主要关注到基础性问题的变式训练,通过稍有难度的问题训练提升学习积极性;对于C层的学生,以上问题的设计关注到能力的提升和综合问题的解决,以满足其较强的求知欲,使他们“吃得饱”. 这样的作业设计,充分调动了学生的积极性,使每个学生都练有所获,既兼顾了学困生,让他们的作业“会做”,又为学优生提供了创造和表现的机会,让每个学生都获得充分的成功体验,从而有效贯彻“因材施教”的教学原则. 关注实践性,实践应用促发展 数学作业应当与数学学习内容以及学生的生活有着密切的关系,若断掉这层关系,数学作业有何意义?学生完成的价值意义何在?从当今人才培养的角度来看,教师需拓展教材的时空局限,设计具有一定的实践性的数学问题,为学生搭建实践活动的平台,让数学问题具有“生活味”,促进综合素养的发展. 案例4:以“研究性学习”的作业设计为例 作业1:随意选择测量工具和测量方法去测量学校旗杆的高度. 作业2:利用課余时间,分组调查某银行推出的按揭购房的两种还款方式——等额本金还款法以及等额本息还款法,并尝试解决以下问题:张芳在某银行按揭贷款5万元,还款期限为10年,且月息为4.65‰,试求出等额本金还款法与等额本息还款法每月各应还款多少元;并思考,从自身的家庭经济收入出发,应选择哪一种还款方式. 这样的作业设计符合新课程所倡导的“数学源于生活并服务于生活”的教育理念,让学生在实践中学习、合作、创新,在实践中感受数学知识的应用价值,在实践中体会数学知识的无限魅力. 凸显开放性,思维求异妙提升 在作业设计中,只要把封闭式的作业加以改良,即可生成具有挑战性的开放式作业,有效增强学生的参与意识,为学生的思维创设一个更加广阔的空间,激发多方位、多角度的分析和探究,让学生会思、善思、巧思,提升探究能力、创造能力和想象能力. 案例5:以“椭圆的标准方程”的作业设计为例 作业:以原点O为中心的椭圆,满足以下条件:①焦点F1的坐标为(3,0);②长半轴的长是5,则可求出椭圆方程为■+■=1. 改变什么条件,可使求出的椭圆方程仍不变? 学生经过思考得出以下结论:①短半轴的长为4;②离心率e=■;③右准线方程为x=■;④点P3,■在椭圆上;⑤椭圆上两点间的最大距离为10…… 通过这样一道开放性问题,引导学生去思考、去探究、去改编,让学生在探索的过程中深刻理解椭圆的一些基本量,为学生提供张扬个性和自主创新的空间. 在这个过程中,不同层次的学生都能参与问题的解决过程,知识巩固的目标达成了,学生的自主性和创造趣也得到了培养. 总之,上述作业设计的形式并非孤立存在的,还可以交替联合使用,无论哪一种形式的作业设计,设计理念都是为了与新课程理念相融合,让学生喜欢学数学,主动做数学,从而真正提升课堂实效性.
