地震作用下矿山边坡永久位移非线性分析

蒋 魁，王 帆，蒋兴中，景鹏旭

(1.中国有色桂林矿产地质研究院有限公司，广西 桂林 541004；2.桂林矿产地质研究院工程有限公司，广西 桂林 541004；3.广西壮族自治区第一地质队，广西 桂林 541004；4.中国地震应急搜救中心，北京 100049)

当前研究矿山边坡稳定性时，关于岩体非线性强度特征及其对边坡稳定性影响的相关研究尤为重要。现场勘测结果表明：边坡后侧岩体的拉应力区域会显著影响矿山边坡的稳定性。关于抗拉强度的研究发现[1]，采用两种方法可以有效地分析边坡拉应力区的抗拉强度，使分析结果更加趋于真实的破坏条件，其一是对岩土体的抗拉强度进行一定程度的折减，即将线性破坏曲线优化为非线性强度包络线；其二则是在边坡后缘的拉应力区引入不同形态的裂缝。 对于后者考虑裂缝的存在，MICHALOWSKI[2]将裂缝的扩展过程与整体的滑落状态结合，研究结果表明：对于高陡边坡或受静水压力影响显著的边坡，裂缝的存在大大增加了失稳的风险。UTILI[3]分析了预设垂直裂缝边坡的地震稳定性的影响，研究显示地震荷载对边坡的稳定性影响尤为显著。对于前者所考虑的抗拉强度折减方法而言，当前的处理方式，大多在变分法或极限分析法的基础上进行。BAKER等[4]对拉剪区域进行了一定的折减，并结合变分法对强度包络线中的张拉区域进行了相关的稳定性分析。PARK等[5]以极限分析上限法为理论基础，选择圆弧对经典M-C准则中的强度包线进行优化，讨论了岩土体的抗拉强度的变化对边坡稳定性和破裂形态的影响。 在使用极限分析法时，仅需对边坡达到极限平衡状态时候进行计算，计算过程相比有限元法更加简洁，且计算速度快。

地震的作用往往是诱发边坡失稳的直接因素，TERZAGHI[6]提出了拟静力法来分析地震边坡的稳定性，由于其概念清晰且计算方便，逐渐成为当前的主流方法。 但是拟静力法忽略了地震的动态过程，因此无法有效反应边坡的永久位移值。NEWMARK[7]1965年提出了计算边坡在动力作用下的滑动位移的方法，并据此得到了边坡的屈服加速度的推导和永久位移分析理论，从而有效分析地震边坡的稳定性。但由于Newmark法的核心为刚性滑块法，忽视了边坡内部变形的影响，此后不断有对Newmark法进行改进的研究[8-10]。

为研究抗拉强度折减对矿山边坡在地震作用下稳定性的影响，本文在前人的基础上，首先通过极限分析上限法对矿山边坡临界的破坏形态以及功能方程进行推导，计算得到不同破坏条件下的边坡屈服加速度的变化趋势，最后针对贺州市某矿山项目中典型矿山边坡，选取实测地震动分析不同参数以及张拉强度折减系数对矿山边坡稳定性的影响。

1 岩土体强度包络线

经典的M-C准则在主应力空间可以表示为一个不规则六边形截面的锥体，如图1所示，当岩体材料以化学键结合时，黏结性表现为单轴抗压强度和单轴抗拉强度。金字塔的顶点表示三轴(各向同性)抗拉强度，而单轴抗拉强度和抗压强度表示为主应力轴与屈服曲面的交点。PAUL[11]对经典的M-C屈服面进行了修改，从而限制了抗拉强度，其屈服面如图2所示。折减后的部分拉力截断单轴抗拉强度ft可表示为图3中的应力圆C1。由图3和图4中的莫尔圆转换至图1和图2中的主应力空间是一个较为复杂的过程，图2中截面ABCDEF上AB边上的应力状态由图4)中的应力圆C2表示，而AB上各个位置由其中主应力的大小确定(σ1≥σ2≥σ3)。例如，图3和图4中的应力圆C1并且σ2=0的情况对应于图2中ABCDEF截面与σ3轴的交点，而图4中点P则与图2中角点C的应力状态相对应。极限状态时的屈服面由图3和图4中光滑的屈服面映射至图1和图2中具有棱角的屈服面。采用此拉应力区的截断方式适用于极限分析中的解析运动学分析方法，但因为主应力空间中屈服面的棱角处的法向量不唯一，其在数值方法中的适用性还需深入研究。传统的M-C强度包络线如图3所示，M-C函数为简单的直线与圆弧部分的组合，在M-C计算中，三轴抗拉强度的大小为：f3t=c/tanφ，而单轴抗拉强度大小为ft=2ccosφ/(1+sinφ)。研究中当考虑抗拉强度的折减时，牵引矢量从直线变化为圆弧，且张拉应力区域的剪胀角δ从φ变化到π/2，当δ=φ时代表线性的M-C屈服准则。为了量化展示折减后抗拉强度，本文引入了抗拉强度折减系数ξ，具体见式(1)。

(1)

(2)

式中，fc=2ccosφ/(1-sinφ)，为单轴抗压强度。

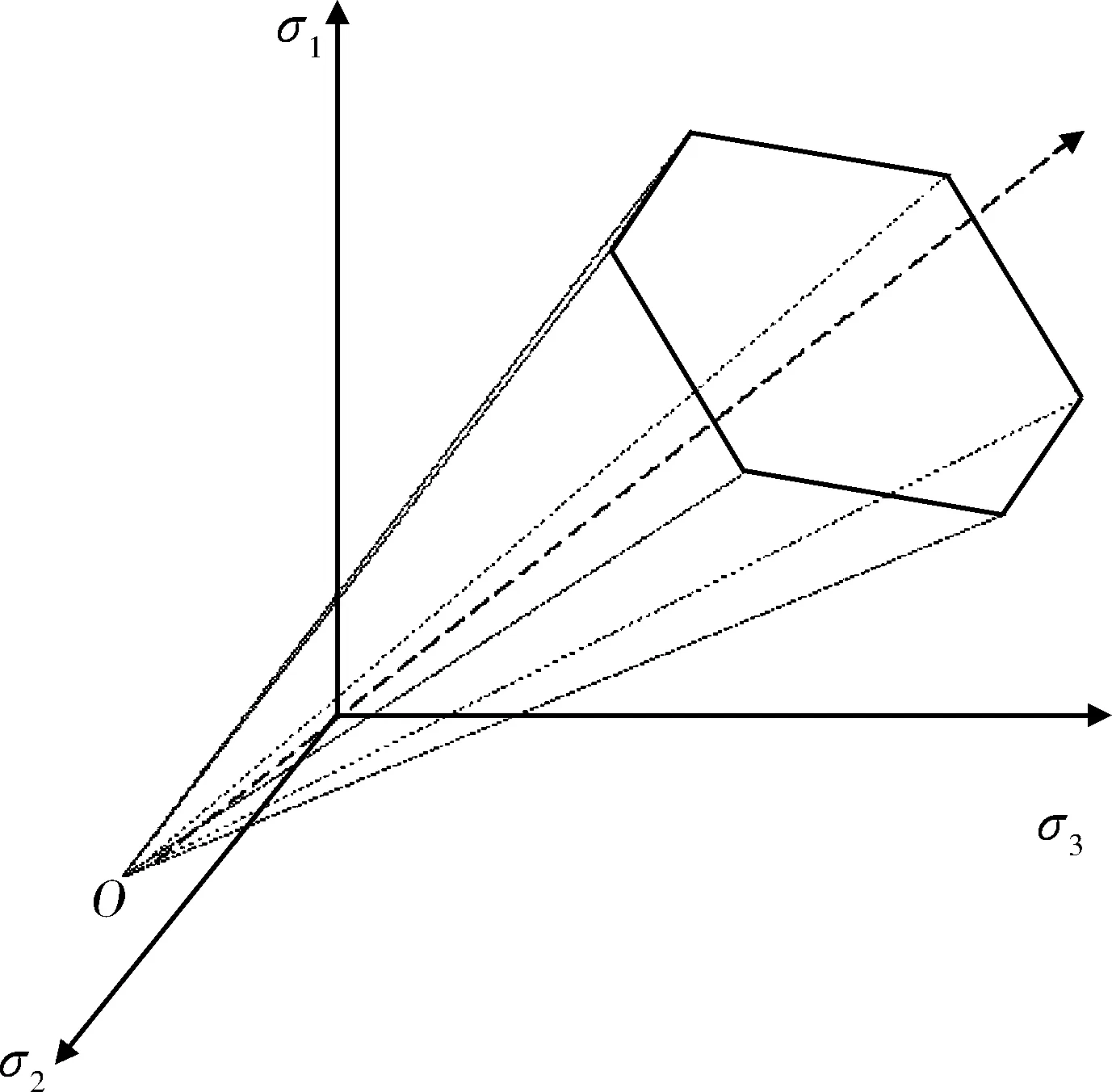
图1 经典M-C屈服Fig.1 The classical M-C criteria

图2 土体受张拉折减屈服Fig.2 Tension cut-off

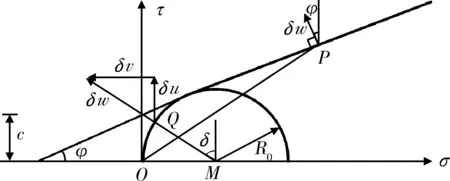
图3 经典M-C包络线Fig.3 The classical M-C envelop

图4 土体受张拉折减包络线Fig.4 Tension cut-off

图5 考虑抗拉强度折减的边坡破坏模式Fig.5 Failure mechanism of tension cut-off slope

2 破坏机制与计算分析

基于极限分析的运动学理论，本文采用张拉剪切破坏机制的对数螺线模式[12]表示边坡的滑动面。图5表示在受地震荷载作用的临界均质矿山边坡模型，其中，β为坡体角度，H为坡体高度；其余参数为内摩擦角φ、黏聚力c和容重γ。边坡的破坏机制如图5所示，块体BDEC以中心O为中心沿着滑裂面DEC旋转，而整个破坏为过破趾的破坏，DEC部分为临界滑面。研究发现，张拉应力更容易出现在坡顶附近，而滑面上部DE部分由受拉伸区折减部分强度包络线而引起，下方较低的部分(EC)是由线性部分的包络线引起。DE部分剪胀角δ从点D的最大值δmax向点E的φ不断折减，见式(3)。

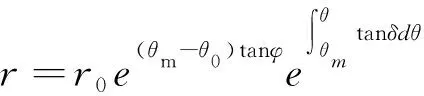
(3)

式中，r0和θ0分别为对数螺旋线起始点A到旋转中心的半径的距离AO和AO与水平参考线的夹角(如图5所示)，其中，θh为对数螺旋线终止点到旋转中心的半径与水平参考线的夹角；θm为OD与水平参考线的夹角；θtc为OE与水平参考线的夹角；δ为剪胀角，其详细的分布形式见式(4)。

(4)

极限分析上限法基于内外能量耗散率的平衡，见式(5)。

Wr+Ws+Wqt=D

(5)

式中：Wr为土体自重状态下的能量耗散率；Ws为拟静力地震荷载作用下的能量耗散率；Wqt为坡顶部荷载的功率；D为滑体BDEC的内能耗散率。外部功率Wr和Ws可表示为块体ABC的功率减去块体ADE的功率，见式(6)。

Wqt=qt×fq

(6)

图5中区域OCA，AOB，BOC，OEA，AOD，DOE的能量耗散功率具体可参考文献[4]，其中：fw与fs均为包含变量：β，θ0，θtc，θm，θh的函数方程。fq计算为式(7)。

(7)

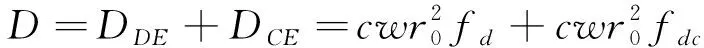
(8)

式中：fd为包含变量θtc，θh，φ的函数，而fdc为包含变量θtc，θm，φ的函数。详细的关于fw，fs，fd，fdc及fq的表达式可参考文献[2]和文献[3]。

将上述公式整理，即可得到屈服加速度Kc，见式(9)。

(9)

式中，Kc为一个含θ0，θtc，θm，θh以及c/γH、坡脚β和内摩擦角φ等参数的函数，则屈服加速度Kc的获取为一系列变量组合下的最小值。即限定条件为式(10)。

0<θ0<θm<θtc<θh<π

(10)

其中，L2/r0，见式(11)。

(11)

本文采用Matlab对上述推导屈服加速度式(10)进行计算，计算时为确保效率快，精度高。采用随机搜索法与序列二次优化结合进行分析。

3 屈服加速度计算

本文针对不同的矿山边坡进行稳定性分析，考虑上部荷载系数qt=0.1～0.3，坡脚β=30°～90°，内摩擦角φ=10°～30°，c/γH=0.10～0.25，以及拉应力区折减系数ξ=0～1的破坏工况。图6～8中上部点线部分表示过坡趾下方的破坏，其余部分线条表示过坡趾的破坏。图6中显示，过坡趾破坏为摩擦体的特征，而当内摩擦角较小时，对于坡脚较为缓和的边坡，则更容易发生过坡趾下方的破坏。但考虑地震荷载影响时，对于内摩擦角更大的边坡易发生过坡趾的破坏。由图6～8可知，考虑张拉区域折减分析，边坡的屈服加速度折减迅速，而针对内摩擦角较小且坡度较大的边坡，破坏更为强烈，而顶部荷载则会加速屈服加速度的折减。

图6 qt=0.1时矿山边坡屈服加速度Fig.6 Yield acceleration of mine slope under qt=0.1

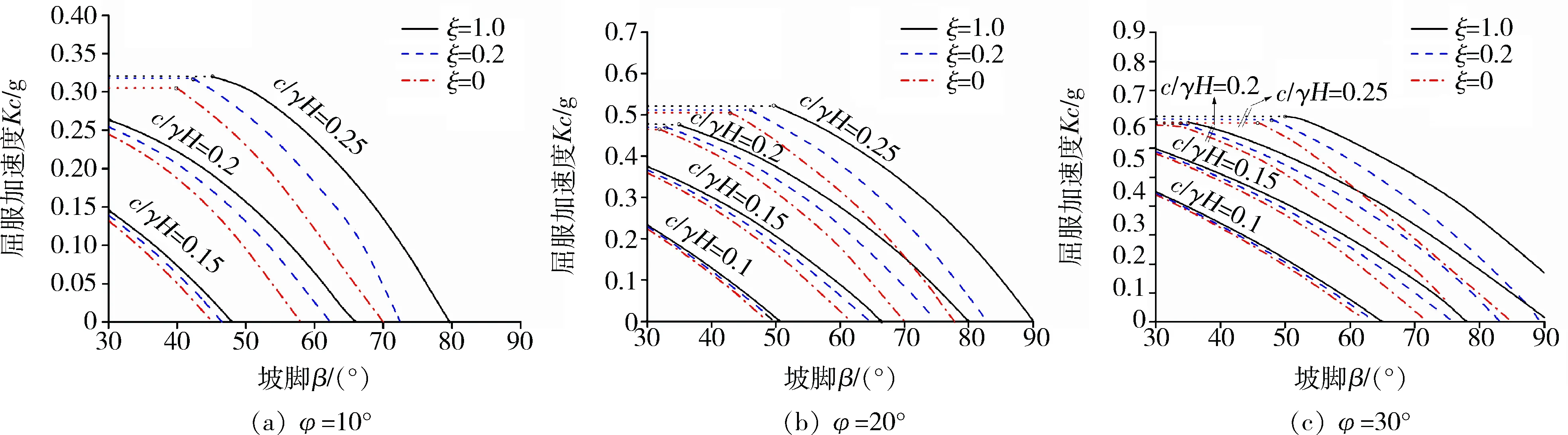
图7 qt=0.2时矿山边坡屈服加速度Fig.7 Yield accelerations of mine slope under qt=0.2

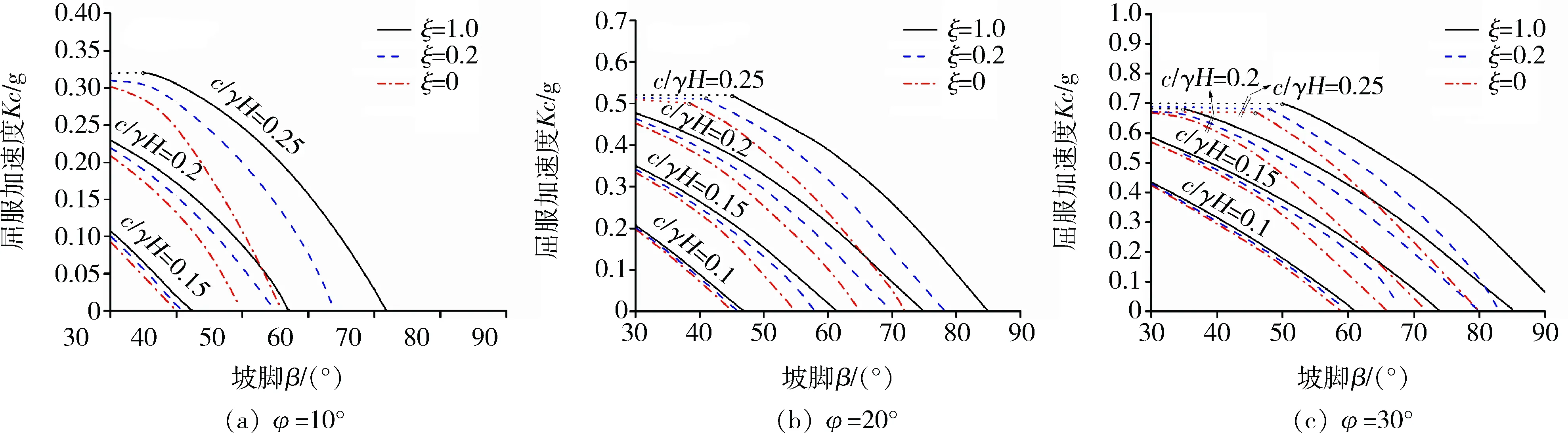
图8 qt=0.3时矿山边坡屈服加速度Fig.8 Yield accelerations of mine slope under qt=0.3

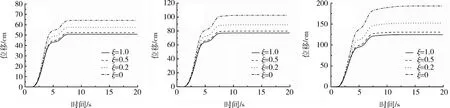
图9 考虑张拉折减下的矿山边坡位移Fig.9 Displacement of mine slope under tension cut-off

4 工程案例分析

在设计中通常采用拟静力来考虑边坡上的地震荷载。为分析地震过程(加速度历史)，对边坡对影响，并深入了解不同顶部荷载系数、张拉区折减系数等因素的影响，本节将针对不同的地震记录得出边坡永久位移的计算结果。

在极限分析上限定理的框架下，CHANG等[13]提出了一种分析具有旋转破坏面的边坡永久位移对方法。本文采用该模型进行分析，永久位移的计算过程简要描述如下：当地震系数K超过屈服加速度Kc时，块体开始滑落。通过平衡功率方程，可获得旋转角加速度，见式(12)。

(12)

式中：G为滑块的重力(即图5中的BDEC部分)；l为滑块旋转中心O到滑块重心的距离。坡脚水平方向永久位移由式(12)的二重积分计算，见式(13)。

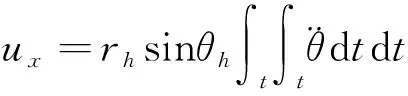
(13)

项目矿山位于广西贺州市八步区里松镇造纸厂东侧约2 km一带的山坡上，隶属贺州市八步区里松镇管辖。矿区距贺州市城区直距约24 km。贺州市城区至里松镇有水泥公路相通，从里松镇到矿区有简易公路相通，路况较差，交通条件一般。

根据现场勘测结果，本文选取代表性的破坏工况为c/γH=0.15，坡脚β=55°，内摩擦角φ=30°。对边坡模型进行稳定性分析。2016年7月31日17时18分，广西梧州市苍梧县发生了5.4级地震，震源深度达到了10 km，本文选取类似地震数据进行输入并深入讨论其在地震力作用下产生的动态永久位移。

图10 考虑张拉区域折减的矿山边坡位移分布Fig.10 Distribution of permanent displacement ofmine slope considering tension cut-off

图9展示了矿山边坡在不同程度张拉折减系数下的永久位移。结果显示，考虑张拉折减的影响，将对边坡永久位移增加将近60%，如针对qt=0.3，边坡在M-C准则与考虑ξ=0时产生的位移分别为123 cm与195 cm，考虑强度折减后永久位移增加了58%。而图10显示，当非线性系数ξ取0.4～1时，非线性准则对于边坡永久位移影响并不明显;而当ξ逼近0时，边坡永久位移产生迅速增加，影响显著。而结果曲率显示，考虑顶部荷载作用对于边坡永久位移的折减程度显著大于无荷载作用边坡。

5 结 论

1) 张拉应力区域折减系数ξ对于屈服加速度Kc的影响显著，考虑坡顶荷载作用则会增加该影响，因此在实践中需要着重考虑边坡后缘拉应力区的影响，并进行适度的加固或减少超载。

2) 永久位移的计算结果显示，考虑张拉折减时，边坡产生的永久位移将达到M-C准则下近两倍，且顶部系数的存在会显著提高张拉强度折减带来的不利影响。