一种波峰波谷检测的智能手机计步算法

毕京学，汪云甲，曹鸿基，齐红霞，姚国标，宁一鹏

（1.山东建筑大学 测绘地理信息学院，济南 250101；2.中国矿业大学 环境与测绘学院，徐州 221116）

室内定位与导航作为位置服务领域的研究热点，受到了公司和机构的大量关注。受室内环境动态多变、结构复杂和成本等因素的影响，单一的室内定位技术难以满足普适、高精度、连续、无缝的定位需求，融合惯性导航的多源混合定位技术成为必然[1-2]，其中，基于智能手机的行人航位推算技术（Pedestrian Dead Reckoning，PDR）是一种低成本、持续性好、广泛应用的室内定位手段[3]。PDR 由步态探测、步长估计和航向估计组成。步态探测通常依据传感器信息的周期性变化识别步数，识别到一步则利用估计的步长和航向推算当前位置，步态探测算法的准确性决定了PDR的优劣，因此，如何利用行人运动特征和传感器信息精确地识别步数成为PDR 的关键。

计步算法主要包括自相关分析法[4-5]、有限状态机法[6-7]、零速检测法[8-9]、谱分析法[10-11]以及波峰检测法[3,12]等。自相关分析法以相关性分析为基础，通过计算两个周期内加速度序列的相关系数以及预设阈值判定有效步数，计步准确率为98%以上[4]，易受干扰动作的影响。有限状态机法将步行过程分为多种状态，通过设定多个阈值实现状态识别与转移实现计步，准确率约为98.8%[7]。零速检测法包含零速修正法和零角速度修正法以及两种方法的组合，通过探测滑动窗口内速度或角速度零值区间识别计步，由于需准确感知零值区间，零速检测法多用于较高精度惯性测量单元（Inertial Measurement Units，IMU），且需要初始对准。谱分析法需将加速度或角速度时域信息转换至频域，根据频域特征完成计步，准确率约为87%[8]和94%[9]。波峰检测法通常利用加速度信号与阈值的关系识别步数，由于算法复杂度低，实现简单，研究成果较多。文献[12-13]分别通过设定不同加速度阈值实现多种运动方式下的精确计步，准确率都在98%以上。文献[14]利用固定时间内加速度和角速度均值自适应设定多个阈值，当多个阈值条件都满足时步数加1，准确率约为98%。现有计步方法对于单一步行活动以及多运动方式尚不能完全准确计步，无法满足更高精度室内定位需求，而且多数方法需设定多个阈值，势必会降低计步方法的准确性和适用性。

针对上述问题，提出了一种移动平均法滤波处理合加速度模值，通过设定波峰和波谷识别条件以及滑动窗口实现计步的波峰波谷检测手机计步算法，在减少阈值个数的同时保证算法准确性和适用性。

1 数据预处理

智能手机内置的IMU 为消费级产品，精度低、噪声多、稳定性差，长时间运行会产生累积误差。考虑到传感器精度和信号稳定性，采用50 Hz 频率获取三轴加速度，并用fs表示。如图1所示为左手/右手打电话时三轴加速度和合加速度模值的变化情况，红、绿、蓝线表示三轴加速度，黑线表示合加速度模值，当分别使用左手和右手打电话时，三轴加速度均有一定程度变化，其中，x轴加速度变化最大，而合加速度模值变化较小。因此，为了减小智能手机在相同活动不同摆放位置或方向下输出三轴加速度对计步算法的影响，采用合加速度模值，计算如式(1)所示，A表示合加速度模值，ax、ay和az表示三轴向加速度。

图1 左/右手打电话时加速度变化情况Fig.1 Change in acceleration when making a left/right call

为了减小传感器噪声对计步算法的影响，考虑到智能手机电量和数据处理能力等方面不足，采用窗口大小为5 的移动平均法对合加速度模值进行滤波处理，如式(2)所示，其中，Ai和Aif分别表示滤波前后的第i个合加速度模值。计算当前时刻的合加速度模值使用了后续两个合加速度模值，使用移动平均法进行滤波处理具有0.04 s 的时间延迟。

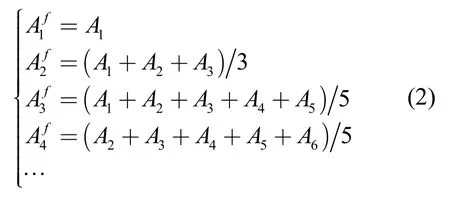
2 波峰波谷检测计步算法

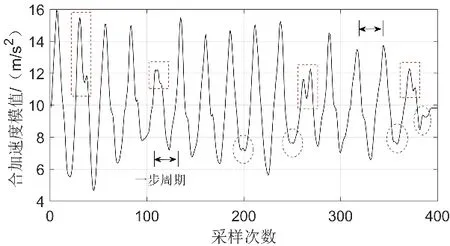
图2 滤波后的合加速度模值变化情况Fig.2 The change of the acceleration modulus after filtering

移动平均法滤波后的合加速度模值变化情况如图2所示，一步周期为迈出一步时合加速度模值从重力加速度大小开始变化至恢复到重力加速度大小的时间，也可以表示两个相邻波峰或波谷之间的时间，红色虚线方框和蓝色虚线椭圆分别标识了不同周期内出现的多个波峰和多个波谷。对于常用的波峰或波谷检测计步算法而言，一步周期内出现多个波峰或多个波谷会干扰步数检测，这些干扰检测的波峰和波谷称为伪波峰和伪波谷。为了消除伪波峰和伪波谷对计步的影响，文献[15]采用巴特沃斯滤波对滤波后的合加速度模值进行再次滤波，虽然效果显著，但波形变化较大，不利于后续行人航位推算。

波峰波谷检测计步算法以滤波后合加速度模值的周期性变化为依据，基于前后两个相邻时刻滤波后合加速度模值识别波峰和波谷，利用识别的首个波峰和波谷以及滑动窗口法完成后续波峰和波谷检测，并通过最小值函数实现步数统计，其原理如图3所示。

图3 波峰波谷检测计步算法流程图Fig.3 The flow diagram of step counting algorithm with peak-valley detection

1）波峰/波谷检测条件

如式(3)所示，当且仅当k时刻的滤波后合加速度模值Akf分别大于k-1 时刻和k+1 时刻的滤波后合加速度模值和时，判定为波峰，波峰次数N+1；当且仅当k时刻的滤波后合加速度模值分别小于k-1 时刻和k+1 时刻的滤波后合加速度模值和时，判定为波谷，波谷次数M+1。

2）首次波峰/波谷检测条件

起始阶段，利用式(4)统计滤波后合加速度模值变大次数tin以及减小次数tde，若，则tin+1；若，则tde+1。

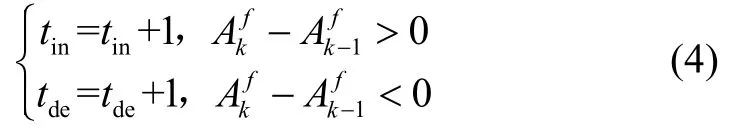
若tin≥5，且tde＜3，同时满足为波峰，则判定为首次波峰，波峰次数N+1，tin和tde重置为0；若tde≥5，且tin＜3，同时满足为波谷，则判定为首次波谷，波谷次数M+1。

3）滑动窗口

对于波峰检测，假设识别的波峰索引为i，则后续w个滤波后合加速度模值（索引为从i+ 1至i+w）不作处理，其中，w为滑动窗口的大小，对应的是滤波后合加速度模值个数；同理，对于波谷检测，假设识别的波谷索引为j，则索引为从j+ 1至j+w的滤波后合加速度模值不作处理。算法从索引为i+w+ 1和j+w+ 1的滤波后合加速度模值开始分别进行波峰与波谷检测，忽略从i+ 1至i+w的滤波后合加速度模值中的峰值以及从j+ 1至j+w的谷值。

4）最小值处理

识别波峰后，波峰次数N+1；识别波谷后，波谷次数M+1。只有一步周期内波峰和波谷都识别后，才能计步，因此，取波峰次数和波谷次数的最小值作为输出步数，如式(5)所示。

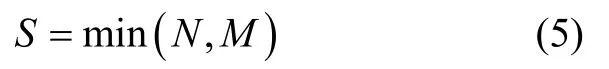
从计步开始到检测到首次波峰，需对滤波后的合加速度模值进行逐个遍历；当检测到首次波峰后，滑动窗口忽略首次波峰后的w个滤波合加速度模值，然后逐个遍历后续滤波后的合加速度模值试图找到后续非首次波峰，即判断索引为i+Sw+ 1的滤波合加速度模值是否大于和，若非波峰，则继续判断是否大于前后2 个相邻时刻的滤波合加速度模值和，直至检测到另一个非首次波峰，然后再滑动窗口重复上述过程。同理，波谷检测也是如此。

提出的波峰波谷检测计步算法仅利用前后两个相邻合加速度模值的大小关系识别波峰和波谷，没有使用合加速度模值经验阈值，唯一的参数为滑动窗口大小w。w取值是否合理在一定程度上影响计步算法的准确性，若w设置过大，则无法及时识别一步，且容易忽略部分步数；若w设置过小，将会增加算法的时间复杂度且识别到更多步数，过大或过小的w都将影响计步准确性。

3 实验与分析

图4 试验场及实验路线Fig.4 The testing ground and test route

图4为中国矿业大学室内定位试验场示意图，实验路线为4 段走廊，总长约211 m，由2 名实验人员沿实验路线分别平端智能手机步行2 次完成数据采集。实验人员为男女各1 名，身高分别为1.77 m 和1.58 m。智能手机型号为小米6，三轴加速度的采样频率为50 Hz。采集过程连续，在走廊拐弯处无停留。同时，男性实验人员以正常步速分别按照发短信、打电话、和摆臂活动以及智能手机在裤子口袋各采集20步数据，实验过程中，智能手机与动作同步。行走的真实步数由实验人员统计得到。

3.1 滤波处理实验及分析

选取7 步周期共计193 个合加速度模值进行滤波处理，结果如图5所示，黑线表示原始合加速度模值，绿线、蓝线和红线分别表示采用移动平均法、移动平均法加卡尔曼滤波[15]和巴特沃斯滤波加移动平均法[16]滤波后的合加速度模值。黑线所示的原始合加速度模值在同一步态周期内存在多个波峰或波谷，三种滤波方法都可以消除黑线中多余的波峰或波谷。从平滑效果来看，巴特沃斯滤波加移动平均法的平滑效果最优，移动平均法次之，移动平均法加卡尔曼滤波仍含有伪波峰，效果较差。巴特沃斯滤波可通过设定通带和阻带频率更好地滤除噪声，因而具有最佳平滑效果。

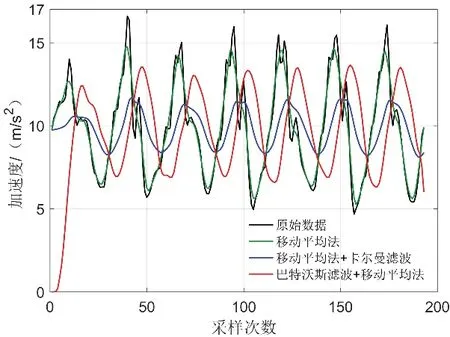
图5 滤波效果Fig.5 Filtering effect

从波形变化方面来看，采用卡尔曼滤波和巴特沃斯滤波后的合加速度模值波形都存在较大变形和偏移。卡尔曼滤波后的合加速度模值波形变化较大，波峰位置发生较大右偏移；由于起始阶段数据量不足，巴特沃斯滤波后的合加速度模值波形在起始阶段由0不断增大，波形变化程度小于卡尔曼滤波，波峰位置右偏移大于卡尔曼滤波；移动平均法的波形变化最小，波峰位置与滤波前基本一致。波峰位置右偏移表示波峰检测存在时间延迟，虽然不影响计步精度，但是一步周期会发生变化。

如表1所示为三种滤波方法处理193 个合加速度模值消耗时间统计，在仿真平台相同的情况下，移动平均法消耗时间为2.55×10-4s，而移动平均法加卡尔曼滤波以及巴特沃斯滤波加移动平均法的消耗时间分别约为移动平均法的3.1 倍和29.2 倍。仿真平台为Matlab R2016a 64 位，处理器型号为i7-9700 k，主频为3.6 GHz。尽管智能手机的数据处理能力有较大提升，但是相较于计算机还有较大差距，在进行滤波处理时智能手机消耗时间可能更长。

表1 三种滤波方法的消耗时间统计Tab.1 Consumption time statistics of three filtering methods

综合考虑平滑效果、波形变化、消耗时间以及智能手机数据处理能力和电量水平，进行滤波处理时不建议采用多级滤波的方式，而是简单且效果较好的移动平均法滤除合加速度模值中的伪波峰和伪波谷。

3.2 步数检测实验及分析

3.2.1 平端智能手机步行实验

如表2所示为基于2 名实验人员的4 次实验数据分别采用自相关分析法[4]、加速度差分有限状态机法[7]（AD-FSM）、固定阈值波峰检测法、传统波峰检测法和本文提出的算法识别步数统计。从表中可以看出:

1）由于传统波峰检测法将识别到的所有波峰都用于步数统计，而采用移动平均法滤波处理后的合加速度模值存在很多伪波峰，识别的步数大于实际步数，计步精度不高，平均计步准确率为61.85%；

2）当阈值设为12 m/s2时，固定阈值波峰检测法具有最高精度，平均计步准确率为99.16%，当阈值设为较大值时，识别步数小于实际步数，当阈值设为较小值时，识别步数大于实际步数；

3）AD-FSM 法的平均计步准确率为98.99%，平均错误识别步数为3 步，该方法借助加速度差分和多个次数阈值实现计步，当一步周期内滤波后合加速度模值含有较多伪波峰时容易导致步数错误估计；

4）自相关分析法的平均计步准确率为98.57%，平均错误识别步数为4～5 步，该方法通过相邻2 个周期的相关性及相关系数阈值识别步数，当第2 个周期内步速、步行方式或方向发生变化时会出现不满足阈值条件的情形，导致步数错误估计，譬如:实验过程中的拐弯；

5）本文所提出的算法在2 名实验室人员不同步速下的计步准确率都为100%，相比于常用算法提高了1.01%～38.15%。

表2 多种计步算法识别步数统计Tab.2 Step detection statistics of several step counting algorithms

如图6所示为采用本文提出的计步算法开展第1次和第4 次步数检测实验计步准确率随着窗口大小w的变化情况，蓝色星形线表示第1 次实验，黑色十字线表示第4 次实验，两次实验的计步准确率都随着w的增大而由小变大然后变小，充分说明了w对计步准确性的影响，w过大或过小都将产生步数错误估计。第1 次实验中w取值为13～20 时计步准确率为100%，而第4 次实验中w取值为16～21 时计步准确率为100%，由此可知，当窗口大小w取值为16～20 时可保证2 名实验人员100%计步准确。但是，为了让所提计步算法更具普适性，建议将窗口大小w设为16。

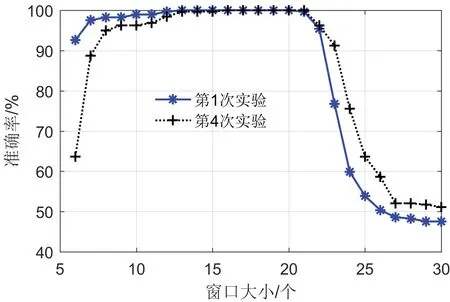
图6 计步准确率与窗口大小的关系Fig.6 The relationship between step counting accuracy rate and window size

图7为利用所提出的算法识别波峰和波谷的情况，数据为第1 次实验滤波后的合加速度模值并用蓝色实线表示，红色星形表示波峰，黑色圆圈表示波谷，从图中可以看出，所提出的算法可以准确识别波峰和波谷位置，换言之，该算法能够准确识别步数。

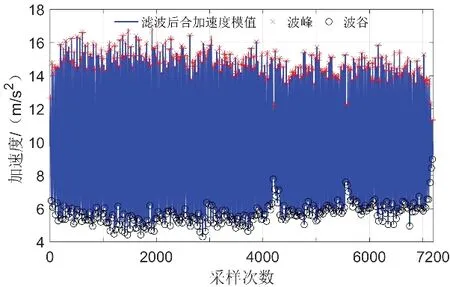
图7 识别的波峰和波谷Fig.7 The detected peaks and valleys

如表3所示为多种计步算法基于第1 次实验滤波后合加速度模值的消耗时间统计，仿真平台和处理器与3.1 节相同。从表中可以看出，AD-FSM 法消耗时间最短，传统波峰检测法消耗时间次之，固定阈值波峰检测法和本文所提出算法的消耗时间较短且非常接近，自相关分析法消耗时间最长，约为本文所提出算法的11.4 倍。由于自相关分析法[4]可以在手机上运行，本文提出的波峰波谷检测计步算法能够在现有智能手机上流畅运行。

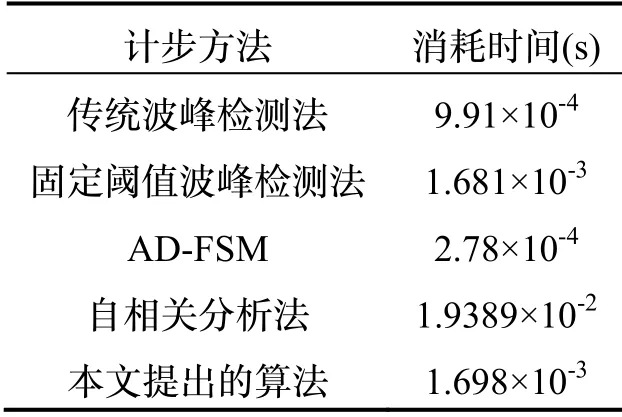
表3 多种计步算法消耗时间Tab.3 Consumption time of several step counting algorithms

3.2.2 多种活动步行实验

如图8所示，发信息、打电话、摆动、在裤子口袋中加速度变化趋势各不相同，摆动和口袋时的合加速度模值波动频繁且数值较大，传统波峰检测法和固定阈值波峰检测法精度相对较低，因而，选择AD-FSM和自相关分析法与本文所提出算法进行比较。

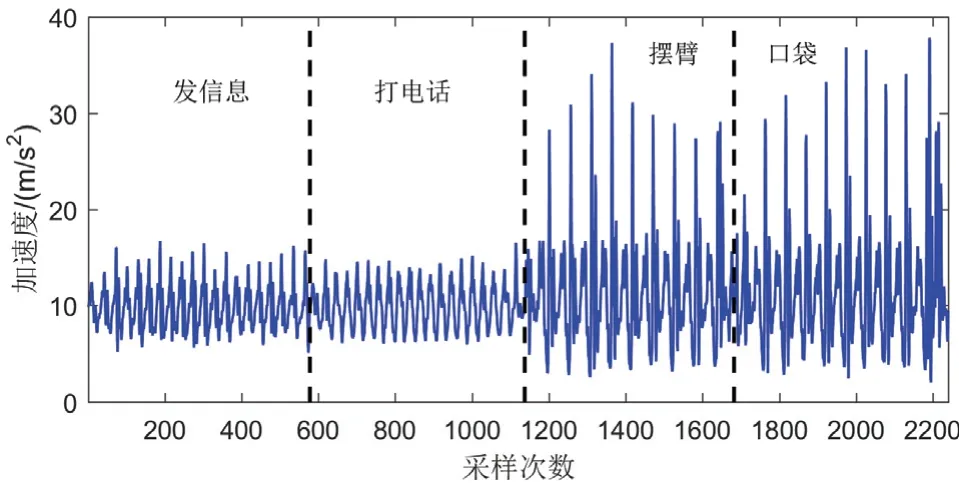
图8 多活动下的加速度变化情况Fig.8 Acceleration modulus changes under several activities

表4为多种活动下各计步算法识别步数统计。发信息和打电话时，各计步算法都有较高精度，AD-FSM、自相关分析和所提出算法的错误识别步数分别为1、2 和0 步，提出算法的准确率为100%，自相关分析法的准确率最低，为95%；摆臂时，所提出算法错误识别步数为0 步，准确率为100%，AD-FSM的错误识别步数高达9 步，准确率仅为55%，准确率远低于自相关分析和提出算法；智能手机放在裤子口袋时，AD-FSM、自相关分析和提出算法的错误识别步数分别为5、2 和1 步，所提出算法的准确率为95%，AD-FSM 的准确率最低，为75%；在多种活动下，AD-FSM、自相关分析和所提出算法的总体错误步数分别为16、8 和1 步，对应的准确率分别为80%、90%和98.75%。总体而言，在多种活动下，相比于AD-FSM和自相关分析法，提出算法的准确率提高了8.75%～18.75%。

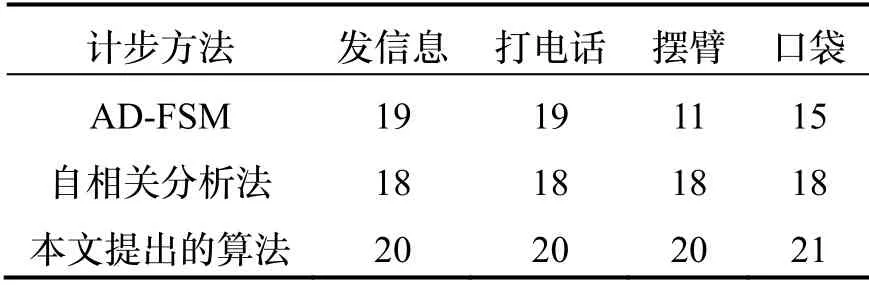
表4 多活动下各计步算法识别步数Tab.4 Step detection statistics of several step counting algorithms under several activities

4 结 论

本文提出了一种适用于智能手机的波峰波谷检测计步算法，实验结果表明该算法对于平端活动下不同行人和不同步速可以实现100% 准确计步，对于多种活动正常步行可以实现98.75%准确计步，具体结论如下:

1）针对智能手机采用何种滤波方法处理加速度的问题，从平滑效果、波形变化和消耗时间方面对比分析了三种滤波方法，考虑到智能手机数据处理能力和电量水平，应当选择简单且效果较好的滤波方法，如移动平均法，而非多级滤波或高级滤波的方式。

2）针对现有计步算法对于不同行人、步速和活动存在步数错误估计的问题，提出了利用波峰检测、波谷检测和滑动窗口法的计步算法，由2 名实验人员在211 米走廊内平端智能手机开展步行实验的计步准确率都为100%，与常用计步算法相比，精度至少提高了1.01%；对于多种活动步行而言，所提出算法的计步准确率为98.75%，与常用计步算法相比，精度至少提高了8.75%。

3）在相同仿真条件下，所提出算法的消耗时间仅为自相关分析法的8.7%，能够在智能手机上流畅运行。

在后续研究中，将增加测试人员、测试场景和实验路线，融合多源传感器数据，结合机器学习算法，研究面向智能手机的多活动高精度计步算法以及行人航位推算方法。