基于PolyMax模态参数识别法的轴装式制动盘模态试验
2020-10-17焦标强曹建行吕宝佳张化谦宋跃超陈德峰
焦标强,曹建行,吕宝佳,张化谦,宋跃超,陈德峰
(1.北京纵横机电科技有限公司,北京 100094;2.中国铁道科学研究院 研究生部,北京 100081)
模态参数识别技术在工程结构的健康监测、日常维护和振动控制等方面,有重要的科学研究和实际应用价值[1]。任何结构都能被简化为“弹簧—质量—阻尼”系统,结构损失将引起模态参数的变化[2]。因此,结构模态参数变化标志着结构发生了损伤[3],能够用来表征结构的实际运行工况和真实的动力学特性。模态分析是求解物理空间中复杂耦合运动方程特征值,并将其转化为1组解耦的单自由度运动方程,是研究结构动态特性、避免发生共振、提高工作稳定性的重要方法[4-5]。
制动盘作为高速列车制动系统的关键核心部件之一,其振动特性直接影响整车运行安全和运营成本,深入研究制动盘动力学特性对列车的稳定安全运营具有重要科学参考价值[6-7]。然而,轴装式制动盘盘体具有多个小圆柱腹板,盘毂上具有锥形空洞,因其结构复杂不易通过有限元法获得精确地模态参数,相比之下试验方法更能精确地获取其模态参数。根据信号域的不同,结构模态参数识别方法主要有频域法[8]、时域法[9]和时频域法。频域法通过结构传递函数或频响函数(FRF)进行模态识别;时域法是直接利用实测信号建模进行模态识别,一定程度上弥补了频域法的不足;时频域法在非线性非稳定信号的模态识别方面具有一定优势,但在实际工程中能够应用的时频域法较少。Poly-Max模态参数识别法属于频域法,采用离散时间频域模型,能够较好解决频域法中的数值病态问题,既适用于弱阻尼数据,也适用于强阻尼数据,能够得到清晰易分离的稳态图。
本文基于PolyMax模态参数识别法,对轴装式制动盘进行模态参数识别试验,研究制动盘的主要振动形式,分析制动盘动态特性,探究了附加质量对制动盘模态频率的影响,为进一步优化设计制动盘的动力学提供理论参考。
1 PolyMax法模态参数识别原理
PolyMax模态参数识别法是集最小二乘复频域法(LSCF)和最小二乘复指数法(LSCE)各自的优点,得到清晰易分离的稳态图,通过稳态图对极点和结构模态参与因子进行整体估计,获得制动盘结构振动模态频率、阻尼和模态参与因子,进而将非线性目标函数线性化处理得到频响函数参数矩阵的线性矩阵分布模型,求解基于压缩正则方程的最小二乘问题得到相关模态参数[10-11]。针对高度密集模态和FRF数据被噪声污染等问题,PolyMax模态参数识别法仍能获得清晰的稳态图,精确地识别每一阶模态参数[12]。频域中系统的输出和输入关系可用右矩阵分式模型来描述,其数学模型为

其中,
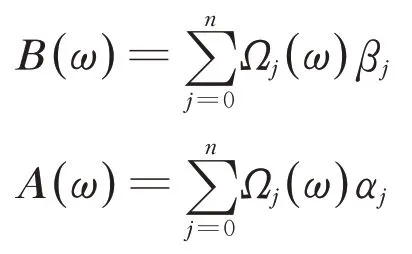
式中:ω为角频率;H(ω)为制动盘系统理论频响函数矩阵;B(ω)为输出参数矩阵;A(ω)为输入参数矩阵;Ωj(ω)为基函数;n为多项式阶次;βj和αj(j=0,1,…,n)分别为分子和分母多项式系数。
加权线性最小二乘估计的标准方程为
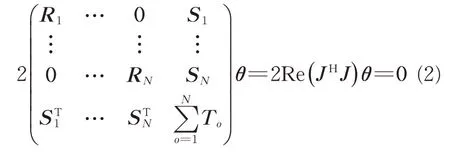
其中,
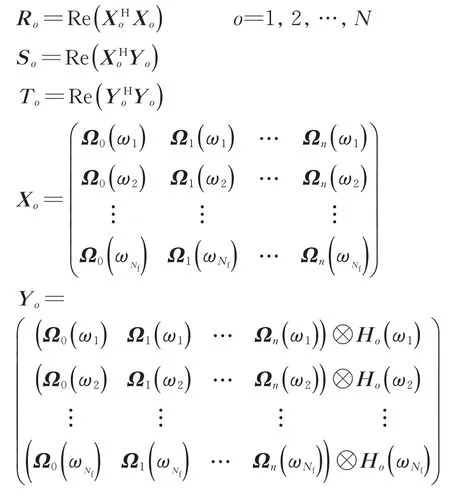
式中:0 为零矩阵;J为雅可比(Jacobian)矩阵;θ为参数矩阵;(·)H为矩阵的厄米特共轭矩阵;⊗为克罗内克(Kronecker)积;Nf为识别频段内包含的谱线数;Ho(·)实测频响矩阵的第o行;N为输出参数最大通道数。
考虑标准方程结构特性下,根据线性方程组求解理论,求得分母系数矩阵α及其伴随矩阵的特征值和特征向量,这样就可得到系统极点和相应模态参与因子,其方程为
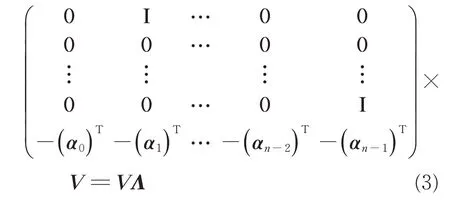
式中:I 为单位矩阵;V为特征向量矩阵;Λ为酉矩阵的特征值矩阵。
对角元素Λik与系统极点pi和pi*间存在以下关系。

其中,
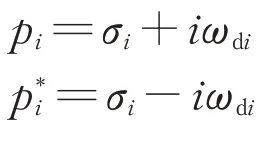
式中:i为阶数;Ts为采样时间;σi为阻尼因子;ωdi为有阻尼固有频率。由式(4)可解得
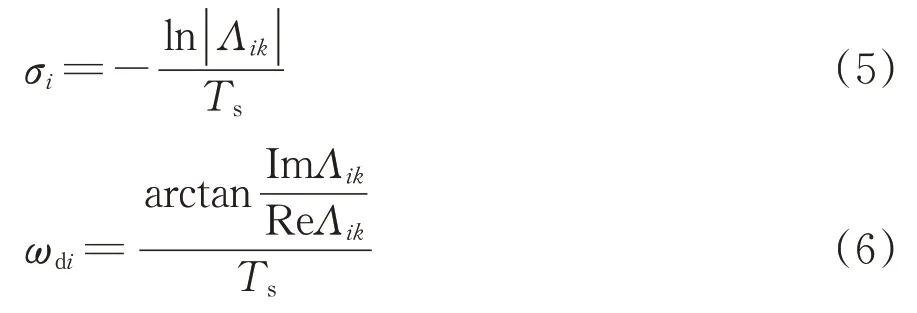
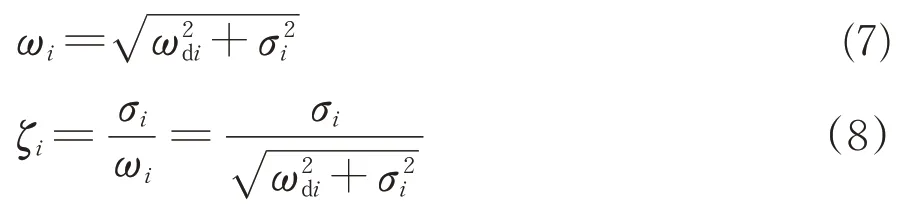
由此可解得频率ωi和阻尼比ζi为式中:ωi为第i阶无阻尼固有频率;ζi为阻尼比。
2 制动盘模态试验
2.1 试验对象及设备
轴装式制动盘主要由盘体、盘毂、挡块、压环、连接螺栓、防松螺母和油堵组成。采用LMS多功能数据采集器(SCADAS)进行信号采集、LMS TestLab 软件进行数据分析,传感器为B&K单向压电式加速度传感器(4个),力锤为PCB型。
2.2 测量方案
2.2.1 测量系统
测量系统是整个动态测试系统的关键环节,直接关系试验的成败和精度。测量系统主要由激励装置、传感器及数据采集系统组成。通常情况下选择测量系统时要考虑试验要求的幅值量级、频率范围和测量参数以及试验环境等诸多因素。制动盘模态试验测量系统如图1所示。
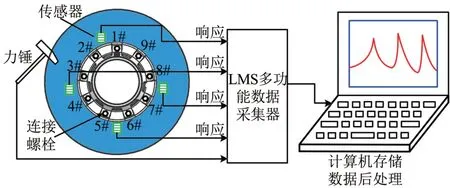
图1 制动盘模态试验测量系统
2.2.2 激励点和测量点布置
制动盘是典型的循环对称结构,采用柱坐标建模方式建立轴装式制动盘几何模型。综合考虑模态测点覆盖整个制动盘和激励点数量,布置激励点时沿径向方向将制动盘划分为4等份,即在制动盘面上2 圈、轮毂1 圈、挡圈1 圈,共4 圈位置上均匀布置激励点,共有36个激励点,如图2(a)所示,图中红色圆点代表激励点位置。
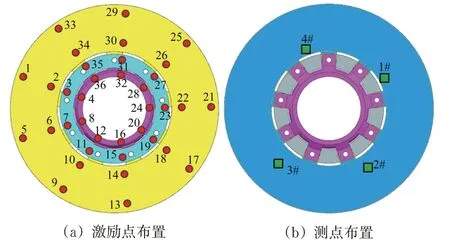
图2 激励点和测量点布置
为提取到制动盘的重根模态,试验时采用了多激励点方式,4 个加速度传感器分别安装在激励点2,点10,点18 和点30 的背面,如图2(b)所示,图中绿色方块代表传感器位置。
试验中,采用传感器固定、力锤移动的方式进行。分析频率为4 096 Hz,力锤锤头选用尼龙头。锤击测试时,采样点数为4 096个。
2.2.3 试验步骤
1)建立几何模型
试验前在软件LMS Test Lab 软件中建立制动盘简易几何模型,按照试验时布置的36 个激励点和4个测量点,用粉笔在制动盘表面标记出36个激励点和4个测量点,所建几何模型和试验装置如图3所示。
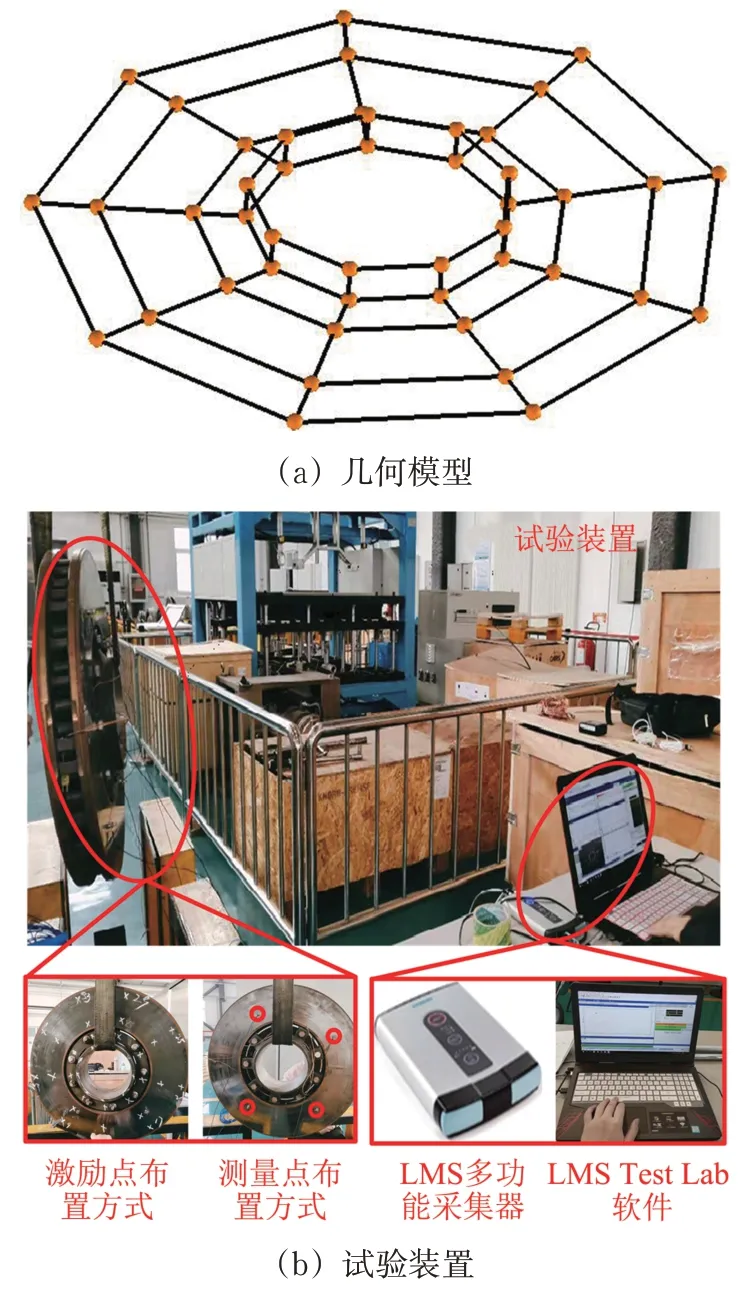
图3 制动盘几何模型和试验装置
2)数据采集
试验时采用弹性绳将制动盘悬挂,使其处于自由状态,将力锤和加速度传感器与LMS 多功能数据采集器对应通道连接好,采用磁力座吸附方式将加速度传感器吸附在制动盘标记点表面。
3)参数识别
将采集到的各激励点数据输入到LMS Test lab软件的模态分析模块中进行参数识别,选择恰当地分析频段得到各测量点的频响函数和相关函数曲线。
3 制动盘模态分析结果
试验选用的单向B&K 型加速度传感器,质量为2.9 g,为评价传感器附加质量对制动盘模态频率的影响,下文分2 步进行分析。第一步,仅安装1 个传感器测量得到频响函数曲线;第二步,在第1 个传感器上再安装1 个同型号传感器,仅用于增加附加质量,测量传感器仍用第1 个传感器。2 次测量获得的频响函数曲线如图4所示。从图4可以看出:2 次测量获得的频响函数完全重合,这一结果表明传感器附加质量对制动盘结构的整体模态频率无影响。
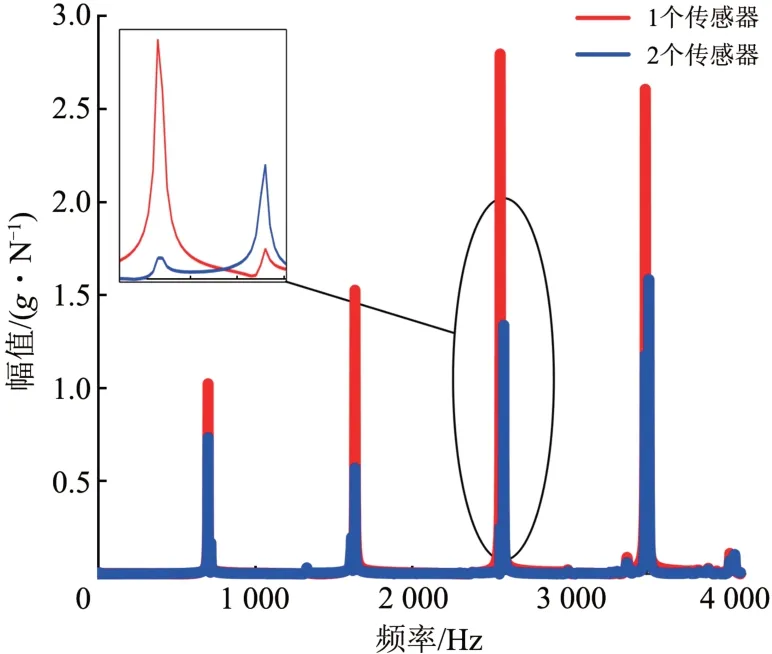
图4 附加质量对频响函数的影响
试验中当力锤产生的脉冲达到触发水平时,数据采集器同时采集4 个传感器的振动加速度信号,每个测量点进行3次敲击,采用谱平均法得到不同激励点的频响函数曲线。这些频响函数曲线变化规律相同,随机列出10#测量点的频响函数曲线如图5所示。
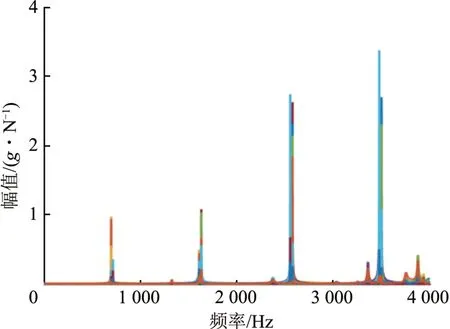
图5 10#测量点频响函数曲线
对36 个激励点,分别进行锤击实验采集各点振动信号,通过采集制动盘振动信号,根据式(1)计算得到制动盘频响函数曲线,然后采用PolyMax 模态参数识别法,根据式(3)和式(4)计算获得极点与参与因子,进而根据式(7)和式(8)提取制动盘模态参数,建立稳态图如图6所示,制动盘前10 阶固有频率和阻尼见表1,前10阶模态振型如图7所示。表1中,模态振型(m,n)表示振型中含有m个节圆和n个节径。
综合表1、图5—图7可知:制动盘振动模态有周向模态、径向模态和混合模态,在频率1 627 Hz附近存在频率几乎一致的重根模态;制动盘模态复杂性比较小,近似为实模态振型,满足循环对称结构的典型模态振型特征。
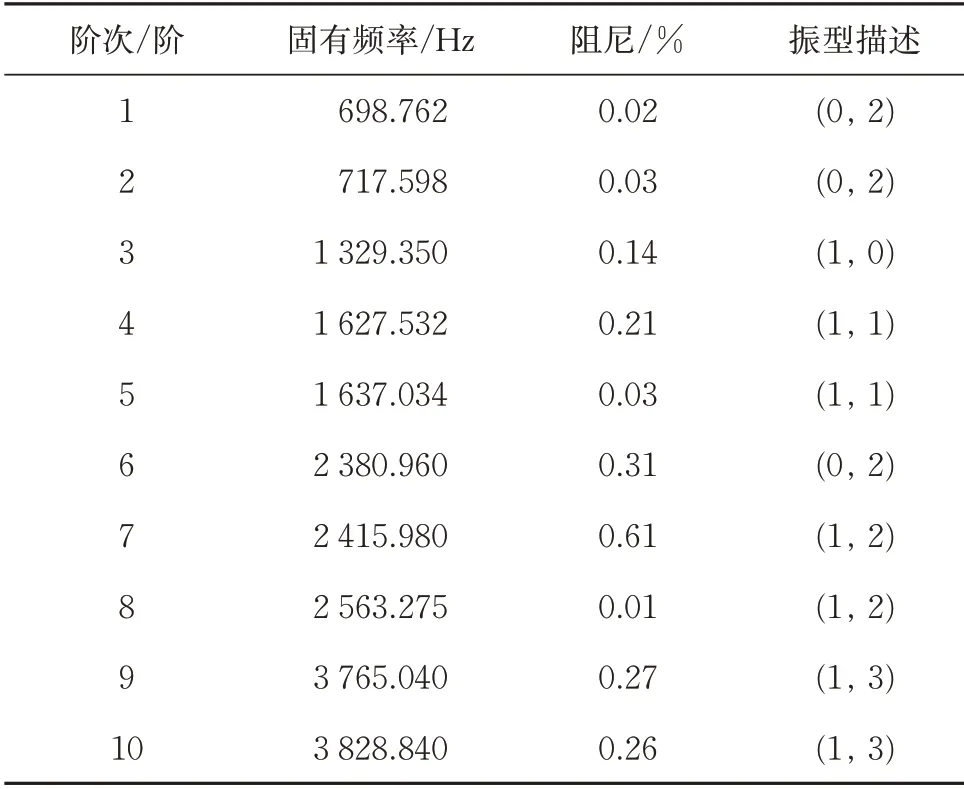
表1 制动盘模态参数
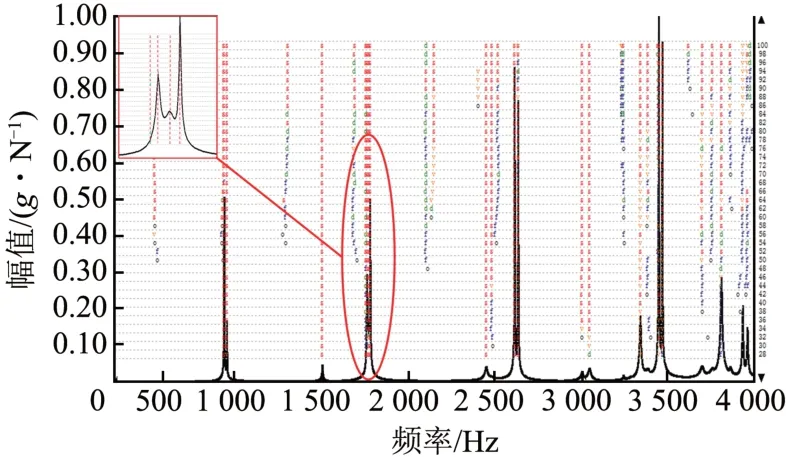
图6 稳态结果

图7 制动盘模态振型
将模态振型映射为Hilbert 空间中的向量,用振型向量间的点积即模态判定准则(Auto MAC)表征2 个模态振型向量几何上的相关性[13]。Auto MAC值接近0,表明2个振型向量间相关性很小或正交;Auto MAC 值接近1,表明2 个振型向量间彼此平行或相关性很大。
基于PolyMax模态参数识别法获得的制动盘模态Auto MAC 值如图8所示。由图8可以看出,非对角线的Auto MAC 值接近于0,对角线的Auto MAC值为1,这一结果表明制动盘不同阶次振型相关性很小,无虚假模态存在,振型结果准确可靠。
4 结 论
(1)分析传感器附加质量对制动盘模态频率的影响,结果表明传感器附加质量对制动盘结构各阶模态频率无影响。
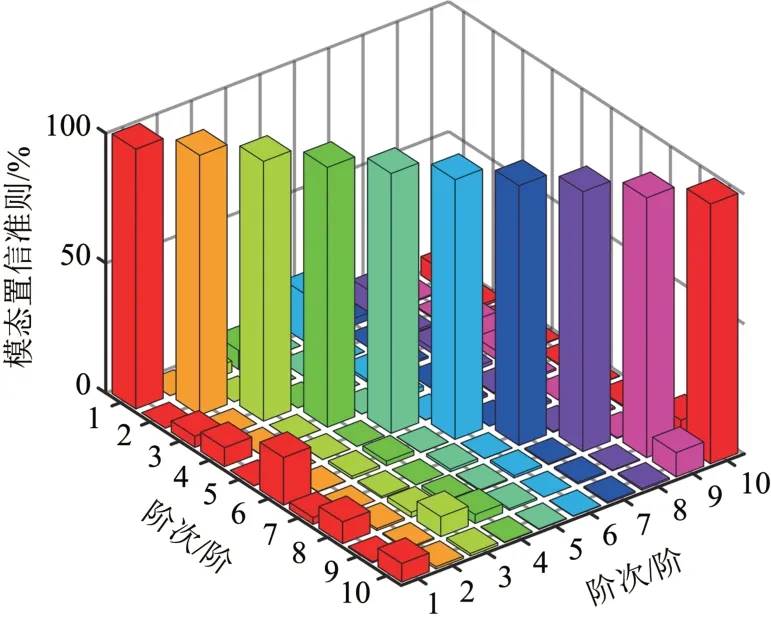
图8 模态判定准则结果
(2)基于PolyMax模态参数识别法计算轴装式制动盘模态,得到制动盘前10 阶固有频率、阻尼和振型。结果表明制动盘的模态振型主要有周向模态、径向模态和混合模态3种。制动盘为循环对称结构,存在大量的重根模态。
(3)相较于有限元法,对于复杂结构采用PolyMax 模态参数识别法能更准确地识别模态参数,为制动盘结构的动力学研究奠定了基础,同时也为工程应用提供了理论指导。
