高速铁路跨地裂缝带双线路基动力响应
2020-10-17黄强兵薛力铭何国辉
黄强兵,薛力铭,何国辉,王 涛
(1.长安大学 地质工程系,陕西 西安 710054;2.长安大学 西部矿产资源与地质工程教育部重点实验室,陕西 西安 710054)
我国高速铁路建设常常会遇到诸如地裂缝[1-2]、地面沉降[3-4]、岩溶[5]和冻土[6]等特殊地质问题,给我国大规模的高铁建设带来了潜在安全隐患。地裂缝在我国较为发育,分布范围广,其中华北平原、汾渭盆地和苏锡常地区最为典型[7]。我国多条高速铁路穿越这些地裂缝发育区,地裂缝为一地层软弱带或裂隙带,受构造运动或下伏基岩的控制,地下水开采(抽水)可能会导致其活动,引起地层错动和地表差异沉降,在列车振动荷载作用下地裂缝场地的动力响应对高速铁路路基稳定性及安全运营构成了威胁。开展跨地裂缝带路基动力响应研究,对于我国当前如火如荼的高铁工程建设及病害防治具有十分重要的意义。
国内学者从理论解析、数值模拟、模型试验和现场测试角度对列车荷载作用下路基动力响应开展了大量研究,取得了很多重要成果。如Krylov[8]采用格林函数法研究了列车速度对地面动力响应的影响,Hung 等[9]用亥姆霍兹势和傅里叶变换方法研究了黏弹性地基在动力荷载作用下的动力响应。Jiang 等[10]建立了全比尺室内无砟轨道高铁路基模型,研究了路基在不同速度、荷载和水位下的动力响应。Momoya 等[11]开展了缩尺比例为1∶5的有砟轨道路基低速模型试验,研究了移动荷载作用下铁路路基变形特性。Madshus 等[12]在软土地基上完成了挪威—瑞典高速铁路的试验,提出了路基振动模型。EI Kacimi等[13]考虑材料阻尼和材料非线性,建立了车辆与多层土耦合的三维有限元模型,研究了列车通过时的频率效应对亚临界列车速度下轨道动态响应的影响。Varandas 等[14]通过三维模拟分析了过渡区压载层和路堤沉降增加的原因。总体上来讲,对单线铁路路基动力响应研究较多,而对双线铁路对向行车条件下动力响应的研究较少[15],跨越地裂缝带高铁路基动力响应研究鲜有文献报道。
本文以大西客运专线高速铁路跨山西太原盆地祁县东观变电站地裂缝带为工程背景,采用Midas/GTS 大型有限元分析软件,建立地裂缝带—路基—天然地基三维动力有限元计算模型,进行单线和双线对向行车条件下跨地裂缝带的双线路基垂向动力响应以及对向行车条件下不同行车速度对地裂缝带上、下盘路基垂向动力响应的影响规律研究,研究结果可为地裂缝带发育区高速铁路工程建设及病害防控提供科学指导。
1 工程背景
大西客运专线是中国“八纵八横”客运专线网中的京昆通道的重要组成部分。它东起山西大同,西至陕西西安,线路全长859 km,设计行车速度250 km·h-1,在穿越太原、临汾及运城等盆地地区时沿线具有一定规模的地裂缝带达21 条之多,与大西客运专线线路相交36 处,且活动强烈,其中太原盆地东观变电站地裂缝带(TY3)活动最为典型。
东观变电站地裂缝带(TY3)位于山西太原盆地祁县,从太谷县武家堡村南向西南方向延伸,经祁县张家堡、乔家堡北等地,由主裂缝(TY3)和次级裂缝(TY3’)组成,地表出露明显,呈带状或串珠状。主地裂缝带(TY3)总体走向为73°,倾向163°,倾角80°,长约10.2 km,缝宽0.2~1.0 m,其活动以垂直位错为主兼有水平拉张(图1(a)),以祁县东观变电站附近活动最明显。次级裂缝(TY3’)与线路相交段的裂缝走向为76°,地表表现为串珠状陷穴(图1(b))。本研究取东观变电站地裂缝带为依托工点,简化地层剖面及地下水位如图2所示。其地层主要物理力学参数见表1。

图1 东观变电站西地裂缝带(TY3)地表出露情况
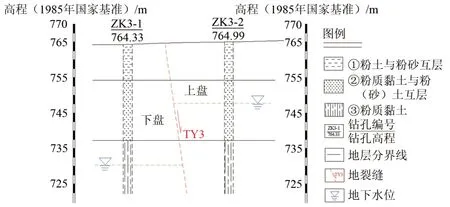
图2 东观变电站地裂缝带(TY3)地层剖面图
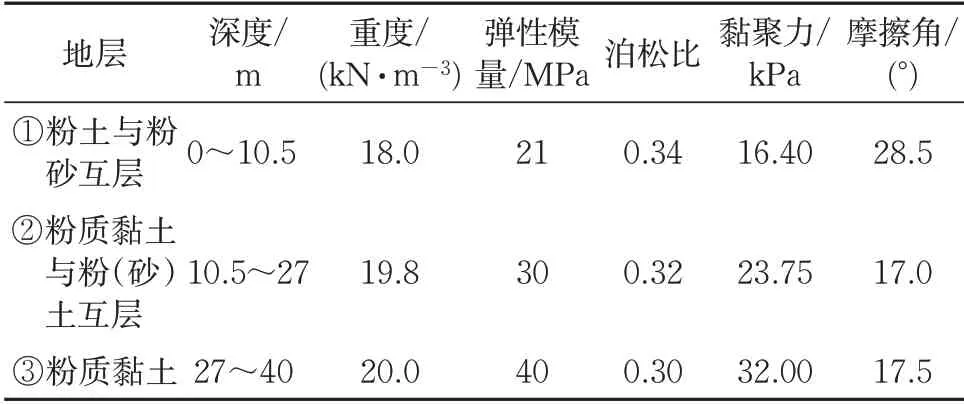
表1 地层物理力学参数
2 地裂缝带—路基—天然地基动力有限元模型
为研究跨地裂缝带高铁双线路基动力响应,采用Midas/GTS 大型有限元分析软件,建立地裂缝带—双线路基—天然地基三维动力有限元计算模型,如图3所示。模型纵向长度取100.0 m,宽取85.0 m,地层厚度取40.0 m,路基高为5 m。地裂缝带倾角取80°,其走向与路基正交。轨道系统由钢轨、扣件、轨道板构成,铺设在路基上,路基系统从上到下依次为基床表层、基床底层、路基本体以及地基,双线间距为4.6 m[16]。由于本文主要研究跨地裂缝带路基结构的动力响应,为了提高计算精度,路基及地基上部网格区域加密,整个模型单元数目243 412 个,节点数目194 706 个。
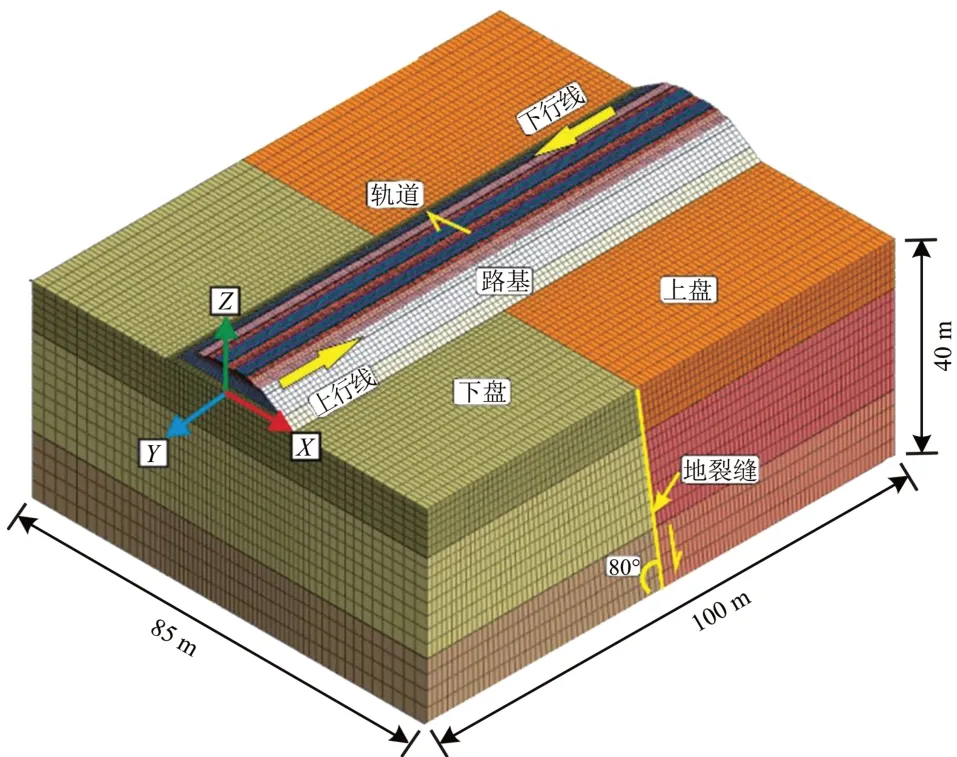
图3 动力有限元计算模型
计算模型主要包括双线路基模型、地裂缝带接触模型、阻尼边界设置等方面。其中钢轨、轨枕采用线弹性材料模型,扣件采用弹簧阻尼单元模拟,刚度取80 kN·mm-1,阻尼系数为30 kN·(m·s)-1,路基各结构层均采用摩尔—库伦塑性材料模型,各结构及地层材料的物理力学参数见表2。地裂缝带采用有限元中的Goodman接触单元实现,法向刚度取10 MPa,切向刚度取1 MPa,黏聚力为12 kPa,内摩擦角为20°,模型计算参数参照文献[1]确定。
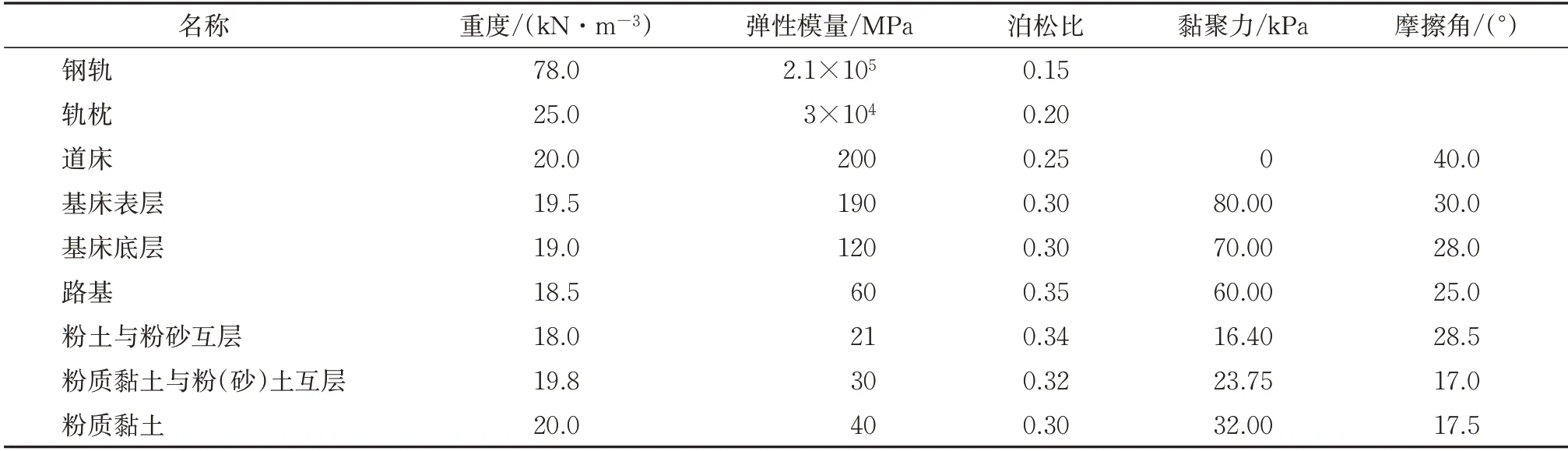
表2 各结构及地层材料计算参数
材料阻尼采用瑞利阻尼,即

式中:C,M和K分别为阻尼矩阵、质量矩阵和刚度矩阵;a0为质量比例阻尼;a1为刚度比例阻尼。
为确定阻尼常数a0和a1的值,需要先确定阻尼比ξ和结构固有频率,得到结构的2 个固有频率ωm和ωn以及阻尼比ξ,代入式(2)即可求得。
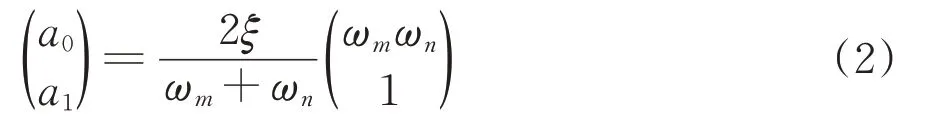
四周采用黏弹性人工边界条件,使得波动能量能够在边界处被逐渐吸收而不会产生反射。
3 荷载模拟
本文的主要研究对象是路基结构,因此列车振动荷载在模拟时不考虑轨道不平顺,车轮偏心,扁疤等各种复杂因素引起的列车荷载的变化,将列车荷载等效为按CRH380A 系列高铁列车车轮位置排列,以时速v移动的周期性轮轴荷载,激振力荷载Pd按下式计算。

式中:Ps为车轮静载,kN;α为速度放大系数,一般取0.004;v为列车时速,km·h-1。
计算中,单边车轮静荷载Ps取75 kN,行车速度为250 km·h-1时,采用上述列车荷载模拟方法绘制出的激振力荷载时程曲线如图4所示。
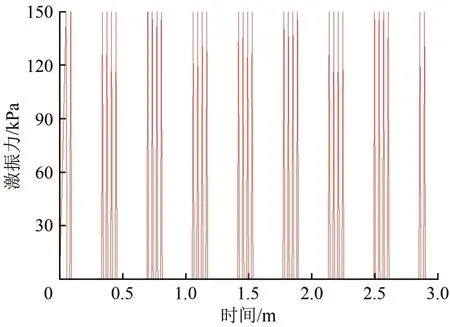
图4 激振力荷载时程曲线(v=250 km·h-1)
4 路基动力响应
本文主要研究列车以速度为250 km·h-1的单线行车(下行)、双线对向行车2 种条件下跨地裂缝带高铁路基及地层垂向动力响应,以及列车以不同车速(60,120,180,250 和300 km·h-1)双线对向行车时对地裂缝带上、下盘路基垂向动力响应的影响。
4.1 动位移
4.1.1 动位移纵向分布
图5给出了基床表层、基床底层、路基本体在单线行车和双线对向行车2 种条件下最大动位移沿路基纵向的变化曲线。由图5可知:单线行车条件下路基最大动位移在地裂缝带附近出现台阶或错台突变现象,呈现出上盘增大、下盘减小的趋势;对向行车条件下路基的动位移明显大于单线行车,且沿纵向呈波形变化,地裂缝带对路基动位移影响相对较小,可能是双线对向行车时列车振动荷载导致的地裂缝带上、下盘土体相互挤压效应减弱所致。
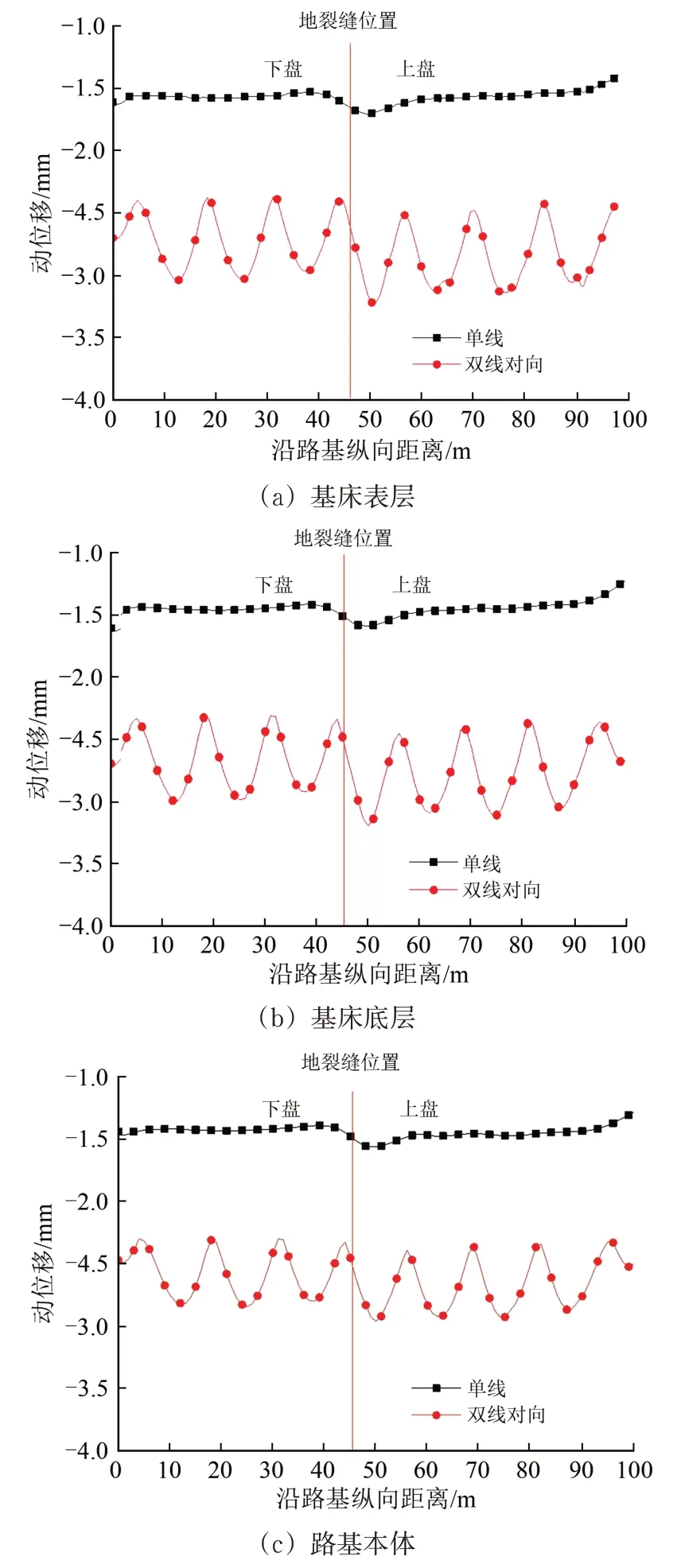
图5 2种行车条件下路基各结构层最大动位移纵向变化曲线
图6给出了路基以下20 m 处最大动位移纵向变化曲线。由图6可知:单线行车和双线对向行车时路基以下20 m 处最大动位移变化规律基本一致,未出现显著波动变化特征,说明列车荷载对路基内动位移影响较大,而对地基内动位移影响较小,但在地裂缝带附近突变现象仍然存在。
4.1.2 地裂缝带上、下盘地表动位移横向分布
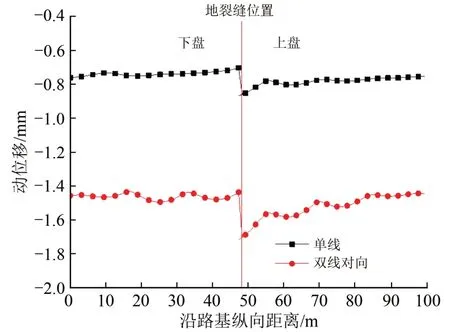
图6 2种行车条件下路基下20 m处最大动位移纵向变化曲线
图7给出了地裂缝带两侧各1 m 处上、下盘地表动位移沿横向的变化曲线。由图7可知:从整体上看,地表动位移及其衰减速度在地裂缝带上盘均稍大于下盘。单线行车时动位移横向呈对称分布,且出现2 个峰值点,位于2 条钢轨正下方;对向行车时动位移横向也呈对称分布,但出现4个位于钢轨正下方的峰值点。
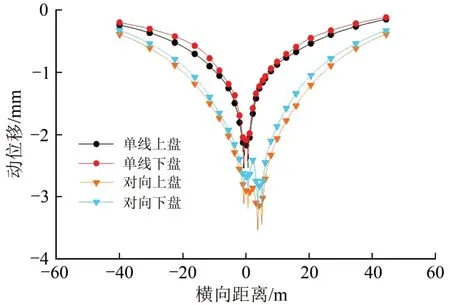
图7 地裂缝带上、下盘地表动位移横向变化曲线
4.1.3 地裂缝带上、下盘动位移垂向分布
图8给出了地裂缝带两侧各1 m 处上、下盘路基动位移垂向(以轨面为0 点,下文同)变化曲线。由图8可知:2 种行车条件下竖向动位移垂向衰减规律大致相同,上盘动位移稍大于下盘,衰减速度在路基范围内变化不大,进入地基以后,衰减速度趋缓,且上、下盘的差减小。
图9给出了路基动位移的垂向衰减拟合曲线。
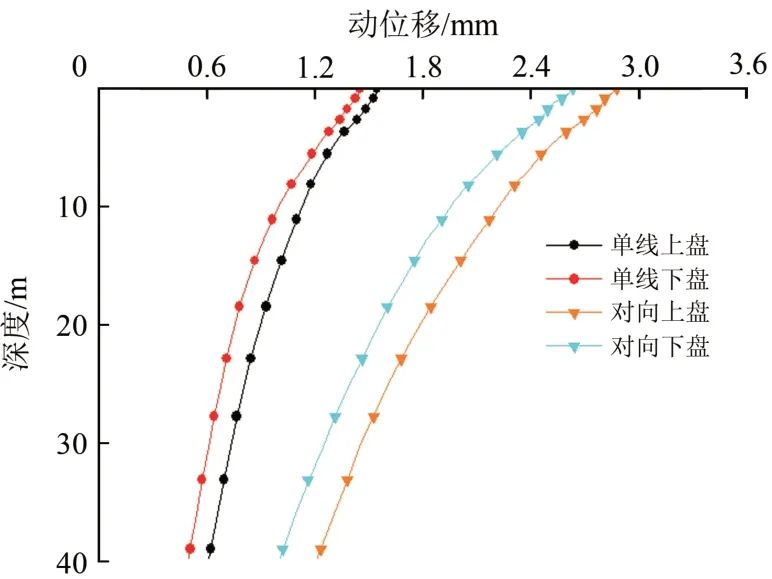
图8 地裂缝带上、下盘动位移垂向衰减曲线
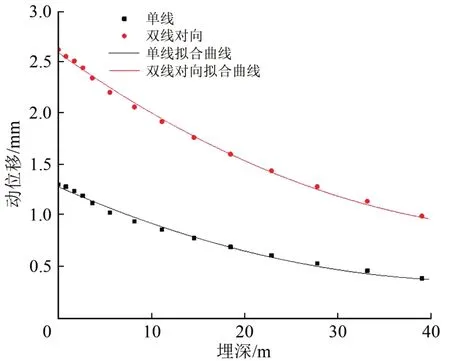
图9 动位移沿深度衰减拟合曲线
由图9可知:动位移s与深度h之间满足2次函数关系。拟合得到的单线行车动位移s单和双线对向行车动位移s双分别为
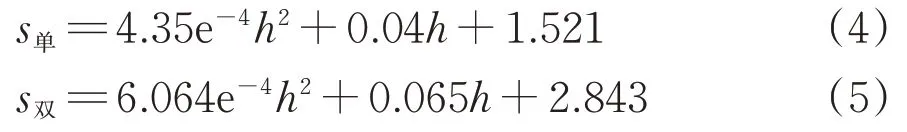
拟合曲线相关系数分别为0.993 和0.997,拟合精度较好。
4.2 动加速度
4.2.1 动加速度纵向分布
图10给出了基床表层、基床底层、路基本体在单线行车和双线对向行车2 种条件下最大动加速度沿路基纵向的变化曲线。
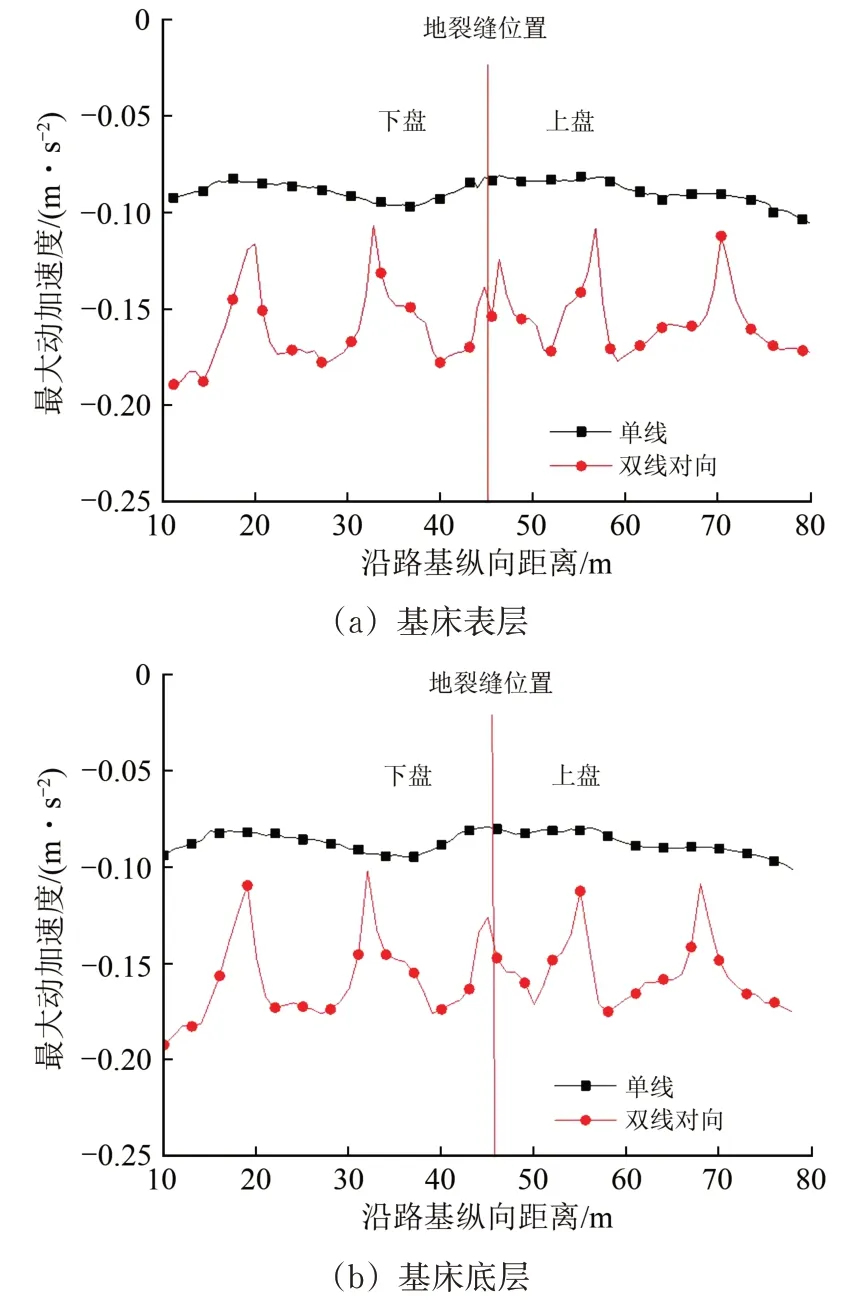
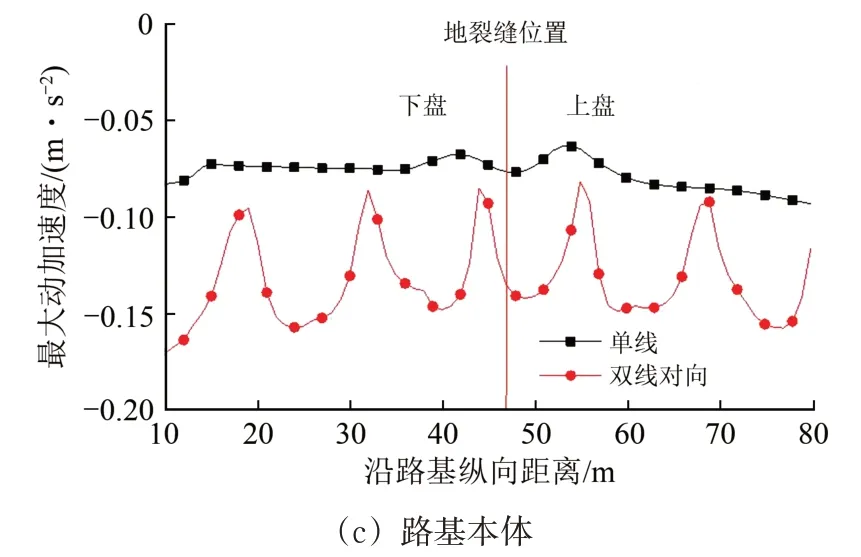
图10 2 种行车条件下路基各结构层最大动加速度纵向变化曲线
由图10可知:与动位移的变化规律类似,单线行车时动加速度响应沿纵向变化平缓,受地裂缝带场地影响小;而双线对向行车时路基各结构层动加速度纵向变化曲线呈波动状。
图11给出了路基下20 m 处最大动加速度沿路基纵向的变化曲线。由图11可知:单线行车时地基动加速度在地裂缝带位置形成错台,出现突变现象,且上盘明显大于下盘;而双线对向行车时地基加速度呈波动变化,在地裂缝带出现显著增大现象,但地基内的动加速度幅值明显小于路基各结构层,说明列车振动荷载作用对路基内动加速度影响显著,而对地基内动加速度影响较小,但在地裂缝带位置附近突变现象仍然存在。
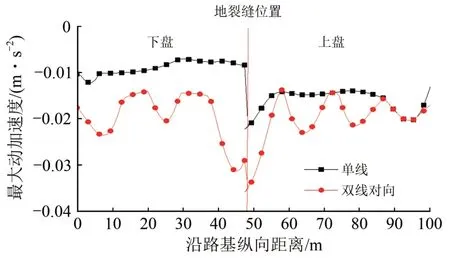
图11 2 种行车条件下路基下20 m 处最大动加速度纵向变化曲线
4.2.2 地裂缝带上、下盘地表动加速度横向分布
图12给出了地裂缝带两侧各1 m 处的上、下盘地表动加速度沿横向的变化曲线。由图12可知:基本与动位移变化规律一致,且上盘动加速度幅值及衰减速度均稍大于下盘。
4.2.3 地裂缝带上、下盘动加速度垂向分布
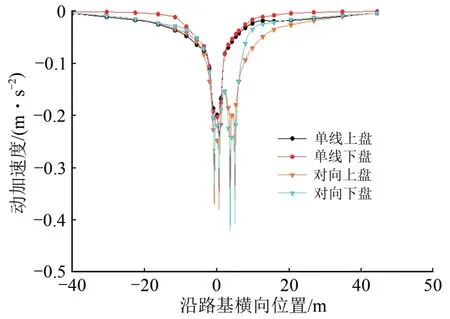
图12 地裂缝带上、下盘动加速度横向变化曲线
图13给出了地裂缝带两侧各1 m 处的上、下盘路基竖向动加速度的变化曲线。由图13可知:竖向动加速度在基床表层衰减速度较平缓,进入基床底层后衰减较快,且上盘动加速度略大于下盘。在基床表层以下的深度范围,对向行车时的动加速度衰减速度要比单线行车时的小,而进入地基以后,二者的衰减速度趋于一致;对向行车条件下,上、下盘动加速度响应差在深度约10 m 时达到最大,随着振动的向下传递越来越小,逐渐趋于一致,在埋深20 m 位置处,地裂缝带上、下盘动加速度曲线趋于重合,此处上盘动加速度衰减了82.34%,下盘动加速度衰减了79.14%,动加速度响应几乎可以忽略,由此可见双线对向行车条件下,地裂缝带地段列车振动荷载作用下动加速度临界影响深度为20 m;单线行车条件下,在深度20 m 位置处,上盘动加速度衰减了79.43%,下盘动加速度衰减93.54%,其临界影响深度为20 m,且上、下盘的差要比双线对向行车条件下大,说明在对向行车条件下,进入地基后振动荷载发生了叠加效应,导致上、下盘的差变小。
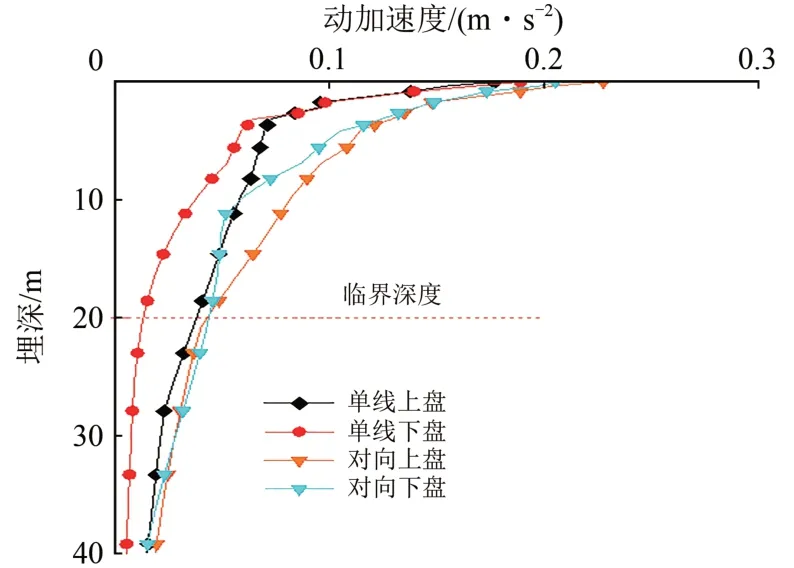
图13 地裂缝带上、下盘竖向动加速度变化曲线
4.3 动应力
4.3.1 动应力纵向分布
图14给出了基床表层、基床底层、路基本体在单线行车和双线对向行车2 种条件下最大动应力沿路基纵向的变化曲线。由图14可知:单线行车时地裂缝带两侧路基动应力幅值跳跃明显,呈现上盘减小、下盘增大的趋势,这与地裂缝带附近上盘地层相对下盘较破碎有关;对向行车时路基动应力沿纵向呈波动变化,地裂缝带附近也即2 车交汇处,出现动应力骤增的现象,应力幅值显著增大,基床表层为15.83 kPa,相较于单线行车时的10.79 kPa 增长了46.7%,而基床底层地裂缝带位置为14.41 kPa,相较于单线行车时的8.86 kPa 增长了62.5%,因此考虑对向行车时列车荷载作用,地裂缝带位置应加强路基结构设计。
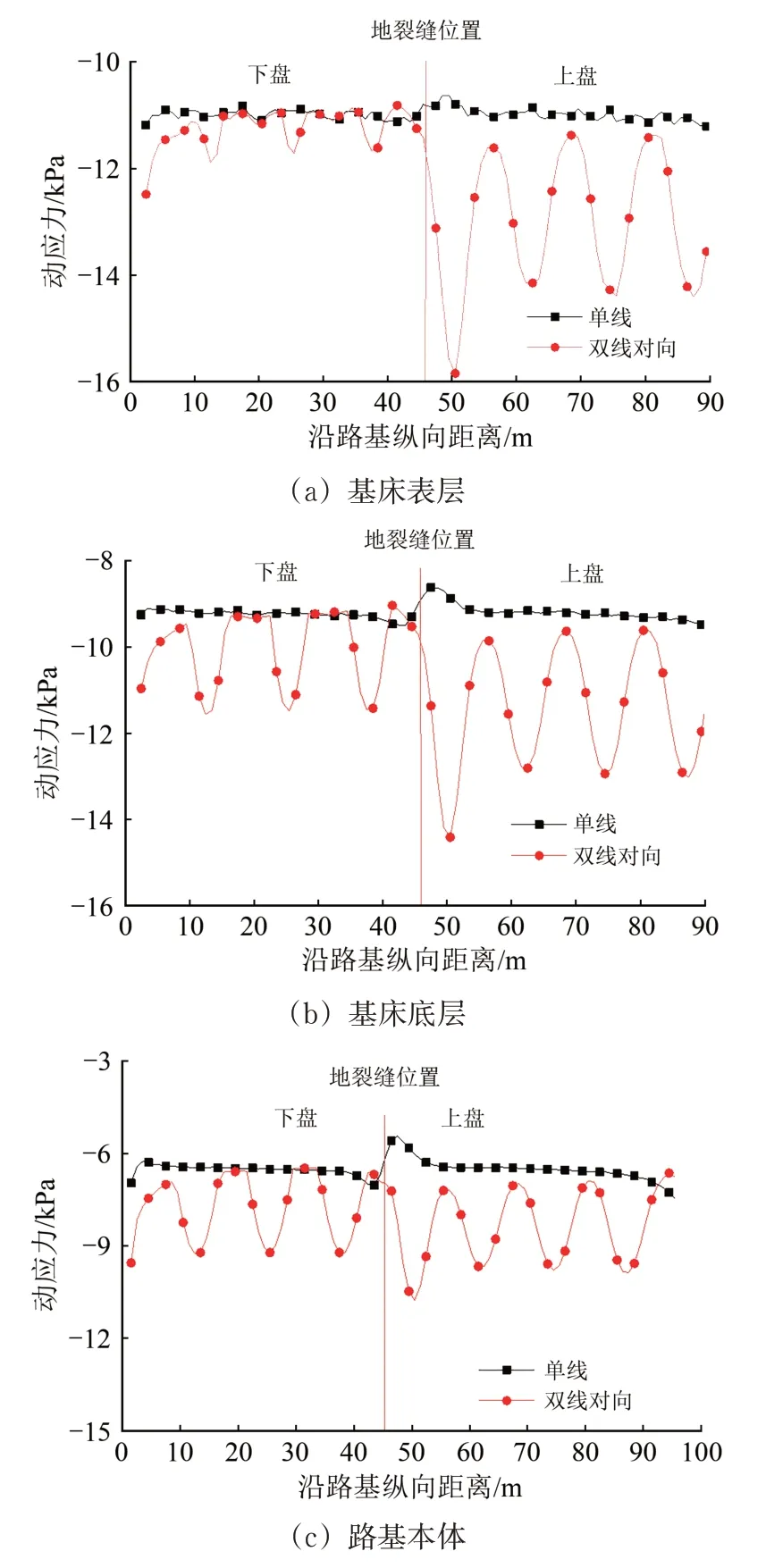
图14 2种行车条件下路基各结构层最大动应力纵向变化曲线
图15给出路基下20 m 处最大动应力沿路基纵向的变化曲线。由图15可知:在路基下20 m 处动应力也出现了与路基各结构层相同的变化规律,但动应力幅值显著减小。
4.3.2 地裂缝带上、下盘动应力垂向分布
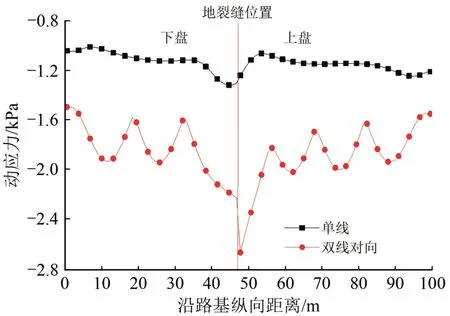
图15 2种行车条件下路基下20 m最大动应力纵向变化曲线
图16给出了地裂缝带两侧各1 m 处上、下盘动应力垂向变化曲线。由图16可知:2种运行方式下动应力垂向变化规律基本一致,在路基结构层内衰减速率较快,进入地基后衰减速度放缓,上盘动应力衰减幅度大于下盘,且在深度为5~15 m 范围内地裂缝带上、下盘动应力幅值相差较大;当深度超过15 m时,2种行车条件下上、下盘动应力幅值差减小。单线行车条件下,在深度25 m 位置处,上盘动应力衰减了81.03%,下盘动应力衰减了86.19%;双线对向行车条件下,在深度35 m 位置处,上盘动应力衰减了86.28%,下盘动应力衰减了82.30%。由此可见,地裂缝带地段列车振动荷载作用下单线行车路基动应力临界影响深度为25 m,双线对向行车条件下为35 m。
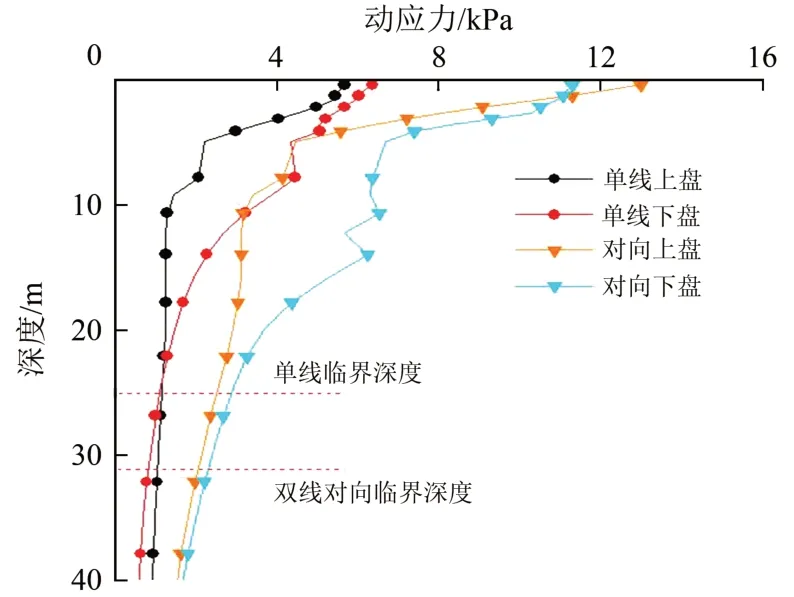
图16 地裂缝带上、下盘竖向动应力幅值变化曲线
4.4 不同车速时路基动力响应
图17给出了基床底层在不同车速下距地裂缝带两侧各1 m 处的上、下盘动位移、动加速度和动应力的变化曲线。
由图17(a)可知:随着车速提高,动位移均呈线性增加,上盘动位移的增速稍大于下盘,上、下盘动位移与行车速度的关系满足1 次函数关系。拟合得到的上盘动位移s上和下盘动位移s下分别为
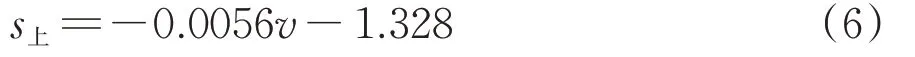
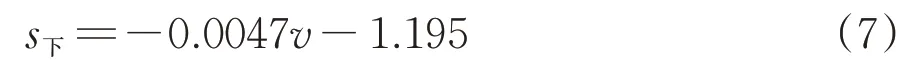
拟合曲线相关系数均大于0.9,拟合精度较好。
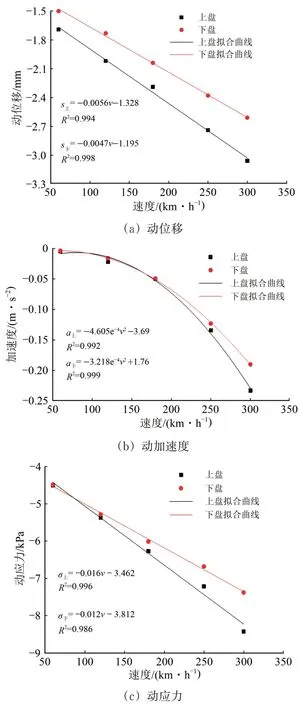
图17 不同速度下地裂缝上、下盘路基动力响应曲线
由图17(b)可知:路基动加速度随着车速呈非线性增加,上盘动加速度的增速稍大于下盘,上、下盘加速度与行车速度的关系满足2 次函数关系。拟合得到的上盘动加速度a上和下盘动加速度a下分别为

拟合曲线相关系数均大于0.9,拟合精度较好。
由图17(c)可知:路基动应力随着车速呈线性增加,上盘动应力的增速稍大于下盘,上、下盘动应力与行车速度的关系满足1次函数关系。拟合得到的上盘动应力σ上和下盘动应力σ下分别为

拟合曲线相关系数均大于0.9,拟合精度较好。
综上可知:动位移和动应力与行车速度满足1次函数关系,动加速度与行车速度满足2 次函数关系;行车速度的增加对列车荷载作用下地裂缝带上、下盘路基动力响应影响显著,因此,建议列车通过地裂缝带路基时应采取减速措施来降低地裂缝带对路基长期稳定性和平顺性的影响。
5 结 论
(1)双线对向行车时路基动位移沿纵向分布呈波形,且上盘略大于下盘,而单线行车时路基动位移变化平稳,仅在地裂缝带位置处出现轻微错台现象,2 种行车条件下路基动位移沿垂向衰减均满足2次函数关系。
(2)双线对向行车时路基动加速度沿纵向分布呈波形,横向分布上盘略大于下盘,且上盘衰减速度大于下盘,而单线行车时沿纵向路基各结构层加速度较平稳,地基内地裂缝带位置出现明显错台现象;单线行车和双线对向行车条件下上、下盘动加速度影响临界深度为20 m。
(3)双线对向行车时路基动应力沿纵向分布呈波形,在地裂缝带附近出现动应力骤增的现象,单线行车和双线对向行车条件下天然地基地裂缝带场地路基动应力影响临界深度分别为25和35 m。
(4)地裂缝带上、下盘路基动位移和动应力与行车速度满足1次函数关系,而动加速度与行车速度满足2次函数关系。
