高速磁浮轨道不平顺检测系统去噪算法
2020-10-17
(国防科技大学 智能科学学院,湖南 长沙 410073)
高速磁浮列车是一种与轨道无接触运行的地面飞行器,列车的运行安全性、稳定性和舒适性均高度依赖轨道的平顺状态。为保持轨道良好,需定期进行轨道不平顺检测并施加维护。目前,上海高速磁浮运营线使用的轨道检测系统是德国GMS 系统(Guideway Monitor System),国内引进消化后研制了TIS 系统[1],2 种系统均利用车载间隙传感器和加速度传感器、使用惯性基准法实现对轨道的短波、长波不平顺进行测量。
高速磁浮轨道检测系统的轨道不平顺信号处理方法主要包括线性相位IIR 移变滤波器[2],异常点剔除、平滑、拟合及趋势项消除预处理[3],利用经验模态分解对特定频率分量进行提取[4],小波变换阈值处理[5]等。以上研究方法并没有考虑由于轨道结构和车辆运行姿态等因素引入的测量噪声,而是对所有噪声进行了统一处理,缺少针对噪声的分类和针对性处理。系统测量信号的信噪比很大程度上决定了检测系统整体的测量精度。
国防科大研制的搭载式高速磁浮轨道不平顺检测系统如图1所示,系统中2 个测量模块分别安装在列车头车的左、右侧电磁铁前端盖处,与电磁铁固连可视为整体。该系统基于惯性基准法原理,利用激光位移传感器测量轨道定子面与系统距离,并依靠加速度计和陀螺仪补偿由于系统姿态变化引入的测量偏差。由于搭载式高速磁浮轨检系统采用了不同的传感器类型、测量方式和安装环境,导致系统在信号处理上与GMS 系统存在差异,主要体现在对测量信号的去噪处理层面。

图1 搭载式高速磁浮轨道不平顺检测系统(模块)
本文结合高速磁浮轨道的结构特点和高速磁浮轨道不平顺检测系统搭载式的安装特点,分析系统传感器输出测量信号包含的噪声的来源及特点,分别去除齿槽纹波噪声、轨缝脉冲噪声和悬浮振动噪声,同时提出基于改进经验模态分解的自适应阈值去噪算法[6],可在去噪的同时较好地保留轨道梁接缝信息,以便于轨检系统进行里程修正。此外,借助协方差、信噪比、信噪比增益及平滑度4项指标评价去噪效果。
1 噪声来源及特点
除检测过程中广泛存在的高频噪声外,因高速磁浮轨道结构特点以及列车的运行特点,还存在以下2种噪声。
1.1 结构噪声
高速磁浮轨道多采用长定子结构,如图2所示,单个跨粱长24.768 m,相邻跨粱间有90~100 mm 的轨道梁接缝[6];轨道悬浮面由连续拼接的定子组成,相邻2 个定子间也存在接缝,定子接缝宽约2.5~5.0 mm;定子具有特殊的齿槽结构,槽用于镶装电缆,而齿则用于导通电磁力。
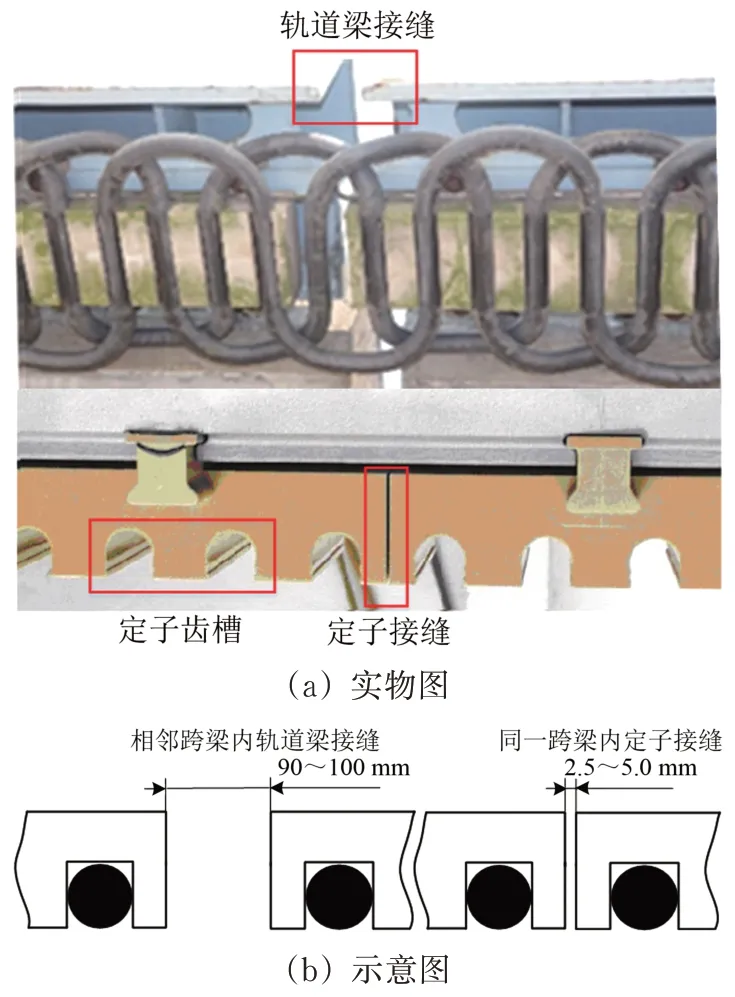
图2 磁浮轨道长定子结构
当激光位移计处于轨道接缝(轨道梁接缝和定子接缝)位置时,由于激光空射的原因,传感器的输出将达到饱和,导致测量结果出现脉冲,且接缝宽度越大,脉冲宽度也越大。使用激光位移计测量定子面的高度时,理论上测量的轨道定子面高度应为齿面高度,但由于齿槽结构的影响,使测量点不可避免落在槽内线缆上,测量结果存在齿槽纹波,将导致轨道不平顺计算失真。
将轨道梁接缝和定子接缝及定子面齿槽结构引入的噪声均定义为结构噪声。
1.2 低频悬浮振动噪声
轨道不平顺检测装置搭载在列车电磁铁上,在检测运行过程中由于车辆存在悬浮振动,使得测量结果包含不同波长的低频振动。车辆敏感自振频率与轨道不平顺波长的关系见表1。由表1可以看出,车辆的自振频率范围为0.8~2 Hz 时,在测量结果中随车速的不同引入不同波长的轨道不平顺信息,干扰轨道不平顺的正常测量。车辆悬浮振动引入噪声定义为低频悬浮振动噪声。

表1 车辆敏感自振频率与轨道不平顺波长的关系
2 去噪算法设计
结构噪声和低频悬浮振动噪声导致系统测量结果失真,需对测量信号进行去噪处理。结构噪声中,轨道梁接缝引入的脉冲噪声按固定粱跨间隔周期分布,因其里程位置固定,可用于里程定位校准,予以保留[7]。
对于激光位移传感器采集的原始信号,按照原始信号→去除齿槽纹波和定子接缝引入的结构噪声→平滑处理→去除低频悬浮振动噪声的流程进行噪声去除。
2.1 结构噪声去除算法
采取对测量值进行阈值判断的方法去除结构噪声,即将进入槽面和定子接缝内的信息用上一个定子面均值代替,以消除齿槽纹波及定子接缝的噪声,对进入轨道梁接缝的信息予以保留,具体算法流程如图3所示。
激光位移传感器的采样间隔为2 mm 时,可以得到较好的槽面和定子接缝信息。以2 mm 采样间隔生成包含齿槽面、定子接缝及轨道梁接缝的理想数据,其中齿槽面数据以半径为20 mm 的半圆代替。理想状态下的齿槽及接缝数据使用结构噪声去除算法处理,数据处理前后对比如图4(a)所示。结果表明,处理后的齿槽纹波干扰和定子接缝干扰已完全去除,同时保留轨道梁接缝信息,表明了结构噪声去除算法的有效性,可为辅助定位和轨道梁接缝宽度测量提供依据。
考虑惯性基准法的检测精度和车辆摇头、点头、侧滚等运动对激光位移传感器的影响[8],在理想的齿槽及接缝数据中叠加整个频带范围内的高斯白噪声,功率为-3 dB,模拟激光位移传感器的实际输出;再使用结构噪声去除算法处理数据,数据处理前后对比如图4(b)所示。结果表明,处理后的数据基本消除了齿槽波纹和定子接缝引入的结构噪声,仅有少量齿槽结构噪声未完全去除,残余结构噪声和高频噪声可采用改进经验模态分解(Improve Empirical Mode Decomposition,EEMD)方法去除。
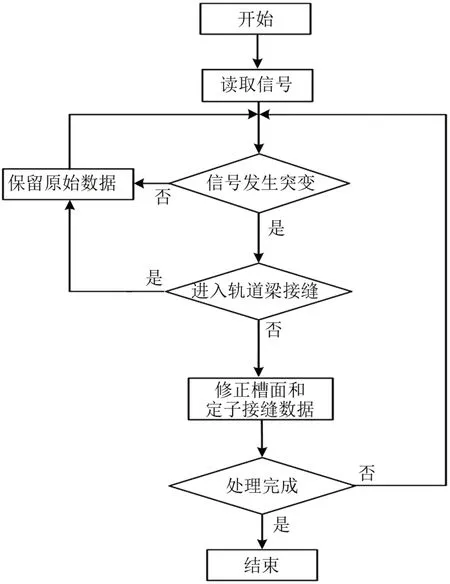
图3 结构噪声去除算法流程图
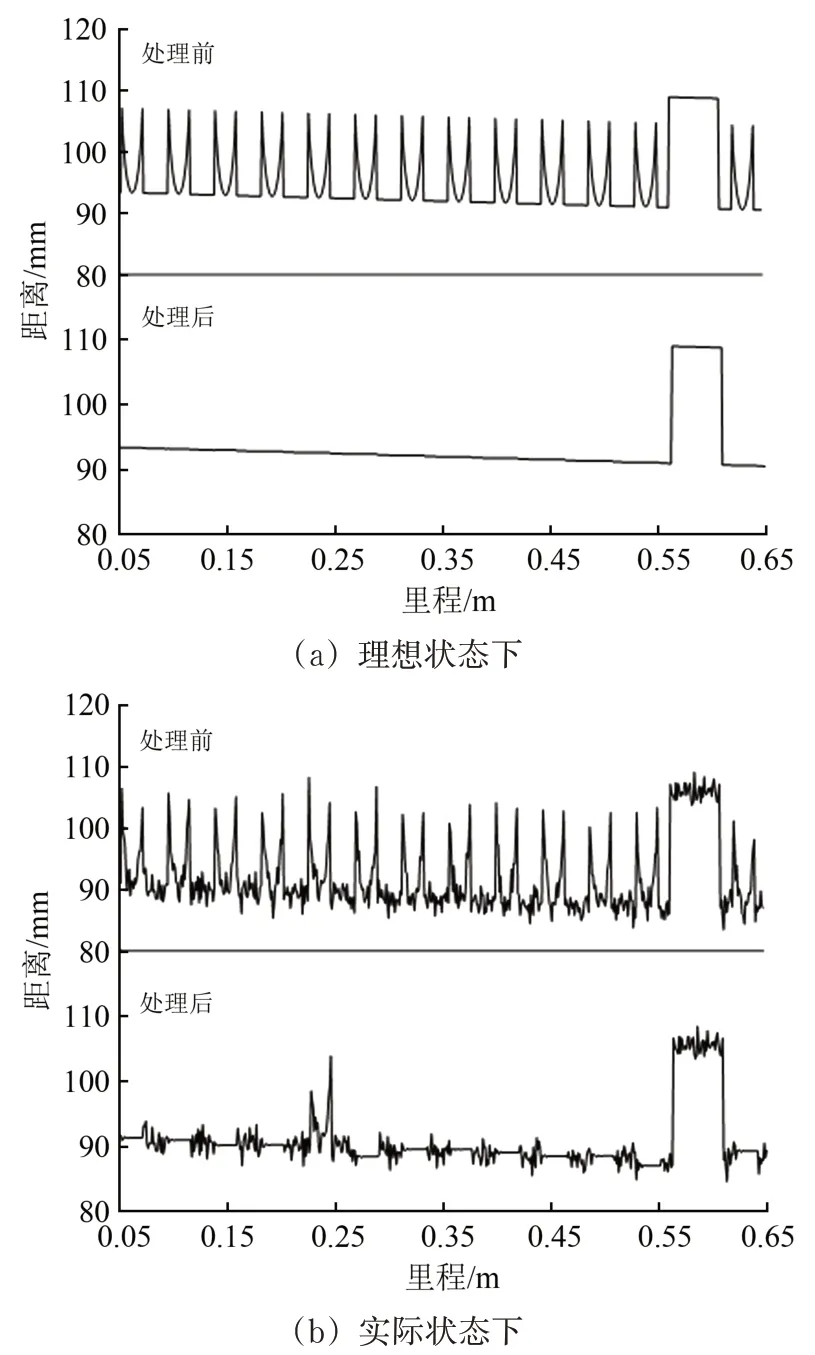
图4 结构噪声处理结果
2.2 高频噪声和残余结构噪声去除算法
EEMD 可将原始信号分解成若干个本征模函数IMFs,每个分量包含原始信号中不同的频率和幅值信息[9],由此可将有用信号和噪声信号分解。EEMD 分解后的分量个数由原始信号的客观复杂程度决定,避免了小波基和分解层数需要人为选择而引入主观误差。
利用EEMD 对去除结构噪声后的信号进行分解,通过计算高低频分量的分界点,同时借鉴小波去噪中的软阈值方法,实现只对高频分量添加不同的阈值,再进行信号重构和端部处理,完成高速磁浮轨道不平顺信号高频噪声和残余结构噪声的去噪处理。
2.2.1 高低频分界点确定方法
经验模态分解后的IMFs,其高频分量代表噪声信号,具有幅值和离散程度小、平均周期短、与原信号相关性差的特点;低频分量则代表有用信号,包含轨道不平顺信息,具有离散程度大、平均周期长、与原信号相关性高的特点。分别计算分解后各IMFs 的方差、能量、相关系数(与原信号的相关性)和平均周期,对结果归一化后找到这些信息发生较大转折的点,将其作为高低频信号的分界点,如图5所示。由图5可以看出:高低频分量之间存在较大的分界点,分别计算各项指标的均值,找到第1个大于均值的分量序列并将其作为高低频信号的分界点,对高频分量添加阈值、低频分量予以保留。
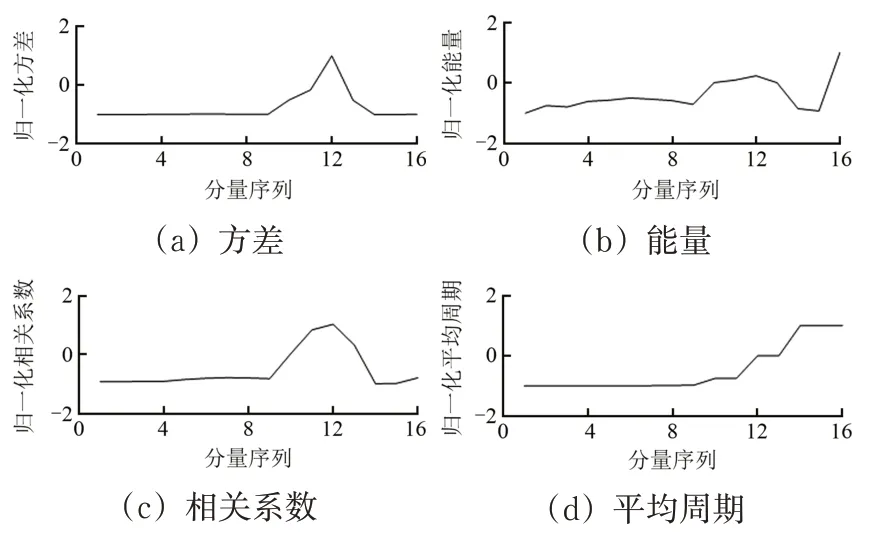
图5 高低频分界点分析
2.2.2 阈值设定
自然噪声可认为服从高斯分布,少量残余的齿槽纹波和定子接缝数据为需要去除的噪声信号,其幅值较小;轨道梁接缝引起的低频脉冲信号为需要保留的有用信号,其幅值相对较大。总体来说,高频分量对应的幅值可认为服从高斯分布。以分解后的分量8 为例,其幅值大小和分布情况如图6所示。由图6可以看出:信号中大部分为噪声信号,轨道梁接缝按25 m 间隔分布;分量8 的幅值呈高斯分布,因此其阈值的选择需满足2 个条件:①去除大部分高频的干扰信息;②较完善地保留轨道梁接缝信息。

图6 分量8幅值大小和分布情况
采用3ơ原则[10]计算阈值大小,即将幅值处于(-3ơ,3ơ)范围内的信号置0,保留约0.3%的轨道梁接缝数据。
选取适当的阈值后,采用软阈值方法作用于信号中。软阈值在硬阈值的基础上,将信号边界出现的不连续点收敛到零,去噪后能产生更光滑的结果[11]。
2.3 低频悬浮振动噪声去除算法
激光位移传感器的输出信号经上述过程处理后,依旧包含影响较大的低频悬浮振动噪声。根据惯性基准法原理,对去除结构噪声和高频噪声后的信号进行积分,得到垂向振动的位移信号,将其从激光位移传感器信号中去除,即可得到实际的定子面不平顺信息。系统采用离线处理的方式,故对数据的实时性不做要求,因此选取频域积分法对加速度数据进行积分。
频域积分将信号做傅里叶变换,然后在频域中对感兴趣的频段对信号进行处理,无须再像积分滤波法一样在积分前对数据进行解偏滤波,或像时域法一样在积分后消除信号的趋势项。
3 仿真结果
按照磁浮轨道的标准尺寸仿真了8 段梁间轨道,总长为199.156 m,其中梁间轨道长24.814 m,梁间轨道接缝为92 mm;同一梁间由24 个定子构成,定子长1.032 m,定子接缝为2 mm;每个定子由12 个齿槽结构构成,每个齿槽结构为86 mm,其中齿面为46 mm,槽面为40 mm。以梁间轨道长度为单位,分别添加25,50 和100 m 的轨道长波不平顺,幅值分别为6,8 和10 mm[12]。在实际检测过程中,搭载设备随同列车一起振动,车速为100 km·h-1,自振频率为2 Hz,添加波长为13.9 m、振幅为5 mm 的车体低频振动,并添加信噪比为-3 dB 的高斯白噪声模拟自然噪声,进行2 mm 采样。仿真得到的轨道不平顺期望信号和模拟激光位移传感器输出的原始信号如图7所示。
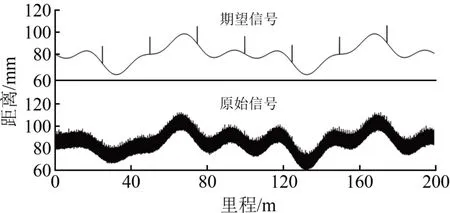
图7 轨道不平顺仿真信号
采用高速磁浮轨道不平顺检测系统去噪算法对轨道不平顺原始信号进行处理,结果如图8所示。由图8可以看出:采用2.1 和2.2 部分算法处理后的信号仅存在少量残余结构噪声和低频悬浮振动噪声;采用2.3 部分算法处理后得到真实的轨道不平顺信息,与期望信号基本重合,只在轨道梁接缝处存在较大波动。
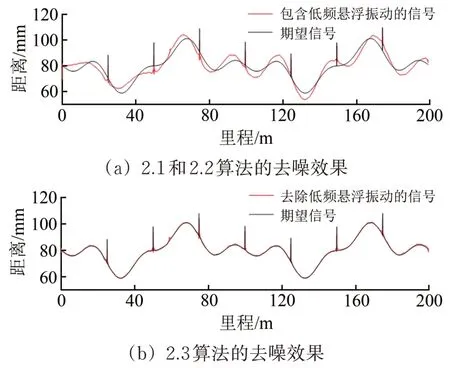
图8 轨道不平顺去噪处理结果
对5 组添加不同噪声的数据进行处理,分别计算各项去噪指标,结果见表2。从表2可以看出,经过该去噪算法处理后信号各方面均达到较高标准,尤其是信噪比增益提高约1倍,表明高速磁浮轨道不平顺检测系统去噪算法的有效性。
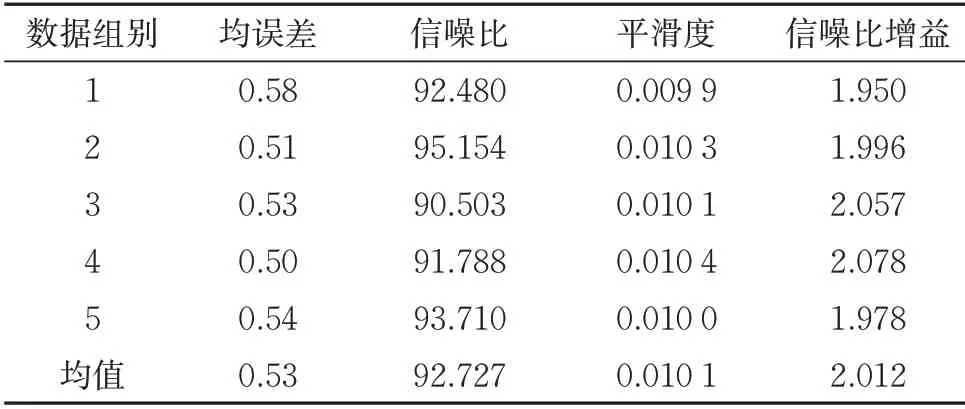
表2 去噪效果评价指标计算结果
4 结 论
(1)分析了高速磁浮轨道检测系统测量信号的噪声来源,并根据结构噪声和低频悬浮振动噪声的特点设计了噪声去除算法。在保留由轨道梁接缝引入噪声的前提下,可有效减小因齿槽结构和定子接缝引起的噪声。
(2)利用仿真验证了经验模态分解算法针对高频噪声的有效性,在此基础上设计了自适应阈值的方法,实现对高低频分量分步处理。
(3)利用EEMD 去除高频噪声、剩余定子接缝脉冲噪声和未去除的齿槽纹波噪声,同时保留轨道梁接缝信号的脉冲尖峰特性。仿真表明EEMD算法可有效去除系统测量过程中由于轨道结构和系统搭载环境引入的噪声,信噪比增益提高约1倍。
