基于周期结构法的弹性短轨枕轨道声振特性分析

2020-10-17徐涆文刘晓龙梁树林陈秉智

中国铁道科学 2020年5期

徐涆文，韩健，刘晓龙，田彩，梁树林，陈秉智

（1.西南交通大学牵引动力国家重点实验室，四川成都 610031；2.大连交通大学机车车辆工程学院，辽宁大连 116028）

随着国内列车运行速度的不断提高，以及城市轨道交通的迅猛发展，人们对于轨道的减振降噪性能要求也越来越高。轨道作为主要的噪声和振动源之一，国内外研究人员对其振动和声辐射特性也进行了大量研究［1-2］。大量的减振型轨道也随之产生，并被铺设于振动噪声要求较高的路段，减振型无砟轨道由于其良好的减振降噪性能，运用在我国的地铁、轻轨以及城际铁路上。弹性短轨枕轨道即为减振型轨道的1 种。在轨枕下加入轨下弹性垫层，提高了弹性短轨枕轨道结构的减振和降噪性能，同时其具有结构简单，施工方便，轨枕下支承刚度易于调整的优点。但是目前对于弹性短轨枕振动和声辐射特性的了解较少，对相关参数选取认知还不够深入。若参数选取不合理则可能无法发挥出其减振作用，甚至会增加轨道振动和声辐射响应，导致车内噪声增大。因此，分析弹性短轨枕轨道不同结构参数对轨道的振动声辐射影响就显得尤为重要。

杨俊斌［3］对2 种弹性支撑轨道进行了各个结构参数对结构稳定性以及高速铁路上的适应性影响分析，确定了高速列车荷载作用下弹性支承轨道各结构参数的合理取值。方锐等［4-5］基于有限元—边界元法建立了有砟轨道垂向振动和声辐射有限元模型，分析了钢轨、轨枕和道床等相关结构参数对轨道振动及其声辐射的影响。王根平［6］基于FEM和BEM 方法对减振型双块式无砟轨道进行了垂向振动特性以及轨道各结构层声辐射效率的分析。

受计算能力限制，在对周期结构进行动态特性分析时，往往需要对周期结构进行有限长度截取，为了消除截取的周期结构边界波动反射对于仿真结果的影响，需要对截取界面选择合理的边界条件。刘晶波，谷音［7-8］基于矩阵等效原理采用有限单元来模拟二维以及三维黏弹性边界单元，以消除边界反射波干扰。而这种边界结构仅适用于材料均匀连续的结构，并不适用于离散支撑的轨道结构。金浩［9］基于谱单元法建立了轨道的元胞模型从而能够较好地表征轨道的“无限长”结构特性，利用模型分析了钢轨动力吸振器对于轨道振动特性的影响。马龙祥［10］利用轨道结构的周期结构特性建立了轨道周期结构模型，分析了轨道结构在移动载荷激励下的振动特性。但是上述2 种轨道结构的钢轨均采用的是经典欧拉梁模型，其不能较好地模拟出实际的钢轨截面形状。同样各种商用有限元软件中也提出了相应的无反射边界单元，但是对于离散支撑的有限元轨道结构其并不能有效地衰减有限截取长度轨道边界的反射波干扰。目前国内消除实体有限元轨道边界反射波的方法多为加长结构计算模型。这达不到降低计算效率的建模初衷。

为了消除有限截取模型的边界弹性波反射的影响，本文基于周期结构原理建立了无反射边界的有限元轨道模型，分析弹性短轨枕轨道的隔振性能、轨道各结构的声辐射特性，并研究不同轨枕下支承刚度对其振动和声辐射特性的影响。

1 轨道周期结构模型

1.1 模型建立

周期结构是由元胞按一定的规律重复排列而形成的结构形式。当组成周期结构的元胞按规律在空间中是无限重复时即形成理想的周期结构［10］。轨道可看作为1种纵向方向的理想周期结构，其中每1 块道床板长度的轨道结构即可看作周期结构中的元胞。图1为运用有限元软件ANSYS 建立的轨道结构元胞有限元模型。

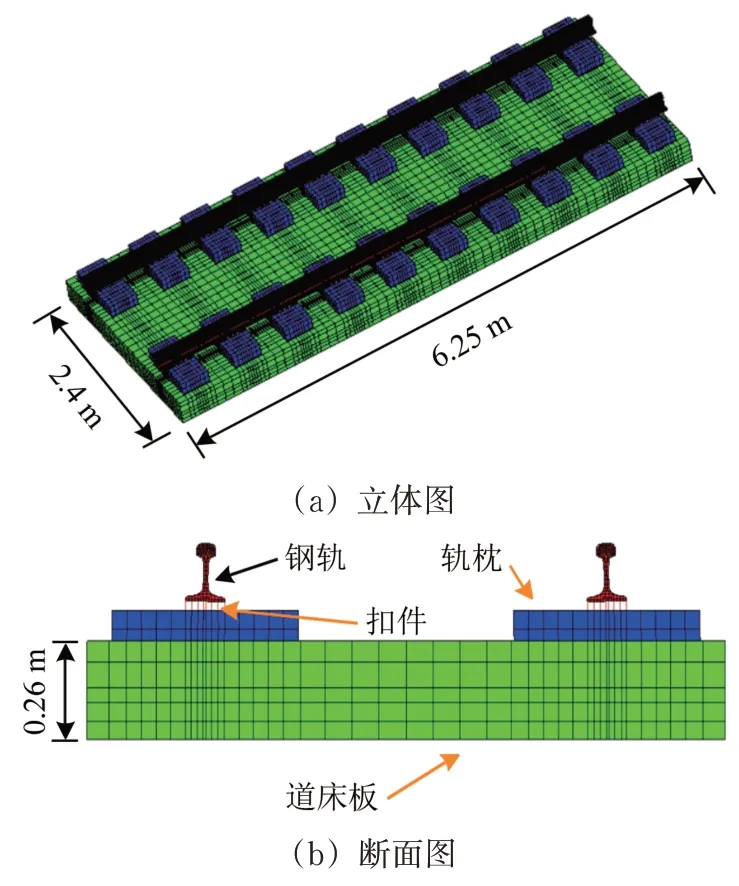
图1 轨道结构元胞有限元模型

在轨道结构元胞有限元模型中，钢轨、轨枕和道床采用实体单元（solid185）进行离散，扣件系统采用线性的弹簧阻尼单元（combine14）进行模拟，其垂向刚度为80 MN·m-1，横向刚度为50 MN·m-1，纵向刚度为40 MN·m-1。模型中，钢轨为UIC60 轨，其弹性模量为210 GPa，泊松比为0.3，质量为60 kg·m-1；轨枕选用SK-1 型轨枕，其弹性模量为35 GPa，泊松比为0.2，质量为90 kg；道床板混凝土设计标号为C55，其弹性模量为36 GPa，泊松比0.2，密度为2 500 kg·m-3。

轨道结构元胞强迫振动动力学方程为［11］

其中，

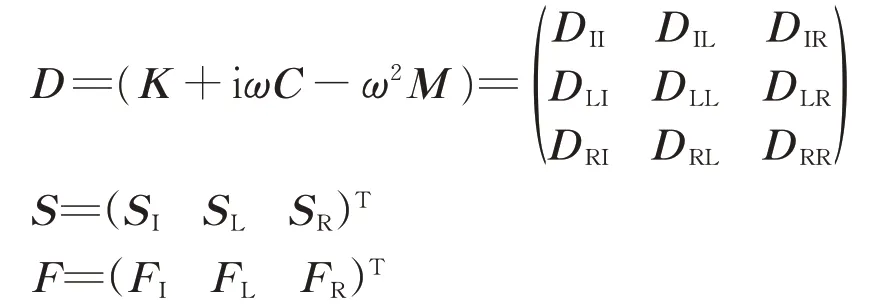
式中：D为轨道结构元胞总动刚度矩阵；S为轨道结构元胞位移矩阵；F为轨道结构元胞受到的作用力向量；C，K和M分别为轨道结构元胞的阻尼矩阵、刚度矩阵和质量矩阵；ω为角频率；SI，SL和SR分别为轨道结构元胞中钢轨中部，左边界，右边界的节点位移；FI，FL和FR分别为轨道结构元胞中钢轨中部，左边界和右边界节点受到的作用力；Dij为对应于元胞结构中部、左边界和右边界节点位移下的局部刚度矩阵，下标i，j=I，L，R。

由于轨道结构元胞的中部不受外激励力的作用，即FI=0。因此可以通过等式SI=-(DILSL+DIRSR)对上述的动刚度矩阵D进行缩聚处理［11］

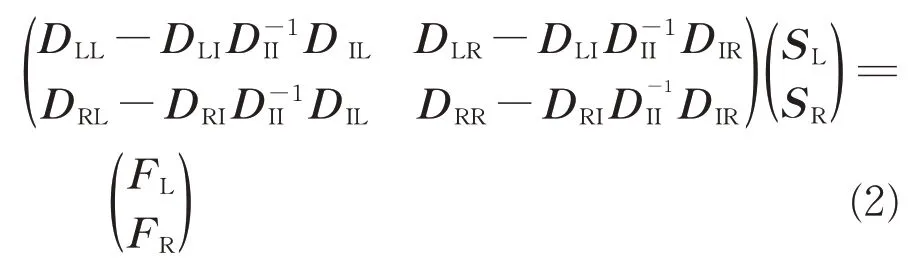
其中，

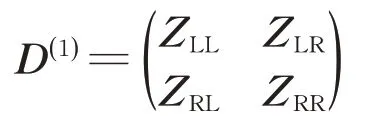
式中：D（1）为经过缩聚后的单个元胞动刚度矩阵。

下面将2 个轨道结构元胞进行组合，有限元模型如图2所示。

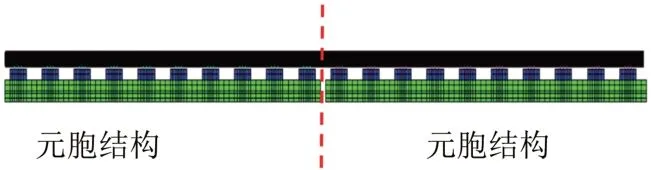
图2 元胞组合结构图

其强迫振动方程为

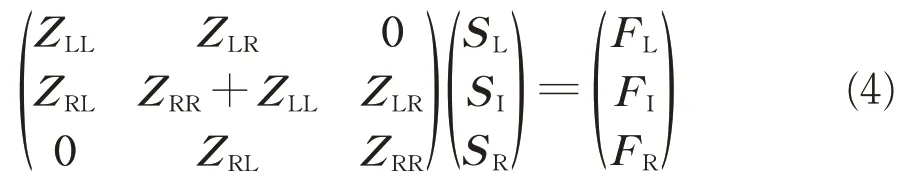
此时2 个轨道结构元胞集合成1 个整体，对新生成的结构刚度矩阵进行缩聚得

其中，

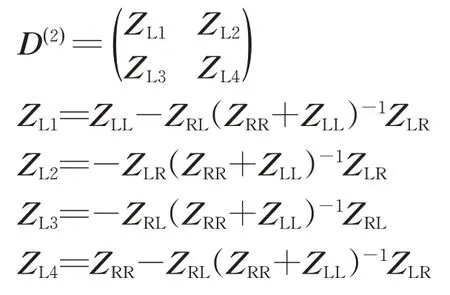
因此对于具有周期性轨道结构，可以通过上述方法进行多个相同元胞叠加，得到理想长度的轨道周期结构总动刚度矩阵与初始激励输入和最终响应输出的关系。最终叠加后的理想周期结构总动刚度矩阵D（n）维度大小同单块道床板长度的轨道结构总动刚度矩阵相同，其中n=1，2，…，N，N为迭代的次数。因此将对应项系数进行替换即可通过单块道床板长度的轨道结构模拟无限长轨道结构的振动衰减特性。

1.2 模型验证

本文研究单位垂向简谐力作用F下的钢轨垂向振动固有特性，激励力作用位置为钢轨跨中的钢轨顶面。为提高计算效率，根据轨道结构的横向对称特性，截取轨道结构横向的一半模型作为计算模型。

轨道是1 种沿纵向方向的周期结构，钢轨顶面在单位简谐力的作用下产生的振动波沿着钢轨纵向向两侧传播，实际中的轨道结构可看作理想的周期结构，弹性波沿着钢轨纵向传播不断衰减最终趋于零［12］。通过周期结构原理对单块道床板长度的轨道模型的边界进行处理以模拟左右两侧无限延长的轨道结构，结构如图3所示。

提取单块道床板长度的轨道有限元模型的动刚度矩阵，根据上一节的方法叠加出理想周期结构轨道的总动刚度，由于此总动刚度矩阵缩聚后矩阵维度同单块轨道板的总动刚度矩阵相同，将多次叠加后的总动刚度矩阵内的对应项参数赋值给单块道床板长度的有限元轨道结构，最后将其加到截取后的轨道有限元结构的边界，从而模拟无限长轨道振动的纵向衰减特性，消除结构边界反射波对于原点响应分析的影响。

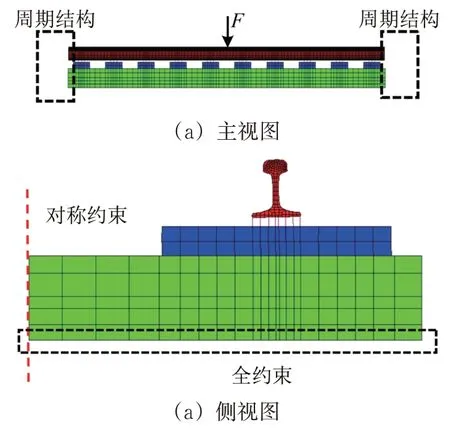
图3 轨道周期结构模型

为了验证计算模型的准确性，对某地铁非弹性轨枕轨道进行力锤敲击试验，获取其频率响应函数，与仿真计算结果进行对比，进而修正有限元模型。试验中，钢轨类型为UIC60，轨枕以及道床板均为混凝土结构，钢轨扣件间距为0.625 m。

轨道结构较复杂，并且轨道频响测试结果会受到较多因素影响，如扣件装配位置精度，钢轨，道床板以及扣件弹性垫等材料的实际属性，测试环境温度等，而仿真模型则是抓住主要的影响因素，采用简化的模型模拟出轨道的实际振动特性。

图4给出了采用3 块和5 块道床板长度有限元轨道模型及周期结构轨道模型计算得到的钢轨垂向加速度导纳。

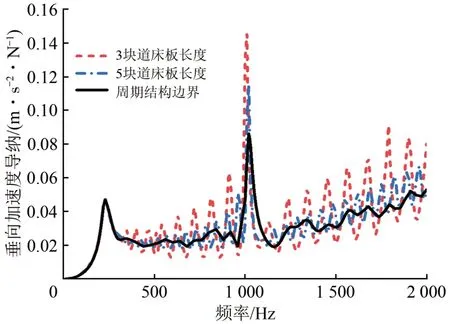
图4 不同轨道模型下的钢轨垂向加速度导纳

由图4可知：加长轨道模型能够较好地缓解边界反射波对钢轨频响函数的干扰，但是过长的轨道模型会给仿真分析带来极大的计算量，而建立的轨道模型周期结构边界能够有效地消除边界反射波的影响，从而大大提升模型的计算效率。

图5给出了钢轨垂向加速度导纳曲线。由图5可知：2 条曲线整体符合程度较高，且曲线随频率变化的趋势也是基本相同；特别是在230和1 020 Hz处仿真和实测结果均出现振动峰，并且振动峰的位置以及大小基本相同。由有限元轨道的模态分析可得这2种峰值对应的模态振型，分别为230 Hz的钢轨垂向1阶振动和1 020 Hz钢轨的Pinned-Pinned振动，与实际的轨道振动模态也是完全符合。因此建立的模型能够较为准确地反映轨道的振动特性，可以利用此模型对轨道的振动以及声辐射特性进行分析。

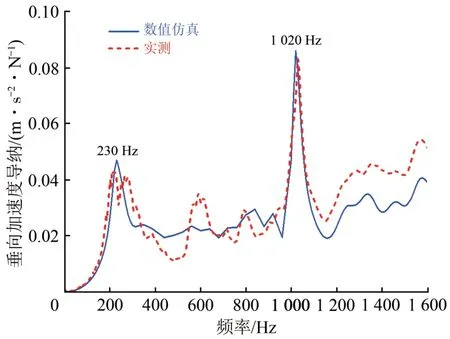
图5 周期结构边界的轨道模型计算和实测的钢轨垂向加速度导纳

2 弹性短轨枕轨道声振特性

弹性短轨枕轨道是1 种减振型轨道结构，同普通的非弹性轨枕轨道相比，弹性短轨枕轨道为了缓解轨道垂向和横向的振动传递，在轨枕下方和轨枕四周加入了轨下弹性垫层和橡胶套结构［3］，如图6所示。

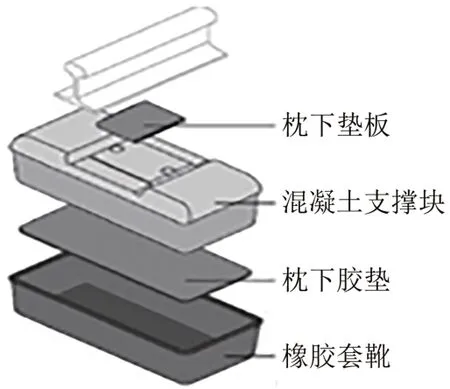
图6 弹性短轨枕结构

为了分析在轨枕下加入轨下弹性垫层后对钢轨振动以及声辐射的影响，在上节验证的刚性道床轨道模型的基础上，在轨枕和道床板之间通过弹簧和阻尼单元进行连接，以模拟实际轨道中的橡胶套和轨下弹性垫层结构，研究轨枕下加入轨下弹性垫层后钢轨的振动特性。根据文献［3］，取轨枕的相关结构参数为：轨枕弹性模量35 GPa，密度2 500 kg·m-3，单块轨枕质量140 kg，泊松比0.2。轨枕的长、宽和高分别为700，320 和250 mm。扣件刚度同上述刚性道床轨道。轨下弹性垫层刚度为120 MN·m-1，轨枕橡胶套刚度为5 000 kN·m-2。弹性短轨枕有限元模型如图7所示。

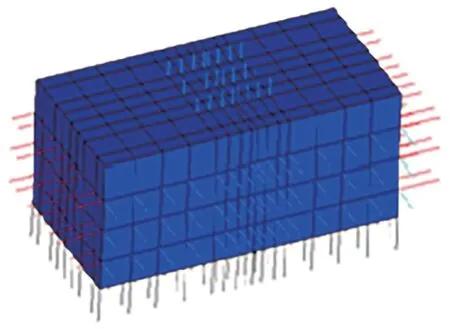
图7 弹性短轨枕有限元模型

2.1 弹性短轨枕轨道振动响应特性

轨道结构的振动特性分析是其声辐射分析的基础，同理基于上述周期结构原理建立具有无反射边界的弹性短轨枕轨道有限元模型，分析其在单位激励力下的振动响应。

图8为弹性短轨枕和刚性道床轨道上激励力作用点处钢轨的加速度导纳。

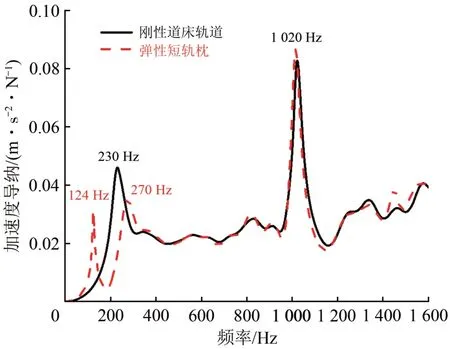
图8 弹性短轨枕轨道激励力作用点处钢轨加速度导纳

由图8可知：2 种轨道上钢轨的加速度导纳曲线除了在0～400 Hz 位置处振动峰有较大差异外，在Pinned-Pinned 振动峰以及其余频率位置钢轨加速度导纳曲线并未受到轨枕下结构改变的影响；在频率为0～400 Hz 的范围内，弹性短轨枕轨道的钢轨激励点垂向加速度导纳曲线出现2 个峰值，峰值频率分别为124和270 Hz。

由轨道结构进行模态分析可知：弹性短轨枕轨道的第1 个峰值为钢轨的1 阶垂向弯曲振动模态，如图9（a）所示，弹性短轨枕轨道中钢轨1阶垂向弯曲的峰值频率较刚性道床轨道低，这是由于低频的钢轨振动主要受轨道垂向刚度影响，在轨枕下方加入轨下弹性垫层将降低轨道垂向的总刚度值，使得钢轨的1 阶弯曲变形频率向低频移动，幅值减小；频率为270 Hz 的峰值则是由轨枕相对于钢轨的反相振动引起的，如图9（b）所示，这是因为在轨枕下加入轨下弹性垫层增加了轨道的垂向自由度，在对应频率的简谐单位力激励下被激发出来。

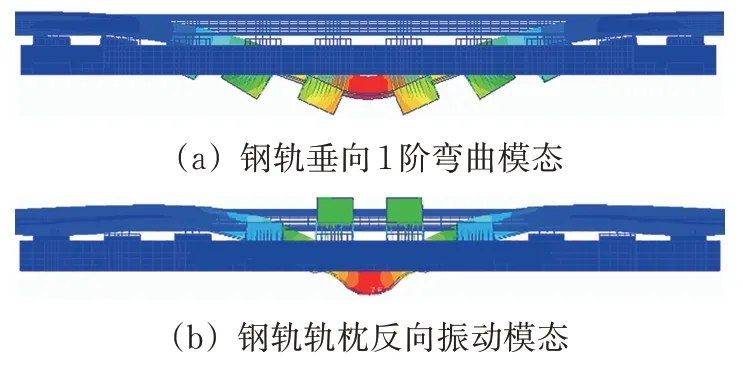
图9 弹性短轨枕轨道振型模态

弹性短轨枕轨道轨下结构的振动响应如图10所示。由图10可知：轨枕和道床板在124，270 和1 460 Hz频率位置均出现了振动峰，由轨道模态可知，124 和270 Hz 处的振动峰分别由钢轨的1 阶垂向弯曲振动和钢轨轨枕间的反向振动模态引起，而1 460 Hz处的振动峰则是由在简谐激励力作用下轨枕结构的1阶垂向弯曲振动模态激发。

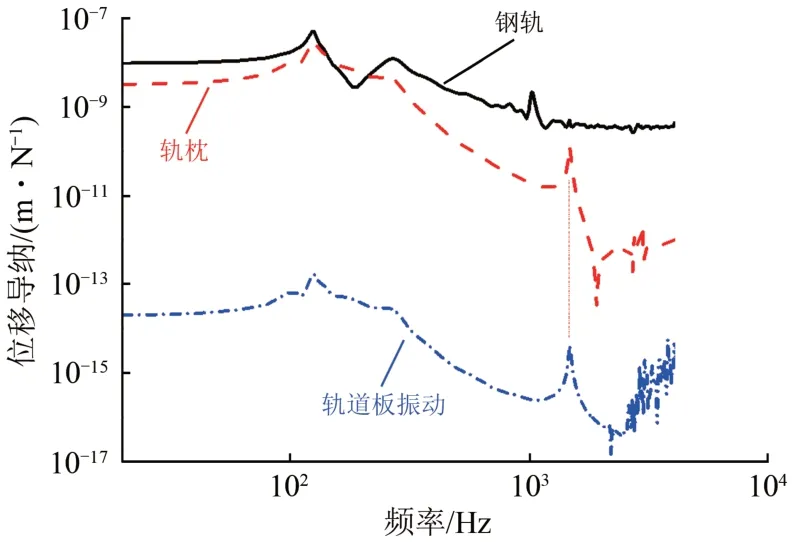
图10 弹性短轨枕轨道各结构的位移导纳

图11给出了2 种轨道垂向振动的传递情况。由图11可知：相对于弹性短轨枕轨道，刚性道床轨道的道床板垂向振动位移高出将近2 个数量级，而2 种轨道的钢轨垂向振动差异较小，这表明弹性短轨枕轨道良好的垂向振动衰减能力。

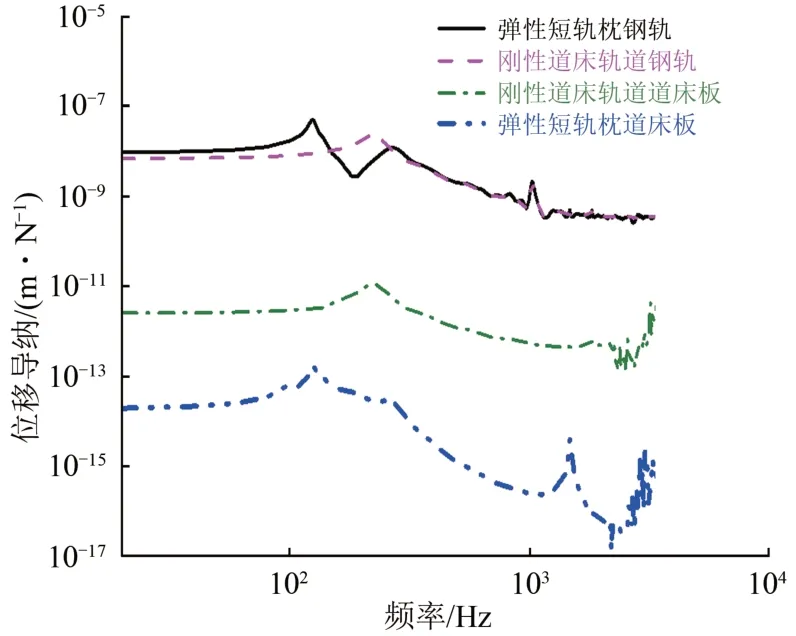
图11 弹性短轨枕轨道和刚性道床轨道的位移导纳

为了更直接地对比2种轨道的减振性能，图12给出了2 种轨道的隔振效率对比图。由图12可知：弹性短轨枕轨道的隔振效率在整个研究的频率范围内均高于刚性道床轨道，弹性短轨枕轨道的隔振效率均保持在1.000 0，表明弹性短轨枕轨道具有较好地隔振性能，并且隔振能力几乎不会受到外激励频率的影响；相对弹性短轨枕轨道，刚性道床轨道隔振效率则要小，最大的隔振效率出现在0～140 Hz 的频率范围，为0.999 6，同时轨道的隔振效率会随着外激励频率有较大变化，当外激励频率增加时，刚性道床轨道的隔振效率有降低的趋势，但是在高频有较大的激增波动，在频率为1 020 Hz位置处，刚性道床轨道的隔振效率突然增大为0.998 0，此频率对应的是钢轨的垂向Pinned-Pinned 振动，表明钢轨的Pinned-Pinned振动的垂向传递较差。

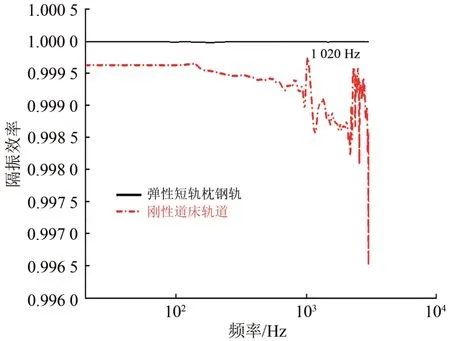
图12 弹性短轨枕轨道和刚性道床板轨道隔振效率对比

可见，于刚性道床轨道相比，弹性短轨枕轨道具有较为优良的隔振性能。

2.2 弹性短轨枕轨道声辐射特性

采用直接边界元法计算弹性短轨枕轨道的声辐射［4］。对于三维振动体的外部声辐射问题，边界单位法向量指向单元外部，当x点位于区域边界上时，Helmholz积分方程为

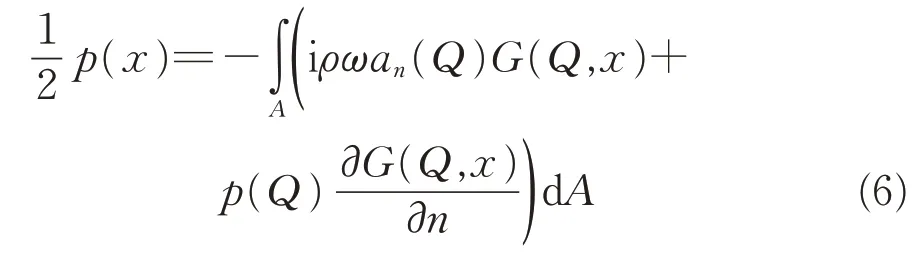
式中：p（x）为边界点声压；ρ为空气密度；an（Q）为边界区域任意点Q的法向加速度；G（Q，x）为自由空间的格林函数；A为边界区域面积。

对边界积分方程进行离散，可得边界元求解方程

式中：H和L均为系数矩阵；p为表面点的压力矩阵；an为模型表面点法向方向的速度矩阵。

本文通过指定模型表面上的节点法向速度（Neumann边界条件）求解模型表面上的声压。

根据所求得的结构表面各点的声压，并通过结构的振动响应求得结构表面的法向速度，进而可求得轨道结构的辐射声功率Wrad为

对于轨道声辐射研究，进行轨道钢轨和轨下结构声辐射贡献量分析对于噪声的控制具有较大的价值。对声功率级进行A 计权，从而能够更好地模拟人耳对于声音的感受程度。

基于声学边界元理论，在轨道有限元结构的表面进行单元划分就可以得到所需要的声学网格，基于上述边界元理论可求得轨道结构的辐射声功率，轨道结构的声学网格模型如图13所示。

图13 轨道结构的声学网格模型

图14给出了单位垂向简谐激励力下的轨道整体和轨道各结构A 计权的声功率级。计算频率范围为0～3 500 Hz，在轨道的垂向振动声辐射分析中，在频率低于240 Hz 时道床板和轨枕较钢轨对噪声的贡献量大，随着外激励频率增加，轨下结构总的贡献量下降幅度较大，钢轨此时成为主要的噪声输出源。从钢轨的声功率曲线能够看出：在1 020 Hz 频率位置出现了声功率的极值，这是由钢轨的Pinned-Pinned 振动引起的；轨下结构在1 460 Hz处也出现了声功率级的峰值，这是由轨枕在激励力下产生的1阶垂向弯曲振动所致，模态振型如图15所示。

由轨道各结构的声功率级曲线可知：对轨道进行噪声控制时，在低频时控制钢轨下结构的振动声辐射，而在高于240 Hz 的频率时，主要对钢轨采取相应的降噪措施以降低轨道整体的振动声辐射。

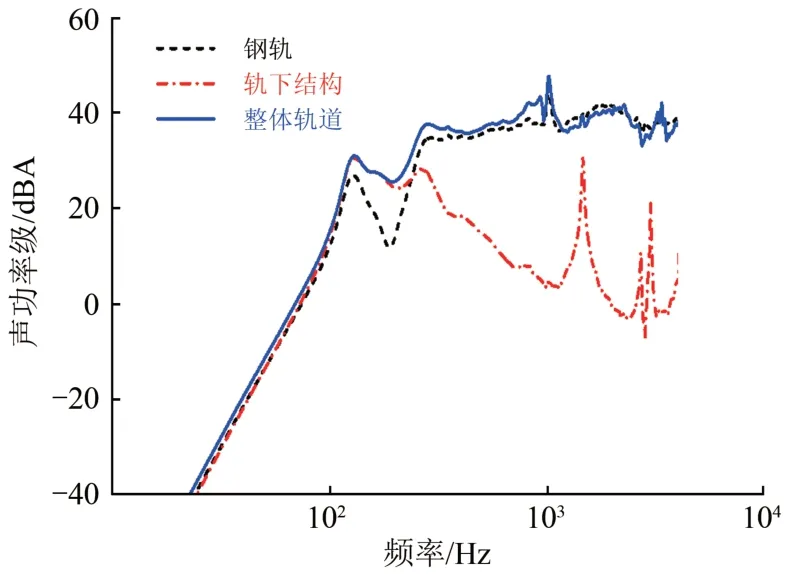
图14 轨道各结构声功率级（A计权）

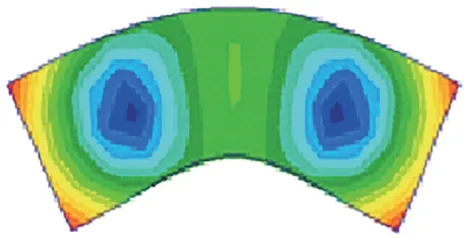
图15 轨枕垂向1阶弯曲模态

2.3 轨下支承刚度对其声振特性的影响

通过上述的分析可得，相对于刚性道床轨道，弹性短轨枕轨道在轨枕下加入了轨下弹性垫层大大提升了轨道的垂向减振性能，那么分析轨下弹性垫层刚度对于轨道声振特性的影响就显得尤为重要。因此下文对不同轨枕支承刚度下的轨道振动和声辐射特性进行分析。

轨枕下支承刚度需要根据实际列车运行情况选取合理的参数。对轨枕下支承刚度分别为40，160和200 MN·m-1时的弹性短轨枕轨道振动和声辐射特性进行分析。

图16给出了不同轨枕支承刚度下钢轨和轨下结构的垂向位移导纳。由图16可知：轨枕支承刚度主要影响400 Hz 以下的钢轨振动，即刚度控制区；当轨枕下刚度为40 MN·m-1时，轨道的垂向刚度较低，钢轨在外激励作用下振动幅度较大，即能量更多地停留在钢轨和轨枕结构上，道床板的振动较小，此时弹性短轨枕轨道减振性能较好，但是较大的钢轨振动位移使得轨道的稳定性较差；随着轨枕下支承刚度增加，轨枕与道床板间的耦合作用增加，钢轨上的振动能量更多地传递到轨枕下结构，振动能量衰减效果较好，因此加大轨枕下刚度能提升钢轨的垂向稳定性；由于钢轨的振动能量更多地传递到轨下结构，道床板的垂向振动位移也随之增加，轨道的减振性能降低。因此轨枕下垫板垂向刚度的选取需要在保证钢轨稳定性的同时兼顾轨道的减振性能。

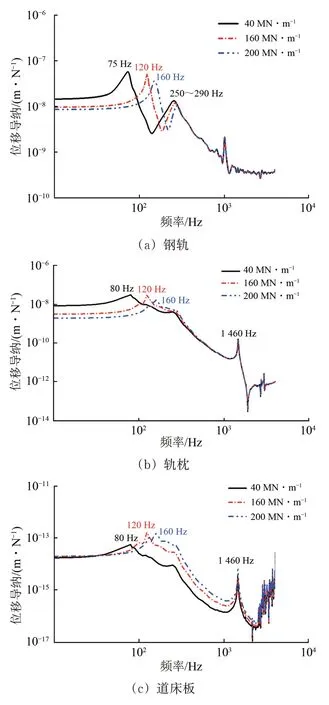
图16 轨道垂向振动位移导纳

对轨道的各部分在不同轨枕支承刚度下的总声功率进行分析，结果见表1。

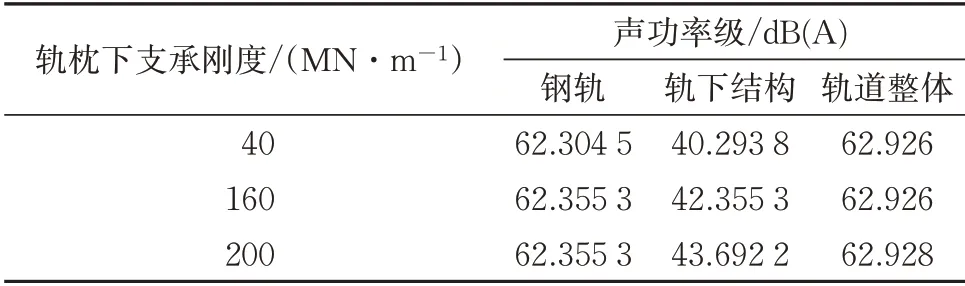
表1 轨道各结构声功率级

对轨道整体结构进行总声功率级分析可知：在0～3 500 Hz 频带范围内钢轨的总声功率级高于轨下结构的总声功率级，为轨道整体结构声辐射的主要贡献源；随着轨枕下支承刚度增加，钢轨在0～3 500 Hz的声功率级有微幅增加，从62.304 5 dB（A）增加到62.355 3 dB（A），这是由于随着轨枕下刚度增加钢轨1阶垂向弯曲峰向高频移动，同时钢轨的声辐射效率随着频率增加而增加，因此钢轨在1阶垂向弯曲振动模态下会辐射出更多的噪声；轨枕下支承刚度增加使得振动能量更多地传到轨下结构上，导致轨下结构总声功率级增大；当轨枕下支承刚度从40 MN·m-1增加到200 MN·m-1时，轨下结构的总声功率级增加约3 dB（A）；随着轨枕下支承刚度的增加，轨道整体的总声功率级有微幅增高，从62.926 dB（A）升高到62.928 dB（A），表明降低轨枕支承刚度对降低轨道整体的噪声辐射作用小。

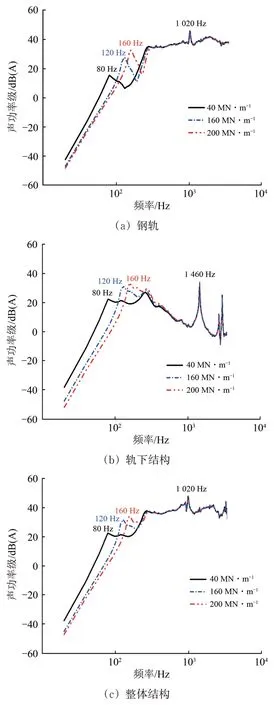
图17 弹性短轨枕轨道辐射声功率

图17给出了钢轨、轨下结构和轨道整体结构的声功率级。由图17可见：轨枕下支承刚度的改变也仅对结构低频位置的声功率级产生影响，当轨枕下刚度改变时，轨下结构的辐射声功率受到刚度改变影响较大，对应于轨道1阶弯曲振动位置的声功率级受轨枕下支承刚度影响较大，因此在增加轨枕下刚度时轨下结构声功率级增加较大；对于钢轨而言，由于钢轨显著的声功率峰值出现在较高的频率段，轨枕下支承刚度的改变对整体的声辐射影响也就相对较小，因此对于钢轨在0～3 500 Hz 的频段内的声功率级影响就较小。

通过振动分析可知：随着轨枕下支承刚度增加，钢轨的振动向轨下结构传递效率加大，使得钢轨振动减小，然而轨下结构振动加剧降低了轨道的减振性能。从轨道声辐射来看，随着枕下支承刚度增加钢轨的垂向弯曲振动峰向高频移动，而随着频率增加钢轨的辐射效率增加，最终也将导致钢轨的声功率级增加。从轨道的整体结构声功率级来看，降低轨枕下支承刚度能够降低轨道整体结构的声功率级，因此轨下刚度需要选取适中的参数同时保证良好的减振和降噪性能。