弹射冲击荷载下重载铁路路基动应力特征

（西南交通大学 土木工程学院，四川 成都 610031）

铁路“十三五”发展规划强调我国在铁路领域应积极推动军民融合深度发展，推进国防与铁路互联建设［1］。其中，重载铁路作为军事用途的重要基础设施，将重载铁路作为导弹发射场坪极大地提高了发射的随机性、机动性和隐蔽性［2-4］。

在民用重载铁路方面，众多学者采用理论分析、试验研究及数值模拟等手段针对列车振动荷载作用下重载轨道路基系统的动响应展开了分析。蔡德钩等［5］分别通过传统极限平衡法和强度折减法探讨了列车轴重、路基高度和抗剪强度指标等因素对重载铁路路基边坡稳定性的影响；冷伍明等［6］通过动三轴试验探讨了在列车往复荷载作用下重载铁路路基粗粒土填料的变形和强度特性；Mei 等［7］通过建立重载铁路车辆—轨道—路基三维动力有限元模型分析了轨道高低不平顺对路基面动应力分布的影响，并采用柯尔莫哥洛夫检验方法对动应力峰值的随机分布特征进行了研究；常卫华［8］、张栋［9］、孙东泽［10］等通过有限元软件建立重载铁路轨道路基系统动力模型，分析了不同列车轴重下轨道路基系统的动响应特征。

与普通列车振动荷载相比较而言，导弹弹射时引起的冲击荷载具有以下3 方面的特点：其一，弹射荷载的幅值较大，约为普通列车荷载幅值的2～4 倍，因而弹射荷载下的动响应影响深度更深，对路基动强度的要求更高［11］；其二，普通列车振动荷载通常采用简谐荷载［12-13］、准静态荷载［10，14］和轮轨冲击力［15-17］进行模拟，而弹射荷载则是采用单周期梯形脉冲荷载进行模拟［4，18-19］，使得弹射荷载下轨道路基动响应的时域谱和频率谱与普通列车荷载相比有较大不同；其三，弹射荷载作用模式为定点加载，因而在定点加载过程中路基岩土体并不会产生主应力轴旋转（移动效应）［20］现象。针对弹射荷载的以上特点，对军用重载铁路路基的沉降控制、填筑材料选取、压实标准以及路基病害防治等方面提出了更高的要求。目前关于弹射荷载作用下重载铁路路基动响应特征的研究鲜有提及。

本文采用梯形脉冲荷载模拟弹射冲击，利用高度非线性显式动力分析程序ANSYS/LS-DYNA3D建立轨道—路基—地基系统三维动力有限元模型，并引入三维一致黏弹性人工边界及其等效边界单元，对比分析重载铁路路基系统在不同幅值弹射荷载作用下的动响应特征，并提出不同幅值的弹射荷载作用时路基填料地基系数K30的建议取值。通过Boussinesq 弹性理论和我国林绣贤多层系统当量理论验证有限元模型的可靠性。长度取72 m，地基横向宽度取30 m，地基深度取5 m。最终建立的重载铁路轨道—路基—地基三维相互作用动力模型如图1所示。

1 三维显式动力分析模型

利用高度非线性显式动力分析程序ANSYS/LS-DYNA3D 分析弹射冲击作用下重载铁路路基振动响应特征及其变化规律。

根据圣维南原理，在网格划分时对求解区域进行网格加密。模型中的弹条Ⅲ型扣件采用具有3向刚度和阻尼的显式离散梁单元BEAM161 模拟，其垂向（Y向）弹簧刚度系数取7.5×107N ⋅m-1，垂向黏滞阻尼系数取4.8×104N ⋅s⋅m-1；轨道、路基结构和地基均采用适应性较强的空间8 节点6面体显式实体单元SOLID164离散。有限元模型共划分1 133 616 个单元，1 227 019 个节点。计算的实际时步长为4.5 μs，在计算时间内共划分了222 221个时步数。为提高计算精度，分析中时步因子取0.9，质量缩放比例取-5 μs。有限元模型的纵向

图1 轨道—路基—地基三维显式动力分析模型（单位：m）

钢轨和轨枕采用各向同性线弹性材料模型模拟；将路基岩土体视为无损材料并考虑到岩土体的受压屈服远大于受拉屈服，道床、路基和地基的材料特性选用程序内置的Drucker-Prager 弹塑性本构模型模拟。该模型仅考虑3个计算参数，即黏聚力、内摩擦角和剪胀角。在非关联流动法则下，为防止程序在计算过程中产生负体积异常，剪胀角取0°［21］。模型采用的结构尺寸和材料计算参数参考TB 10625—2017《重载铁路设计规范》［22］（简称《规范》）。模型的计算参数见表1。

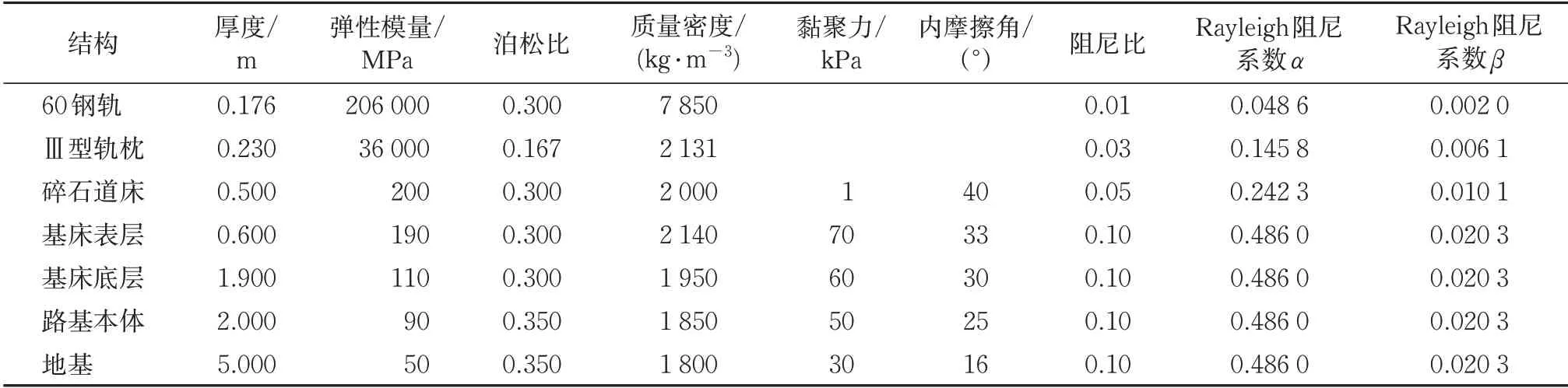
表1 结构几何参数和材料本构参数

钢轨、轨枕、道床、路基和地基岩土材料的阻尼比参照经验取值，结合材料阻尼比和模态分析得到的轨道—路基—地基系统固有频率换算出Rayleigh阻尼系数α，β。模态分析中采用Block Lanczos 法提取前10阶固有振型，其中第1阶和第2 阶振型相对应的自振频率分别为4.167 4和5.357 7 Hz。

由于用梁单元模拟的扣件仅起到垂向约束钢轨的作用，故还需对钢轨的横向（X向）和纵向（Z向）位移施以固定约束；为模拟无限地基的辐射阻尼和弹性恢复性能，在LS-DYNA3D 程序中成功引入计算精度和鲁棒性良好的三维一致黏弹性人工边界及其等效边界单元［23-26］，并将边界单元的最外层节点固定。模型中共设置13 个边界单元，如图2所示。

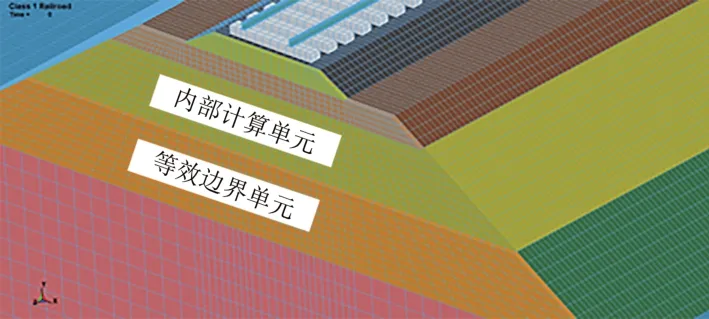
图2 三维一致黏弹性人工边界单元

边界单元的等效剪切模量和等效弹性模量采用下式确定［23-26］。

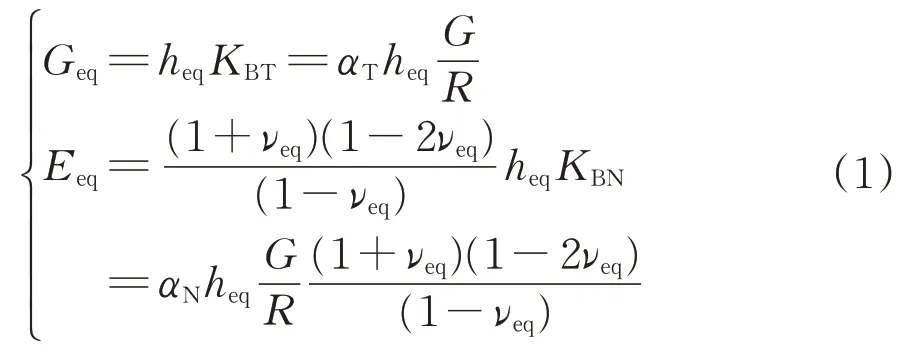
式中：Geq和Eeq分别为等效剪切模量和等效弹性模量；KBT和KBN分别为人工边界弹簧切向和法向刚度；νeq为等效泊松比，本文统一取0；G为介质剪切模量；heq为边界单元厚度，本文统一取0.14 m；R为加载点中心至人工边界面的平均距离；αT和αN分别为切向与法向黏弹性人工边界修正系数，采用推荐值0.67和1.33。

由于本文边界单元采用各向同性线弹性材料模拟，故边界单元的等效阻尼系数取3个方向系数的平均值，即

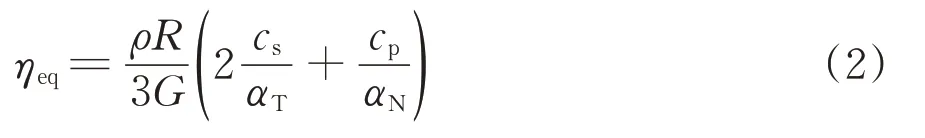
式中：ηeq为等效阻尼系数；cs和cp分别为介质S 波和P波波速；ρ为介质质量密度。

由于模型各结构层材料计算参数不同，故相应位置的边界单元材料参数也不同。由式（1）和式（2）计算得到的边界单元材料参数见表2。

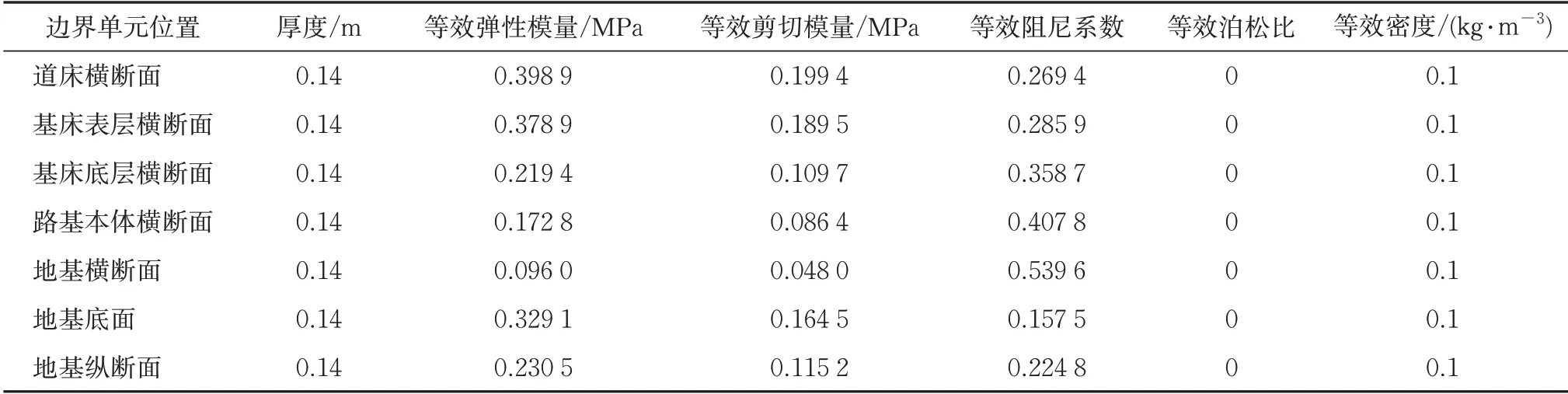
表2 等效边界单元材料本构参数

2 弹射冲击荷载的模拟

弹射冲击荷载采用梯形脉冲荷载模拟。为分析重载路基动应力响应在不同幅值弹射荷载作用下的变化特征，同时考虑到弹射荷载幅值的不确定性，选取幅值为150，200，300，400，500 和600 kN的6 种工况荷载进行研究。图3为不同工况荷载的时程曲线，由冲击荷载时域波形可知，梯形脉冲是在三角形脉冲的基础上考虑了荷载峰值的延续性，荷载持续作用的时间为1.0 s，在0—0.25 s 时段荷载线性增长至脉冲幅值，此阶段为加荷阶段；在0.25—0.75 s时段荷载保持恒定，此阶段为稳定阶段；在0.75—1.0 s 时段荷载线性衰减至0 kN，此阶段为卸荷阶段。这3个阶段的振动类型为受迫振动，卸荷后的阶段为自由振动。下文仅针对受迫振动阶段的动响应进行研究。

数值计算中为简单模拟导弹弹射的过程，可将弹射荷载等效为6组集中荷载（轮对荷载）并定点施加于钢轨轨面中心的节点上，且每个集中荷载的幅值相等。文献［27］针对特种荷载沿纵向的最不利作用位置进行了探讨，认为最外侧轮载力位于轨枕正上方时为轮群荷载的最不利作用位置。基于此结论，将最外侧集中荷载作用于轨枕正上方，荷载间距依次为1.4，1.6，2.2，1.6和1.4 m，荷载布置如图4所示。

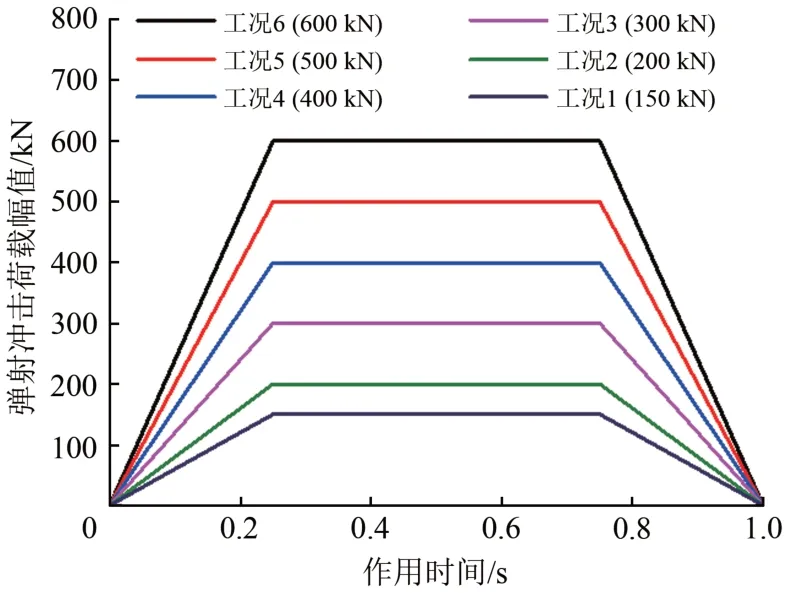
图3 不同工况时弹射荷载的时程曲线

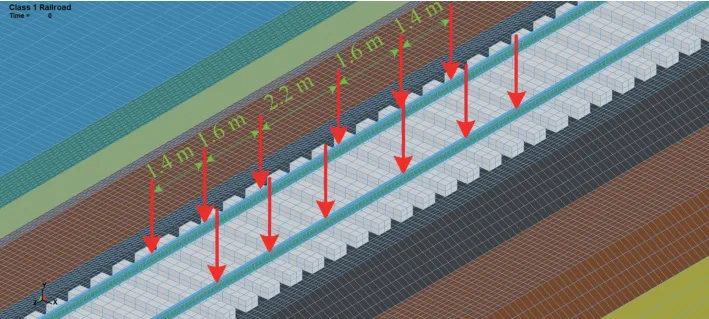
图4 弹射荷载作用示意图

3 模型可靠性理论验证

目前关于弹射荷载作用下重载铁路路基实测动应力响应的数据较为匮乏，因此仅通过理论计算结果验证数值模型的准确性。根据Boussinesq 弹性理论和我国林绣贤多层系统当量理论［28］编制计算程序计算150 kN 单轮载作用下路基不同深度处的竖向附加动应力，计算位置如图5所示。根据文献［29］，作用在轨枕正上方的单轮载力由5 根轨枕承担，其分担比值分别为9.24%，24.14%，33.24%，24.14%和9.24%，轨枕底面对动压力的有效支承面积取1.1 m×0.32 m。计算过程应满足角点法条件，理论计算结果和数值计算结果的对比如图6所示。

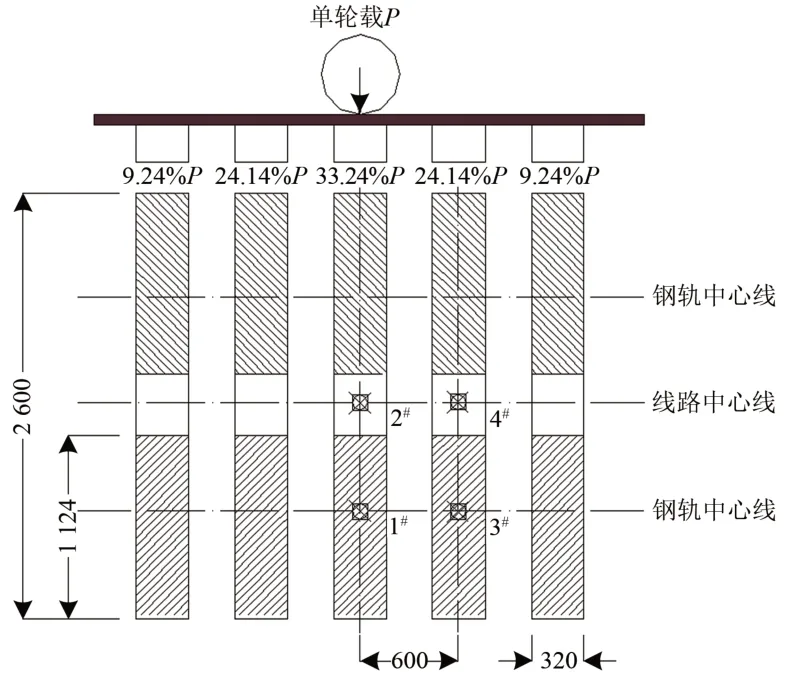
图5 动应力计算位置（单位：mm）

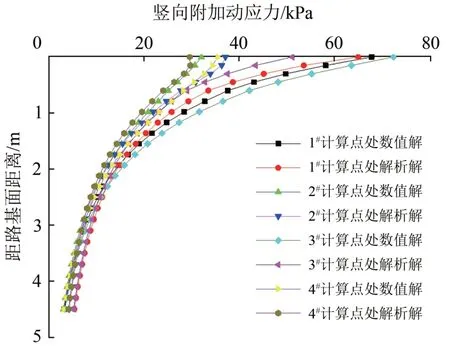
图6 钢轨下方和线路中心处动应力解

由图6可知：在线路中心线处路基面上动应力的理论解出现反弯现象，这是由于计算时假定轨枕中间不承受荷载作用；垂向动应力数值结果和理论结果沿着深度的衰减规律基本一致，但在基床结构层范围内数值解普遍大于理论解，在基床以下数值解小于理论解，应力出现偏差的原因主要是弹性理论假定路基各结构层为均质弹性材料，并未考虑各结构层之间的相互动力作用。通过有限元计算获得的动应力数值结果与理论结果基本吻合，因此，本文建立的轨道—路基—地基动力模型及其参数选取具有一定的合理性。

4 计算结果及分析

4.1 动应力时程特性与空间分布

图7给出了在幅值为150 和600 kN 的弹射荷载作用下路基各结构层顶面垂向动应力的时程分布。由图7可知：各结构层垂向动应力的时程曲线形态与弹射荷载的基本一致，均呈梯形变化，因而路基各结构层动应力的时程变化能反映出弹射荷载的加、卸载状态；路基各结构层动应力与弹射荷载几乎同时在0.25 s 时刻达到最大幅值，也同时在0.75 s时刻开始衰减。

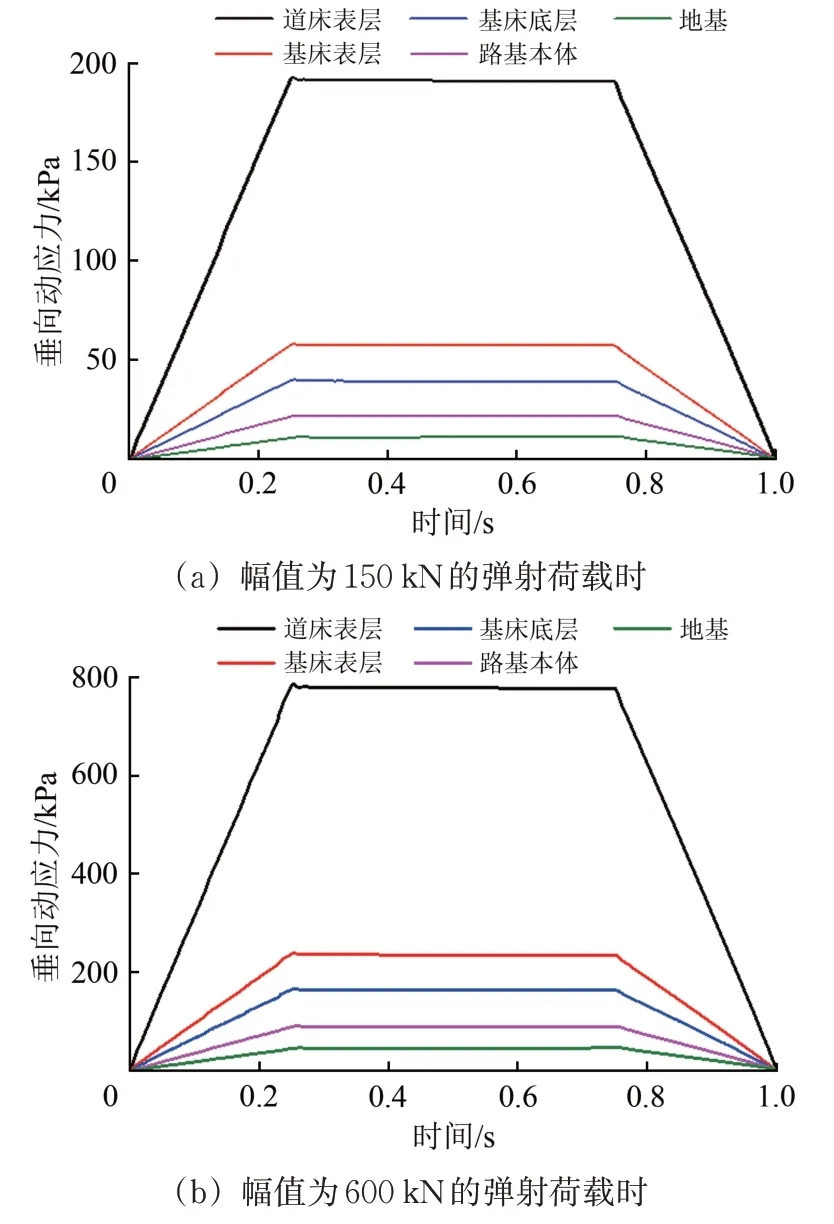
图7 不同弹射荷载作用下路基各结构层顶面垂向动应力时程曲线

图8绘出了600 kN 弹射荷载下道床表层顶面垂向动应力的三维分布。由图8可知：荷载在道床顶面上沿横纵向的影响范围较小；由于轮对效应，道床面动应力的空间分布存在4个关于横纵向对称的波峰，与轮对荷载作用的位置相对应。在轮对中部及荷载影响范围以外的动应力均以数值较小的拉应力为主。

4.2 动应力沿纵向的分布

取距模型起始断面25—45 m 路基横断面作为研究对象，6种荷载工况条件下，钢轨下方路基各结构层顶面垂向动应力沿线路纵向分布如图9所示。

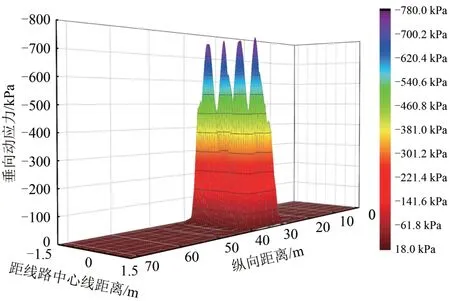
图8 道床表层顶面动应力空间分布

由图9可知：路基各结构层在6 种荷载工况条件下垂向动应力沿线路纵向均呈双峰型对称分布；在6 个轮对冲击荷载的共同作用下，由于叠加效应，各结构层顶面的动应力峰值大致出现在2#和5#轮对下方位置，且在6种不同荷载工况下峰值出现的位置几乎不变。

图10为2#轮对和3#与4#轮对中间处下方路基各结构层顶面垂向动应力随荷载幅值增大的变化曲线。由图10可知：2#轮对和3#与4#轮对中间处下方各结构层动应力随荷载幅值的增大均呈线性增加；2#轮对下方道床、基床表层、基床底层和路基本体动应力的平均增长速率分别为1.113，0.459，0.298 和0.147 kPa ⋅kN-1；3#与4#轮对中间处下方道床、基床表层、基床底层和路基本体动应力的平均增长速率分别为0.355，0.202，0.225 和0.136 kPa ⋅kN-1。可见，对于每个结构层，2#轮对下方位置的动应力随着荷载的增长速率均大于3#与4#轮对中间处下方位置的增长速率。

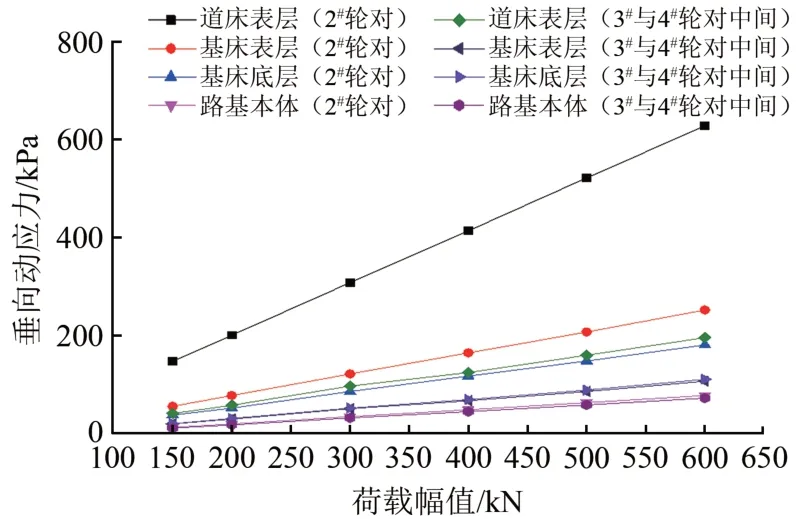
图10 不同位置各结构层动应力与荷载幅值的关系

图11为2#轮对和3#与4#轮对中间处下方各结构层顶面的动应力差值Δσz随荷载幅值增长的变化情况。由图11可知：随着荷载增大，道床、基床表层、基床底层和路基本体在不同位置处的动应力差值分别以0.758，0.257，0.074 和0.008 kPa⋅kN-1的速率呈线性增长。

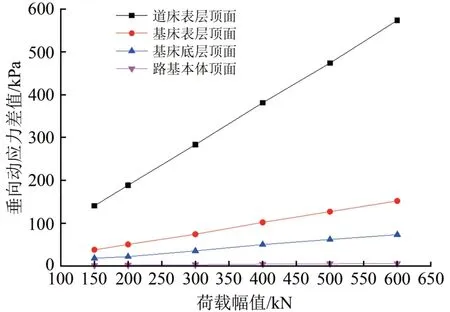
图11 动应力差值与荷载幅值的关系曲线

由以上结合图10与图11的结果分析得知，各结构层顶面的垂向动应力均存在轮对效应。由于路基结构层的分布作用，道床顶面、路基面和基床底层顶面的轮对效应比路基本体顶面的明显。随着荷载幅值增大，道床表层、基床表层及基床底层顶面的轮对效应越来越明显，而路基本体顶面的轮对效应变化不明显。这是因为两边轮对作用的叠加效应受荷载幅值的影响较大，而中间轮对作用的叠加效应受其影响较小。

4.3 动应力沿横向的分布

取距模型起始断面31.7 m 的横断面（三维动力模型沿纵向2#轮对荷载的作用位置）为研究对象，在6种荷载工况下，路基各结构层垂向动应力沿线路横向的分布如图12所示。由图12可知：各结构层在6种荷载工况条件下的垂向动应力沿横向也近似呈对称分布；道床表层顶面和路基面动应力沿横向近似呈“马鞍形”分布，动应力峰值出现在钢轨下方位置；基床底层顶面动应力沿横向的分布更加趋于均匀化，其分布曲线近似“倒盆状”；路基本体顶面动应力呈“钟形”分布，峰值出现在线路中心线下方的位置。荷载幅值对动应力沿横向的分布形态几乎无影响。

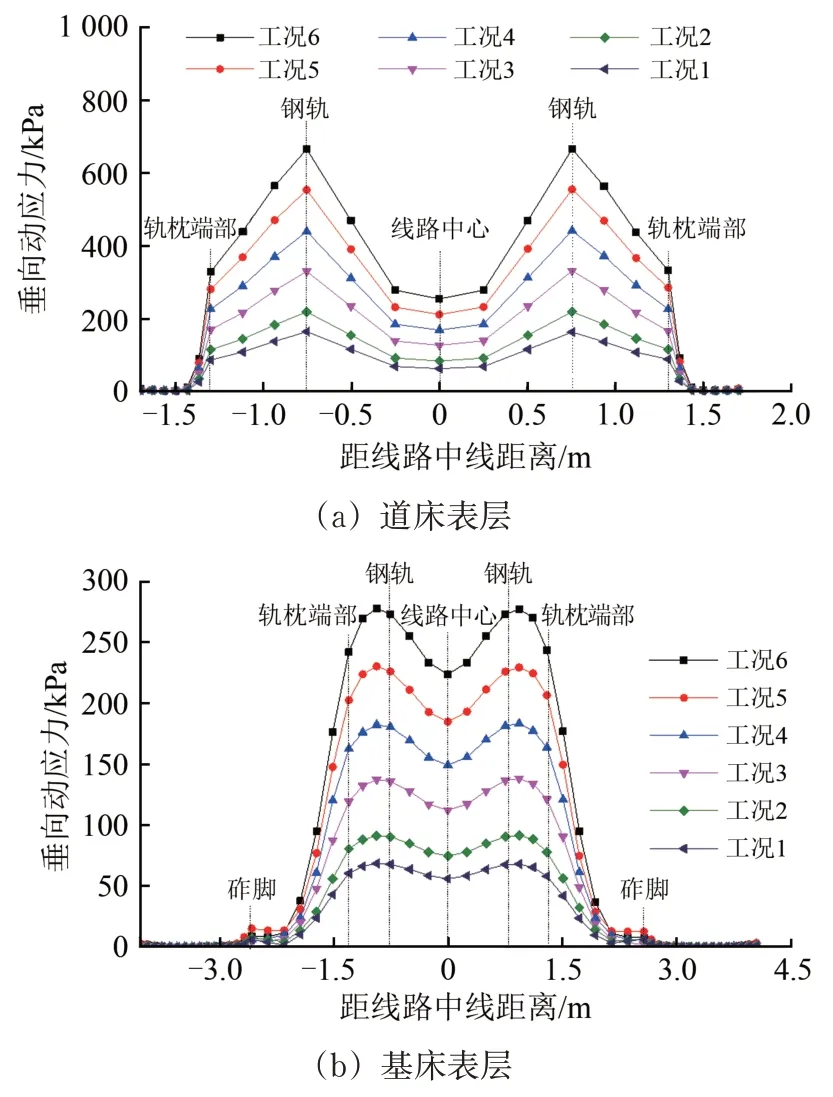
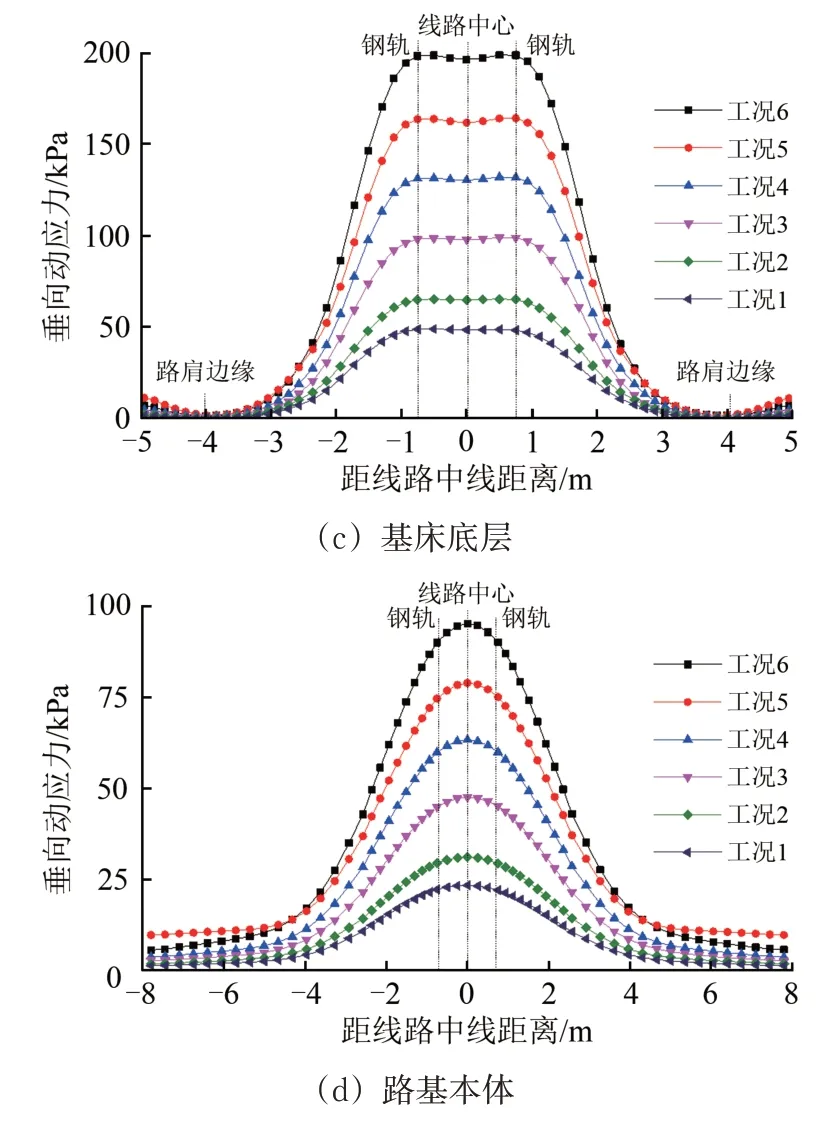
图12 路基各结构层顶面动应力沿横向的分布

由图12（a）可知：钢轨至轨枕端部间动应力衰减速率会随着荷载幅值的增大而加快，600 kN荷载下的衰减速率约为150 kN 荷载时的5 倍，故荷载幅值的增大有利于动应力沿着横向朝外侧衰减。同时，钢轨至轨枕端部间动应力的衰减速率小于轨枕端部至道床边缘间的衰减速率，随着荷载增大，两者差值越来越大；由图12（b）可知，在砟脚附近500 kN 下的动应力要稍大于600 kN 下的动应力；由图12（c）可知，距线路中线4.0 m（路肩边缘）以外基床底层顶面动应力有增大的趋势，产生“翘曲”现象，且增长幅度随着荷载的增大而增大，因此，弹射荷载幅值对路基边坡稳定性有较大影响。

图13给出了钢轨下方和线路中心断面各结构层顶面垂向动应力随荷载幅值增大的变化情况。由图13可知：钢轨下方各结构层动应力均随荷载的增加近似呈线性增大，道床表层的动应力增长最快，其平均增长速率为1.119 kPa ⋅kN-1，基床表层和基床底层次之，其平均增长速率分别为0.471和0.344 kPa ⋅kN-1，2 者的增长速率较为接近，路基本体增长最缓慢，平均增长速率为0.154 kPa ⋅kN-1；线路中心断面各结构层动应力随荷载的增加也近似呈线性增大，道床表层、基床表层与基床底层增长速率均快于路基本体，其平均增长速率分别 为0.428，0.389 和0.344 kPa ⋅kN-1，3 者 的 增长速率较为接近，路基本体增长最缓慢，平均增长速率为0.163 kPa ⋅kN-1；荷载幅值越大，道砟层对钢轨动力的分担作用越明显。

图14给出了钢轨下方和线路中心各结构层顶面的动应力差值随荷载幅值增长的变化曲线。

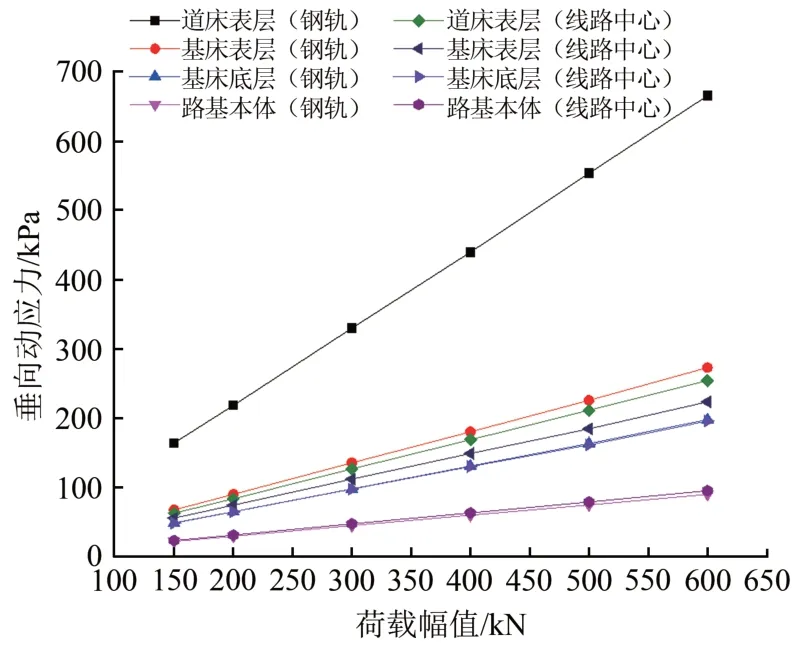
图13 不同位置各结构层动应力与荷载幅值的关系

由图14可知：随着荷载增大，道床顶面和路基面在不同位置处的动应力差值分别以0.691 和0.082 kPa ⋅kN-1的速率呈线性增长，道床动应力差值的增长速率远大于路基面。可见，随着荷载幅值的增加，左右2股钢轨的动力作用越来越显著。

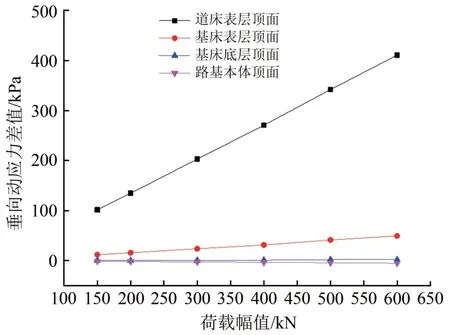
图14 动应力差值与荷载幅值的关系曲线

根据图13和图14可见，不同荷载工况下，基床底层和路基本体在不同位置处（钢轨下方、线路中心、2#轮对及3#与4#轮对中间处下方）的动应力差值均接近于0 且几乎不随荷载的增长而发生变化。因此，随着深度的增加，垂向动应力沿横纵向的分布逐渐趋于均匀化，基床底层和路基本体在不同位置处的动应力差值受荷载幅值的影响非常微小。

4.4 动应力沿垂向的分布

取距模型起始断面31.7 m 的横断面为研究对象，在6种荷载工况下，钢轨投影下方垂向动应力沿深度的分布如图15所示。由图15可知：随着荷载幅值的增大，动应力沿深度方向的衰减规律越趋近于指数型衰减，当荷载幅值为150～200 kN 时，动应力衰减主要发生在道床层和基床表层，距道床面1.1 m 深度以下，动应力衰减为道床面应力的30%以下；当荷载幅值为300～600 kN 时，动应力衰减主要发生在道床层和整个基床层，距道床面3.0 m 深度以下，动应力衰减为道床面应力的14%以下。

道床、基床表层、基床底层和路基本体的平均重度若按19.45 kN ⋅m-3计算，得到如图15所示的自重应力线。在6种荷载工况下，与路基10%自重应力相等的垂向动应力深度均约为距道床层顶面以下8 m，此范围可视为弹射荷载的影响深度。若按照动应力与路基自重应力之比为0.2 的原则确定基床整体厚度，则幅值为150～200 kN 的弹射荷载作用于轨道上时所对应的基床整体厚度约为4 m左右；幅值为300～600 kN 的弹射荷载所对应的基床整体厚度约为5.5 m 左右。所以按照现行规范确定基床整体厚度不适用于弹射冲击作用下重载铁路的基床厚度设计，这一点还有待进一步研究。

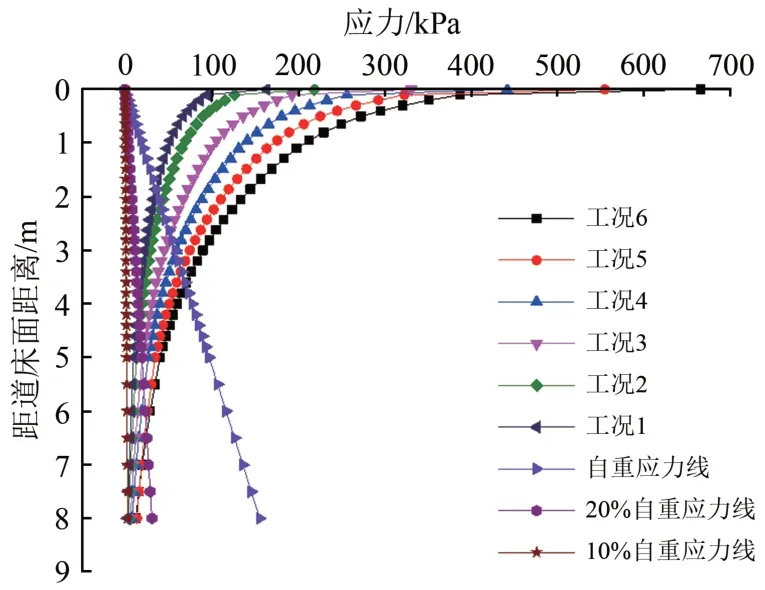
图15 不同荷载工况下垂向动应力沿深度的分布

4.5 动应力峰值与动强度

6 种荷载工况下路基各结构层顶面的动应力峰值见表3。由表3可知：路基各结构层动应力峰值与弹射荷载幅值近似呈线性关系，道床表层动应力峰值随荷载幅值增长最快，其平均增长速率为1.428 kPa ⋅kN-1；基床表层和基床底层动应力峰值的平均增长率分别为0.481 和0.343 kPa ⋅kN-1；路基本体增长最慢，其增长速率为0.163 kPa ⋅kN-1；当荷载幅值从150 kN 增大至600 kN 时，各结构层顶面的动应力峰值的增长幅度基本一致，集中在305%左右。

由表3还可知：当荷载幅值为400 kN 时，道床顶面的动应力峰值达569.3 kPa，此时已不满足重载碎石道床顶面动应力小于允许动强度0.5 MPa的要求［30］。因此，当弹射荷载幅值大于400 kN时，应对既有重载铁路的道床进行充分捣固密实以提高其承载力。

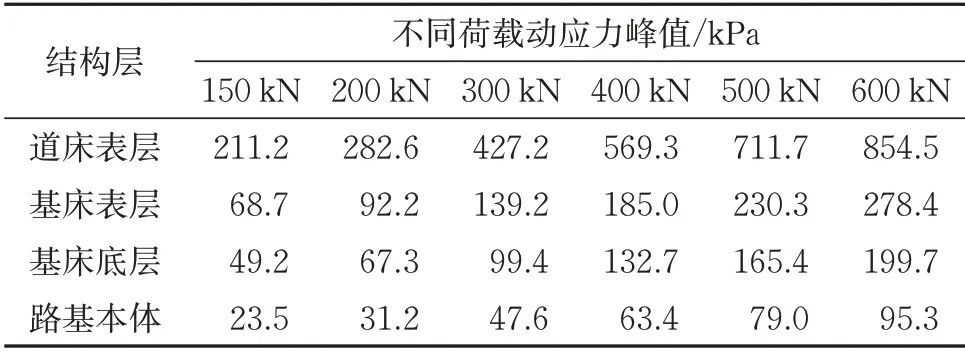
表3 不同荷载工况下路基的动应力峰值

张瑞国、吕文强基于大秦线路基填料地基系数K30的现场测试数据，提出重载铁路路基填料动强度的计算理论。地基系数K30作为路基压实标准的重要控制指标之一，其与路基动强度的关系为

其中，

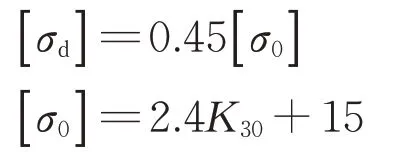
式中：σu为考虑一定安全储备的动强度极限值；[σd]为允许动强度；K为安全系数，本文取1.5；[σ0]为允许静强度。

若基床表层、基床底层和路基本体的填筑材料分别选用A 组填料、碎石类填料和细粒土填料，根据《规范》中关于路基填料地基系数K30的取值范围，并结合式（3）计算得各结构层不同地基系数K30相对应的动强度极限值，见表4-表6。

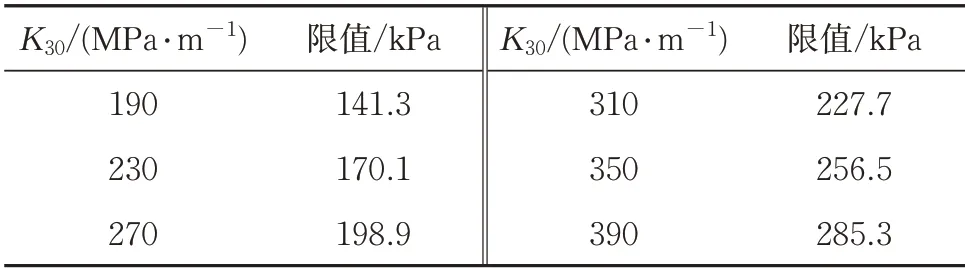
表4 不同地基系数时基床表层动强度限值

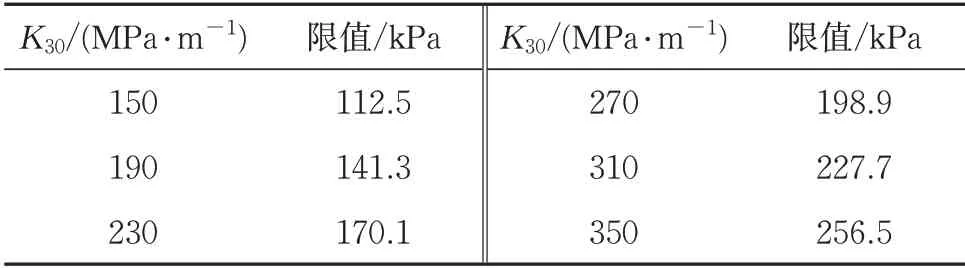
表5 不同地基系数时基床底层动强度限值

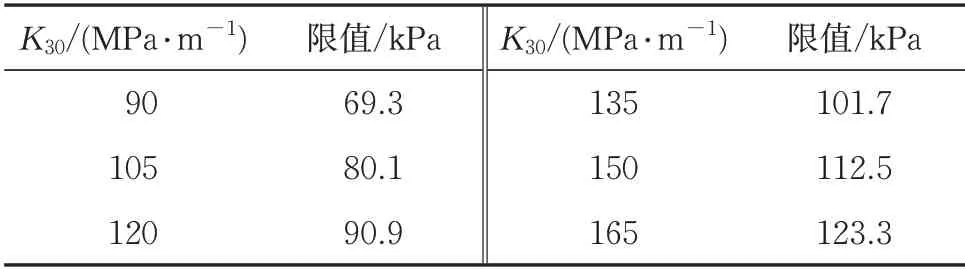
表6 不同地基系数时路基本体动强度限值

结合表3—表6获 得150，200，300，400，500 和600 kN 共6 个弹射荷载幅值下重载铁路路基满足动强度极限值时相对应的地基系数K30的取值，见表7。由表7可知：当荷载幅值为150～300 kN时，基床表层、基床底层和路基本体填料的地基系数K30均取《规范》中的最低限值，即190，150，和90 MPa ⋅m-1；当荷载幅值为600 kN 时，建议基床表层、基床底层和路基本体填料的地基系数K30分别取390，310和135 MPa ⋅m-1。

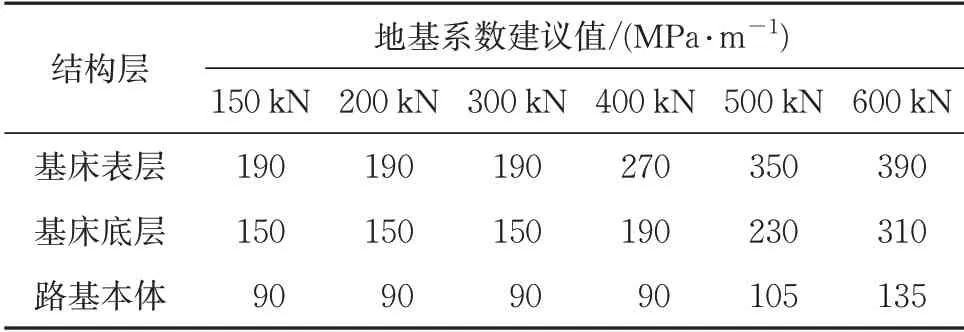
表7 不同荷载工况下地基系数K30的取值

5 结论及建议

（1）路基各结构层顶面垂向动应力的时程曲线形态与弹射荷载的基本一致，均呈梯形变化，且路基各结构层动应力与弹射荷载几乎同时达到相应的最大值也同时开始衰减。

（2）路基各结构层顶面的动应力沿线路纵向均呈双峰型对称分布；随着弹射荷载幅值的增大，道床、基床表层及基床底层顶面动应力的轮对效应越来越明显，而路基本体的轮对效应几乎不受其影响。

（3）道床顶面和路基面动应力沿线路横向呈马鞍形分布，基床底层呈倒盆状分布，路基本体呈钟形分布；随着弹射荷载幅值的增加，左右2 股钢轨的动力作用以及道砟层对钢轨动力的分担作用越来越显著。

（4）随着弹射荷载幅值的增大，路基动应力沿深度方向越趋近于指数型衰减；与路基10%自重应力相对应的弹射荷载影响深度约为道床顶面以下8 m。

（5）路基各结构层顶面处的动应力峰值与弹射荷载幅值均呈线性关系，其中，道床顶面的动应力峰值随荷载幅值增长最快，基床表层与基床底层次之，路基本体增长最慢；为满足弹射荷载下重载路基动强度的要求，当荷载幅值大于400 kN 时，应对既有重载铁路的道床进行充分捣固密实以提高其承载力。若基床表层、基床底层和路基本体的填筑材料分别选用A 组填料、碎石类填料和细粒土填料，则当荷载幅值为150～300 kN 时，建议3 者的地基系数K30分别取《规范》中的最低限值，即190，150 和90 MPa ⋅m-1。当荷载幅值为600 kN时，建议3 者的地基系数K30分别取390，310 和135 MPa ⋅m-1。